Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors

Подождите немного. Документ загружается.

14 High-T

Superconductivity 797

i.e., the temperature dependence of F

is linear in T

and the slope relates to the critical exponent  .Aplot

of F

(T), shown in Fig. 14.45, revealsthat a tempera-

ture independent scaling exponent  cannot account

for the data and therefore confirms the failure of the

3D XY model in external fields of 1 T and above. In

relation with the superconducting transition in non

zero external magnetic fields it has been realized,also

on the basis of the C(T, H) data presented above,that

the reduced anomalies are due to some crossover

phenomenon rather than a true phase transition.

Guided by theoretical insight [157] a distinct phase

transition of firstorder hasthen be identified by high

resolution measurements of thermodynamical prop-

erties, such as the magnetization [158,159] and the

specific heat [160,161], both as a function of tem-

perature in static magnetic fields. Relevant C(T, H)

data [162] is shown in Fig. 14.46. The first order na-

ture of the transitionis confirmed by the observation

of discontinuities in the magnetization at the same

temperatures where the C(T) anomalies occur, re-

questing the release of some latent heat on general

grounds. The transition is believed to be associated

with the ensemble of the vortices of the mixed state.

Transport Below T

(H)

(a) Resistivity

As has already been pointed out above, the zero field

resistive transition is significantly inﬂuencedby ﬂuc-

tuation effects,particularly in those cases where the

anisotropy parameter  is large. It is also interesting

to note that in the temperature range where the in-

plane resistivity 

exhibits the ﬂuctuation induced

paraconductivity, often a substantial increase of the

out of plane resistivity 

is observed [163],i.e., atT

∂

/∂T is negative. An example of this feature, ob-

served for Bi-2212,is shown in Fig. 14.47. Neverthe-

less,evenin these cases,

vanishesin a narrowrange

of temperature,confirming that even for large values

of  , superconductivity is still a 3D phenomenon.

Quite unusual, at least in comparison with com-

mon superconductors, is the inﬂuence of external

magnetic fields on the resistive transition. First we

consider the inﬂuence of external magnetic fields,

oriented along the c-axis, on the in plane charge

transport, i.e., 

(T,H). It may be seen from

Fig. 14.48, where results of measurements [164] of

the in plane resistivity of Bi-2212 are presented, that

an increasing field H does not simply shift the tran-

sition to lower temperatures. Instead, the decrease of



occursin atemperaturerange of increasing width

and from these data it is not a priori clear, where

the resistivity actually vanishes. The extension of the

temperature range of the resistivity drop is partic-

ularly large, if the anisotropy parameter is large, as

in this case. This diagram confirms the above men-

tioned view that a rigorous definition of the upper

critical field H

from resistivity data is difficult. It

turns out that again these features are intimately re-

latedto the behavior of the vortices in themixedstate.

Naturally also 

(T) is strongly affected by external

magnetic fields. In Fig. 14.49 it may be seen that, be-

cause of the magnetic field shifted transition, 

Bi-2212 continues to increase with decreasing tem-

perature, confirming the characteristically different

chargetransport in the two differentcrystallographic

directions [163]. Also here, the subsequent drop of

the resistivity is rather gradual, indicating a cross

over behaviorrather than a distinctphase transition.

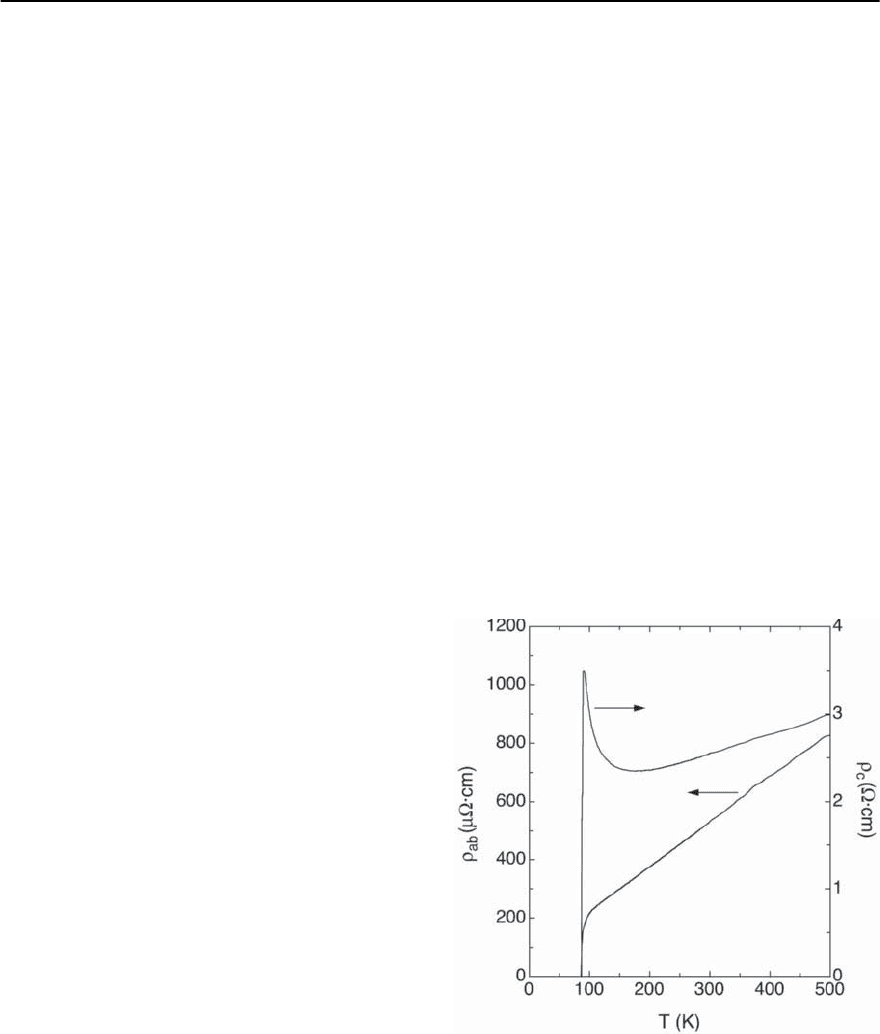
Fig. 14.47. Anisotropy of the temperature dependence of

theelectricalresistivities of single crystallineBi-2212,mea-

sured in theabplane(

)andalongthec-axis (

),respec-

tively. Note the different scales for 

and 

(see [163])

798 H.R.Ott

Fig. 14.48. Magnetic field dependence of the in plane elec-

trical resistivity 

(T) at the superconducting phase tran-

sition of single crystalline Bi-2212. Note the difference in

the features, depending on the orientation of the exter-

nal field. The lower frame emphasizes the low resistance

regime (see [164])

(b) Thermal conductivity

Because of the gap formation in the excitation spec-

trum of electronic quasiparticles of superconduc-

tors, the transport of energy or heat is naturally af-

fected by the phase transition.In common supercon-

ductors,because of the gap formation,the electronic

transport of energy, i.e., the corresponding thermal

conductivity 

, vanishes gradually below T

[165].

Because of the reduced rate of scattering of phonons

with electronic quasiparticles, the lattice contribu-

tion to the thermal conduction is expected [165] and

observed [166] to increase with decreasing temper-

ature below T

, at least as long as no other scatter-

Fig. 14.49. Magnetic field dependence of the out of plane

electrical resistivity 

(T) of single crystalline Bi-2212 (see

[163])

ing mechanisms for phonons dictate their mean free

path. The situation seems to be somewhat different

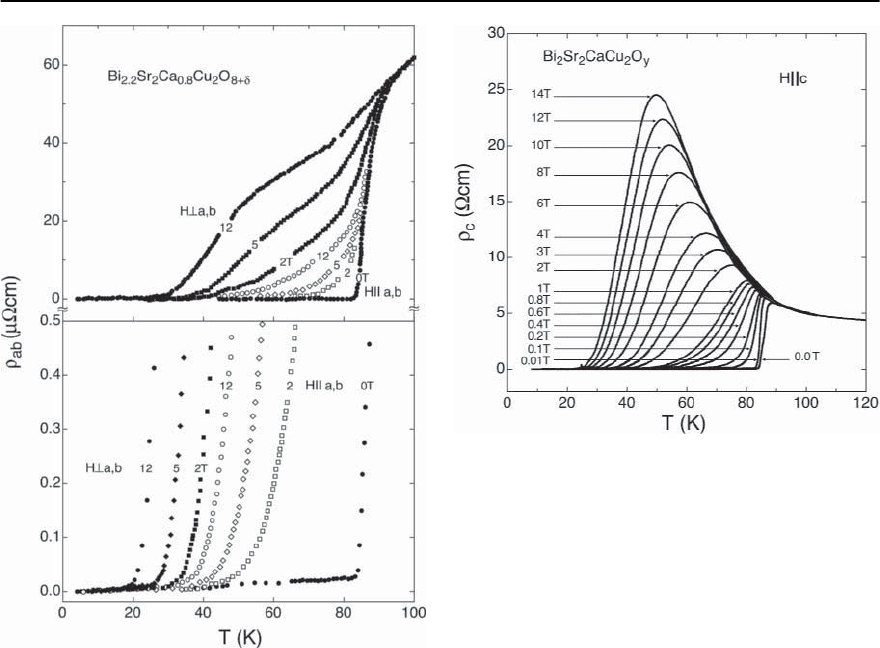
for the cuprate superconductors. In Fig. 14.50 [167]

we show experimental data for the temperature de-

pendence of the thermal conductivity (T) for the

transport of energy parallel to the Cu-O planes of

YBCO-123.Apart from some intrinsic anisotropy be-

tween the a andb direction,themost obvious features

are the discontinuous change of the slope ∂/∂T at T

and the distinct maxima of  at approximately T

/2,

for both crystallographic directions. The anisotropy

ratio of 

/

is constant above T

and the en-

hanced thermal conductivity along the b-direction

is attributed to the additional electronic contribu-

tion due to quasiparticle transport along the Cu-O

chains that are,according to Fig.14.6a, extended only

along the b direction of the crystal lattice. The slight

increase of  with decreasing temperature in the nor-

mal state is interpreted as being due to itinerant lat-

tice excitations. Although at first sight it is tempting

to ascribe the anomalous increase of  below T

an enhanced phonon conductivity, it turns out [168]

that the observed behavior is rather due to an en-

hanced electronic heat conduction, obviously again

a rather unusual phenomenon but, to a certain ex-

14 High-T

Superconductivity 799

Fig. 14.50. Temperature dependences and anisotropy of the

thermal conductivities of single crystalline Y-123, mea-

sured along the a-axis and the b-axis, respectively (see

[167])

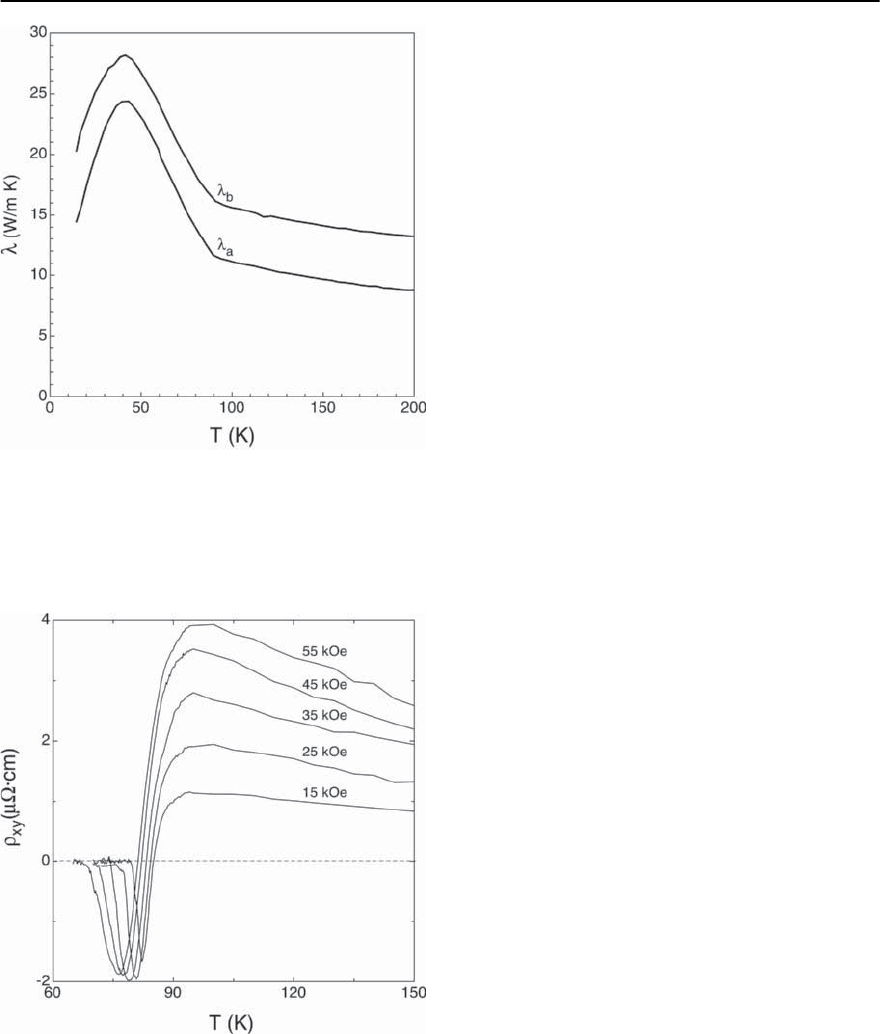
Fig. 14.51. Temperature dependence of the in plane Hall re-

sistivity 

of single crystalline Y-123 in various external

magnetic fields oriented along the c-axis between 60 K and

150 K

tent, also observed in strongly coupled conventional

superconductors [169,170]. For the cuprates it is as-

cribed [168, 171] to an anomalous decrease of the

quasiparticle scattering rate in the superconducting

state which at first was revealed in experiments prob-

ing the surface impedance of cuprate superconduc-

tors below T

[172,173].Assuming that the temper-

ature dependence of the phonon conductivity is not

significantly altered in the superconducting state,the

maxima in  are then a consequence of the compen-

sation of the scattering rate reduction by the reduced

number of quasiparticle excitations because of the

gap formation in the superconducting state.

It turns out that magnetoresistive effects in these

cuprate materials, at least in experimentally achiev-

able magnetic fields, are not really extraordinary.

This isnot quitetrue for the results of measurements

of the Hall resistivity 

. Even for common type II

superconductors,the Hall response in the mixedstate

is somewhat complicated and different model calcu-

lations of what should be expected, lead to different

results[174,175].Thisis even moreso for the cuprate

superconductors where again, some anomalous fea-

tures are particularly well developed. Since the ob-

served anomalous features seem again to be strongly

linked with the properties of the vortex state, we re-

strict ourselves to a brief presentation of the most

important observations. For this purpose we show,

in Fig. 14.51, thetemperature dependence of the Hall

resistivity 

(T) of a single crystal of slightly un-

derdoped YBCO-123 in various external magnetic

fields [176]. Most obvious is the sign change of 

at field dependent temperatures that are close to but

always less than the zero field critical temperature

(0) [177].There is a clear negative shift in temper-

ature where the minimum of 

is observed, with

increasing external magnetic field. At this point it

should be noted that sign changes of 

,although

somewhat less pronounced, have also been observed

in conventional type II superconductors [178]. It is

therefore most likely, that this phenomenon is tied

to the vortex state and its dynamics as such and

not to special intrinsic properties of the cuprate su-

perconductors. Nevertheless, more Although various

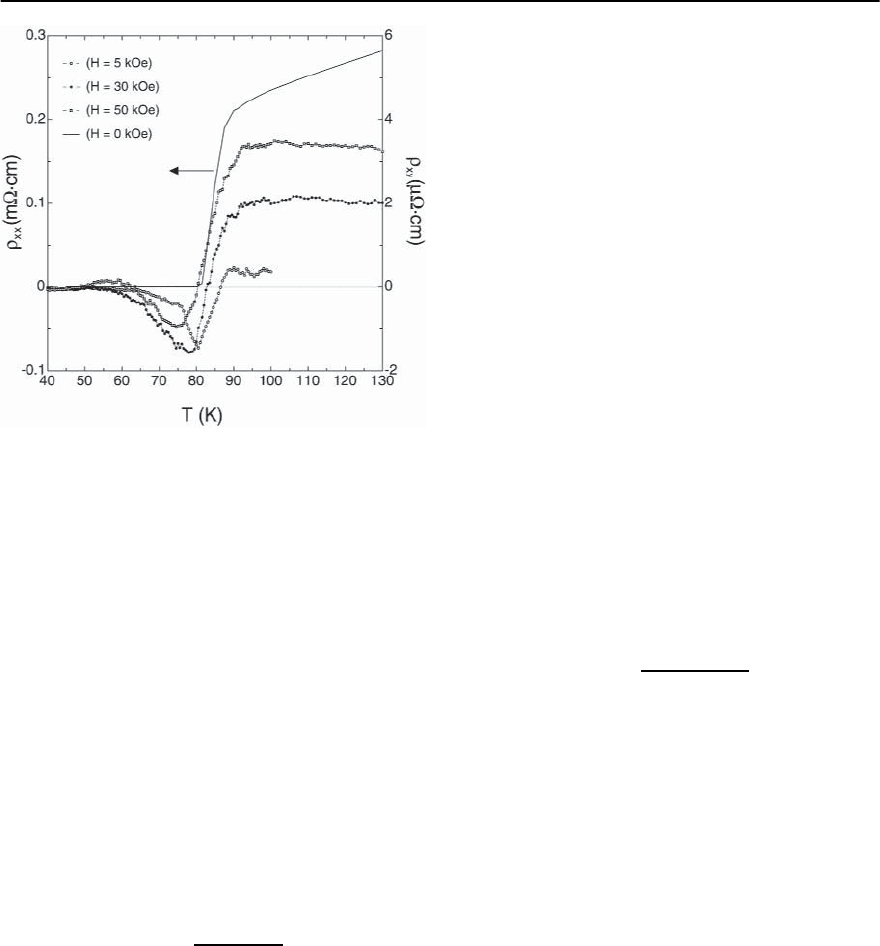
800 H.R.Ott

Fig. 14.52. Temperature dependence of the in plane Hall

resistivity

of single crystalline Bi-2212 in various mag-

netic fields oriented along the c axis between 40 and 130

K. Also shown, as the solid line, is the zero field in plane

electrical resistivity 

explanations for these phenomena have been sug-

gested,itismostlikelythattheHallconductivity

detailed investigations indicate that again the degree

of anisotropy and, in addition, the concentration of

holes introduced by doping, play an important role.

Another set of 

data,obtained from measurements

on a single crystal of Bi-2212material [179],isshown

in Fig. 14.52. The difference to the results shown in

the previous figure is yet another sign change of 

at temperatures much below T

[180].Apartfromthis

observation we note that the deviations from the T

−1

behavior of R

start at temperatures well above the

zero field T

. This seems to indicate that again some

ﬂuctuation effects are significant.





(

+ 

)

(14.19)

is given by the sum of at least two different contri-

butions [181]. One of them is related to the super-

conducting matrix of the mixed state and the sec-

ond would represent the contribution from excited

quasiparticles in the cores of the vortices. There are

obviously different ways for theoretical treatments

of this problem. A number of publications, consid-

ering either the pinning force, ﬂuctuation effects,

a Magnus-type force, two band effects, or charge

imbalances between the vortex cores and the su-

perconducting matrix are available in the literature

[182–187]. A thorough discussion of all of them is

beyond the scope of this review.

Characteristics of the Superconducting State

(Gap Function)

Thestabilityofthesuperconductingstateis,ingen-

eral terms, guaranteed by the formation of a gap

in the quasiparticle excitation spectrum below T

At present we do not consider the very special case

of gapless superconductivity [188], sometimes ob-

served in cases where the quasiparticle mean free

path is much shorter than the coherence length. This

condition is notfulfilled in typical cuprate supercon-

ductors. In the most simple approximation, this gap

is assumed to be isotropic in k space and its mag-

nitude at zero temperature, (0), is a measure for

the free energy difference between the normal and

the superconducting state, the condensation energy

cond

, via [106]

cond

D(E

) · 

(0)

. (14.20)

Since this condensation energy is another manifes-

tation of the Meissner–Ochsenfeld effect, its exper-

imental observation, to be discussed in more detail

below,implies theexistence of thisgapalsoincuprate

superconductors. The opening of this gap at T

also reﬂected in the almost discontinuous enhance-

ment of the specific heat at the critical temperature

of YBCO-123, measured in zero magnetic field.

All these results from measurements of macro-

scopic properties give only indirect evidence for the

presence of a gap and the real way to go are experi-

ments that probe the excitation spectrum of the elec-

tronic quasiparticles directly. Many early tunneling

data revealed the expected loss of excited states in

a narrow energy range around zero energy [189]. A

new way of exploring the occupation of quasiparticle

states near the Fermi energy of superconductorswas

then offered by a significant progress in improving

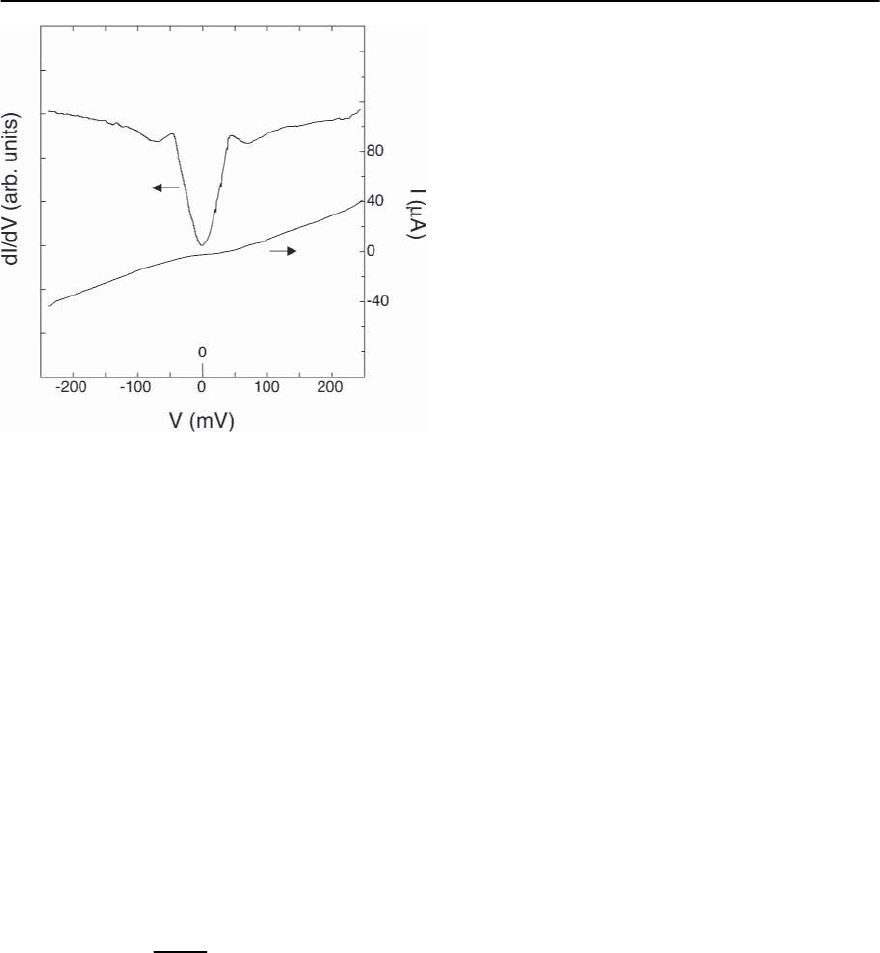
14 High-T

Superconductivity 801

Fig. 14.53. Current and conductance vs. voltage character-

istics of a break junction of a Bi-based copper oxide su-

perconductor, reﬂecting the loss of available states close to

(see [190])

the energy resolution in measurements of photoe-

mission spectra near E

. In Fig. 14.53 we show an

early result of the voltage dependence of the differ-

ential conductivity ∂I/∂V of a break junction of Bi-

based copper oxide, reﬂecting the loss of achievable

states close to E

[190].Beforewe address the issue of

a possible k dependence of the gap function, we con-

sider the informationthat essentially all these exper-

iments provide, the amplitude 

of the gap function

and its temperature dependence. The zero tempera-

ture value 

(0) is of interest because, together with

the magnitude of T

, it reveals the strength of the in-

teraction that provides the superconducting ground

state. In the weak coupling limit, the relevant ratio,

following from the original BCS theory [106] is

2

(0)

=3.56 . (14.21)

Larger values, following from direct experimental

evaluations of T

and 

(T) are usually interpreted

as a manifestation of strong coupling effects.Without

going into details, most of the results of experiments

that are brieﬂy discussed below, indicate ratios of

2

that are factors of 2 to 3 larger than the

value quoted in Eq. (14.21), at least when probing

the superconducting state in the Cu-O planes, i.e., we

are dealing with superconductivity invoking a very

strong coupling.

Although there was,even before these microscopic

experiments were done, never any serious doubt

that the superconducting gap is well established in

cuprate superconductors,therewas,at first,only lim-

ited interest and correspondingly little information

concerning the k dependence (k)ofthegapinmo-

mentum space. The shape or symmetry of (k )is,to

a certain extent at least, tied to the symmetry of the

pairing configuration and the corresponding order

parameter of the superconducting state. Therefore it

isclear thatexperimentalverificationsof theshapeof

(k) are important and useful for the interpretation

of a variety of experimental data, but especially also

for testing predictions of theoretical models. Con-

sidering the overwhelming evidence that supercon-

ductivity in these copper oxides is mainly due to the

special properties of the Cu-O planes and also taking

into account the atomic arrangement of Cu and O in

these planes, it seems suggestive that the most likely

configuration of the gap function (k)hasad

−y

symmetry, also compatible with predictions assum-

ing nonelectron–phonon pairing mechanisms [191].

In the following, a short presentation of various dif-

ferentexperimentalattempts to evaluate(k) and the

corresponding main results that have been achieved,

is given.

Experiments Probing the Gap Anisotropy

The k-dependence of the gap may have trivial causes.

Its anisotropy may be tied to the anisotropy or shape

of the Fermi surface. It is quite conceivable that an

isotropic gap, which essentially relies on the choice

of a k-independent pairing interaction, is not strictly

realized even in conventional superconductors. This

type of anisotropic gaps, based on a pairing inter-

actionwhosestrengthisnotthesameonallparts

of the Fermi surface, may also be present in con-

ventional superconductors and many indirect evi-

dences for this have been accumulated a long time

ago [192].Of much more interest are cases where the

anisotropy of the Fermi surface and of (k)donot

802 H.R.Ott

match. This may best be discussed by invoking the

concept of symmetry breaking at phase transitions,

introduced by Landau [193] and, in more general

terms, by Anderson [194]. For conventional super-

conductors, the formation of a phase-coherent pair

condensate invokes the breaking of the one dimen-

sional global gauge symmetry U(1).A superconduc-

tor is termed unconventional if the corresponding

pair state breaks yet another symmetry, which may,

e.g., be the time reversal symmetry T,thespinro-

tation symmetry R or the translational symmetry X

of the crystal lattice. The resulting symmetry of the

pair state is reﬂected in the symmetry of the order

parameter and also of the gap function. Even if the

symmetry of the gap function or the order param-

eter is known, it is still difficult or even impossible

to conclude rigourously, which kind of interaction

has produced the observed type of symmetry break-

ing.Aspectsof unconventionalsuperconductivity are

also addressed in the chapter on superconductivity

of heavy electron compounds and have extensively

been discussed in [195].

Additional symmetry breaking and correspond-

ing unconventional pairing configurations often lead

to gap functions (k) with nodes, i.e., zero gap am-

plitudes at points or on lines on the Fermi surface.

Such nodes have a significant inﬂuence on the tem-

perature dependence of physical properties that are

dominated by electronic excitations in the super-

conducting state well below T

. For superconductors

with conventional pairing, gap nodes may form only

accidentally and usually the gap assumes non zero

values across the entire Fermi surface. In these cases,

all properties of the superconducting state which

are related with the excitation of electronic quasi-

particles, exhibit an exponential temperature depen-

dence at T/T

<< 1. This is, of course, not the

case if gap nodes are present. Contrary to conven-

tional superconductors for which at zero tempera-

ture the quasiparticle density of states D(E)iszero

between E = E

=0andE = ±,thisisnotso

for many configurations of unconventional pairing.

A well known exception is the superﬂuid B phase of

liquid

He, where an unconventional pair wavefunc-

tion provides a complete non-zero gap [196]. Possi-

ble forms of D(E) close to E = 0 for unconventional

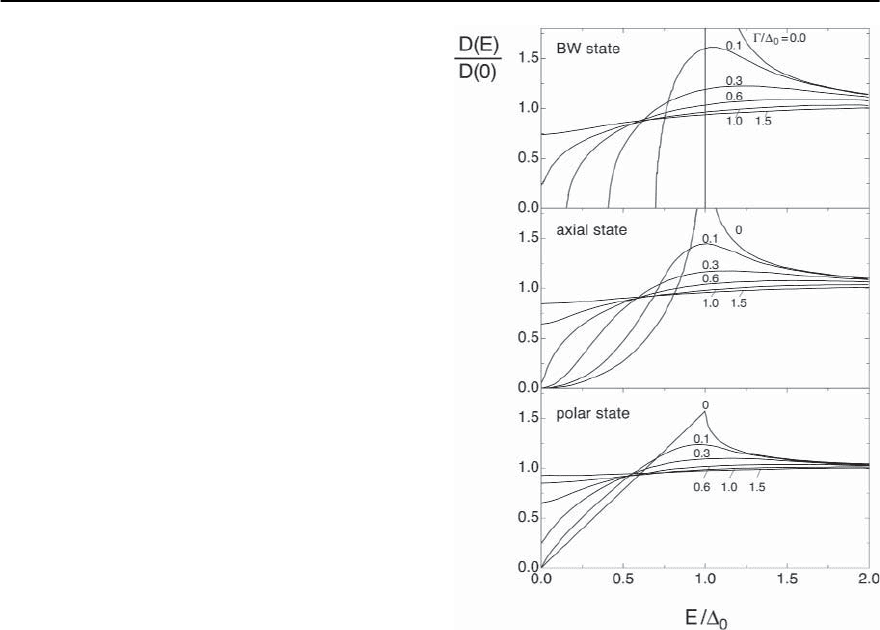
Fig. 14.54. Schematic representation of the energy depen-

dence of the electronic density of states D(E) in the gap

region of unconventional superconductors. The Balian–

Werthamer (BW) state is a nodeless p-wave state. The axial

and the polar state imply point and lines of nodes of the

gap function,respectively.The parameter  /

is a measure

for impurity induced pair breaking (see [195])

pairing states are shown in Fig. 14.54.As may be seen,

D(E) vanishes in powerlaws of E as E → 0.Thenodes

are not always strictly on points or lines on the Fermi

surface. Impurity scattering may widen these regions

where the gap function vanishes. In some cases this

happens even for tiny amounts of impurities or de-

fects, in other cases, a critical value of impurity con-

centration has to be exceeded in order to achieve a

gapless situation.

As an immediate consequence, the above men-

tioned exponential temperature dependence of phys-

ical properties is replaced by power laws in T. As an

example we may quote the electronic specific heat.

14 High-T

Superconductivity 803

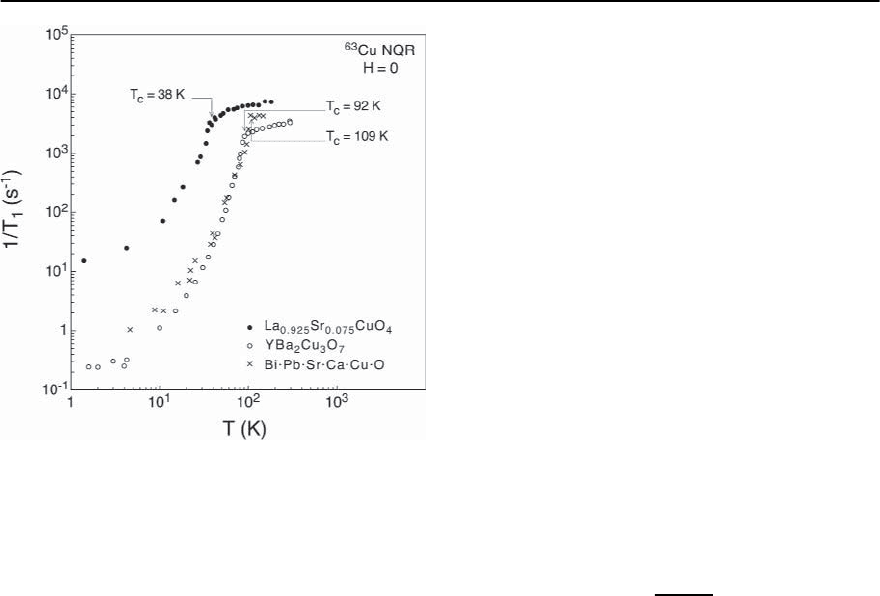
Fig. 14.55. Temperature dependence of the

Cu NQR spin

lattice relaxation rate T

−1

(T) for three different cuprate

superconductors

While for conventional superconductors it is vary-

ing as C(T) ∼exp(-/T), a power law C(T) ∼ T

expected for unconventional superconductors. The

value of the exponent n depends on the configu-

ration of the gap nodes. It is therefore possible to

identify unconventional superconductors by mea-

surements of the temperature variation of selected

physical properties well below T

. Relevant examples

are presented below.

Another feature that is typical for conventional

superconductors but is absent in those of uncon-

ventional varieties, is the observation of coherence

effects that are a consequence of the special configu-

ration of conventional Cooper pairs that are formed

between states with opposite momenta and spins,i.e.,

(k ↑, −k ↓), a major ingredient of the original BCS

theory [106].The observationsof these coherence ef-

fects,which depend on the interactionexerted by the

measuring technique were, at the time, considered

as convincing confirmations for the validity of the

BCS theory [197,198]. Some of the first indications

for unconventional superconductivity in thecuprates

were related with the absence of the coherence ef-

fect that is expected to be observed in measurements

of the temperature dependence of NMR relaxation

rate just below T

[197]. An example for this kind

of data is shown in Fig. 14.55 [199]. The drop of the

relaxation rate T

−1

, measured for Cu nuclear spins,

is abrupt and quite in contrast to the expected rise

of T

−1

with an onset at T

, passing over a distinct

maximum somewhat below the critical temperature

and finally decreasing exponentially at T  T

.This

latter behavior, clearly identified for simple super-

conductors[200],isa typical manifestation of coher-

ence effects.The same set of data,shown inFig.14.55,

has also been claimed to provide evidence foruncon-

ventional superconductivity via the power-law type

temperature dependence of the relaxation rate be-

low T

(a) Penetration Depth

With respect to cuprate superconductors,anearly in-

dication for unconventional superconductivity was

obtained from measurements of the temperature de-

pendence of the penetration depth 

(T) for external

magnetic fields well below T

[201].In simplest terms

this characteristic length is given by



4n

, (14.22)

i.e., it depends on the ratio between the mass m of

the quasiparticles and the density n

of quasiparti-

cles condensed into pairs. The latter is temperature

dependent and reaches its maximum value at T =

0K. As mentioned above, the penetration depth may

be measured using the technique of SR. For high

resolution measurements aiming at establishing the

temperature dependence of the penetration depth at

low temperatures, other experiments seem more ap-

propriate, however. Based on microwave absorption

experiments, which are well suited to measure the

temperature induced variation of 

with respect to

a given value, arbitrarily set to zero, at some chosen

temperature T

,quite reliable valuesof

= 

(T)–



) may be obtained. Corresponding results, ob-

tained for high quality single crystals of YBCO-123at

temperatures above T

=1.3 K [201] (see Fig.14.56),

have demonstrated that 

(

in this case) in-

creases linearly with T, at least between 1.3 and 20

K, i.e., well below T

of about 90 K. This tempera-

ture dependence of 

, is a clear indication that the

804 H.R.Ott

Fig. 14.56. Temperature dependence of the incremental in-

crease of the in-plane penetration depth of single crys-

talline Y-123. The different symbols represent the data for

different samples (see [201])

gap function of YBCO-123 has nodes, most likely on

lines on the Fermi surface. The claim is quite con-

vincing because a control experiment of the same

type, using a sample of a PbSn alloy, a conventional

type II superconductor, resulted in an exponential

increase of 

at temperatures well below T

=7.2

K of this material. Later experiments [202] revealed

that shortening the quasiparticles’ mean free path by

introducing impurities results in 

∼ T

(b) Specific Heat

Since the specific heat C(T) is solely dependent on

the density of states of possible thermally induced

excitations, the temperature dependence of the con-

tribution tothespecific heat due to excited electronic

quasiparticles,C

(T),is bound to reﬂect the presence

of gap nodes. In general, point-type or line-type gap

nodes are expected to result in C

(T)beingpropor-

tional to T

and T

, respectively, at very low temper-

atures at least. Although this verification appears as

being rather trivial in principle, the practical execu-

tion is hampered by the fact, that the subtraction of

not well known background contributionsto C(T)is

less simple as it may seem. Nevertheless, attempts of

this sort have been made, mainly by invoking mea-

Fig. 14.57. Scaling of the low temperature specific heat

of YBa

7−ı

at different temperatures and in varying

magnetic fields (see [206])

surements of the specific heat of close to optimally

doped YBCO-123, both in zero and non-zero mag-

netic fields H. In some work, a T

variation of C

at T  T

and H = 0, indicating line nodes of the

gap [203], was claimed to have been verified [204].

Even more involved is the analysis of specific heat

data obtained in non zero external magnetic fields,

because the structure of the vortices and their nor-

mal cores add to the already present complications.

However, the measured H and T dependencies may

be compared with rigorous theoretical predictions

for the consequences of unconventional gap func-

tions. In particular, line nodes are predicted [205]

to provoke the appearance of a new term represent-

ing the contribution due to the quasiparticle den-

sity of states C

, varying as H

1/2

−1

and replacing

the T

contribution at low temperatures. The pre-

dictions for line nodes include a crossover behavior

at a critical value z

= H

−1/2

to a high-T,low-

H regime with two separate contributions, an H in-

dependent T

term and a temperature independent

contribution varying linearly with H.Bothpredic-

tions have been verified experimentally [204, 206].

One of the verifications of the predicted scaling

of C

in the low temperature regime is shown in

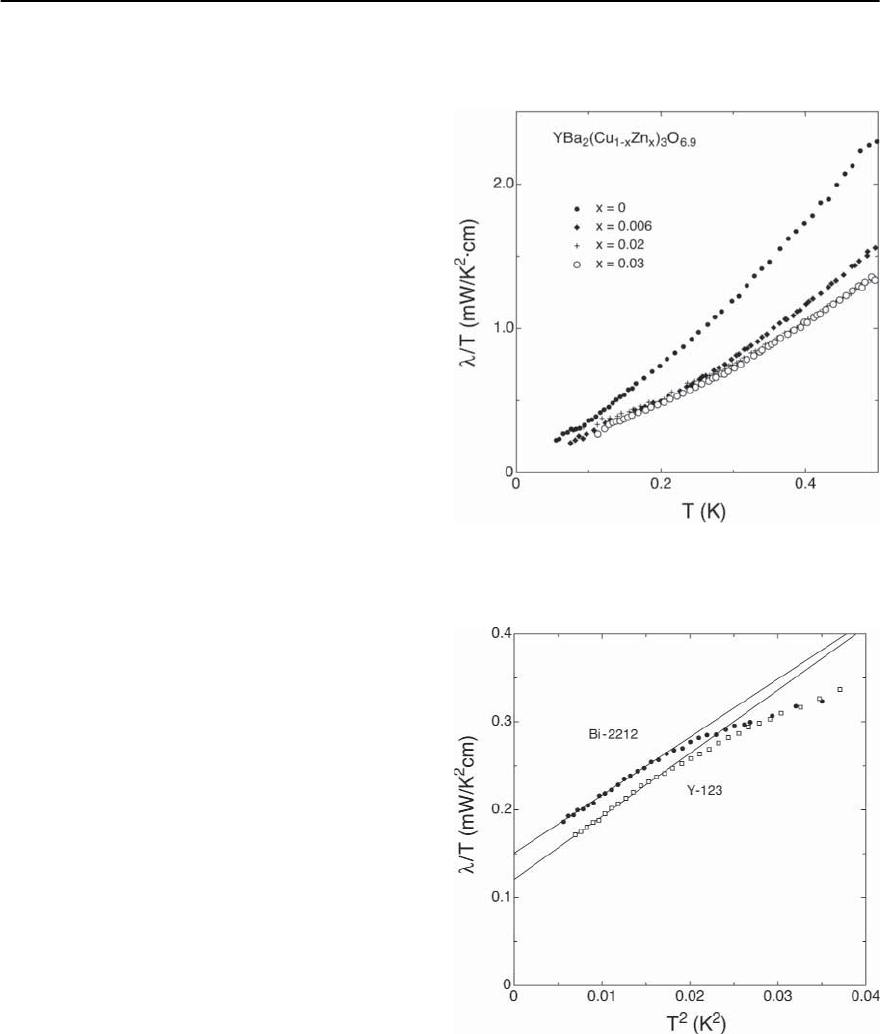
14 High-T

Superconductivity 805

Fig. 14.57.Another prediction [207,208] for the line

node configuration, the scaling of the anisotropic

component of the field induced specific heat, given

by C

(T, H||c)−C

(T, H⊥c) has also been inves-

tigated and confirmed experimentally [209]. Analo-

gous experiments with similar results and conclu-

sions, namely the presence of line nodes in the gap

function, have also been made on superconducting

1.85

0.15

CuO

[210].

As we have seen in one of the previous subsections,

the transport of energy or heat in the superconduct-

ing state of cuprate materials is mainly carried by

excited electronic quasiparticles. It may therefore be

expected that at very low temperatures, measure-

ments of the temperature dependence of the thermal

conductivity at temperatures much below T

again

provide results that are dictated by the gap config-

uration (k). In particular, again a rather general

theoretical prediction is available for the case of d-

wave typegapfunctionwithlinenodesintwodimen-

sions [211]. It addresses the quasiparticle transport

in such a system and states that this transport should

become independent of the scattering rate as T ap-

proaches 0 K. For a d-wave type gap configuration

it is known that impurities widen the zero gap re-

gions around the line nodes, thereby enhancing the

amount of remnant normal quasiparticles even at

T = 0 K. This enhancement is compensated by the

impurity imposed reduction of the mean free path,

thus resulting in a universal limit of the heat trans-

port. Relevant experimental data for testing this pre-

diction are available for heat transport parallel to the

Cu-O planes of YBCO-123 and Bi-2212 single crys-

tals [212, 213]. In Fig. 14.58 we show the measured

T dependence of the thermal conductivity along the

a axis of YBCO-123 single crystals, doped with dif-

ferent amounts of Zn impurities. It may be seen that

at the lowest temperatures, the ratio /T reaches a

value that is independent of the amount of impuri-

ties and hence the scattering rate. From these results

it is claimed that a universal value of /T does ex-

ist at very low concentrations of impurities [212].In

Fig. 14.59, a comparison of data obtained for the in

planethermalconductivity ofYBCO-123andBi-2212

single crystals confirms that a remnant normal com-

ponent 

, varying linearly with T,isobservedin

cuprate superconductors at T close to 0 K [213]. For

Fig. 14.58. Variation of the low temperature thermal con-

ductivity along the a-axis of single crystalline Y-123 upon

replacing Cu by Zn (see [212])

Fig. 14.59. Low temperature thermal conductivity of single

crystalline Y-123 and Bi-2212. The solid lines emphasize

the two contributions varying as T and T

, respectively

(see [213])

806 H.R.Ott

a d-wave gap configuration, the ratio 

/T may ap-

proximately be expressed as [214]





· n

3h · d





, (14.23)

where n/d is the stacking density of Cu-O planes,

and v

are the Fermi velocity, directed normal

to the constant-energy contour, and the quasiparti-

cle velocity tangential to the Fermi surface at each

node, respectively. It turns out that the ratio v

can be deduced from direct measurements of the

k-dependence of the gap function (see below) with

ARPES [215]. The values of v

,calculatedeither

from 

/T or from the ARPES data differ only in-

significantly, i.e., safely within experimental uncer-

tainties [213].

While these experimental findings strongly sup-

port that the pairing state of cuprate superconduc-

tors implies a gap functionwith linenodesin general

and a d-wave configuration in particular, the good

agreement of the values for v

from transport

and spectroscopic measurements tends to imply that

the quasiparticles act like those of a Fermi liquid, at

least at low energies. The pros and cons related with

the Fermi liquid description of the normal state have

been addressed in Sect. 14.4.1 above.

(d) Nuclear Magnetic Resonance

The first indications for unconventional supercon-

ductivity from NMR measurements probing the spin

lattice relaxation of Cu and O nuclear spins have

brieﬂy been mentioned in the introductory to sec-

tion of this subchapter. Here we first simply recall

that also the relaxation of nuclear spins via inter-

action with electronic quasiparticles is expected to

reveal the presence of a vanishing gap. This relax-

ation rate provided by this channel is expected to

vanish following a power law in T with decreasing

temperature and not exponentially as in the case of a

nodeless gap. That this is indeed observed is shown

in Fig. 14.55, where it may be seen that the reduction

of T

−1

below T

is definitely not exponential in 1/T.

Additional relevant information concerning the

gap and even the spin configuration of the pair state

can be obtained from the temperature dependence

of the Knight shift in the superconducting state. As

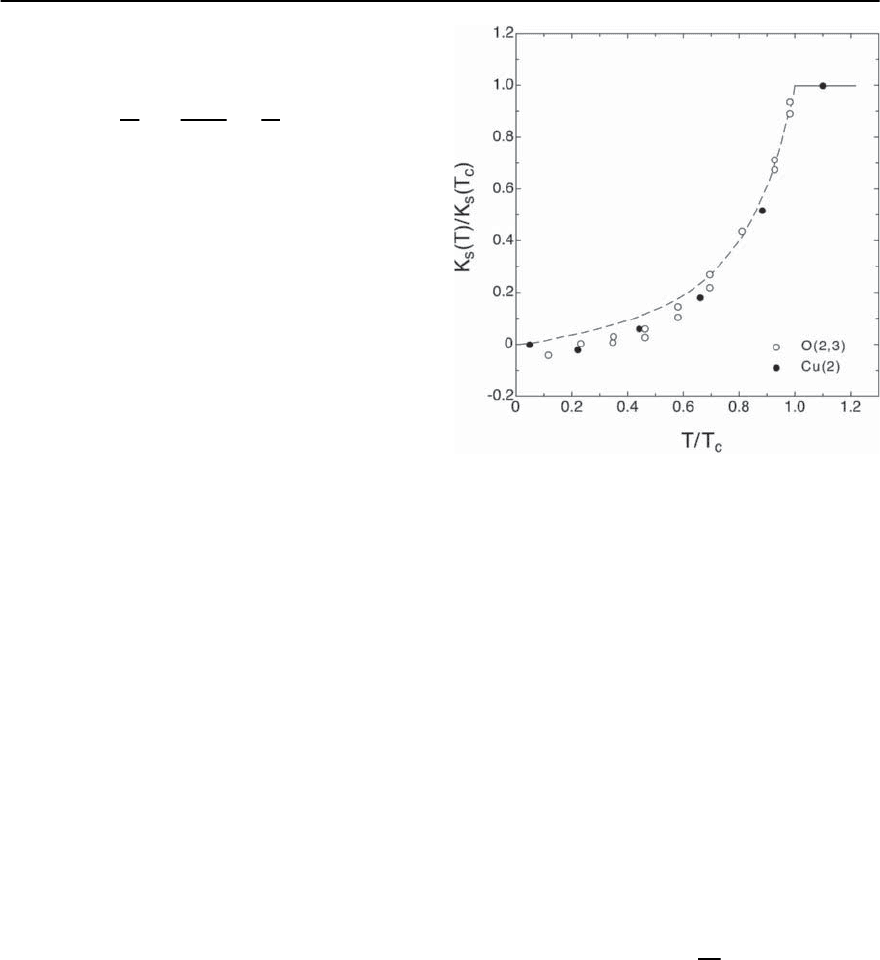
Fig. 14.60. Temperature dependence of the normalized

Knight shifts of Cu and O NMR signals in the supercon-

ducting state of Y-123. The broken line represents a cal-

culation based on gap function with d-wave symmetry

(see [191])

we have mentioned in Sect. 14.4.1 the Knight shift

K is, via its proportionality to the spin susceptibility



of the quasiparticles, proportional to the density

of quasiparticle states at the Fermi energy. For more

complex materials,such as the cuprate superconduc-

tors, other contributionsto the magnetic susceptibil-

ity have to be taken into account.

For conventional superconductors, where K may

simply be assumed to be proportional to the mag-

netic susceptibility and, below T

,thetemperature

dependence K(T) is given by the so called Yosida

function [216]. It results from the calculation of the

Pauli-type magnetic susceptibility in the supercon-

ducting state 

(T) which is given by



=−4



BCS

(E)



∂f

∂E



dE , (14.24)

whereD

BCS

= D(E

)·|E|/(E

−

),andf is theFermi–

Dirac distribution function. If the gap function  is

nodeless and the pairing is of spin singlet type, 

vanishes exponentially with decreasing temperature

for T →0 K.For spin triplet pairing the Knight shift

is unaffected by the superconducting transition, i.e.,