Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors
Подождите немного. Документ загружается.


22 A Spin Fluctuation Model for d-Wave Superconductivity 1361
propagators are then given by the Gor’kov expres-
sions, which for generality we present in the super-
conducting state,
G
k
(i!)=
i! + £
k
(i!)+"
k
(
(
i! + £
k
(i!)
)
2
− ¥
2
k
(i!)−"
2
k
, (22.9)
F
k
(i!)=−
¥
k
(i!)
(
i! + £
k
(i!)
)
2
− ¥
2
k
(i!)−"
2
k
, (22.10)
q
(
i!
)
=
˛
2
1+
2
(
q − Q
)
2
− ¢
Q
(
i!
)
. (22.11)
Here £
k
(i!)and¢
Q
(i!) are fermionic and bosonic
self-energies (k stands for the component along
the Fermi surface), and F
k
(i!)and¥
k
(i!)arethe
anomalous Green’s function and the anomalous self-
energy, respectively. In the next sections we compute
£
k
(i!), ¢
Q
(i!)and¥
k
(i!).
One can also motivate the spin fermion model by
following the approach developed by Landau in his
theory of Fermi liquids [9], i.e. by assuming that the
influence of the other fermionic quasiparticles on a
given quasiparticle can be described in terms of a set
of molecular fields [10, 36]. In the present case the
dominant molecular field is an exchange field pro-
duced by the Coulomb interaction U(q). However,
one has to consider this field as dynamic, not static.
The corresponding part of the action contains
S =−
dkG
−1
0
(
k
)
†
k,˛
k,˛
(22.12)
+
1
2
dq
dk
dk
†
k+q,˛
k,ˇ
†
k
+q,˛
×
k
,ˇ
0
˛ˇ,ı
(k, k
, q) ,
with bare four fermion interaction at low energies:
0
˛ˇ,ı
(k, k
, q)=−g
2
0
(q)
˛ˇ
ı
. (22.12a)
Formally, this can be obtained from (22.3) by inte-
grating out the collective degrees of freedom S.A
relation between this purely fermionic approach and
the bosonic spin susceptibility
(
q
)
of (22.11)can be
established by evaluating the four point vertex in the
spin channel within perturbation theory.We find
˛ˇ,ı
(k, k
, q)=−V
eff
(q)
˛ˇ
ı
, (22.13)
where the renormalized quasiparticle interaction is
proportional to the renormalized spin propagator
V
eff
(q)=g
2
(q) = (22.14)
×
g
2
˛
2
1+
2
(q − Q)
2
− ¢
Q
(i!)
.
22.2.2 Weak- Coupling Approach to the Pairing
Instability
One of the most appealing aspects of the spin-
fluctuation theory is that it inevitably yields an at-
traction in the d
x
2
−y
2
channel.As with any unconven-
tional pairing, this attraction is the result of a spe-
cific momentum dependence of the interaction, not
of itsoverallsign whichforspinfluctuationexchange
is positive, i.e. repulsive in the s-wave channel. This
differentiates spin induced pairing from the pairing
mediated by phonons. In the latter case, the effec-
tive interaction between fermions is negative up to
a Debye frequency. In configuration space the spin-
fluctuation interaction,(22.15),can easily seen to be
repulsive at the origin and alternate between attrac-
tion and repulsion as one goes to nearest neighbors.
It is always repulsive along the diagonals, and this
is why a d
x
2
−y
2
state, in which the nodes of the gap
are along the diagonals,is the energetically preferred
pairing state due to spin-fluctuation exchange [116].
Suppose first that the spin–fermion coupling is
small enough such that conventional perturbation
theory is valid. To second order in the spin–fermion
coupling,thespin mediated interactionhas the form
of (22.12a).
The total antisymmetry of the interaction implies
that the orbital part is symmetric when the spin part
is antisymmetric and vice versa. The orbital part of
the interaction at low frequencies has the same sign
as the propagator of optical phonons at ! < !
D
.
However, the spin part involves a convolution of
the Pauli matrices, and is different from phononic
ı
˛ˇ
ı
ı
− ı
˛ı
ı
ˇ
.Using
˛ˇ
ı
=2ı
˛ı
ı
ˇ
− ı
˛ˇ
ı
ı
we find
0
˛ ,ˇı
(q)=−g
2
0
(q)(T
˛ ,ˇı
−3S
˛ ,ˇı
) , (22.15)

1362 A.V. Chubukov, D. Pines, and J. Schmalian
where T
˛ ,ˇı
=(ı
˛ˇ
ı
ı
+ ı
˛ı
ı
ˇ
)/2andS
˛ ,ˇı
=
(ı
˛ˇ
ı
ı
− ı
˛ı
ı
ˇ
)/2 are triplet and singlet spin con-
figurations, respectively. We see that there is an ex-
tra minus sign in the singlet channel.This obviously
implies that in distinction to phonons, the isotropic
s-wave component of the interaction is repulsive, i.e.
isotropic s-wave pairing due to spin fluctuation ex-
change is impossible. There are two other possibili-
ties:unconventionalsingletpairing forwhich we will
need a partial component of
0
(q) to be negative, or
triplet pairing, for which the corresponding partial
component of
0
(q)shouldbepositive.
It turns out that for a spin susceptibility peaked
at or near the antiferromagnetic momentum Q,the
triplet components are all negative, and triplet pair-
ing is impossible. We therefore focus on singlet pair-
ing. The linearized equation for the pairing vertex
F
k
(i!
m
) in the singlet channel is
F(k)=−3g
k
F(k
)
0
(k − k
)G
0
(k
)G
0
(−k
) . (22.16)
If (k − k
) was independent of momentum, a so-
lution of this equation would not exist because of
the overall minus sign. In our situation, however, the
interaction predominantly occurs between fermions
that areseparated in momentum space by Q =(, )
(see Fig. 22.6). Since both k and k + Q should be
near theFermi surface,the pairing predominantly in-
volves fermions near hot spots k
hs
and k
hs
+Q.Asthe
hot spots are well separated in momentum space, we
can change the sign in the r.h.s. of (22.16) by requir-
ingthatthepairing gap changes sign betweenk
hs
and
k
hs
+ Q.Indeed,substitutingF
k+Q
(i!
m
)=−F
k
(i!
m
)
into (22.16), we find that both sides of this equation
havethesamesign.Thepairingproblemthenbe-
comes almost identical to that for phonons, and the
gap equation has a solution at some T
c
.
Altogether, there are N = 8 hot spots in the Bril-
louin zone; these form four pairs separated by Q,
between which the gap should change sign.This still
does not specify the relative sign of the gap between
adjacent hot spots.However,if the hot spots are close
to (0, ) and symmetry relatedpoints,as in optimally
doped cuprates,the gap is unlikelyto change sign be-
Fig. 22.6. A representative Brillouin zone and Fermi sur-
face for a near-optimally doped cuprate superconductor.
The hot spots are connected by the antiferromagnetic wave
vector Q =( , ).For a weakly incommensurate magnetic
response, the number of hot spots doubles but simultane-
ously the intensity of the magnetic response at momenta
connecting pairs of hot spots drops by a factor of two. The
net effect then remains the same as for the commensurate
response. The figure is taken from [49]
tween them. This leaves as the only possibility a gap
that vanishes along diagonal directions k
x
= ±k
y
,i.e.
it obeys d
x
2
−y
2
symmetry.
We emphasize that although we found that the
pairing gap necessarily should have d
x
2
−y
2
symme-
try, its momentum dependence is generally more
complex than simply cos k
x
−cosk
y
.Tounderstand
this, we consider how one can generally analyze
(22.16) [87]. A standard strategy is to expand both
the pairing vertex and the interaction in the eigen-
functions of the representations of the D
4h
symme-
try group of the square lattice. There are four singlet
representations of D
4h
labeled A
1g
, B
1g
, B
2g
and A
2g
.
The basic eigenfunctions in each representation are
1inA
1g
,cosk
x
−cosk
y
in B
1g
,sink
x
sin k
y
in B
2g
and
(cos k
x
−cosk
y
)sink
x
sin k
y
in A
2g
. Other eigenfunc-
tions in each representation are obtained by com-
bining the basic eigenfunction with the full set of
eigenfunctions with full D
4h
symmetry. Obviously,
the eigenfunctions with d
x
2
−y
2
symmetry belong to
B
1g
channel. The orthogonal functions in the set can
be chosen as d
n
(k)=cosnk
x
−cosnk
y
.
One can easily make sure that the pairing problem
close to T
c
decouples between different representa-
tions. Numerical calculations show that B
1g
compo-
nents are thelargest.We therefore neglectotherchan-

22 A Spin Fluctuation Model for d-Wave Superconductivity 1363
nels and focus only on B
1g
pairing. Still, there are
an infinite number of B
1g
eigenfunctions, and the
pairing problem does not decouple between them.
Indeed, expanding F
k
(!
m
)and
0
(k)ind
n
(k)as
F
k
=
p
F
p
d
p
(k),
0
(k − k
)=
p
p
d
p
(k)d
p
(k
)
andsubstituting theresult into(22.16) we obtain [87]
F
n
(i!
m
)=−3g
2
T
p,m
F
p
n
n,p
, (22.17)
where
n,p
=
d
2
k
4
2
d
n
(k
)d
p
(k
)
(!
m
)
2
+(
k
)
2
. (22.18)
We s ee that a ll
n,p
are nonzero for arbitrary n and
p as the products d
n
(k)d
p
(k)andG
0
(k)G
0
(−k)=
1/((!
m
)
2
+(
k
)
2
) are symmetric under D
4h
.Asare-
sult, (22.17) couples together an infinite number of
partial components F
n
. As long as the partial com-
ponents of the susceptibility are dominated by mo-
menta relatively far from Q,all
n
and hence F
n
are
ofthesameorder.Insomeparticularlatticemod-
els an RPA analysis shows that at ∼ 1,
1
is nu-
merically significantly larger than all other
n
[36].
In this situation, F
k
≈ F
1
d
1
(k), i.e. the momentum
dependence of the gap should closely resemble the
cos k
x
−cosk
y
form.In real space,this implies that the
pairing is local and involves fermions from the near-
est neighbor sites on the lattice. In models with dif-
ferent high-energy physics, other
n
may dominate.
Clearly, the momentum dependence of the gap is not
universal as long as the pairing is local in real space.
Universality is recovered when the susceptibility be-
comes strongly peaked at Q. In this limit (in which
we can also rigorously justify restricting our atten-
tion to the B
1g
channel [87]), all partial components
n
scale as log and differ only in sub-leading non-
logarithmic terms. A straightforward trigonometric
exercise shows that fornear-equal
n
,the pairing gap
is very different from cos k
x
−cosk
y
: it is reduced
near the nodes and enhanced near the maxima at
hot spots with the ratio of the gap maximum and the
slope near thenodesincreasing as
2
.Inthissituation
the pairing problem is confined to hot spots.
22.3 Summary of Strong-Coupling Theory
for Electron–Phonon Pairing
For phonon-mediated superconductivity, Eliashberg
theory offers a successful approach to study the sys-
tem behavior at strong coupling. It is justified by
Migdal’s theorem which states that the vertex correc-
tions, ıg/g and (1/v
F
)d£(k, i!)/dk,aresmalldue
to the smallness of the ratio of sound velocity and
Fermi velocity stemming from the smallness of the
ratio of the electronic and ionic masses. Eliashberg
has demonstrated that for £(k, i!) ≈ £(i!)and
g
tot
= g + ıg g, the phonon-mediated pairing
problem can be solved exactly.A review of Eliashberg
theory for the electron–phonon problem is given
in [117]. As we already pointed out, for spin fluc-
tuation induced pairing there is no Migdal theorem
simply because the spin propagator is made out of
electrons and hence a typical spin velocity is of the
same order as the Fermi velocity. It is therefore natu-
raltoinquirewhetherthis impliesthat anEliashberg-
type treatment is inapplicable to the spin problem.
To properly address this issue, we review the case of
electron–phonon interactions and examine why the
smallness of the mass ratio affects d£(k, i !)/dk but
not d£(k, i!)/d!.
The electron–phonon interaction is generally
rather involved and has been discussed in de-
tail in the literature [5]. For our purposes, it is
sufficient to consider the simplest Fr¨ohlich-type
model of the electron–phonon interaction in which
low-energy electrons are coupled to optical phonons
by a momentum, frequency and polarization inde-
pendent interaction g
ep
. Despite its simplicity, this
model captures the key physics of phonon-mediated
pairing.
The propagator of an optical phonon has the form
D(q, i !
m
)=
!
0
!
2
0
+ !
2
m
+(v
s
q)
2
. (22.19)
Here !
0
is a typical phonon frequency, which is of
the order of the Debye frequency, and v
s
is the sound
velocity. Both !
0
and v
s
are input parameters, unre-
lated to fermions. The ratio v
s
/v
F
scales as (m/M)
1/2
whereM is the ionicmass,and m is the electron mass.
In practice, v
s
/v
F
∼ 10
−2
[5]. This is a real physically

1364 A.V. Chubukov, D. Pines, and J. Schmalian
motivated small parameter for the electron–phonon
problem.
To make the analogy with spin fluctuations more
transparent, we will consider below the case when
!
0
v
s
/a, i.e. the correlation length for optical
phonons is large. This last assumption allows us to
simplify the calculations but will not change their
conclusions.
In the presence of two different velocities, it is
not aprioriobvious what is the best choice of a di-
mensionless expansion parameter in the theory. Two
candidate dimensionless parameters are
ep
= g
2
ep
/(4(v
s
v
F
)) (22.20)
(thefactor 4 is chosen for further convenience),and
˜
ep
=
ep
v
s
/v
F
∼ (g
ep
/v
F
)
2
. (22.21)
For simplicity, we set the lattice constant a =1.Ob-
viously,
ep
˜
ep
.Inpractice,
˜
ep
1forallrea-
sonable g
ep
while
ep
can be either small or large.
Which of the two dimensionless couplings ap-
pears in perturbation theory? Consider first the
lowest-order diagram for the spin–fermion vertex at
zero external frequency and zero bosonic momen-
tum withall fermionic momentaatthe Fermi surface.
Choosing T =0andthex axis along the direction
of v
F
of an external fermion, we obtain the vertex
correction in the form:
ıg
ep
g
ep
=
g
2
ep
8
3
d!
m
d
2
q
(i!
m
− v
F
q
x
)
2
!
0
!
2
0
+ !
2
m
+(v
s
q)
2
.
(22.22)
The evaluation of the momentum and frequency in-
tegrals is straightforward. On performing the inte-
gration we obtain for !
0
v
s
,
ıg
ep
g
ep
=
˜
ep
=
ep
v
s
v
F
. (22.23)
We see that the vertex correction scales as
˜
ep
and
is small. For !
0
∼ v
s
, the expression is more com-
plex but still is of order
˜
. One can easily check
that higher-order diagrams yield higher powers of
˜
ep
, i.e. are also small. This result, first obtained by
Migdal [118], is Migdal’s theorem.
The physics behind this result is transparent and
can be directly deduced from an analysis of the inte-
grand in (22.22).We see that the product of the two
fermionic Green’s functions yields a double pole at
q
x
= i!
m
/v
F
∼ !
0
/v
F
.Theintegraloverq
x
is then
finite only due to the presence of the pole in the
bosonic propagator which is located at a much larger
momentum q
x
∼ i!
0
/v
s
. This implies that the elec-
trons that contribute to the vertex correction are
oscillating not at their own fast frequencies but
at much slower phonon frequencies. At vanishing
v
s
/v
F
, fermions can be considered as static objects
with a typical q
x
∼ q
y
∼ !
0
/v
s
.Thetwodimensional
momentum integration over the product of two
fermionic propagators then yields O(1/v
2
F
). Simul-
taneously, the frequency integral over the bosonic
propagator yields D(q ∼ !
0
/v
s
, 0) = O(1). Combin-
ing the two results, we obtain ıg
ep
/g
ep
= O(
˜
)asin
(22.23).
We next consider the fermionic self-energy, see
figure above. Evaluating the Feynman diagram and
subtracting the contribution at ! =0, k = k
F
,we
obtain
£(k, i!
m
)=(i!
m
−
k
)I(k, i!
m
) , (22.24)
where
I(k, i!
m
)=g
2
ep
d§
m
d
2
q
8
3
!
0
!
2
0
+ §
2
m
+(v
s
q)
2
×
1
i§
m
− v
F
q
x
1
i(!
m
+ §
m
)−
k
− v
F
q
x
. (22.25)
We again have chosen the q
x
axis along the Fermi
velocity v
F
.
Suppose for a moment that I(k, i!
m
)isnon-
singular in the limit k → 0and!
m
→ 0. Then
thewavefunctionrenormalizationandthevelocity
renormalization are both expressed via I(0, 0). This
quantity can be evaluated in exactly the same way as

22 A Spin Fluctuation Model for d-Wave Superconductivity 1365
the vertex correction.Performingthe integration,we
find
I(0, 0) = −
˜
ep
. (22.26)
Substituting this into (22.24) we find v
−1
F
d£/dk =
−d£/d(i!)=
˜
ep
.As
˜
ep
1, this result, if true,
would imply that both derivatives of the self-energy
are small, i.e. the system is fully in the weak cou-
pling regime. The physical interpretation of this re-
sult would parallel that for the vertex correction:fast
electrons vibrate at slow phonon velocities, and this
well-out-of-resonance vibrationcannotsubstantially
affect electronic properties.
However,this result is incorrect; d£/d! is of order
ep
,not
˜
ep
.The origin ofthis apparent contradiction
lies in the singular behavior of I(k, i!
m
)inthelimit
of vanishing k and !
m
. To see this, we need to com-
pute I(k, i!) in (22.25) at small but finite ! and
k
.
An explicit computation yields
I(k, i!
m
)=−
˜
ep
+
ep
i!
m
i!
m
−
k
, (22.27)
demonstrating that I(0, 0) and the limit of I(k, i!)at
!,
k
→ 0 do not coincide. The additional contribu-
tion in (22.27) comes from the regularization of the
double pole in the integrand in (22.25) (mathemati-
cally this is similar to the chiral anomaly in quantum
chromodynamics [119]).
It is clear from (22.27) that I(k, i!
m
) has singular
low frequency and small momentum limits. Substi-
tuting (22.27) into (22.24), we find that the actual
self-energy is
£(k, i!
m
)=i
ep
!
m
−
˜
ep
(i!
m
−
k
) . (22.28)
We see t hat d£/d! scales with
ep
whereas v
−1
F
d£/dk
is proportional to
˜
ep
. At strong coupling,
ep
≥ 1,
this self-energy gives rise to a strong renormaliza-
tion of both the quasiparticle mass and the quasi-
particle wave function. Still, vertex corrections and
the renormalization of the Fermi velocity scale with
˜
ep
and are small.
To understand the physical origin of the distinc-
tion between the frequency and momentum depen-
dence of the fermionic self-energy, it is essential to
realize that the second, O(
ep
), term in (22.27) is not
caused by real electron–phonon scattering. Rather, a
careful examination of the structure of the expres-
sion for I(k, !
m
) shows that this term accounts for
the pole in the fermionic particle hole polarization
bubbleat small momentum and frequency [120,121].
This implies thatthefermionic self-energy is actually
caused by coupling of fermions to their own bosonic
collective modes, while phonons just mediate this
coupling.
The neglect of vertex corrections and v
−1
F
d£/dk
leads to the well known Eliashberg equations for
£
m
= £(i!
m
) and (in the superconducting state) the
pairing self-energy ¥
m
= ¥
(
i!
m
)
that also depends
only on frequency. For phonon-mediated supercon-
ductors, these equations have the form
£
m
= i
ep
T
2
n
(
!
n
− i£
n
)
D
(
i!
m−n
)
¥
2
n
+
(
!
n
− i£
n
)
2
, (22.29)
¥
m
=
ep
T
2
n
¥
n
D
(
i!
m−n
)
¥
2
n
+
(
!
n
− i£
n
)
2
. (22.30)
This set of equations is solved for a given D
(
i!
m
)
which by itself is only very weakly affected by
fermions. In the normal state and at ! !
0
,the
self-energy equation (22.29) reduces to the first term
in (22.28).
We have reviewed the derivation of these well
known equations to underline the physical ori-
gin of the applicability of the Eliashberg approach.
We see that the electron–phonon interaction gives
rise to two physically distinct classes of interac-
tion processes that contribute very differently to the
fermionic self-energy and vertex corrections. In the
first class, fast electrons are forced to vibrate at slow
phonon frequencies (i.e. phonons are in resonance,
but electrons are far from resonance). This gives
rise to both vertex and self-energy corrections, but
these are small (∝ v
s
/v
F
) and are neglected in the
Eliashberg theory. In the second class, phonons me-
diate an effective coupling between fermions and
their bosonic collective modes.This process involves
fermions with energies near resonance and phonons
far away from resonance, and yields a strong renor-
malization of the fermionic propagator. The appli-
cability of the Eliashberg approach is then based on

1366 A.V. Chubukov, D. Pines, and J. Schmalian
the fact that one has to include the phonon-mediated
scattering on collective modes, but can neglect the
direct scattering of electrons by phonons.
These insights into the origin of the applicability
of the Eliashberg theory will now be used to justify
a generalized Eliashberg approach for spin mediated
pairing.
22.4 Strong-Coupling Approach
to Spin–Fermion Interaction
As shown in the previous section, for electron
phonon interactions the smallness of vertex and ve-
locity renormalizations is caused by the small ra-
tio of the Bose velocity and the Fermi velocity. The
spin problemis qualitatively different.The bare spin-
fluctuation propagator,(22.6),describes propagating
magnons whose velocity c is expected to be of the
same order as the Fermi velocity, i.e. c ∼ v
F
.There
is then no a priori reason to neglect vertex and ve-
locity renormalizations. Fortunately, this argument
is not correct for the following reasons: First, as we
just found in case of electron–phonon interaction,
the fermionic self-energy in the Eliashberg theory is
insensitive to the ratio of sound and Fermi velocities.
The small ratio of v
s
/v
F
is only necessary to eliminate
regular terms in the self-energy,which are due to real
scattering by phonons. For these terms to be small,
bosons must be slow modes compared to fermions.
Second, phonons are propagating modes,i.e.they are
weakly damped. Spin fluctuations are not propagat-
ing modes, as a strong spin–fermion interaction at
low-energies changes the spin dynamics from prop-
agating to diffusive. Diffusive modes have a differ-
ent relationship between typical momenta and en-
ergies compared to ballistic ones, making them slow
modes compared to electrons simply because typical
spin fluctuation energies ! scale as q
2
rather than
q. Consequently spin fluctuationsare slow compared
to fermions for small q despite c ∼ V
F
,andtheregu-
lar terms in the fermionic self-energy again become
smaller than singular ones.
We will show that in dimensions between d =2
and d =3,d£
(
!
)
/d! scales as
3−d
where,we recall,
∝ is the dimensionless spin–fermion coupling,
while v
−1
F
d£/dk remains non-singular at = ∞ in
d > 2 and only logarithmically increases for d =2.
This implies that an Eliashberg-type approach near a
magnetic instability is fully justified for d > 2andis
“almost” justified for d = 2. In the latter case (which
is the most interesting because of the cuprates), we
will have to invoke an extra approximation (an ex-
tension to large N)tobeabletoperformcalculations
in a controllable way.
Our strategy is the following. We first establish
that one can indeed develop a controlled approach
to the spin fluctuation problem in the normal state,
see also[106].Nextweapply thistheory tothepairing
problem and show that there is indeed d-wave super-
conductivity caused by antiferromagnetic spin fluc-
tuations.Wediscussthe valueof T
c
near optimal dop-
ing and the properties of the superconducting state,
particularly the new effects associated with the feed-
back from superconductivity on the bosonic propa-
gator, since these distinguish between spin-mediated
and phonon-mediated pairings.
22.4.1 Normal State Behavior
For our normal state analysis we follow [49] and
perform computations assuming that the Eliash-
berg theory is valid, analyze the strong coupling
results, and then show that vertex corrections and
v
−1
F
d£
k
(
! =0
)
/dk are relatively small at strong cou-
pling.
We begin by obtainingthe full form of the dynam-
ical spin susceptibility as it should undergo qualita-
tive changes due to interactions with fermions. The
self-energy forthe spin susceptibility(that is the spin
polarization operator) is given by the convolution of
the two fermionic propagators with the momentum
difference near Q and the Pauli matrices in the ver-
tices. Collecting all combinatorialfactors, we obtain:
¢
q
(
i!
m
)
=−16¯g
2
d
2
kd§
m
(2)
3
G
k
(
i§
m
)
×G
k+q
(
i!
m
+ i§
m
)
. (22.31)
Here G
k
(
i!
m
)
is a full fermionic propagator
G
k
(
i!
m
)
=
1
i!
m
+ £
(
i!
m
)
− "
k
(22.32)

22 A Spin Fluctuation Model for d-Wave Superconductivity 1367
and £
(
i!
m
)
is the self-energy which remains to be
determined. In principle, even in Eliashberg theory,
this self-energy depends on the momentum compo-
nent along the Fermi surface. However, for compu-
tations of ¢
Q
(
i!
m
)
this dependence can be safely
neglected; both fermions in the fermion polariza-
tion bubbleshould be close to the Fermi surface, and
hence the momentum integration is necessarily con-
fined to a narrow region around hot spots.
The 2 + 1-dimensional integral over momentum
and frequency in (22.31) is ultraviolet divergent; this
implies that its dominant piece comes from high-
est energies which we have chosen to be O(). This
contribution,however, should not be counted as it is
already incorporated into the bare susceptibility. In
addition, ¢
Q
(
i!
m
)
contains a universal piece which
remains finite even if we extend the momentum and
frequency integration to infinity. The most straight-
forward way to obtain this contribution is to first
integrate over momentum and then over frequency.
One can easily make sure that for this order of limits,
the high-energy contribution is absent, and the full
¢
q
(
i!
m
)
coincides with the universal part. The in-
tegration is straightforward and on performing it we
obtain
¢
Q
(
i!
m
)
=−
|!
m
|
!
sf
, (22.33)
where the characteristic energy scale is the spin fluc-
tuation frequency,
!
sf
=
4
(v
F
−1
)
2
¯g sin
0
. (22.34)
We recall that
0
is the angle between the Fermi ve-
locities at the two hot spots separated by q ∼ Q.
In optimally doped cuprates,
0
≈ /2 and weakly
depends on q as long as one is far from momenta
connecting Fermi points along the zone diagonal.
Setting
0
= /2 and making use of (22.8), we ob-
tain
!
sf
=
4
v
2
F
−2
¯g
=
3
16
v
F
−1
. (22.35)
An analytical continuation of (22.33) to the real
frequency axis yields ¢
Q
(
!
)
= i|!|/!
sf
.Aswean-
ticipated, the coupling to low-energy fermions gives
rise to a finite decay rate for a spin fluctuation. As
typical spin frequencies are of order c
−1
∼ v
F
−1
,
at strong coupling, ≥ 1, the induced damping
term !/!
sf
∼ !/(v
F
−1
) is large compared to the
frequency dependent !
2
/(c
−1
)
2
term in the bare
susceptibility, i.e. the interaction with low energy
fermions changes the form of the spin dynamics
from a propagating one to a relaxational one. Neg-
lecting the bare frequency term, we obtain
q
! + i0
+
=
˛
2
1+
2
(
q − Q
)
2
− i!/!
sf
, (22.36)
The same purely relaxational dynamic spin suscepti-
bility was introduced phenomenologically by Millis,
Monien and Pines [33] to describe the spin dynamics
observed in NMR experiments on the cuprates.
We emphasize that the polarization operator,
(22.33), is independent of the actual form of the
fermionic self-energy £
k
hs
(
!
)
. The explanation of
why a k−independent fermionic self-energy does not
affect the polarization bubble at a finite momen-
tum transfer was given by Kadanoff [122] who an-
alyzed a similar problem for phonons. He pointed
out that the linearization of the fermionic energy
around k
F
is equivalent to imposing an approximate
Migdal sum rule on the spectral function A(k, !)=
−(1/)ImG
R
(k, !)
d
k
A(k, !)=1, (22.37)
where
k
= v
k
·
(
k − k
F
)
in our case. Expressing
G(k, !
m
)intermsofA(k, !) via the Kramers–
Kronig relation and making use of (22.37), one finds
¢(q, !)=−
i!
!
sf
∞
−∞
d!
df (!
)
d!
+ O(!
2
) , (22.38)
where f (!
) is the Fermi function. Equation (22.33)
then followsfrom the fact that f (!
)is1at!
=−∞
and 0 at !
=+∞.
We next determine the fermionic self-energy
£
k
(
i!
)
. In Eliashberg theory it is given by
1368 A.V. Chubukov, D. Pines, and J. Schmalian
£
k
(
i!
m
)
=−3g
2
d
2
qd!
m
(2)
3
q
(
i!
m
)
× G
k+q
(
i!
m
+ i!
m
)
. (22.39)
Consider first the self-energy at a hot spot. Introduc-
ing i
£
n
= i!
n
+ £
k
hs
(
i!
n
)
and q − Q = ˜q,weobtain
from (22.39)
£
k
hs
(
i!
m
)
=
−3¯g
(
2
)
3
d!
m
d
2
˜q
˜q
2
+
−2
1+
|!
m
|
!
sf
×
1
i
£
m+m
− v
F
˜q
⊥
, (22.40)
with ˜q
2
= ˜q
2
+ ˜q
2
⊥
. The integration over the compo-
nent ˜q
, parallel to the velocity v
k
hs
at k
hs
,iselemen-
tary and yields
£
k
hs
(
i!
m
)
=
3
g
8
2
v
2
F
d!
m
d˜q
⊥
(22.41)
×
1
˜q
2
⊥
+ q
2
0
˜q
⊥
− iq
E
,
where q
0
=
−1
1+
|!
m
|
!
sf
1/2
and q
E
=
£
m+m
/v
F
.
We next assume, and then verify, that a typical
˜q
⊥
q
0
. q
2
⊥
in the first term can then be ignored,
and the momentum integration yields
d˜q
⊥
1
˜q
2
⊥
+ q
2
0
1
˜q
⊥
− iq
E
≈
1
q
0
∞
−∞
d˜q
⊥
1
˜q
⊥
− iq
E
= isignq
E
= isign(!
m
+ !
m
) . (22.42)
On substituting this result into (22.42) and splitting
the frequency integral into several pieces,depending
on the sign of !
m
+ !
m
,weobtain
£
k
hs
(
i!
m
)
= i
0
−!
m
d!
m
1
√
1+|!
m
|/!
sf
, (22.43)
where is given by (22.8).The remaining frequency
integration is elementary and yields (see Fig. 22.7)
£
k
(
i!
m
)
= i
2!
m
1+
1+
|!
m
|
!
sf
. (22.44)
Fig. 22.7. The frequency dependence of the normal state
electron self-energy due to spin-fluctuation–fermion in-
teraction for a quasi-particle at a hot spot (from [49])
We now return to the approximation we made
above, that a typical ˜q
⊥
q
0
. Since the typical val-
ues for ˜q
⊥
, i.e. those which dominate the integral in
(22.42),are of order q
E
, the approximation is valid if
q
0
q
E
. Further, a typical internal frequency !
m
is
of order !
m
, hence q
E
∼|!
m
+ £(!
m
)|/v
F
and q
0
∼
(!
sf
2
)
−1
(|!
m
| + !
sf
)
1/2
∼¯g
1/2
(|!
m
| + !
sf
)
1/2
/v
F
.
At weak coupling, 1, the condition q
0
q
E
implies that ! ¯g/, i.e. at energies smaller that
¯g, the approximation is well justified. At strong cou-
pling and ! !
sf
, q
E
≈ !/v
F
, q
0
∼ !
sf
/v
F
,and
the criterion q
0
q
E
is again satisfied. Finally, at
strong coupling and ! > !
sf
, q
E
∼ q
0
(and both ore
of order (¯g!
m
)
1/2
/v
F
. In this limit, the approxima-
tion we made is qualitatively, but not quantitatively
correct.In order to develop a well controlled theoret-
ical framework for this limit, Abanov et al. [87,123]
developed a controllable 1/N approach by extending
the model to a large number of hot spots, N,inthe
Brillouin zone (N = 8 in the physical case), or, equiv-
alently, to a large number of fermionic flavors. This
allows an expansion in terms of 1/N. For large N,
q
0
/q
E
∼ N
2
, i.e. the approximation q
0
q
E
is justi-
fied. Another appealing feature of this
1
N
expansion
is that within it, vertex corrections and the depen-
dence of the self-energy of the momentum compo-
nent transverse to the Fermi surface are also small in
1
N
and can be computed systematically together with
the corrections to the frequency dependent part of
the self-energy [49]. To keep our discussion focused
on the key results, we will not discuss further the
details of the 1/N approach. Rather, we just empha-
size that (i) (22.44) is quantitatively correct even if

22 A Spin Fluctuation Model for d-Wave Superconductivity 1369
q
0
∼ q
E
and (ii) numerically the difference between
approximate and more involved “exact” results for
the fermionic £
k
hs
(!) is only few percent already for
aphysicalN [49].
We next analyze the functional form of (22.44).
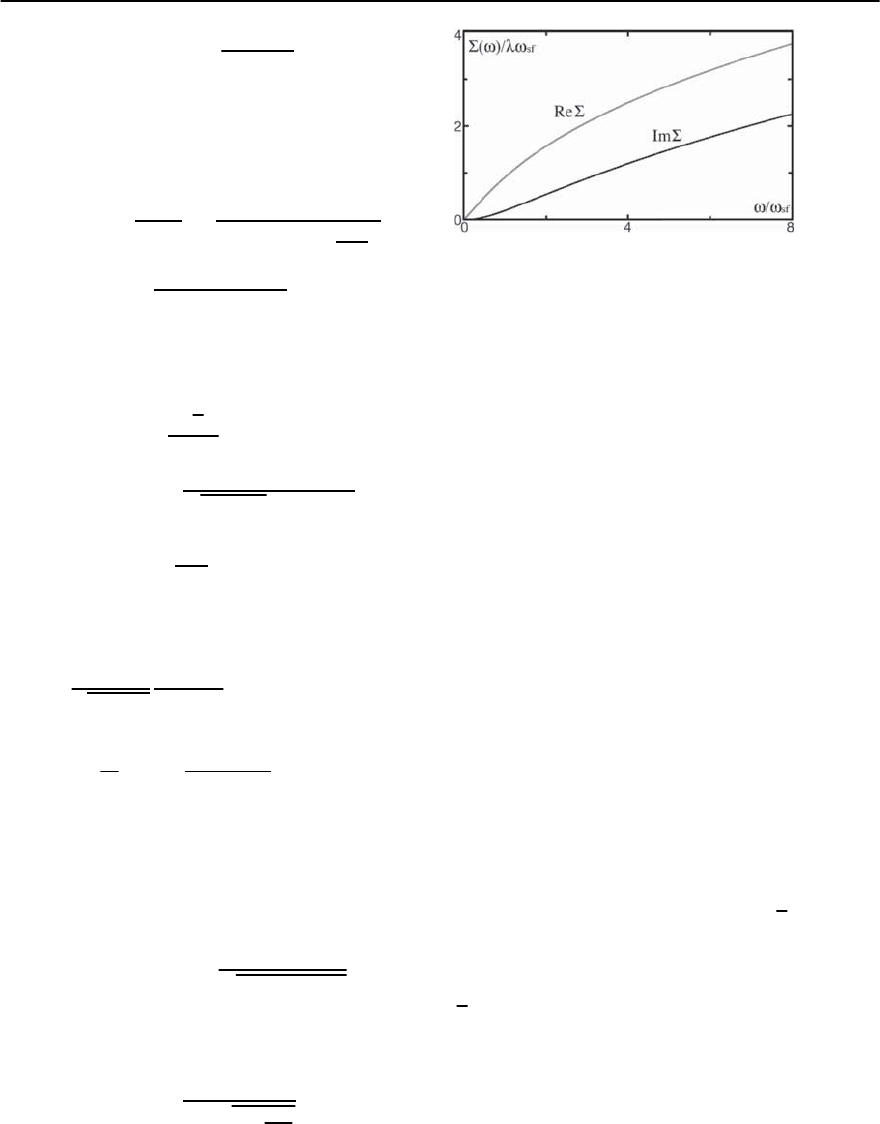
We se e t hat £
k
hs
(i!) scales with and at strong cou-
pling exceeds the bare i! term in the inverse fermion
propagator G
−1
k
hs
(i!)=i! − £
k
hs
(i!). As was the
case with phonons, it originates in the scattering on
zero-sound-like vibrations of the electronic subsys-
tem, while spin-fluctuations just mediate this inter-
action. Further, £
k
hs
(i!) (see Fig. 22.7) evolves at the
same typical energy !
sf
as the bosonic self-energy.
Thisinterconnectionbetweenbosonic and fermionic
propagators is one of the key “fingerprints” of the
spin–fermion model.
In Fig. 22.8 we show the behavior of the quasi-
particle spectral function A(
k
, !)atvarious
k
.We
see that the spectral weight of the quasiparticle peak
rapidly decreases as
k
becomes larger than !
sf
.
For small frequencies,! !
sf
,the spin suscepti-
bility can be approximated by its static form. For the
fermionic self-energy we find after analyticalcontin-
uation to real frequencies
£
k
hs
(
!
)
=
! +
i! |!|
4!
sf
;(! !
sf
) . (22.45)
We see that the quasiparticle damping term,although
quadratic in ! as it should be in a Fermi liquid,
scales inversely with !
sf
, not with the Fermi en-
ergy as in conventional metals. As !
sf
vanishes at
the critical point, the width of the Fermi liquid re-
gion, where damping is small compared to !,pro-
gressively shrinks as increases. The quasiparticle
renormalization factor d£
k
hs
(!)/d!|
!=0
= ∝
increases as the system approaches the magnetic
quantum critical point.The quasiparticle z-factorsi-
multaneously decreases as
z
k
hs
=
1
1+
∂£
k
hs
(
!
)
∂!
!=0
=
1
1+
(22.46)
and vanishes at criticality.
At frequencies above !
sf
, the imaginary part of
the fermionic self-energy resembles a linear func-
tion of ! over a substantial frequency range up to
Fig. 22.8. The normal state spectral function. Note the ab-
sence of a quasiparticle peak.This is the consequence of the
proximity to an antiferromagnetic quantum critical point.
The figure is taken from [49]
about 8!
sf
.Atlarger!, the self-energy eventually
crosses over to
£
k
hs
(
!
)
=sign!
(
i ¯!|!|
)
1/2
, (22.47)
where
¯! =4
2
!
sf
=
9
16
¯g . (22.48)
Observe that ¯! remains finite as →∞.Atthe
critical point !
sf
→ 0, the self-energy displays
the non-Fermi-liquid behavior of (22.47) down to
! = 0. A plot of the fermionic self-energy is pre-
sented in Fig. 22.7. The intermediate quasi-linear
regime is clearly visible.Notealso that the deviations
from Fermi liquid behavior starts already at small
! ∼ !
sf
/2.
We now consider how well the Eliashberg approx-
imation is satisfied, i.e. whether vertex corrections
and the momentum dependent piece in the fermionic
self-energy are relatively small. To do this one needs
to evaluate £
k
(! =0)atk = k
hs
and the vertex cor-
rection ıg/g. The details of the derivation can be
found in [49].We have
£
k
(
! =0
)
=
3
4
log
"
k+Q
(22.49)
and
ıg
g
=
Q(
0
)
8
log , (22.50)

1370 A.V. Chubukov, D. Pines, and J. Schmalian
where Q(
0
)=2
0
/.For
0
≈ /2, Q ≈ 1. We see
that these two corrections depend only logarithmi-
cally on the coupling and at large are parametri-
cally small compared to the frequency dependence of
the self-energy. Furthermore, at large N,bothıg/g
and £
k
contain an extra factor of 1/N, i.e., scale as
(1/N)log. We see therefore that (1/N)log is the
analog of the second coupling constant
˜
ep
for the
phonon case. Just as for phonons, the applicability
of the Eliashberg theory is related to the fact that
this second coupling constant is much smaller than
the primary coupling . In our case, this requires
that (log )/N. We however emphasize that
the smallness of the two “couplings”is not the result
of the smallness of the velocity ratio but the conse-
quence of the proximity to a critical point, when rel-
evant frequencies are small, and the O(!)damping
term in the spin propagator dominates over the !
2
term.Also,in distinctionto phonons,thesecondcou-
pling still diverges at the critical point and therefore
corrections to Eliashberg theory cannot be neglected
close to the antiferromagnetic transition.These cor-
rections have been analyzed within a renormaliza-
tion group approach in [49,124] and found to be of
minor relevance at intermediate coupling discussed
here.
It is also instructive to explicitly compute the
fermionic self-energy in the same way as we did in
Sect. 22.3 for systems with electron–phonon interac-
tion, and verify that the reason for the dominance
of the frequency dependence of the self energy is
common to that for the phonon case. To see this, we
introduce, by analogy with (22.24)
£(k, i!
m
)=(i!
m
−
k+Q
)I(k, i!
m
) . (22.51)
Evaluating I(k
hs
, i!
m
)inthesamewayasinthe
phononcase[49],wefindat! !
sf
I(k
hs
, i!
m
)=I
reg
+
i!
m
i!
m
−
k+Q
, (22.52)
where I
reg
= O(log ). This form is the same as that
found for phonons (see (22.27)). The analogy im-
plies that the dominant, O(), contribution to the
fermionic self-energy comes from magnetically me-
diated interactions between fermions and their col-
lective particle-hole excitations, whereas the actual
spin–fermion scattering process in which fermions
at forced to vibrate at typical spin frequencies yields
a smaller O(log ) contribution.
Finally, away from hot spots but still at the Fermi
surface, the fermionic self-energy is given by the
same expression, (22.44), as at a hot spot, but with
a momentum dependent coupling constant
k
and
energy scale !
sf
(k)whichobey
k
= /(1 + ık),
!
sf
(k)=!
sf
(1 + ık)
2
, (22.53)
where ık = |k
F
−k
hs
| is the momentum deviation
from a hot spot along the Fermi surface.We see that
the effectivecoupling decreases upon deviation from
a hot spot,while the upper energy scale for the Fermi
liquid behavior increases. The increase of !
sf
,how-
ever, is counterbalanced by the fact that !
sf
∝ sin
0
,
and
0
,which we had set to be ≈ /2,increases away
from a hot spot [125].
We see from (22.53) that the width of the re-
gion where £
k
(!) is independent of k (i.e. the “size”
of a hot spot) depends on frequency. At the low-
est frequencies, ! < !
sf
(k), £
k
(!)=i
k
!,and
the hot spot physics is confined to a region of
width
−1
which progressively shrinks as increases.
However, at frequencies above !
sf
(k), £
k
(!) ∼
k
(i!!
sf
(k))
1/2
= (i!!
sf
)
1/2
is independent of k.
Accordingly, physicalprocesses that happen on these
scales are isotropic (apart from the dependence on
0
). In this sense the whole Fermi surface acts as one
big “hot spot”.
One can easily perform the above analysis in di-
mensions larger than d = 2.One finds that the quasi-
particle spectral weight behaves for large and the
lowest energies ! < !
sf
as
z
k
hs
∝
d−3
(22.54)
for 2 < d < 3, and vanishes logarithmically for
d = 3. Correspondingly, in the quantum critical
regime we find for the self-energy along“hot lines”
£
k
hs
(
i!
)
∝ i! |!|
d−3
2
. (22.55)
This expression transforms into £
k
hs
(
i!
)
∝
i! log
(
|!|
)
for d =3.Aboved = 3 no non-Fermi
liquid effects result from the proximity to the quan-
tum critical point. This demonstrates that many of
