Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors

Подождите немного. Документ загружается.

18 Neutron Scattering and the Magnetic Response of Superconductors 1009

Table 18.1.Contributions to M

 in a ferromagnet and S =

2D antiferromagnet.

The table illustrates the total moment sum rule

M

(

)

Ferromagnet 2-D S =

antiferromagnet

Bragg peaks g

(0.061gS)

=0.37

Spin waves g

S 1.7

Multi-magnon 0 0.93

Total g

S(S +1) 3

(ii) one-magnon excitations and (iii) multimagnon

excitations. The sum of these contributions is gov-

erned by the moment sum rule (Eq.18.12).Table18.1

summarizes the spectral weights of the these contri-

butions as determined from a 1/S expansion the-

ory [88].

Linear Spin-Wave Theory for Nearest Neighbour

Interactions

The coupling between neighbouring spins in a

square-lattice antiferromagnet is described by the

Heisenberg Hamiltonian,

H =



J S

· S

. (18.16)

Conventional spin-wave theory of the Holstein–

Primakoff type, in the classical large-S limit, yields

the transverse dynamic susceptibility





⊥

(Q, !)=Z

(!)







1− (Q)

1+ (Q)



1/2

× ı

(

! ±!(Q)

)

, (18.17)

where,

!(Q)=2Z



1−

(Q)



1/2

, (18.18)

and  (Q)=

[

cos(2h) + cos(2k)

]

.Wehavein-

cluded a “quantum renormalisation” of the overall

spin-wave amplitude Z

(!)(ifZ

is constant then

= Z



). For the conventional linear spin-wave

model applicable for large S, Z

(!)=1.Inorder

to make comparisons with neutron scattering and

nuclear resonance experiments, it is useful to cal-

culate the“local” or“wavevector-integrated”energy-

dependent susceptibility 



(!) defined by Eq. 18.7.

In the low frequency limit Eq. 18.17 yields,





⊥

(!)=

(!)g



. (18.19)

Magn etic Excitations in La

CuO

Early measurements were performed on a conven-

tional reactor source using an “energy integrating”

technique [89,90] in which the two-dimensionality

of the magnetic interactions was exploited and the

magnetic response was integrated in energy up to

about 30 meV. This method allowed the weak signal

to be seen in relatively small single crystals. The spin

ﬂuctuations were shown to have a wide energy scale

(> 10 meV).

Subsequent experiments were performed using

epithermal neutrons produced by the “hot” source

at the Institute Laue–Langevin. The use of the

hot source allowed the spin-wave dispersion to be

followed up to 140 meV and the two counter-

propagating branches to be resolved [91, 92]. At

T=5 K, the spin-wave velocity was found to be

=0.85 ± 0.03 eV Å. Using the low-frequency

limit of Eq. 18.18, v

= Z

√

8SJa and assuming

=1.18 [88,93] yields a Heisenberg coupling con-

stant J = 136 ± 5 meV. In spite of the use of the

hot source and 0.1 kg of aligned single crystal, the

highest energy which could be achieved by reactor-

based three-axis methods was about 140 meV. Spal-

lation sources offer low background and high inci-

dent energies. The use of chopper spectrometers at

the ISIS spallation source allowed the zone bound-

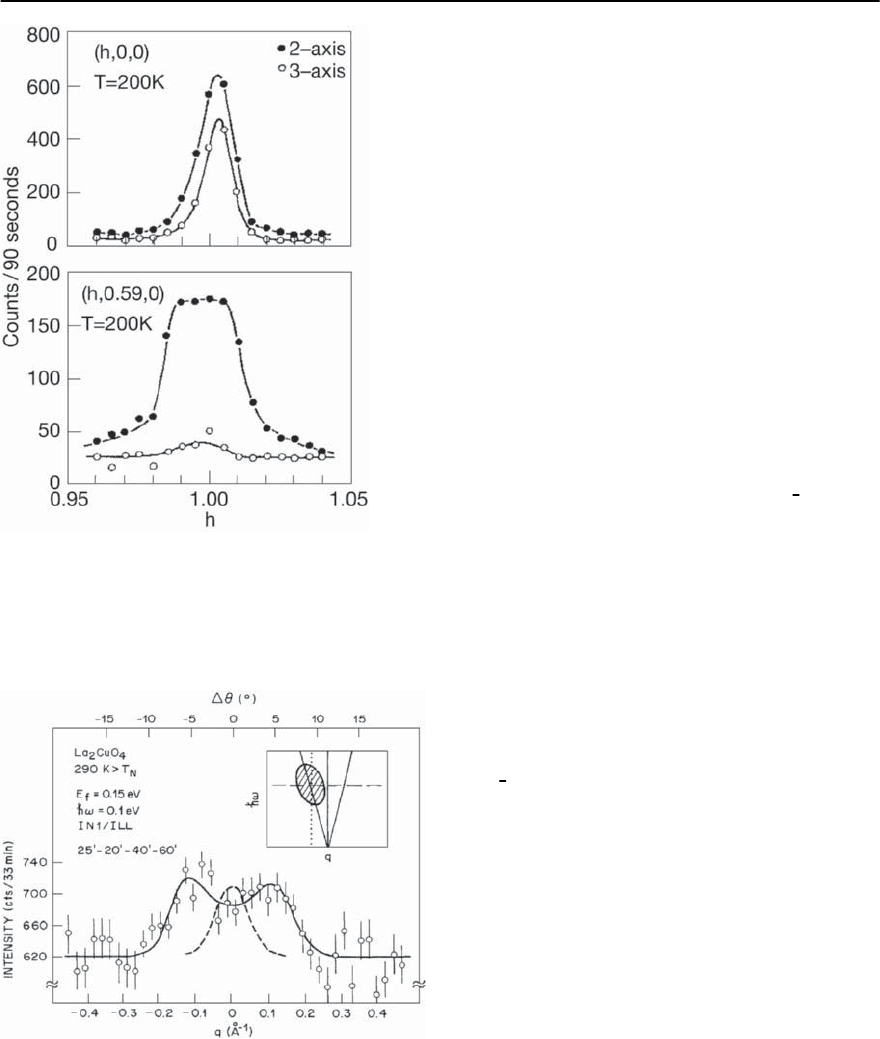
1010 S.M. Hayden

Fig. 18.19. Spin wave excitations in La

CuO

. Open circles

are scans with an energy window of about 1 meV around

zero. Closed circles correspond to an energy integration of

about 10 meV. The lower f igure demonstrates the existence

of magnetic excitations with an energy scale greater than

the integration window. After Shirane et al. [90]

Fig. 18.20. Hot source measurements of spin waves

in La

CuO

. The figure shows two resolved counter-

propagating spin waves. After Aeppli et al. [91]

ary single-magnon excitation to be measured [94].

The value of J determined from this early ISIS ex-

periment was J = 132 ± 4 meV. Improvements in

the ISIS instrumentation led to a considerable in-

crease in the wavevector resolution of which allowed

a subsequent measurement to resolve the detailed

dispersion throughout the Brillouin zone.

The linear spin-wave theory for a 2D square lattice

antiferromagnet (2DAF) with nearest neighbour in-

teractions described in the previous section predicts

that there is no dispersion in the magnon excita-

tions around the antiferromagnetic Brillouin zone

boundary, for example, along the line connecting

Q = (1/2,0) and (1/4,1/4) or (3/4,1/4). This lack of

dispersion is illustrated in Fig. 18.18. The measured

magnon dispersion in La

CuO

isshownin Fig.18.21.

In fact the magnon in La

CuO

shows a 7.5 % in-

crease in energy between (3/4,1/4) [or (1/4,1/4)] and

(1/2,0)[95].Adeviationof6%intheoppositesense

is observed in the another model S =

2D anti-

ferromagnet, Cu(DCOO)

· 4H

0 [96]. Two possible

explanations of the observed deviations have been

proposed. The first is that low-order spin wave the-

ory fails to account for the high energy dynamics

of the Heisenberg model because of the quantum

ﬂuctuations inherently present in the ground state

of the 2D Heisenberg model [97–100]. The second

is that a nearest-neighbour Heisenberg Hamiltonian

does not describe La

CuO

and higher order ex-

change terms such as cyclic exchange are required

to describe La

CuO

. Monte Carlo simulations of a

S =

2D Heisenberg model [98, 99] suggest a 10

% decrease in the magnon energy between (1/4,1/4)

and (1/2,0), the opposite to experiment.Thus the ob-

served magnon dispersion must be largely due to

longer range exchange interactions.

The exchange coupling constant J has been dis-

cussed widely in the literature (see, for example

[101]). Our understanding is based on Anderson’s

theory of superexchange [102] in which J ≈ 4t

/U.

Theoverlapofthecopperd orbitals and the oxygen

p orbitals is characterized by the hopping parame-

ter t and U represents the on-site interaction (in the

oxygen orbital). Fig. 18.13 illustrates the valence or-

bitals for a Cu

plaquette in La

CuO

. The large

orbital hybridizationin the CuO

planes provides an

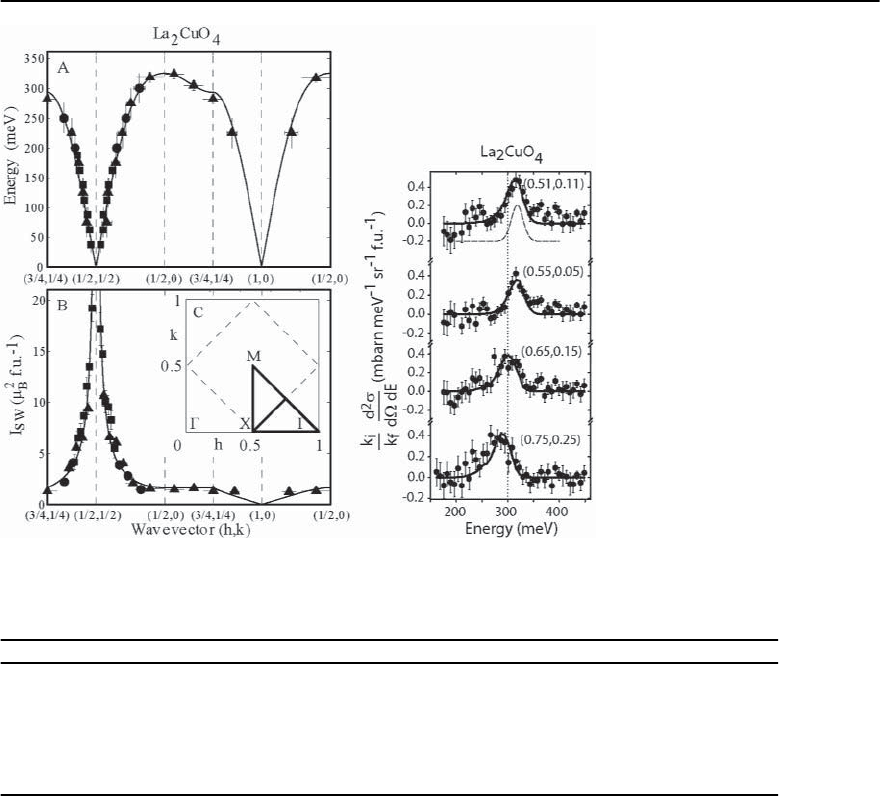
18 Neutron Scattering and the Magnetic Response of Superconductors 1011

Fig. 18.21. Left:Spinwavedis-

persion of La

CuO

. Right :Zone

boundary spin waves (after [95])

Table 18.2.Experimentally determined exchange constants for antiferromagnetic La

CuO

and related compounds. J has

been corrected for the effect of quantum ﬂuctuations which are expected to renormalise the bare exchange constants

∗

= Z

J,withZ

≈ 1.18 (see Sect. 18.6.2).

Composition Ref. T(K) J



(meV) J

(meV)

CuO

Aeppli et al. [91] 290 136 ± 5

CuO

Hayden et al. [94] 296 132 ± 4

CuO

Coldea et al.[95] 295 138 ± 438±8

CuO

Coldea et al.[95] 10 146 ± 461±8

CuO

Bourges et al. [103] 17 155 ± 3

CuO

Bourges et al. [103] 18 121 ± 3

exchange path to include all four spins at the cor-

ners of elementary Cu

plaquettes. Second near-

est neighbour Heisenberg exchange paths are also

possible. Measurements of the magnon dispersion

cannot distinguish between next-nearest neighbour

two-spin exchange and cyclic exchange terms of the

form [95]

H = J



i,j,k,l

·S

)(S

· S

)

+(S

·S

)(S

·S

)−(S

· S

)(S

· S

)

, (18.20)

where the spins are labelled clockwise around a

square plaquette.

A one-band Hubbard model provides a natural

understanding of the observed spin wave dispersion

for La

CuO

in terms of the Hubbard parameters t

and U. If hopping is included up to order t

(i.e.

four hops), a fit to the observed dispersion yields

the values t =0.33 eV and U =2.9 eV [95]. The fact

that higher order exchange terms are required to de-

scribe the dispersion relation in La

CuO

suggests

that longer range exchange interactions may also be

important in doped and superconducting composi-

tions.

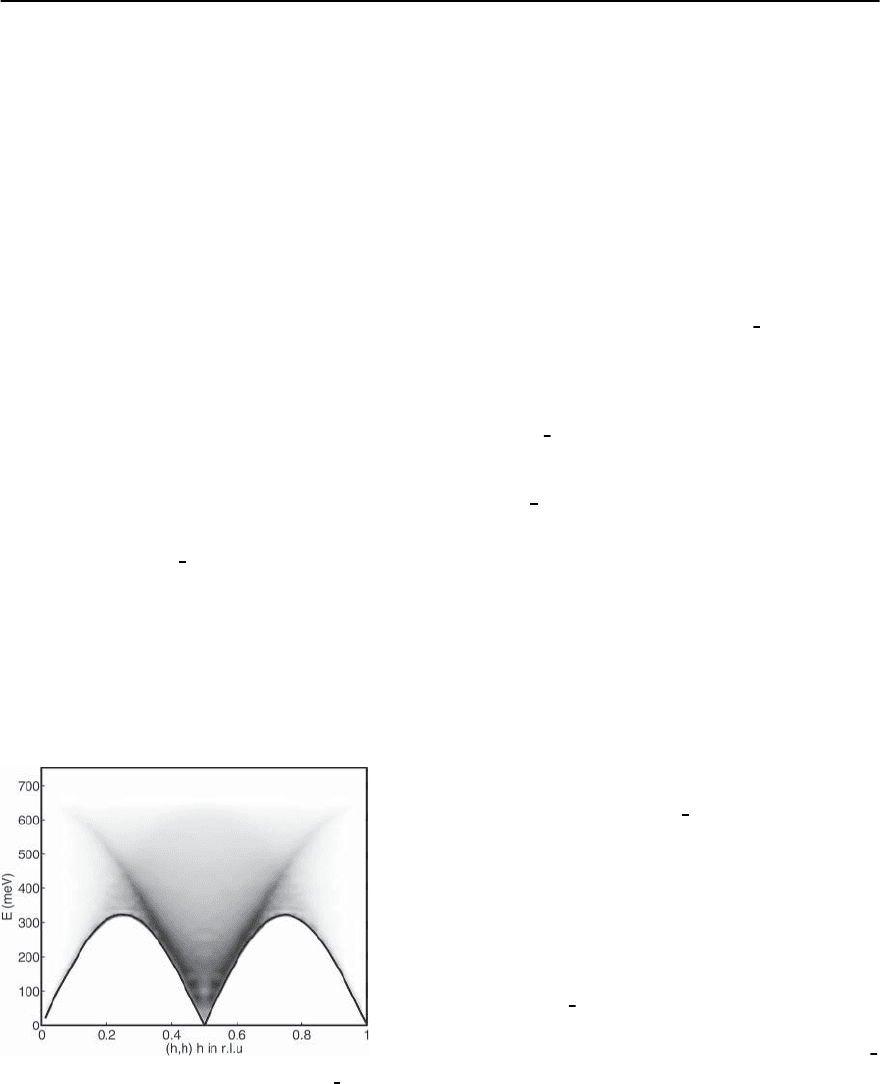
1012 S.M. Hayden

Multi-Magnon Excitations

A Heisenberg ferromagnet has two interesting prop-

erties not shared by the Heisenberg antiferromagnet.

The fully aligned ferromagnetic state is the ground

state (and an eigenstate) of the Hamiltonian. In ad-

dition, spin wave states are also eigenstates of the

Hamiltonian. In contrast,the Neel state (in which the

moments on each site do not ﬂuctuate with time) is

not the ground state an antiferromagnetic Heisen-

berg Hamiltonian. For small S, quantum ﬂuctua-

tions [88] become important. Quantum ﬂuctuations

lead to a number of effects: (i) a reduction of the

ordered moment; (ii) renormalisation of the spin-

wave energies and intensities; (iii) the existence of

multi-magnon excitations. Thus, in addition to the

single-magnon modes, two-magnon excitations give

rise to a continuum, as a function of energy, in the

longitudinal response 



(q, !), and three-magnon

excitations results in side bands (to the one-magnon

excitations) in the transverse response



⊥

(q, !).Fig-

ure 18.22 shows a calculation of the two-magnon re-

sponse for a 2D S =

square lattice antiferromag-

net [104,105].

Quantum effects lead to the renormalisation of

the (one-magnon) spin-wave dispersion, the perpen-

dicular susceptibility,the spin-stiffness constant,and

the sub-lattice magnetization with respect to clas-

sical (large-S) spin-wave theory. These renormalisa-

tion factors havebeen estimatedby a number of tech-

Fig. 18.22. Two-magnon excitations in a S =

square lat-

tice antiferromagnet. Calculation details are given in [104]

and [105]

niques. For the purpose of comparing theory and ex-

periment in the present review,we include the renor-

malisation of the overall energy scale in the exchange

constant, J

∗

= Z

J,whereJ is the “bare” exchange

constant occurring in Eq. 18.16. We have previously

defined the renormalisation of the amplitude of the

magnetic response in Eq.18.17.We note that,in prin-

ciple, these factors are energy dependent. The value

of Z

(!) can be obtained from neutron scattering,

if measurements are placed on an absolute intensity

scale. However, Z

cannot be measured directly from

inelastic neutron scattering and must be estimated

from theory. In the case of the S =

square-lattice

antiferromagnet, Singh [88] has estimated Z

=1.18

and Z

(! = 0)=0.61.

The 2D S =

Antiferromagnet at Finite Temperatures

Since the 1950s, it has been widely believed that the

2D S =

square-lattice antiferromagnet has long

range order only at T = 0.Anderson [85],argued that

eventhrough the staggered magnetization may be re-

duced, the N´eel state is still stable against quantum

ﬂuctuations at T = 0. Anderson’s assertion means

that this model system is an example of a “quantum

critical”phase transition i.e.one which occurs at zero

temperature and is therefore dominated by quantum,

ratherthan classical,ﬂuctuationsin theorder param-

eter. It was not surprising that the discovery of the

antiferromagnetism in La

CuO

and related com-

pounds rejuvenated theoretical [93,106–108] and ex-

perimental [89] interest in this problem. The liter-

ature devoted to the S =

square-lattice antifer-

romagnet is now vast, indeed there are several re-

views [107] on this subject.

One of the novel features of low dimensional an-

tiferromagnets,in particular 2D antiferromagnets,is

the strong build up of “critical” magnetic ﬂuctua-

tions at temperatures considerably above the order-

ing temperature. This behaviour is not at all con-

fined to S =

(see, for example, the review by De

Jongh and Miedema [109]). Figure 18.23 illustrates

the magnetic excitation spectrum for a 2D S =

antiferromagnet at finite temperature. For small fre-

quencies and wavevectors, propagating excitations

are believed not to exist, instead the response is

18 Neutron Scattering and the Magnetic Response of Superconductors 1013

Fig. 18.23. Schematic representation of the magnetic re-

sponse in a 2D antiferromagnet at finite temperature

dominated is a ‘quasielastic peak’ (i.e. 



(q, !)/!

is peaked at zero frequency). Since this peak domi-

nates the response for wavevectors near the ordering

wavevector, its width in wavevector is usually char-

acterized by the inverse correlation length 

−1

ob-

tained from the width of S(Q), the Fourier transform

of the equal-time correlation function.In the regime

!  v



−1

is the spin-wave velocity) spin-wave

interactions are the main mechanism for damping.

Grempel [110] estimated the order-parameter re-

laxation rate for q = 0 using a coupled-mode cal-

culation and found that 

 v



−1

(T/2

)

Chakravarty et al. [93, 106] have obtained defini-

tive results for the low-frequency response. They

showed that the long-wavelength, low-energy prop-

erties were well described by a mapping to a classical

two-dimensional Heisenberg magnet. The effects of

quantum ﬂuctuationsare absorbed intothe coupling

constants. Using this approach and Monte Carlo sim-

ulationstheyfoundthatthe temperaturedependence

of the correlation length  is,

 = C



a exp



2



. (18.21)

At energies larger than a few v



−1

,propagating

spin waves should exist and the response is believed

to be essentially as for T =0,exceptthatwemust

average the direction of the antiferromagnetic mo-

ment. The high frequency magnetic excitations see

the moment in the “quasielastic peak” as frozen do-

mains of size .

Magn etic Excitations in Antiferromagnetic YBa

YBa

is made up of pairs of CuO

planes, these

‘bilayers’ are then stacked together. Band structure

calculations [111, 112] suggest that there is a mod-

est electronic coupling between neighbouring Cu

atoms in different planes of the bilayer. This leads

to a inter-planar hopping parameter t

⊥

≈ 0.3 eV .

The resulting bilayer splitting in the band struc-

ture has been observed by angle-resolved photoe-

mission spectroscopy (ARPES) [74] in the related bi-

layer high-T

system Bi

CaCu

8+ı

. The electron

coupling between the two planes which make up the

bilayer also results in an inter planar exchange cou-

pling J

⊥

. The structure of the tetragonal insulating

phase of YBa

and the largest exchange cou-

plings are illustrated in Fig.18.14.Inorder toaccount

for the exchange coupling between Cu spins in dif-

ferent layers we add a second term to Eq. 18.16,

H =





·S





⊥

· S



. (18.22)

The presence of the second term (i.e. J

⊥

=0)in

Eq.18.16leads to the existence of two branches in the

spin-wave dispersion which can be labelled accord-

ingto whether neighbouring spinsin different planes

precess out-of-phase (“acoustic” or “odd” mode) or

in-phase (“optical”or“even”mode) abouttheir time-

averaged (ordered) directions. In the conventional

linear spin-wave approximation,the acoustic and op-

tic modes have the response functions per formula

unit [6]





odd

(Q, !) = (18.23)

 g





1− (Q)+J

⊥

/2J



1+ (Q)



1/2

× sin



zl



(

! ±!

odd

(Q)

)

and





even

(Q, !) = (18.24)

 g





1− (Q)

1+ (Q)+J

⊥

/2J





1/2

×cos



zl



(

! ± !

even

(Q)

)

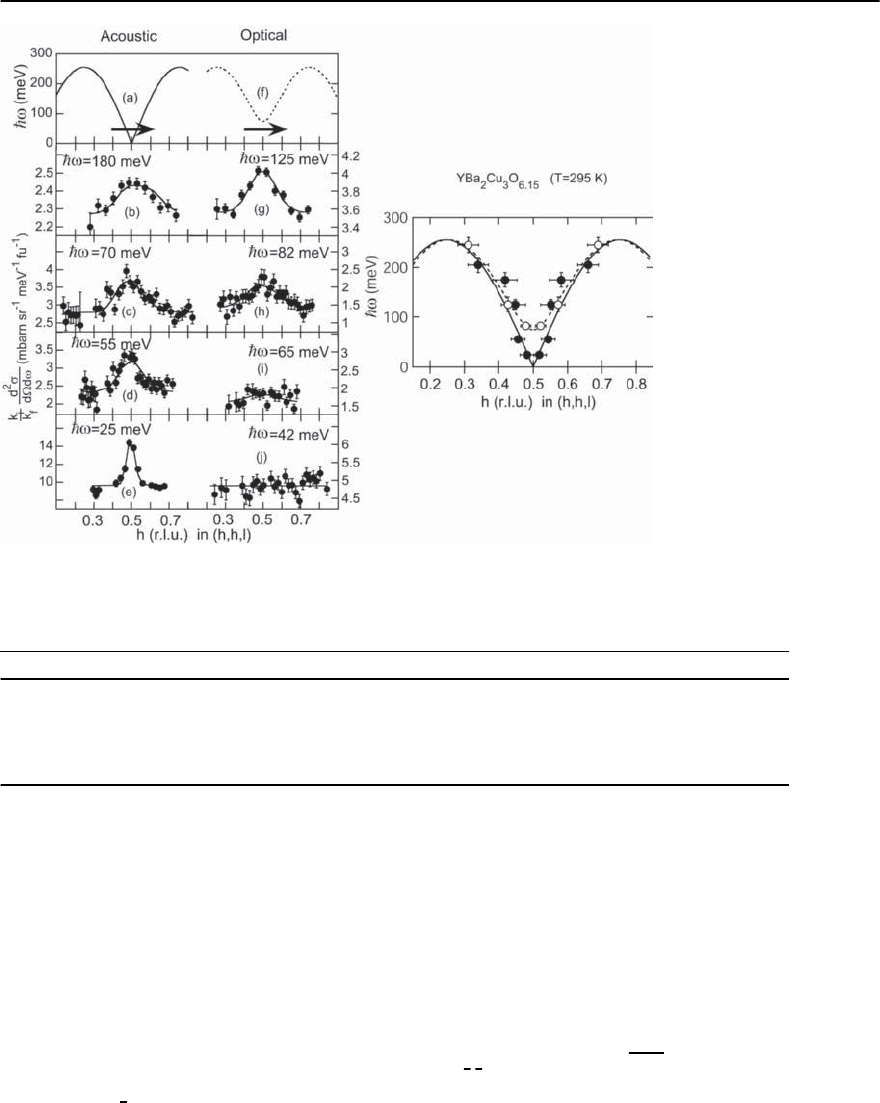
1014 S.M. Hayden

Fig. 18.24. Left:Constant

energy scans showing the

spin waves in YBa

6.15

Scans (b)–(e) are chosen

to emphasize the acous-

tic mode and scans (g)–

(i) to emphasize the op-

tical mode. The onset of

scattering for the optical

(even) mode is at about 74

meV. Right: The spin wave

dispersion in YBa

6.15

acoustic branch (closed cir-

cles, solid line),optic branch

(open circles, dashed line).

(After Hayden et al.) [116]

Table 18.3. Experimentally determined exchange constants for antiferromagnetic YBa

6+x

. No corrections have been

made for the effect of quantum ﬂuctuations which are expected to renormalise the bare exchange constants J

∗

= Z

with Z

≈ 1.18 (see Sect. 18.6.2).

Composition Ref. J

∗



(meV) J

∗

⊥

(meV) Z

!

(meV)

YBa

6.2

[114] 120 ± 20 > 8

YBa

6.2

[115] 10 67 ±5

YBa

6.15

[116] 125 ± 511±20.4 ± 0.174±5

PrBa

6.2

[117] 127 ± 10

respectively. The dispersion relations are

!

odd

(Q)=2Z



1−

(Q)

+ J

⊥





1+ (Q)

>

1/2

!

even

(Q)=2Z



1−

(Q)

+ J

⊥





1− (Q)

>

1/2

, (18.25)

where  (Q)=

[cos(2h)+cos(2k)] and z=3.2Å

is the separation of the CuO

planes in a bilayer.

The inter-planar coupling term in Eq. 18.22 leads

to no additional dispersion along the z-direction,

only a modulation in the amplitude of the response

which nevertheless can be used to distinguish be-

tween the two modes. Thus the bilayer nature of this

YBa

6+x

results in two collective modes with

additional structure to 



(q, !)ascomparedwith

the single layer material. The even or optic mode

has a gap at the 2D magnetic zone centres such as

(

l)of!



∗

⊥

∗



. Its intensity displays an

overall modulation cos

(zl/c) which has max-

ima at positions l =0, 3.7, 7.3,.... Correspondingly,

18 Neutron Scattering and the Magnetic Response of Superconductors 1015

the even or acoustic mode has an overall modulation

of sin

(zl/c) and therefore has maxima at l =

1.8, 5.5,....

There have been several studies of the spin

waves in strongly underdoped antiferromagnetic

YBa

6+x

[6,113–116]. Measurements made with

thermal neutronsat a reactor source by Shamoto and

co-workers [114] were able to resolve the acoustic

branches of the spin waves and estimate an exchange

constant coupling ofJ

∗



=120±20 meV.Higher energy

measurements were carried out by Reznik et al.[115]

and Hayden et al. [116] using hot neutrons at a reac-

tor source and spallation neutrons, they were able to

observe gaps in the optic (even) excitations of 67 ±5

meV and 74 ±5 respectively. Hayden et al.[116] also

showed that the magnetic excitations persisted up

to 275 meV and that the intensity of the spin wave

excitations is strongly renormalised due to quantum

ﬂuctuations (see Sect. 18.6.2) with Z

=0.4 ± 0.1.

18.6.3 Magnetic Excitations in La

2−x

CuO

Sr or Ba doping of La

CuO

causes the long range

antiferromagnetic Neel order to be replaced with a

frozen spin state at low temperatures. As discussed

above, this state has some of the characteristics of

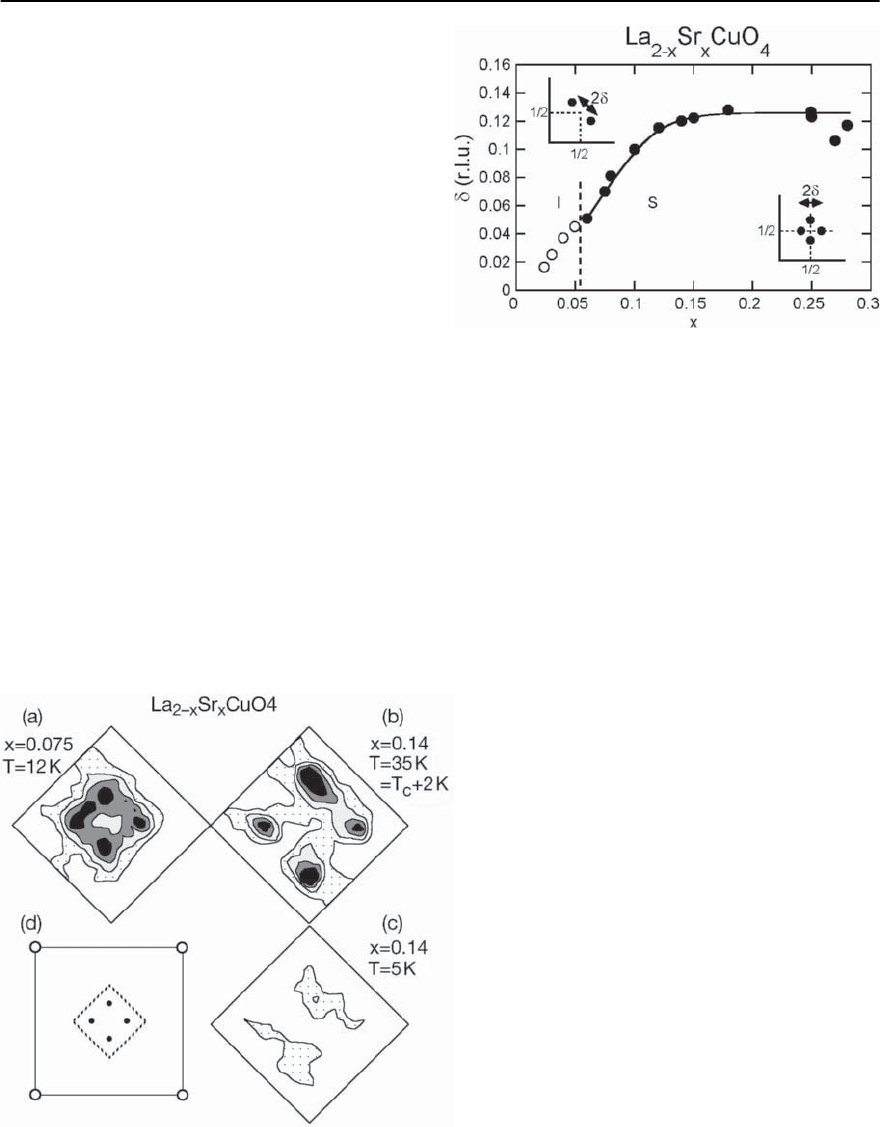
Fig. 18.25. The doping dependence of the incommensu-

rability ı of the low frequency magnetic excitations in

2−x

CuO

. Closed circles refer to the superconducting

or metallic state. Open circles refer to the incommensurate

order observed for lightly doped insulating compositions.

Data collected from [57,69,119,120]

a spin glass and is suppressed by optimal doping.

Thurston et al. [118] found that the low energy mag-

netic response of La

2−x

CuO

showed incommen-

surate peaks at finite frequencies near the (1/2,1/2)

position. The location of these peaks was identified

as (1/2 ± ı, 1/2) and (1/2, 1/2 ± ı)byCheonget

al. [119] for samples with x =0.075 and x =0.14.

Fig. 18.26. Low energy magnetic excitations in

2−x

CuO

.(a) x =0.075 and ! =1meVand

T = 12 K (after Cheong et al. [119]). (b)–(c) x =0.14

and ! =2meVforT above (b) and below T

(c). No-

tice how superconductivity suppresses the low energy

response

1016 S.M. Hayden

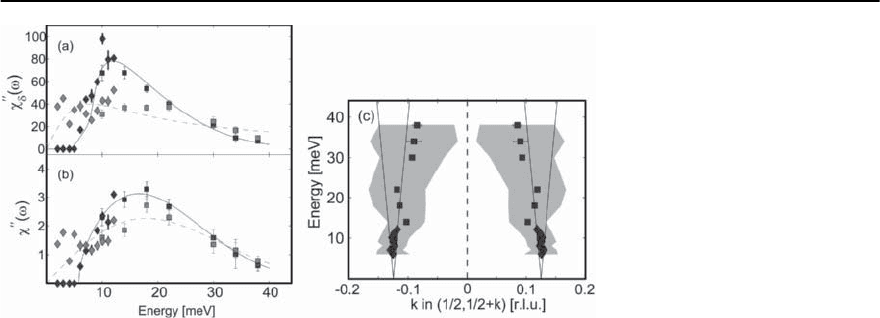
Fig. 18.27. Measurements of the low energy incommensurate magnetic excitations in La

1.84

0.16

CuO

.(a)Energyde-

pendence of 



(!), the fitted peak intensity of 



(q, !) at the incommensurate peak position Q

. Superconducting

phase, filled symbols; normal phase, open symbols. MAPS data, squares; triple-axis data, diamonds.(b) Local suscepti-

bility 



(!). (c) Dispersion of the excitations in LSCO. Shaded regions represent the fitted FWHM. Solid lines show the

spin-wave velocity of La

CuO

with J

∗

= 156 meV. Open circle: YBCO6.6. (After N.B. Christensen et al.[124])

The variationof the incommensuratewavevector has

been studied systematically with doping by Yamada

and co-workers [57,69,120]. The incommensurabil-

ity increases up to about ı =0.12 and then satu-

rates (see Fig. 18.25). The incommensurate ﬂuctua-

tions condense out near the x =1/8composition

to give incommensurate static order. This coincides

with a plateau in T

versus doping in La

2−x

CuO

and a marked dip in T

(x)inLa

2−x

CuO

.Another

interesting featureof the low-energy spin excitations

is that they are strongly temperature dependent. As

the temperature is lowered towards T

the intensity

of the low-energy incommensurate peaks increases

and the width in wavevector decreases [121]. Thus

it is clear that the incommensurate ﬂuctuations are

close to condensing and that they can be made to

condense near the x =1/8composition.Tranquada

et al. [73] have demonstrated that superconductiv-

ity can be completely destroyed and incommensu-

rate static spin and charge density waves induced

by substituting Nd for La in La

1.6−x

0.4

CuO

However it should be noted that this composition

has a different crystallographic structure to LTO

structure of La

2−x

CuO

. The low energy incom-

mensurate excitationsin La

2−x

(Ba,Sr)

CuO

broaden

and disperse with increasing energy [122–124]. Fig-

ure 18.27 shows the recent data of Christensen et

al. [124] which clearly demonstrate inward disper-

sion towards (1/2,1/2).

High Energy Response

The high-energy magnetic response in La

2−x

CuO

near optimal doping has been studied by spallation

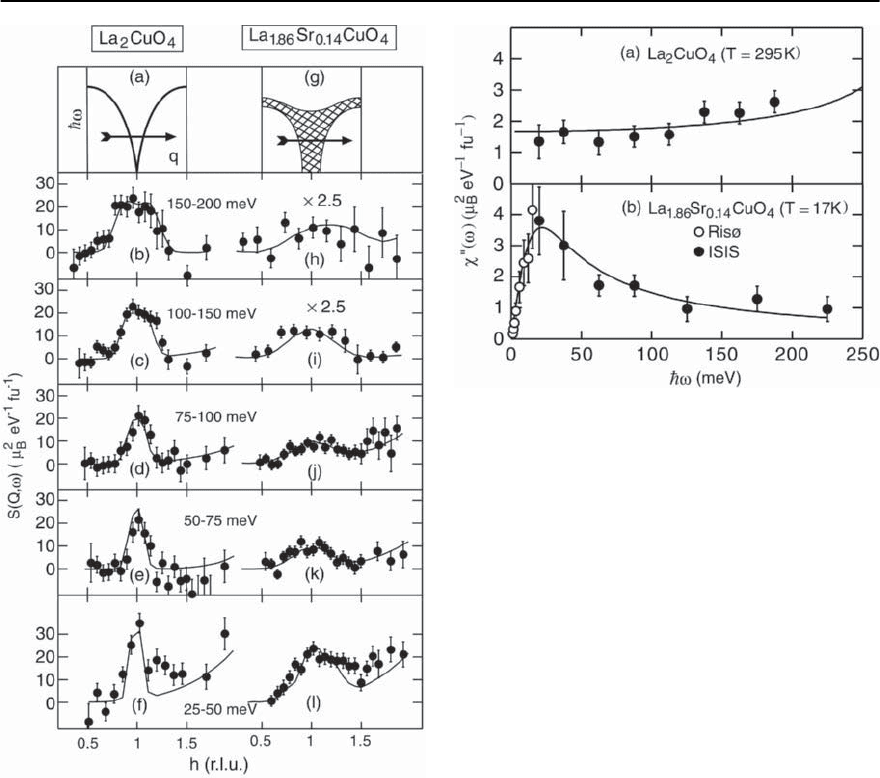
neutrons [125]: some of the results of this study are

shown in Figs. 18.28 and 18.29. It is found that mag-

netic excitationspersist up to 200–300meV,although

they are much weaker and broader in Q-space than

for the parent insulator La

CuO

. Surprisingly the

lower energy excitations are stronger in the super-

conductor than the insulator when the response is

integrated over wavevector to yield the local suscep-

tibility 



(!). Thus the characteristic energy scale

of the spin ﬂuctuations is lowered by doping (at least

up to x ≈ 0.14).

Superconducting State

Clearly we would expect the low energy magnetic

response to be suppressed on entering the super-

conducting state as other techniques such as NMR

which probe the spin susceptibility in the supercon-

ducting state show a strong reduction. Early work

on La

2−x

CuO

showed that the suppression of the

18 Neutron Scattering and the Magnetic Response of Superconductors 1017

Fig. 18.28. A comparison of the magnetic excitations in in-

sulating antiferromagnetic La

CuO

and superconducting

1.86

0.14

CuO

. (After Hayden et al. [125])

magnetic response in the superconducting state is

dependent on sample quality [119,126–130]. In clean

samples, a suppression of the magnetic response is

observed below about 7 meV for samples near op-

timal doping [124,127–130] with the lower energy

incommensurate excitations being completely sup-

pressed within the experimental error.At higher en-

ergies the incommensurate magnetic response is en-

hanced on entering the superconducting state [124,

129, 130]. Entering the superconducting state also

causes the magnetic response to become sharper in

Fig. 18.29. The local susceptibility for insulating antiferro-

magnetic La

CuO

and superconducting La

1.86

0.14

CuO

Doping leads to a suppression of the integrated spectral

weight at higher energies.However,the integrated response

at lower energies, ! ≈ 15 meV, is larger in the supercon-

ductor than the insulator. (After Hayden et al.[125])

wavevector [129,130]. For optimally doped samples

the greatest enhancement occurs at about 15 meV

[124]. Fig. 18.27 shows data from Christensen et al.

[124] illustrating these effects.

18.6.4 Magnetic Excitations in YBa

6+x

The bilayer structure of YBa

6+x

complicates

both the measurement and interpretation of the spin

excitations with respect to the La

2−x

CuO

system.

Asdiscussedin Sect.18.6.2,the bilayer structureleads

to two types of magnetic excitation (odd and even) in

which corresponding spins in neighbouring bilayers

precess in-phase or out-of-phase. Separating the two

types of excitation requires the choice of particular

components of momentum parallel to c

∗

(l values).

This places kinematic constrains on the scattering

experiment.

The most obvious feature of the magnetic re-

sponse in YBa

6+x

is the so-called resonance

peak [10,132,133] in 



(q, !) which occurs at Q

(1/2,1/2) in the odd channel and at an energy of

41 meV for optimal doping. The resonance develops

near T

at optimally doping [10,133]. Figure 18.30

1018 S.M. Hayden

Fig. 18.30. The magnetic response 



(Q, !)inthenormal

(open squares) and superconducting (closed circles) state

in YBa

6.92

. (After Bourges et al.[131])

shows the resonance for optimal doping. For under-

doped compositions a peak in 



(q, !)asafunction

of ! develops at the resonance energy above T

.This

peak becomes sharper and more intense as the tem-

perature is lowered through T

[79,80]. Fig. 18.31

shows data on underdoped YBa

6.6

illustrating

these points.The resonance has recently been studied

in highly underdoped [82,84] and overdoped [134]

samples. The energy of the (odd) resonance appears

to approximately track T

,withE

res

≈ 5.1kT

as il-

lustrated in Fig. 18.38.

Fig. 18.32. The incommensurate response in YBa

6.6

for energies below the resonance (After Mook et al.[135])

It is now clear that the “resonance” is the most

intense part of a mode which disperses downwards

away from (1/2,1/2). The first evidence for the ex-

istence of such a mode was the observation of an

incommensurate structure in wavevector for ener-

gies below the resonance energy [135,136]. Figure

18.32 shows incommensurate scattering measured at

! = 24 meV for underdoped YBa

6.6

.There

have been several proposals [137–141] for the form

of the dispersion of the resonance mode. Figures

18.33 and 18.34 show early proposals from Arai et

al. [137] and Bourges et al. [138]. There is some de-

bate about the existence of a weaker upward dispers-

ing mode reported by some groups [139,140] but

not others [141]. Figure 18.35 shows an image of the

resonance mode in YBa

6.6

[141]. The incom-

Fig. 18.31.The odd and even components of the local susceptibility for YBa

6.6

(After Dai et al. [80])