Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors
Подождите немного. Документ загружается.


18 Neutron Scattering and the Magnetic Response of Superconductors 999
18.2.7 The Moment Sum Rule and the
Fluctuation-DissipationTheorem
The best known example of the fluctuation-
dissipation theorem (FDT) is probably Brownian
motion. In a colloidal suspension, the particles
move about randomly because they are bombarded
by molecules in the liquid. If these particles were
charged and we attempt to move them with an exter-
nal field, then impacts of the molecules would cause
the charged particles to experience a resistive force
which is proportional to their velocity. The same
mechanism (bombardment by molecules) is respon-
sible for both the random fluctuations in position
and the response to an external field. The relation-
ship between the response of a system and (thermal
or quantum) fluctuations within the system is gov-
erned by a fluctuation-dissipation theorem [12].Here
we consider only the magnetic case in which the fluc-
tuations are in the magnetization M(r, t)andtheex-
ternal field is the magnetic field H(r, t). In this case,
the unsymmetrised fluctuation-dissipation theorem
(FDT) is [7],
∞
−∞
dte
−i!t
9
M
(Q, t) M
(−Q, 0)
:
=2V
(Q, !)
1−e
−ˇ!
. (18.11)
The unsymmetrised form of the FDT is most rele-
vant to scattering experiments because the scattering
cross-section is typically related to the left hand side
of Eq. 18.11. If we integrate Eq. 18.11 with respect to
frequency and wavevector and assume the system is
isotropic,weobtaina moment sumrulefor
(Q, !):
9
M
2
:
=
M
2
x
+ M
2
y
+ M
2
z
=
BZ
dQ
×
∞
−∞
[
xx
(Q, !)+
yy
(Q, !)+
zz
(Q, !)] d!
1−exp(−!/kT)
=
3
BZ
dQ
∞
−∞
(Q, !)d!
1−exp(−!/kT)
. (18.12)
We can compare the total moment obtained from the
moment sum rule with the atomic moment of the
constituent ions. For an ion with spin-only moment,
we would expect the total moment to be,
9
M
2
:
= g
2
2
B
S(S +1)
=3
2
B
for S =
1
2
, g =2.
18.3 The Static Spin Susceptibility of
Superconductors
The static spin susceptibility
spin
=
spin
(Q =
0, ! = 0) can provide very useful information about
the nature of the superconducting state. In a con-
ventional superconductor with spin-singlet pairing,
the spin susceptibility is suppressed on entering the
superconducting statebecausespins pair up.Thesin-
glet pairs have a total spin S = 0 and therefore do not
respond to an external magnetic field. For B B
c2
,
the temperature dependence of
spin
(T) is described
by theYosida function[13],thisfunctionis plottedin
Fig. 18.5(a). The spin susceptibility cannot be mea-
sured directly using a magnetometer in the super-
conducting state because diamagnetic supercurrents
flow on the surface of the superconductor when a
field is applied and screen out the response. How-
ever, magnetic neutron scattering and NMR (knight
shift) do not suffer from this limitation. The mea-
surement of
spin
using neutrons is an interesting
application of the interference between the magnetic
and nuclear cross sections. Neutrons interact with
condensed matter both through the strong nuclear
interactionand through the electromagnetic interac-
tion.If we satisfy the Bragg condition,then scattering
occurs both because of the periodicity of the nuclear
density andbecauseof themicroscopic periodicity of
the magnetization density. The two scattered waves
interfere. The sign of interference term depends on
the relative orientation of the neutron spin and the
sample magnetization. Thus, it may be isolated from
other scattering by reversing the spin polarization
of a spin-polarized neutron beam. Shull and Wedg-
wood [14] used this method to determine the suscep-
tibility of the conventional superconductor V
3
Si in
the superconducting and normal states.Their results
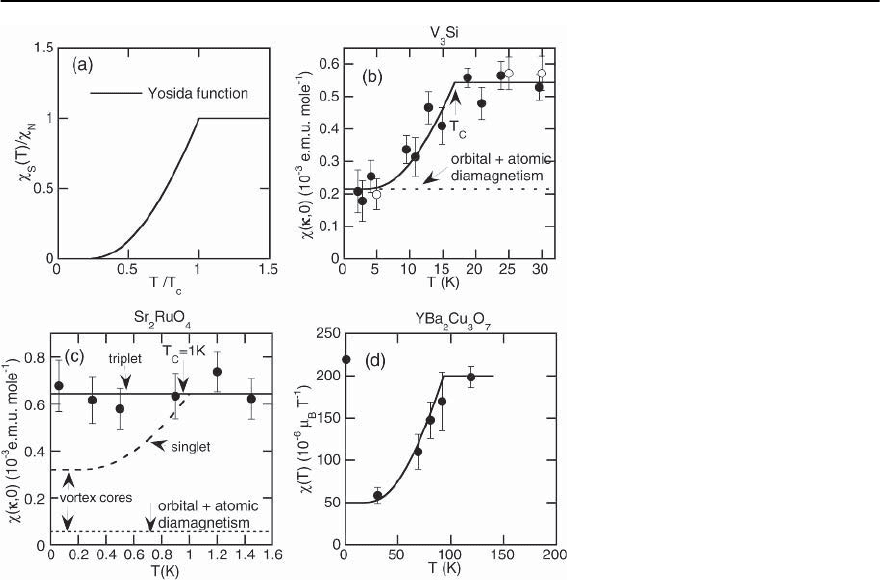
1000 S.M. Hayden
Fig. 18.5. (a) The spin susceptibility of
a singlet superconductor (Yosida func-
tion) [13]. (b) The magnetic suscepti-
bility of V
3
Si, a conventional singlet su-
perconductor measured in the super-
conducting state using polarized neu-
trons [14].(c) Susceptibility of Sr
2
RuO
4
,
believed to be a triplet-paired p-wave
superconductor [15]. (d) Susceptibility
of YBa
2
Cu
3
O
7
, a singlet-paired d-wave
superconductor [16]
are shown in Fig. 18.5(b). Shull and Wedgwood ob-
served a drop of the susceptibility through T
c
which
was consistent with the Yosida function. However,
their experiment also demonstrated that the orbital
susceptibility remained finite as T → 0. 3d tran-
sition metal compounds such as V
3
Si have an or-
bital (van-Vleck) susceptibility which is comparable
to their spin susceptibility.
Having discussed the case of a conventional spin-
singlet superconductor, we now consider the case of
triplet-paired (or odd-parity) superconductors. It is
widely believed that Sr
2
RuO
4
is such a system [17].
The pairing in triplet or odd-parity superconduc-
tors is somewhat more complicated than the singlet
case because there are many possible triplet states.
Rice and Sigrist [18] andBaskaran [19] proposed that
Sr
2
RuO
4
formed a state analogous to the “equal-spin
pairing” (ESP) state of
3
He discussed by Anderson
and Morel [20]. Within an EPS scenario the super-
conducting state is a superposition of the two possi-
ble (S = 1) parallel paired states. In an applied mag-
netic field, the Cooper pairs are simultaneously re-
sponsible for the superconductivity and the induced
magnetization through the differing occupation of
the S
z
= ±1 states, leading to the same susceptibil-
ity as the normal state. Duffy and co-workers [15]
used the polarized-beam measurements of the in-
duced form factor to determine (T)forSr
2
RuO
4
.
Figure 18.5(c) shows (T) for Sr
2
RuO
4
measured
through the superconducting transition. On enter-
ing the superconductingstate we find that there is no
change in , supporting the notion that Sr
2
RuO
4
has
an EPS-type triplet paired state. Similar polarized-
neutron experiments have been performed on the
heavy-fermionsuperconductorsUPt
3
andUBe
13
[21]
whichalso show no reductionin the spinsusceptibil-
ity on entering the superconducting state suggesting
that they too have odd-parity pairing. For complete-
ness we note that complementary informationis ob-
tained from NMR Knight shift measurements which
show no change in the spin susceptibility at T
c
in
UPt
3
or UBe
13
.
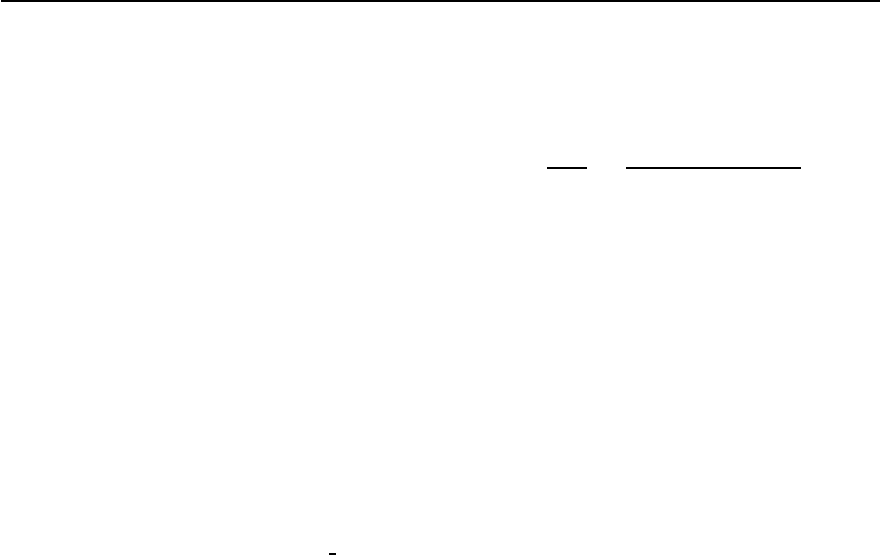
18 Neutron Scattering and the Magnetic Response of Superconductors 1001
Finally we discuss the case of the high-T
c
super-
conductors whichare generallybelievedto be d-wave
with singlet spin pairing. In common with conven-
tional s-wave singlet pairing, we expect (T) to fol-
low aYosida function.The complication with high-T
c
materials is that the spin susceptibility can begin to
drop at high temperatures because of the formation
of the so-called “pseudo-gap”. This is particularly
the case for underdoped compositions. Nevertheless,
the slightly overdoped YBa
2
Cu
3
O
7
sample studied by
Boucherle and co-workers [16] shows a drop in (T)
which is consistent with a Yosida function.
18.4 Magnetic Excitations in Metals and
Weakly Coupled Superconductors
In this review we will discuss the magnetic excita-
tions in conventional and more exotic superconduc-
tors such as the high-T
c
materials. The purpose of
this section is to introduce the theory of magnetic
excitations in single-band weakly-correlated metals.
We will consider the excitations of S =
1
2
insulating
antiferromagnets in Sect. 18.6.2. Both limits are rele-
vant to the high-T
c
materials where the parent com-
pounds are antiferromagnets and overdoped materi-
als show many of the properties of Fermi liquids. Of
course, even in their normal state, optimally doped
cuprates show anomalous properties and the elec-
tronic state is not well described by conventional
one-electron theory. Nevertheless the next sections
should provide some basis to qualitatively under-
stand the cuprates and other superconductors.
18.4.1 Paramagnetic Metals
In metals with weak magnetic correlations such as
sodium, the magnetic excitations are “electron-hole
pairs”. A magnetic field varying in space and time
(such as that produced by a neutron moving through
a sample) can excite electrons from below the Fermi
energy to unoccupied states above it. This process
creates an“electron-hole pair”or“Stoner”excitation.
Inthecaseofthesodium,thelargebandwidthand
weak exchange interaction mean that the electron-
hole excitations are spread out over several eV in
energy.This makes them difficult to observe directly.
The response of a paramagnetic metal due to the
electron-hole excitations is given by the so-called
Lindhard functions [7,8,22],
0
(q, !)
=
g
2
2
B
4N
k
f (
k+q
)−f (
k
)
! −(
k+q
−
k
)+i
, (18.13)
(k) is the band energy, f (E) the Fermi–Dirac func-
tion and there is no sum over spin states.
The Lindhard response function describes a con-
tinuum of electron-hole excitations. For small en-
ergy transfers the response can be related to elec-
tron states near the Fermi energy (cf. Eq. 18.13)
and may therefore reflect the Fermi surface. The
response can be strong in materials with highly
nested Fermi surfaces or with an exchange interac-
tion which favours (but does not result in) magnetic
order. An example of the former is the Cr
1−x
V
x
alloy
system [23–25]. Chromium is an incommensurate
antiferromagnet with a strongly nested Fermi sur-
face. The antiferromagnetism may be destroyed by
alloying with V, producing a highly-nested paramag-
netic metal. Fawcett et al. [24] demonstrated the ex-
istence of strong overdamped excitations at incom-
mensurate positions in the paramagnet Cr
0.95
V
0.05
,
which have similarities to the low-frequency exci-
tations in La
2−x
Sr
x
CuO
4
. These “spin-density-wave
paramagnons”, as they were named, exist up to at
least 400 meV [25].
18.4.2 The Superconducting Metal
One of the achievements of the BCS theory of super-
conductivity was to demonstrate that when a metal
becomes superconducting, correlations are intro-
duced between the motionof the electrons.In a“con-
ventional” singlet s-wave superconductor, Cooper
pairs are formed such that the states |k ↑> and
|−k ↓> are simultaneously occupied. Since the spin
susceptibility also measures correlations between
electrons, it is not surprising that the formation of
the superconducting state can dramatically effect
(q, !).In conventionalsuperconductors,thesmall
value of the superconducting gap has precluded di-
rect measurements of changes in
(q, !)usingin-
elastic neutron scattering. However, measurements
1002 S.M. Hayden
of the spin susceptibility in the superconducting
state have been made by other means. For exam-
ple, nuclear magnetic resonance (NMR) measured
the low-frequency local susceptibility and yielded
the celebrated “Hebel–Slichter peak” [26]. BCS the-
ory makes definite predictions for the magnetic re-
sponse [27,28] (atleast in a simple metal).Wemust ef-
fectively evaluate a Lindhard function for the super-
conductor. In the superconducting state, the quasi-
particle excitation spectrum is given by,
E
2
k
=
k
−
2
+ |
k
|
2
, (18.14)
where (k) is the electron energy in the normal state
and is the chemical potential. For a conventional
s-wave superconductor the gap, (k)isnon-zero
and k-independent. The existence of the BCS pair-
ing means that the |k ↑> and |−k ↓> states are
coupled, this introduces “coherence factors”into the
Lindhard expression. In the superconducting state,
the magnetic response is given by [27,28],
0
(q, !)=
g
2
2
B
4N
×
k
1
2
1+
k+q
k
+
k+q
k
E
k+q
E
k
×
f (E
k+q
)−f (E
k
)
! −(E
k+q
− E
k
)+i
+
1
4
1−
k+q
k
+
k+q
k
E
k+q
E
k
×
1−f (E
k+q
)−f (E
k
)
! +(E
k+q
+ E
k
)+i
+
1
4
1−
k+q
k
+
k+q
k
E
k+q
E
k
×
f (E
k+q
)+f (E
k
)−1
! −(E
k+q
+ E
k
)+i
, (18.15)
Fig. 18.6. Calculation of the bareLindhard susceptibility
0
(q, !)with! = 35 meV for a 2D one-band tight-
binding model with parameters used by Norman [35]
and a d-wave superconducting gap
0
=35meV
Fig. 18.7. The effect of superconductiv-
ity on the magnetic response
0
(q, !)
of a simple metal illustrated through
the calculation of the Lindhard func-
tions with the BCS coherence factors
(Eq. 18.15). Parameters as in Fig. 18.6.
An s-wave gap leads to a suppression
of the response below 2,whilead-
wave gap can lead to an enhancement of
the response for energies near 2.(left
panel) q =(1/2, 1/2), (right panel)
q =(1/2, 1/2) and (1/2, 1/2+ı)
18 Neutron Scattering and the Magnetic Response of Superconductors 1003
where
k
=
k
− . The three terms correspond
to quasiparticle scattering, quasiparticle pair an-
nihilation and quasiparticle pair creation. In the
limit of zero temperature, only the final term con-
tributes to the response. Unfortunately, Eq. 18.15 ne-
glects electron–electron interactions which are un-
doubtedly very important in the cuprates and many
other types of superconductor. It implicity assumes
that there are no exchange interactions. More com-
plete models have been investigated in the litera-
ture [28–38]. Despite the approximations inherent
in Eq. 18.15, it may still give some qualitative indica-
tionsof howthemagnetic responsechangeson enter-
ing the superconducting state. Figures 18.6 and 18.7
show a model calculation of
(q, !)basedona2D
one-band tight-binding model with parameters [35]
reputed to describe the cuprates. The model quali-
tatively reproduces the four incommensurate peaks
located around the (1/2,1/2) position which are ob-
served in La
2−x
Sr
x
CuO
4
andYBa
2
Cu
3
O
6+x
.The effect
of the superconductivity on the magnetic response
is illustrated in Fig. 18.7. The panels shows the en-
ergy dependence of
(q, !) at the peak positions
in Fig. 18.6 and at (1/2,1/2). For an s-wave gap, there
is a complete suppression of
(q, !) for ! < 2.
In the d-wave singlet case, there is a q-dependent
suppression at lower energies and an increase in
(q, !) for some wavevectors near ! ≈ 2.
18.5 Excitations and Superconductive
Pairing
One of the remarkable successes of the BCS the-
ory of superconductivity was the identification of
the pairing mechanism. Within the BCS framework
the exchange of virtual Bosonic excitations causes
an attractive interaction between itinerant electrons
which then pair up. In “conventional” superconduc-
tors such as Pb and Nb, the Bosonic excitations
were identified as phonons and the pairing is in
the s-wave channel. Neutron scattering and tun-
nelling measurements demonstrated the pairing bo-
son in lead very directly. Superconductor-insulator-
superconductor (SIS) tunnelling measurements al-
low the energy-dependent spectrum of the bosons
which mediate the pairing to be extracted [41]. Fig-
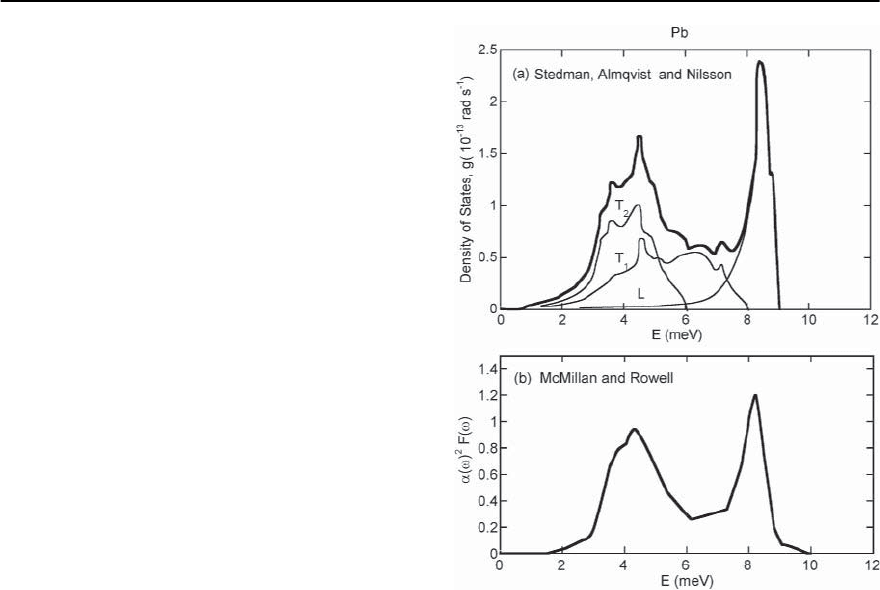
Fig. 18.8. (a) Thedensity of phonon states determined from
neutron scattering (after Stedman et al. [40]). In this ex-
periment the phonon DOS was determined from the entire
measured phonon dispersion for each phonon polariza-
tion. T1 and T2 are transverse modes, L is longitudinal.
(b) The product of the electron–boson coupling and the
boson DOS, ˛
2
(!)F(!) determined from SIS tunnelling
measurements (after McMillan and Rowell [41]). Note the
similarity between the total phonon DOS and ˛
2
(!)F(!),
showing that both transverse and longitudinal phonons
are involved in pairing
ure 18.8(b) shows the experimentally determined
˛
2
(!)F(!) for lead [41] (˛
2
(!)isameasureof
the electron–boson coupling and F(!)istheboson
density of states). Figure 18.8(a) shows the phonon
density of states determined from neutron scatter-
ing [40]. Comparing panels (a) and (b), one can im-
mediately see that the total phonon density of states
is reflected in ˛
2
(!)F(!) identifying phonons as the
mediating bosons. The neutron scattering measure-
ments were even able to determine the contributions
of the differentphonon polarizations to the total DOS
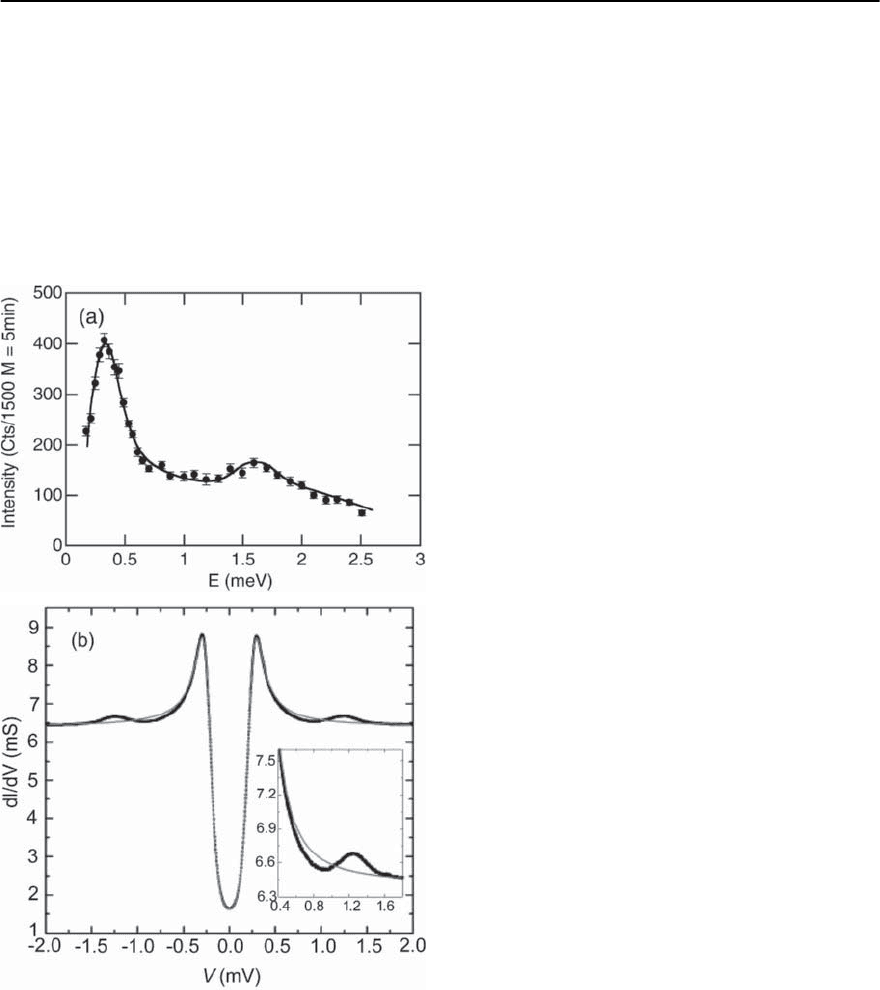
1004 S.M. Hayden
(see Fig. 18.8(a)). Since the peaks due to the lon-
gitudinal (L) and transverse (T) phonons occur in
˛
2
(!)F(!), both polarizations must contribute to
the superconductive pairing.
The antiferromagnetic (T
N
=14.3K)heavy-
fermion superconductor UPd
2
Al
3
is an interesting
compound because it shows a strong correspon-
dence between its magnetic excitations and the
tunnelling density of states. Dispersive crystal-field
excitations (magnetic excitons) were observed by
Fig. 18.9. (a) Magnetic excitations in UPd
2
Al
3
measured by
neutron scattering (after Bernhoeft et al. [44]). Data were
collected near the antiferromagnetic ordering wavevec-
tor Q = (0,0,1/2) in the superconducting state (T=0.15 K).
(b) Tunnelling DOS measured in a UPd
2
Al
3
-AlO
x
-Pb tun-
nel junction (after Jourdan et al. [45])
Petersen and co-workers [42] in INS experiments
within the antiferromagnetic(AF) phase of UPd
2
Al
3
.
Laterhigher-resolutionexperiments[43,44]revealed
that a double-peak structure appears in the magnetic
excitation spectrum below T
c
=1.8K,withpeakpo-
sitions at E ≈ 0.35 and 1.7 meV (see Fig. 18.9). The
lower peak reduces with increasing temperature, and
becomes a “quasielastic line” (that is, with spectral
line-shape centred around E = 0). This dramatic re-
distribution of spectral weight as we pass through
T
c
suggests that the lower peak is associated with
the itinerant heavy quasiparticles.The higher-energy
peak shows considerable dispersion in wavevector
on moving away from the from the antiferromag-
netic zone centre, it has therefore been associated
with a collective mode of the localized-5f moment
system due to the inter-site interactions. Thus the
INS results demonstrate that a strong interaction ex-
ists between the localized and delocalized compo-
nents of the 5f -electron system. The tunnelling den-
sity of states of UPd
2
Al
3
was measured by Jourdan
and co-workers [45] using UPd
2
Al
3
-AlO
x
-Pb tunnel
junctions. Interestingly, strong-coupling features ap-
pear in the tunnelling DOS around 1.2 meV and a
2 peak appears near 0.3 meV. The neutron scatter-
ing and tunnelling together suggest that the bosons
responsible for the superconductive pairing of the
itinerant electrons in UPd
2
Al
3
are the magnetic ex-
citons. This scenario has been analyzed by Sato and
co-workers [46] who were able to explain qualitative
features of the magnetic excitation and the super-
conducting tunnelling spectra.
18.6 High Temperature Superconductivity
High temperaturesuperconductivity in CuO
2
layered
cuprates was first discovered in La
2−x
Ba
x
CuO
4
[47].
Since this time, the phase diagram of this and other
cuprates have since been explored in considerable
detail (see, for example, the article by H.R. Ott in
this series). A very schematic generic phase dia-
gram is shown in Fig. 18.10. Soon after the orig-
inal discovery of the high-T
c
phenomenon, neu-
tron scattering experiments performed by Vaknin
et al. [48] demonstrated that the “undoped” par-
ent compound La
2
CuO
4
was antiferromagnetic. The
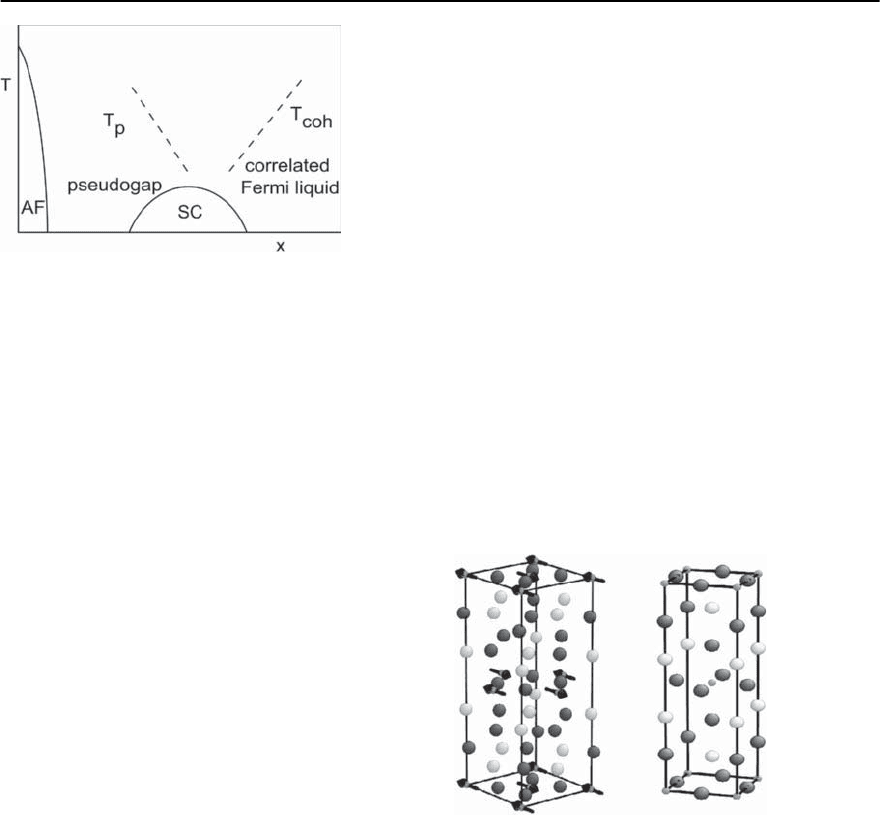
18 Neutron Scattering and the Magnetic Response of Superconductors 1005
Fig. 18.10. The generic phase diagram of the cuprate super-
conductors
overdoped cuprates are strongly correlated (non-
superconducting) metals which show a T
2
tempera-
ture dependence in their resistivity [49] and evidence
of a Fermi surface [50]. The superconductivity oc-
curs between these two regions and on phenological
grounds should share some features with these other
phases. In the next sections we review the magnetic
excitations inthe parent insulatingantiferromagnets
La
2
CuO
4
andYBa
2
Cu
3
O
6
.We will see in later sections
that the magnetic excitations in the superconducting
compositionsshow residual antiferromagnetic inter-
actions.Thus,studies of the parent antiferromagnets
afford an understanding of the underlying magnetic
interactions.
For completeness we briefly mention the so-called
pseudogap, a phenomenon which occurs in the un-
derdoped region of the phase diagram. In the years
following the discovery of high-T
c
superconductors,
it was found that the superconductivity had a large
energy scale 2
∗
associated with it. Its importance
was slowly recognized through the 1990s and it has
become known as the “pseudogap” (see reviews by
Timusk and Statt [51], and Tallon and Loram [52]).
The pseudogap is often associated with a tempera-
ture scale T
∗
below which its effects are felt.The pseu-
dogap was first observed in NMR experiments [53],
although it is visible in many types of measurement
(e.g.resistivity,infraredconductivity,Ramanscatter-
ing and tunnelling data).The“pseudogap”and its as-
sociated temperature T
∗
are largest for underdoped
compositions. Below T
c
it merges with the supercon-
ducting gap, but it is visible far above T
c
in many
spectroscopic measurements.
18.6.1 Structures and Phase Diagrams
In this short review, we will concentrate on the two
systems which have been studied most systematically
by neutron scattering. Relatively large single crystals
of YBa
2
Cu
3
O
6+x
and La
2−x
Sr
x
CuO
4
are available and
this is the primary reason why more data is available
for these systems.
Structure and Phase Diagram of La
2−x
Sr
x
CuO
4
The crystal structures observed in the La
2−x
Sr
x
CuO
4
system are shown in Fig. 18.11. At ambient tem-
perature La
2
CuO
4
is orthorhombic, due to a rota-
tion of the octahedra centred on the copper atoms.
La
2
CuO
4
becomes tetragonal for temperatures above
530 K [48, 54] and with doping La
2−x
Sr
x
CuO
4
be-
comes tetragonal for x > 0.21 [55,56]. For conve-
nience and to allow comparison between different
phases, we will generally use the tetragonal crys-
Fig. 18.11. Left: The low temperature orthorhombic (LTO)
phase of La
2
CuO
4
. The LTO phase is stable at low tempera-
tureforSrdopingx < 0.21. The LTO phase is described by
the Cmca (or isomorphic Bmab) space group [56]. In the
antiferromagnetic state, the ordered moments are stacked
in ferromagnetic sheets along [100] with the moments
pointing along the [001] direction [48]. Right :Athigh
temperatures and larger dopings the La
2−x
Sr
x
CuO
4
system
forms the high temperature tetragonal phase (HTT). The
HTT phase is described by the I4/mmm space group. To
allow comparison between different HTC systems, we label
reciprocal space using the tetragonal I4/mmm convention.
In this convention a = b ≈ 3.8Å,c ≈ 13.2 Å and [100] is
parallel to the Cu-O bond within the CuO
2
planes
1006 S.M. Hayden
tallographic axes to describe the high-T
c
cuprates
and their parents. The tetragonal (I4/mmm) crystal
structureofLa
2−x
Sr
x
CuO
4
isshown in the right hand
panel of Fig. 18.11. The electronic properties of the
La
2−x
(Ba,Sr)
x
CuO
4
system are extremely anisotropic.
Many properties are most easily understood by con-
sidering the structure as being made up of a series
of square CuO
2
planes stacked along the c direction.
There is weak overlap of the electronic orbitals in
the c direction. The copper atoms are in the Cu
2+
state with spin S =
1
2
. There is a strong exchange
anisotropy, the coupling between copper spins in the
same CuO
2
plane (J
) is several orders of magnitude
stronger than the coupling between spins in neigh-
bouring planes (J
⊥
).
As mentioned above, experiments performed by
Vaknin et al. [48] at Brookhaven National Labora-
tory showed that La
2
CuO
4
is an antiferromagnet
(see Fig. 18.11). The ordered moments point along
the tetragonal [110] or orthorhombic [001] direc-
tion [48]. A number of effects are known to change
the value from the 1
B
corresponding to S =
1
2
:(i)
the g factor of Cu
2+
[48]; (ii) covalency effects due
to hybridisation of the copper and oxygen atoms in
the planes [59,60]; (iii) variations due to oxygen sto-
ichiometry [61]; (iv) reduction due to the quantum
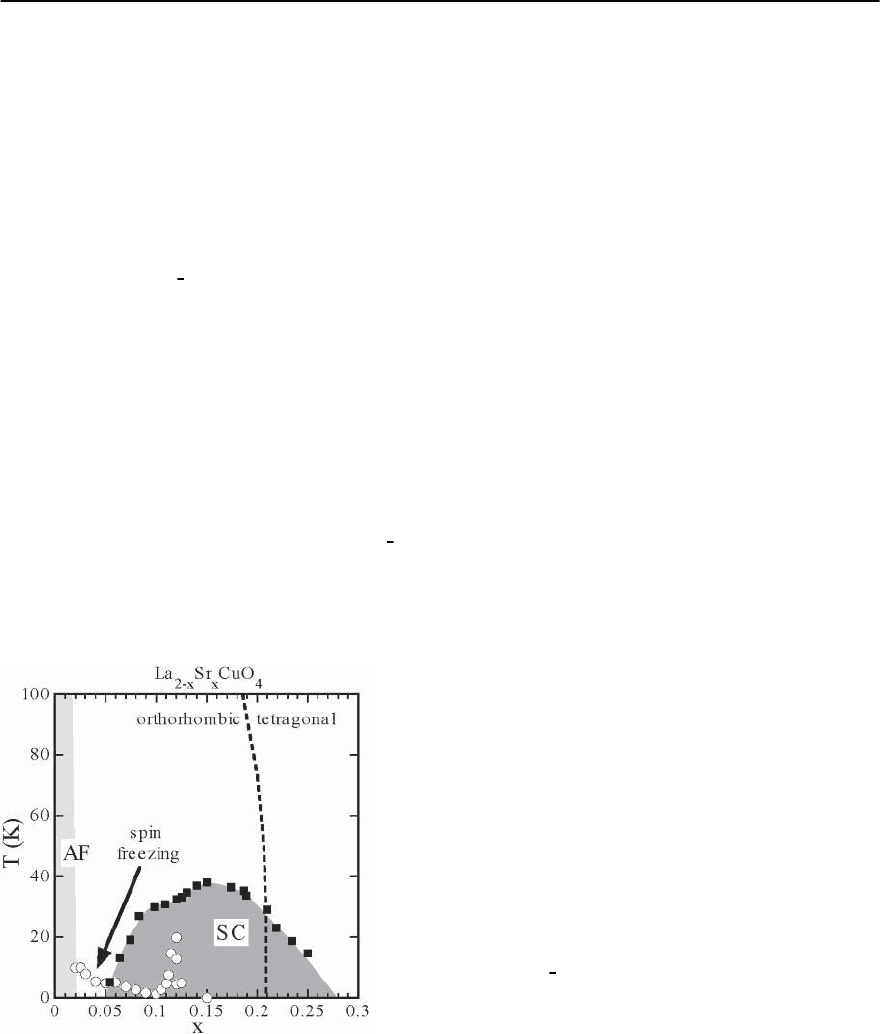
Fig. 18.12. The phase diagram of the La
2−x
Sr
x
CuO
4
system
showing the antiferromagnetic phase, superconductivity,
spin freezing and the orthorombic/tetragonal phase tran-
sition. Data collected from [57,58]
fluctuations expected in a low-dimensional antifer-
romagnet with small spin (see Sect. 18.6.2). Experi-
ments [48,61,62] have yielded ordered moments in
the range 0.3–0.6
B
.
LDA-bandstructure calculations [63] predict that
La
2
CuO
4
is a metal. In fact, correlation effects mean
that it is an antiferromagnetic Mott insulator.The ad-
dition of barium or strontium creates a plethora of
behaviour illustrated is Fig. 18.12.Theeffect of the Sr
or Ba is to add holes, moving the system away from
half filling and resulting in a transition to a metal-
lic and superconducting state for x ≈ 0.05. It is well
known that both the normal metal and the super-
conductor are anomalous in many ways. Although
the normal metal is characterized by an increasing
resistivity with temperature, the resistivity is several
orders of magnitude larger than for good metals.
Further, it shows a linear variation with tempera-
ture signalling an extremely temperature dependent
scattering mechanism.
Doping not only affects the electrical properties,
but also has dramatic effects on the magnetic ground
state. The long-range antiferromagnetic order is
rapidly destroyed with increasing x.Forx > 0.02,
the antiferromagnetism is replaced by short range
antiferromagnetic correlations at low temperatures.
This state appears to be formed by “spin freez-
ing” and has some analogies to the formation of a
spin glass. This “antiferromagnetic spin glass” has
been characterized both by local probes: SR [64],
NMR [65], M¨ossbauer [66] and by neutron scatter-
ing [67,68].Inthe lightly doped regime,neutronscat-
tering measurements on La
1.95
Ba
0.05
CuO
4
[67] have
studied the dynamics of the spin-freezing process.
Matsuda et al. [69] have made a systematic study
of the doping dependence of the freezing wavevec-
tor in the La
2−x
Sr
x
CuO
4
system (see Fig. 18.25). At
higher x, local probes indicate an enhanced island
of static order in the La
2−x
Sr
x
CuO
4
phase diagram
near x =
1
8
. Suzuki et al. [68] observed the cor-
responding incommensurate magnetic peaks. The
elastic incommensurate peaks are strongly enhanced
by an applied magnetic field [70–72]. Incommensu-
rate magnetic superlattice peaks have also been ob-
served in La
1.6−x
Nd
0.4
Sr
x
CuO
4
[73], although in this
case the material first undergoes a transition to a

18 Neutron Scattering and the Magnetic Response of Superconductors 1007
Fig. 18.13. Left:TheCuO
2
plane showing the atomic orbitals (Cu 3d
x
2
−y
2 and O 2p
x,y
) involved in the magnetic interactions.
J, J
and J
are the first-, second- and third-nearest-neighbour exchanges and J
c
is the cyclic interaction which couples
spinsatthecornersofasquareplaquette.Arrows indicate the spins of the valence electrons involved in the exchange.
Right: Reciprocal space for a 2D square antiferromagnet such as a single CuO
2
plane in La
2
CuO
4
. Solid circles denote
reciprocal lattice points. The open circle denotes the antiferromagnetic ordering wavevector
low-temperature tetragonal phase at higher temper-
atures.
Structure and Phase Diagram of YBa
2
Cu
3
O
6+x
TheYBa
2
Cu
3
O
6+x
system is probably the most widely
studied high-T
c
superconductor, primarily because
of its high-T
c
and the availability of largesingle crys-
tals. Figure 18.14 shows the unit cell of the antiferro-
magnetically ordered parent compound YBa
2
Cu
3
O
6
.
In common with many other high-T
c
systems, the
YBa
2
Cu
3
O
6+x
system has pairs of CuO
2
planes which
Fig. 18.14. The tetragonal unit cell of antiferromagnetic
YBa
2
Cu
3
O
6
. The two strongest exchange couplings are
shown
have significant electronic coupling between the lay-
ers and therefore splitting in electronic bands [74].
The coupling between neighbouringbilayer blocksis
usually neglected when modelling the magnetic ex-
citations and the system treated as a two layer 2D sys-
tem. Because there is a mirror (symmetry) plane be-
tween the layers, eigenstates, including magnetic ex-
citations,will have either odd or even symmetry with
respect to the mirror plane leading to two distinct
types of magnetic excitation and therefore, for ex-
ample,two dispersion branches.YBa
2
Cu
3
O
6+x
is hole
doped by adding oxygen, the addition oxygen atoms
Fig. 18.15. Oxygen ordering phase diagram for
YBa
2
Cu
3
O
6+x
. Tetragonal phase (T) and various chain or-
dered phases (OI–OVIII) with different repeat distances
along the a-axis. (After Zimmermann et al. [76])
1008 S.M. Hayden
occupy sites between the Cu atoms outside the CuO
2
planes.For lightdopingthis occurs randomly andthe
structure remains tetragonal. For oxygen doping be-
yond x ≈ 0.3,the additional oxygen atoms order into
various chain structures (see Fig. 18.15). The ortho-
II (underdoped) and ortho-I structure (optimally
doped) structures are shown in Fig. 18.16. The chain
ordered compositions have orthorhombic symmetry
and crystals are typically highly twinned as grown.
Crystals may be de-twinned into a single orthorhom-
bic domain by annealing under uniaxial pressure.
In common with La
2−x
Sr
x
CuO
4
,YBa
2
Cu
3
O
6+x
also
shows spin freezing behaviour [75] which persists
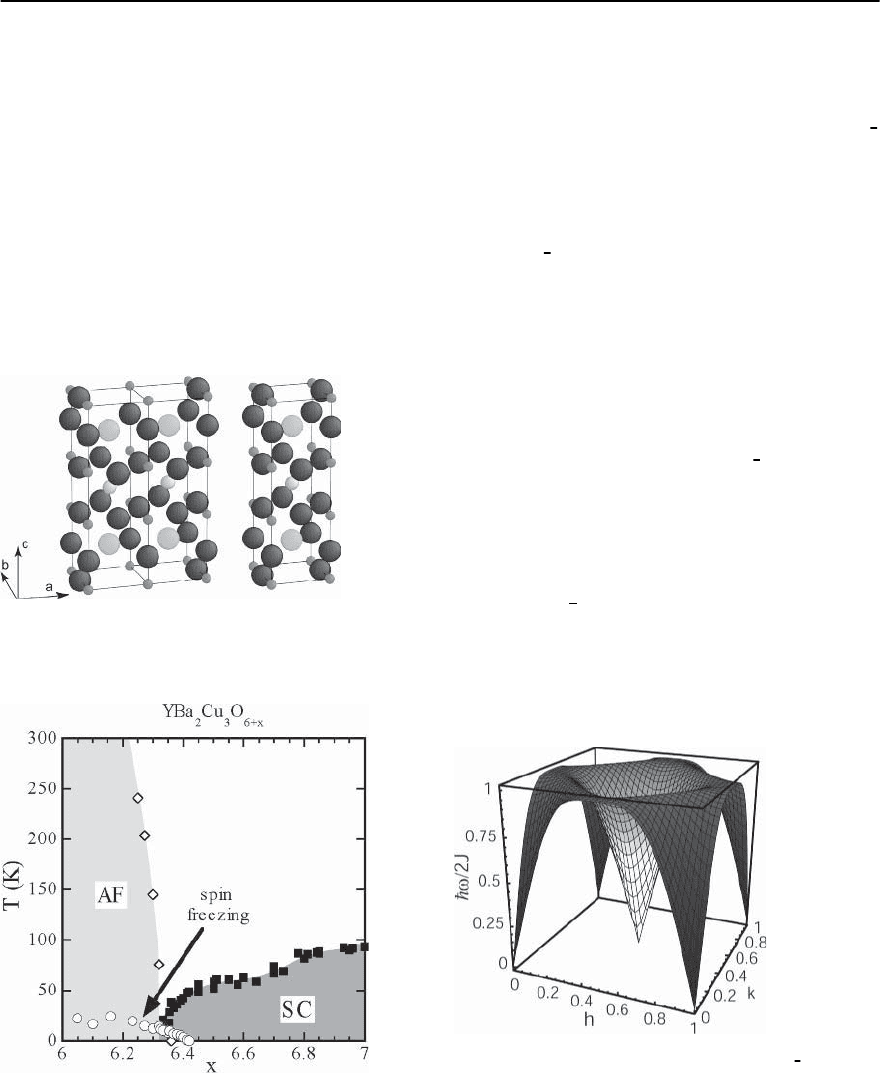
into the superconducting state (see Fig. 18.17).
Fig. 18.16. The ortho-II (left) and ortho-I(right)structures
of YBa
2
Cu
3
O
6+x
. As oxygen is added to YBa
2
Cu
3
O
6
,Cu-O
chains are formed
Fig. 18.17. The antiferromagnetic and superconducting
phases of YBa
2
Cu
3
O
6+x
. Data collected from [75,77–84]
18.6.2 Magnetic Excitations in the Parent Compounds
of the High-T
c
Superconductors
The crystal and electronic structure of La
2
CuO
4
make it a good physical realization of a 2D S =
1
2
Heisenberg antiferromagnet.We will start by review-
ing the nature of the magnetic excitations for such a
model system.
The 2D S =
1
2
Square Lattice Antiferromagnet
The properties of Heisenberg antiferromagnets
when quantum mechanics is taken into account have
been investigated for much of this century. It is well
known that in 1D, quantum fluctuations destabi-
lize the N´eel state completely. In higher dimensions,
quantum fluctuations lead to significant corrections
to the ground state energy [85,86] and spin-wave ex-
citations [87]. However, the 2D S =
1
2
square-lattice
antiferromagnet is thoughtto be ordered atzero tem-
perature. In practice, interplanar coupling leads to
ordering at finite temperatures in physical realiza-
tionssuchasLa
2
CuO
4
.The high anisotropy and large
exchange constant make La
2
CuO
4
a good realization
of a 2D S =
1
2
antiferromagnet, particularly when
we consider the excitations on a wide energy scale
comparable with 2J. As we shall see below, there are
deviations from ideal behaviour.
The magnetic scattering can be qualitatively sep-
arated into three contributions: (i) Bragg scattering;
Fig. 18.18. Spin wave dispersion for a 2D S =
1
2
antiferro-
magnet such as La
2
CuO
4
.Theshading shows the intensity
of the spin waves, lighter shading represents higher mag-
netic response
