Beer F.P., Johnston E.R., DeWolf J.T., Mazurek D.F. Mechanics of Materials
Подождите немного. Документ загружается.


Apago PDF Enhancer
107
SAMPLE PROBLEM 2.5
A circle of diameter d 5 9 in. is scribed on an unstressed aluminum plate
of thickness t 5
3
4
in. Forces acting in the plane of the plate later cause nor-
mal stresses s
x
5 12 ksi and s
z
5 20 ksi. For E 5 10 3 10
6
psi and n 5
1
3
,
determine the change in (a) the length of diameter AB, (b) the length of
diameter CD, (c) the thickness of the plate, (d) the volume of the plate.
SOLUTION
Hooke’s Law. We note that s
y
5 0. Using Eqs. (2.28) we find the
strain in each of the coordinate directions.
P
x
51
s
x
E
2
ns
y
E
2
ns
z
E
5
1
10 3 10
6
psi
c112 ksi22 0 2
1
3
120 ksi2d510.533 3 10
23
in./in.
P
y
52
ns
x
E
1
s
y
E
2
ns
z
E
5
1
10 3 10
6
psi
c2
1
3
112 ksi21 0 2
1
3
120 ksi2d521.067 3 10
23
in./in.
P
z
52
ns
x
E
2
ns
y
E
1
s
z
E
5
1
10 3 10
6
psi
c2
1
3
112 ksi22 0 1 120 ksi2d511.600 3 10
23
in./in.
a. Diameter AB. The change in length is d
ByA
5 P
x
d .
d
B
y
A
5 P
x
d 5 110.533 3 10
2
3
in./in.219 in.2
d
ByA
5 14.8 3 10
23
in.
◀
b. Diameter CD.
d
C
y
D
5 P
z
d 5 111.600 3 10
2
3
in./in.219 in.2
d
CyD
5 114.4 3 10
23
in.
◀
c. Thickness. Recalling that t 5
3
4
in., we have
d
t
5 P
y
t 5 121.067 3 10
23
in./in.21
3
4
in.2
d
t
5 20.800 3 10
23
in.
◀
d. Volume of the Plate. Using Eq. (2.30), we write
e 5 P
x
1 P
y
1 P
z
5 110.533 2 1.067 1 1.600210
2
3
511.067 3 10
2
3
¢V 5 eV 511.067 3 10
23
31
15 in.
21
15 in.
21
3
4
in.
24
¢V 510.187 3 in
3
◀
x
z
15 in.
15 in.
z
y
x
A
B
C
D
bee80288_ch02_052-139.indd Page 107 11/1/10 11:30:48 PM user-f499bee80288_ch02_052-139.indd Page 107 11/1/10 11:30:48 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02
Apago PDF Enhancer
PROBLEMS
108
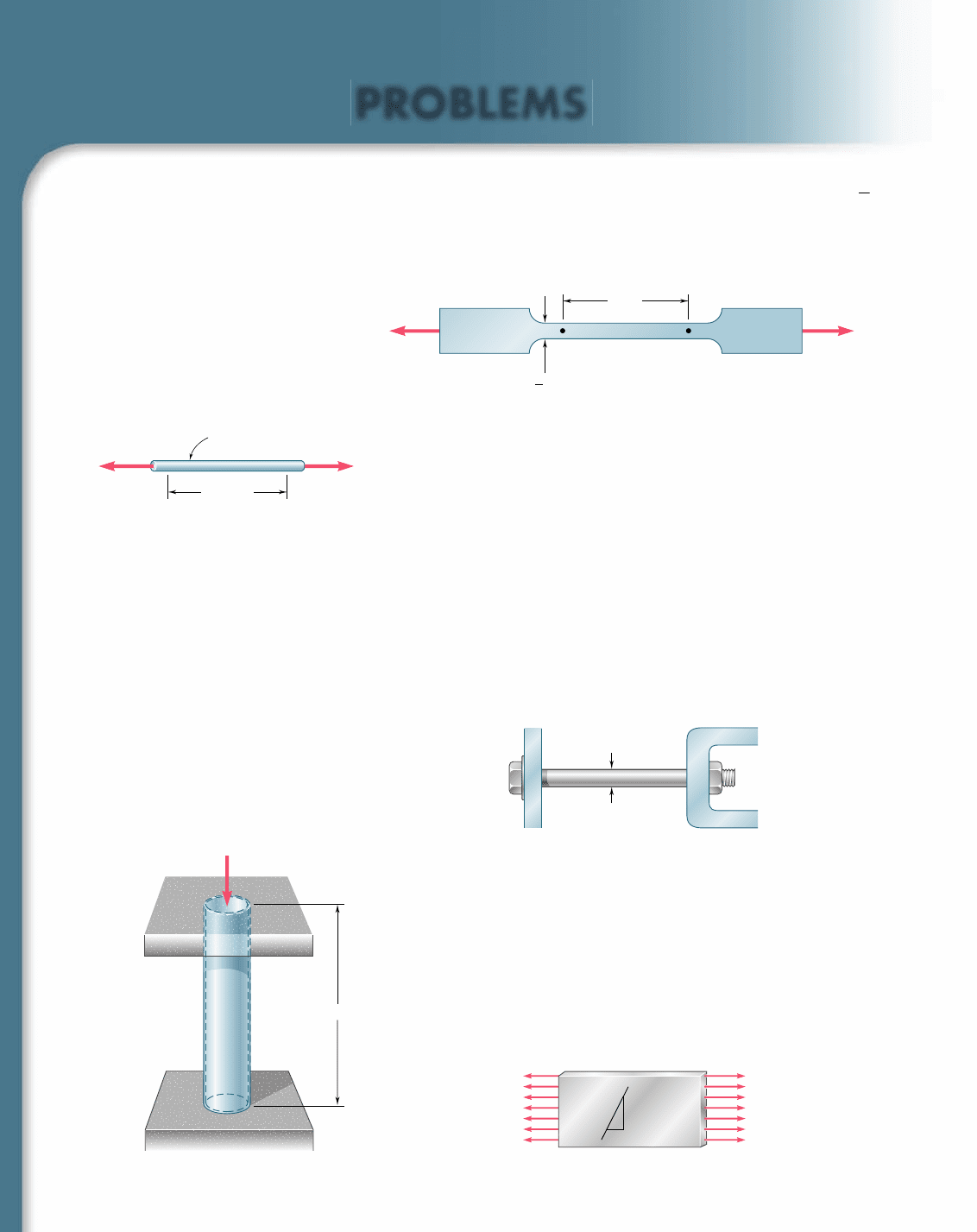
2.61 A 600-lb tensile load is applied to a test coupon made from
1
16
-in.
flat steel plate (E 5 29 3 10
6
psi, n 5 0.30). Determine the result-
ing change (a) in the 2-in. gage length, (b) in the width of portion
AB of the test coupon, (c) in the thickness of portion AB, (d) in
the cross-sectional area of portion AB.
600 lb
600 lb
2 in.
AB
in.
1
2
Fig. P2.61
2.62 In a standard tensile test a steel rod of 22-mm diameter is sub-
jected to a tension force of 75 kN. Knowing that n 5 0.3 and E 5
200 GPa, determine (a) the elongation of the rod in a 200-mm
gage length, (b) the change in diameter of the rod.
2.63 A 20-mm-diameter rod made of an experimental plastic is sub-
jected to a tensile force of magnitude P 5 6 kN. Knowing that an
elongation of 14 mm and a decrease in diameter of 0.85 mm are
observed in a 150-mm length, determine the modulus of elasticity,
the modulus of rigidity, and Poisson’s ratio for the material.
2.64 The change in diameter of a large steel bolt is carefully measured
as the nut is tightened. Knowing that E 5 29 3 10
6
psi and n 5
0.30, determine the internal force in the bolt, if the diameter is
observed to decrease by 0.5 3 10
23
in.
200 mm
22-mm diameter
75 kN 75 kN
Fig. P2.62
2.5 in.
Fig. P2.64
2.5 m
700 kN
Fig. P2.65
1
2
Fig. P2.66
2.65 A 2.5-m length of a steel pipe of 300-mm outer diameter and
15-mm wall thickness is used as a column to carry a 700-kN centric
axial load. Knowing that E 5 200 GPa and n 5 0.30, determine
(a) the change in length of the pipe, (b) the change in its outer
diameter, (c) the change in its wall thickness.
2.66 An aluminum plate (E 5 74 GPa, n 5 0.33) is subjected to a cen-
tric axial load that causes a normal stress s. Knowing that, before
loading, a line of slope 2:1 is scribed on the plate, determine the
slope of the line when s 5 125 MPa.
bee80288_ch02_052-139.indd Page 108 11/1/10 11:30:52 PM user-f499bee80288_ch02_052-139.indd Page 108 11/1/10 11:30:52 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02
Apago PDF Enhancer
109
Problems
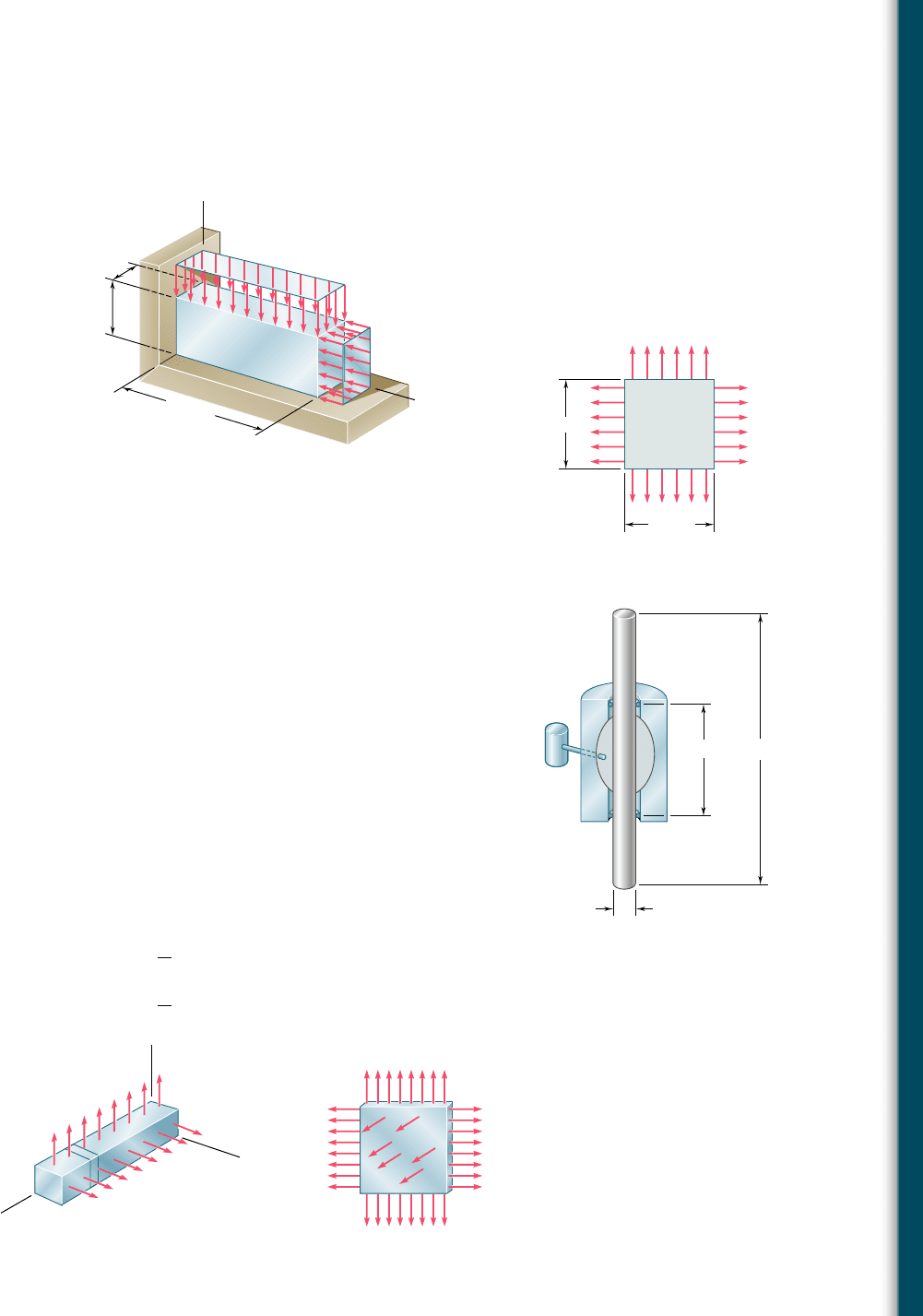
2.67 The block shown is made of a magnesium alloy for which E 5 45 GPa
and n 5 0.35. Knowing that s
x
5 2180 MPa, determine (a) the
magnitude of s
y
for which the change in the height of the block will
be zero, (b) the corresponding change in the area of the face ABCD,
(c) the corresponding change in the volume of the block.
40 mm
100 mm
x
z
y
x
y
C
B
D
G
F
A
E
25 mm
Fig. P2.67
2.68 A 30-mm square was scribed on the side of a large steel pressure
vessel. After pressurization the biaxial stress condition at the square
is as shown. For E 5 200 GPa and n 5 0.30, determine the change
in length of (a) side AB, (b) side BC, (c) diagonal AC.
2.69 The aluminum rod AD is fitted with a jacket that is used to apply
a hydrostatic pressure of 6000 psi to the 12-in. portion BC of the
rod. Knowing that E 5 10.1 3 10
6
psi and n 5 0.36, determine
(a) the change in the total length AD, (b) the change in diameter
at the middle of the rod.
2.70 For the rod of Prob. 2.69, determine the forces that should be applied
to the ends A and D of the rod (a) if the axial strain in portion BC
of the rod is to remain zero as the hydrostatic pressure is applied,
(b) if the total length AD of the rod is to remain unchanged.
2.71 In many situations physical constraints prevent strain from occurring
in a given direction. For example, P
z
5 0 in the case shown, where
longitudinal movement of the long prism is prevented at every point.
Plane sections perpendicular to the longitudinal axis remain plane
and the same distance apart. Show that for this situation, which is
known as plane strain, we can express s
z
, P
x
, and P
y
as follows:
s
z
5 n1s
x
1 s
y
2
P
x
5
1
E
311 2 n
2
2s
x
2 n11 1 n2s
y
4
P
y
5
1
E
311 2 n
2
2s
y
2 n11 1 n2s
x
4
y
40 MPa
x
80 MP
a
30 mm
A
B
C
D
30 mm
Fig. P2.68
12 in.
20 in.
C
D
A
B
1.5 in.
Fig. P2.69
xx
zz
yy
y
x
z
(a)(b)
Fig. P2.71
bee80288_ch02_052-139.indd Page 109 11/1/10 11:31:14 PM user-f499bee80288_ch02_052-139.indd Page 109 11/1/10 11:31:14 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02
Apago PDF Enhancer
110
Stress and Strain—Axial Loading
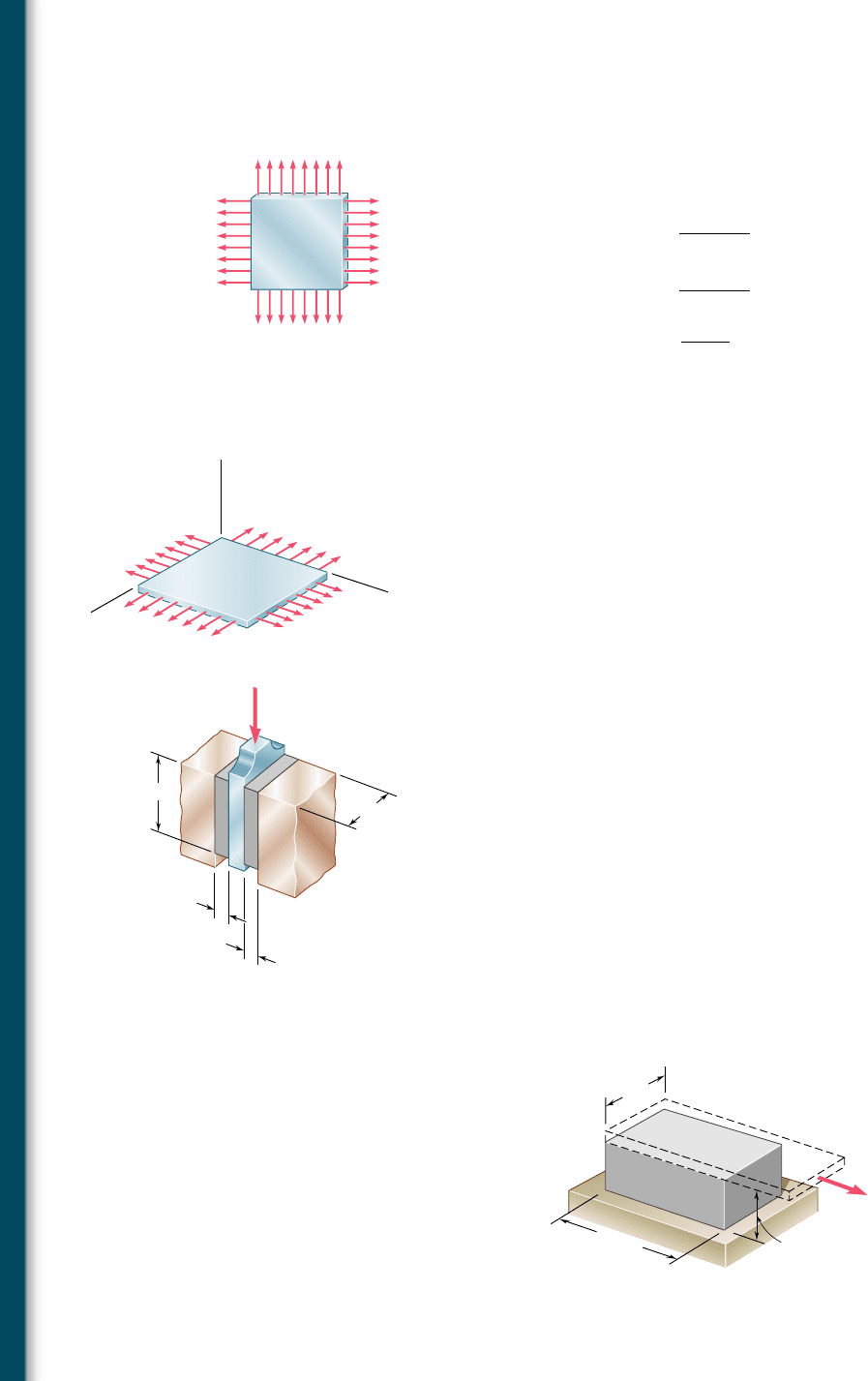
2.72 In many situations it is known that the normal stress in a given
direction is zero. For example, s
z
5 0 in the case of the thin plate
shown. For this case, which is known as plane stress, show that if
the strains P
x
and P
y
have been determined experimentally, we can
express s
x
, s
y
and P
z
as follows:
s
x
5 E
P
x
1 nP
y
1
2
n
2
s
y
5 E
P
y
1 nP
x
1
2
n
2
P
z
52
n
1
2
n
1P
x
1 P
y
2
2.73 For a member under axial loading, express the normal strain P9 in
a direction forming an angle of 458 with the axis of the load in
terms of the axial strain P
x
by (a) comparing the hypotenuses of
the triangles shown in Fig. 2.50, which represent respectively an
element before and after deformation, (b) using the values of the
corresponding stresses s9 and s
x
shown in Fig. 1.38, and the gen-
eralized Hooke’s law.
2.74 The homogeneous plate ABCD is subjected to a biaxial loading as
shown. It is known that s
z
5 s
0
and that the change in length of
the plate in the x direction must be zero, that is, P
x
5 0. Denoting
by E the modulus of elasticity and by n Poisson’s ratio, determine
(a) the required magnitude of s
x
, (b) the ratio s
0
yP
z
.
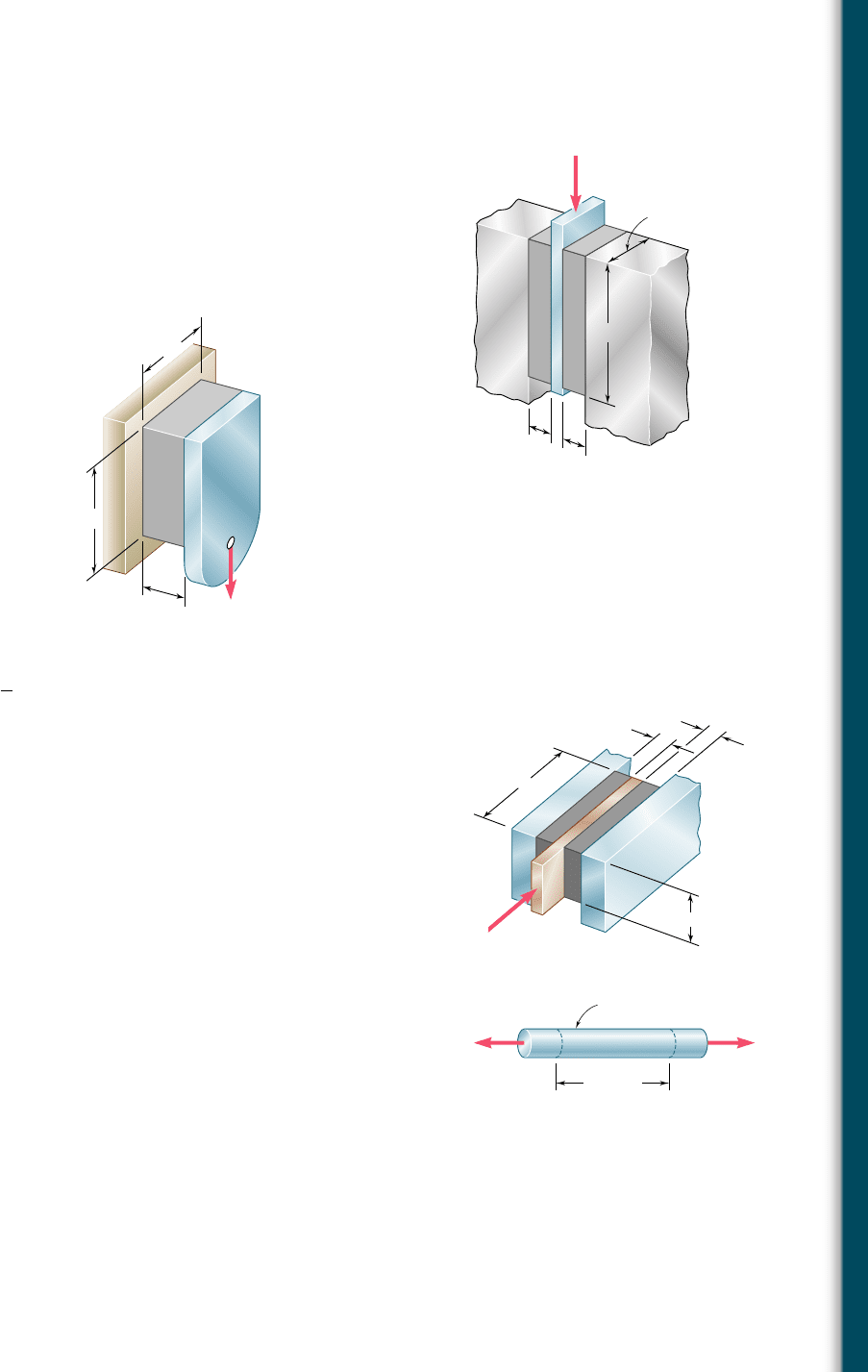
2.75 A vibration isolation unit consists of two blocks of hard rubber
bonded to a plate AB and to rigid supports as shown. Knowing that
a force of magnitude P 5 25 kN causes a deflection d 5 1.5 mm
of plate AB, determine the modulus of rigidity of the rubber
used.
2.76 A vibration isolation unit consists of two blocks of hard rubber with
a modulus of rigidity G 5 19 MPa bonded to a plate AB and to
rigid supports as shown. Denoting by P the magnitude of the force
applied to the plate and by d the corresponding deflection, deter-
mine the effective spring constant, k 5 Pyd, of the system.
2.77 The plastic block shown is bonded to a fixed base and to a hori-
zontal rigid plate to which a force P is applied. Knowing that for
the plastic used G 5 55 ksi, determine the deflection of the plate
when P 5 9 kips.
x
y
Fig. P2.72
x
z
z
y
x
A
B
C
D
Fig. P2.74
3.5 in.
5.5 in.
2.2 in.
P
Fig. P2.77
150 mm
100 mm
30 mm
B
A
30 mm
P
Fig. P2.75 and P2.76
bee80288_ch02_052-139.indd Page 110 9/4/10 5:19:15 PM user-f499bee80288_ch02_052-139.indd Page 110 9/4/10 5:19:15 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02
Apago PDF Enhancer
111
Problems
2.78 A vibration isolation unit consists of two blocks of hard rubber
bonded to plate AB and to rigid supports as shown. For the type
and grade of rubber used t
all
5 220 psi and G 5 1800 psi. Know-
ing that a centric vertical force of magnitude P 5 3.2 kips must
cause a 0.1-in. vertical deflection of the plate AB, determine the
smallest allowable dimensions a and b of the block.
2.79 The plastic block shown is bonded to a rigid support and to a verti-
cal plate to which a 55-kip load P is applied. Knowing that for the
plastic used G 5 150 ksi, determine the deflection of the plate.
2.80 What load P should be applied to the plate of Prob. 2.79 to pro-
duce a
1
16
-in. deflection?
2.81 Two blocks of rubber with a modulus of rigidity G 5 12 MPa are
bonded to rigid supports and to a plate AB. Knowing that c 5 100 mm
and P 5 45 kN, determine the smallest allowable dimensions a and
b of the blocks if the shearing stress in the rubber is not to exceed
1.4 MPa and the deflection of the plate is to be at least 5 mm.
2.82 Two blocks of rubber with a modulus of rigidity G 5 10 MPa are
bonded to rigid supports and to a plate AB. Knowing that b 5
200 mm and c 5 125 mm, determine the largest allowable load P
and the smallest allowable thickness a of the blocks if the shearing
stress in the rubber is not to exceed 1.5 MPa and the deflection
of the plate is to be at least 6 mm.
*2.83 Determine the dilatation e and the change in volume of the
200-mm length of the rod shown if (a) the rod is made of steel
with E 5 200 GPa and n 5 0.30, (b) the rod is made of aluminum
with E 5 70 GPa and n 5 0.35.
*2.84 Determine the change in volume of the 2-in. gage length segment
AB in Prob. 2.61 (a) by computing the dilatation of the material,
(b) by subtracting the original volume of portion AB from its final
volume.
*2.85 A 6-in.-diameter solid steel sphere is lowered into the ocean to a
point where the pressure is 7.1 ksi (about 3 miles below the surface).
Knowing that E 5 29 3 10
6
psi and n 5 0.30, determine (a) the
decrease in diameter of the sphere, (b) the decrease in volume of
the sphere, (c) the percent increase in the density of the sphere.
B
b
A
3.0 in.
P
a
a
Fig. P2.78
4.8 in.
3.2 in.
2 in.
P
Fig. P2.79
a
a
c
b
A
B
P
Figs. P2.81 and P2.82
46 kN46 kN
200 mm
22-mm diameter
Fig. P2.83
bee80288_ch02_052-139.indd Page 111 9/4/10 5:19:23 PM user-f499bee80288_ch02_052-139.indd Page 111 9/4/10 5:19:23 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02
Apago PDF Enhancer
112
Stress and Strain—Axial Loading
*2.86 (a) For the axial loading shown, determine the change in height
and the change in volume of the brass cylinder shown. (b) Solve
part a, assuming that the loading is hydrostatic with s
x
5 s
y
5
s
z
5 270 MPa.
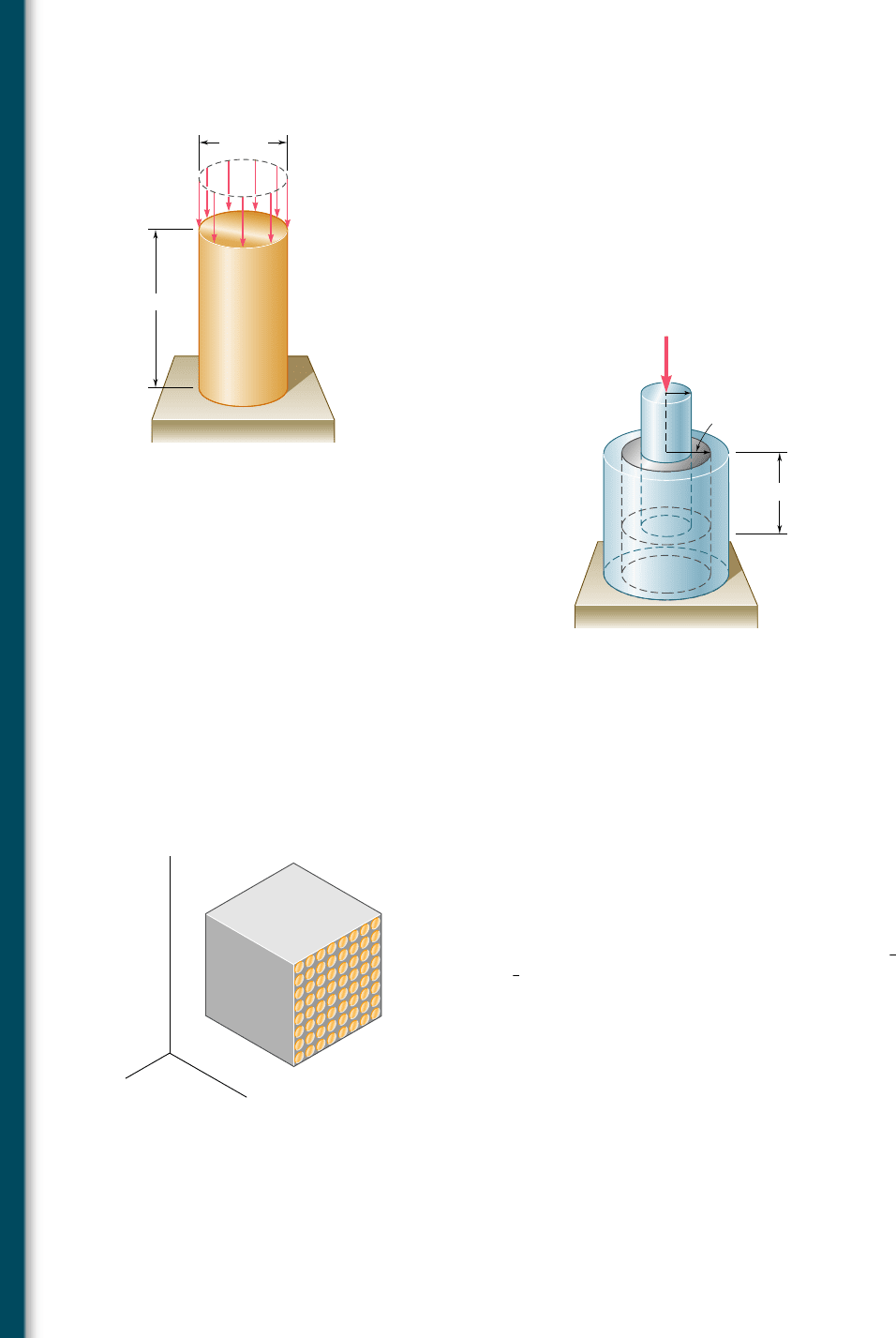
*2.87 A vibration isolation support consists of a rod A of radius R
1
5
10 mm and a tube B of inner radius R
2
5 25 mm bonded to an
80-mm-long hollow rubber cylinder with a modulus of rigidity
G 5 12 MPa. Determine the largest allowable force P that can be
applied to rod A if its deflection is not to exceed 2.50 mm.
E
105 GPa
y
58 MP
a
v 0.33
135 mm
85 mm
Fig. P2.86
A
B
R
1
80 mm
R
2
P
Fig. P2.87 and P2.88
*2.88 A vibration isolation support consists of a rod A of radius R
1
and
a tube B of inner radius R
2
bonded to an 80-mm-long hollow rub-
ber cylinder with a modulus of rigidity G 5 10.93 MPa. Determine
the required value of the ratio R
2
yR
1
if a 10-kN force P is to cause
a 2-mm deflection of rod A.
*2.89 The material constants E, G, k, and n are related by Eqs. (2.33)
and (2.43). Show that any one of the constants may be expressed
in terms of any other two constants. For example, show that (a) k 5
GEy(9G 2 3E) and (b) n 5 (3k 2 2G)y(6k 1 2G).
*2.90 Show that for any given material, the ratio G/E of the modulus of
rigidity over the modulus of elasticity is always less than
1
2
but more
than
1
3
. [Hint: Refer to Eq. (2.43) and to Sec. 2.13.]
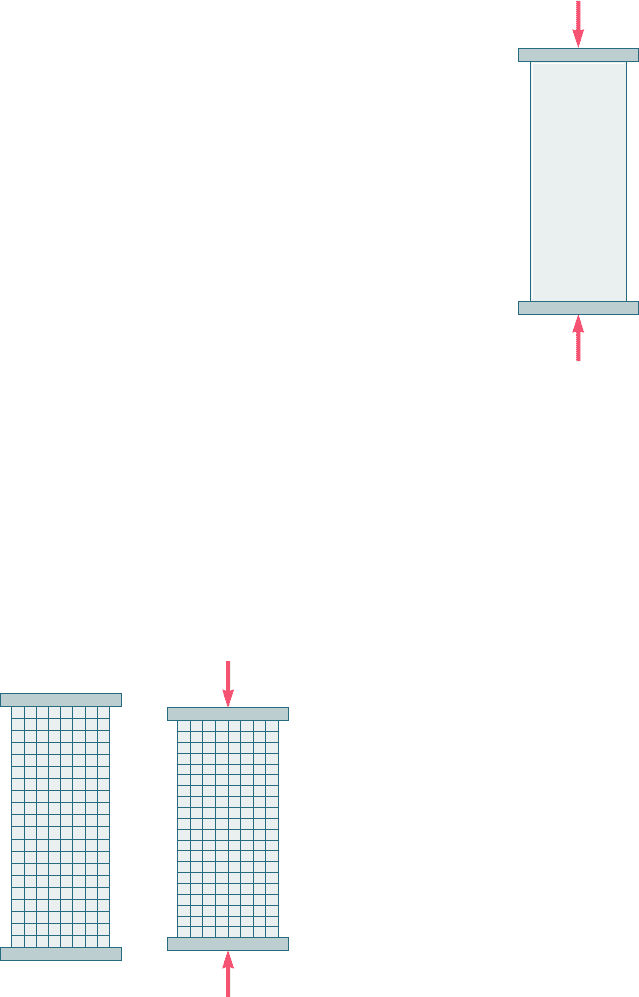
*2.91 A composite cube with 40-mm sides and the properties shown is
made with glass polymer fibers aligned in the x direction. The cube
is constrained against deformations in the y and z directions and
is subjected to a tensile load of 65 kN in the x direction. Determine
(a) the change in the length of the cube in the x direction, (b) the
stresses s
x
, s
y
, and s
z
.
*2.92 The composite cube of Prob. 2.91 is constrained against defor-
mation in the z direction and elongated in the x direction by
0.035 mm due to a tensile load in the x direction. Determine
(a) the stresses s
x
, s
y
, and s
z
, (b) the change in the dimension
in the y direction.
E
x
50 GPa
E
y
15.2 GPa
E
z
15.2 GPa
xz
0.254
xy
0.254
zy
0.428
y
z
x
Fig. P2.91
bee80288_ch02_052-139.indd Page 112 9/4/10 5:19:31 PM user-f499bee80288_ch02_052-139.indd Page 112 9/4/10 5:19:31 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02
Apago PDF Enhancer
113
2.17 STRESS AND STRAIN DISTRIBUTION UNDER
AXIAL LOADING; SAINT-VENANT’S PRINCIPLE
We have assumed so far that, in an axially loaded member, the nor-
mal stresses are uniformly distributed in any section perpendicular
to the axis of the member. As we saw in Sec. 1.5, such an assumption
may be quite in error in the immediate vicinity of the points of
application of the loads. However, the determination of the actual
stresses in a given section of the member requires the solution of a
statically indeterminate problem.
In Sec. 2.9, you saw that statically indeterminate problems
involving the determination of forces can be solved by considering
the deformations caused by these forces. It is thus reasonable to
conclude that the determination of the stresses in a member requires
the analysis of the strains produced by the stresses in the member.
This is essentially the approach found in advanced textbooks, where
the mathematical theory of elasticity is used to determine the distri-
bution of stresses corresponding to various modes of application of
the loads at the ends of the member. Given the more limited math-
ematical means at our disposal, our analysis of stresses will be
restricted to the particular case when two rigid plates are used to
transmit the loads to a member made of a homogeneous isotropic
material (Fig. 2.54).
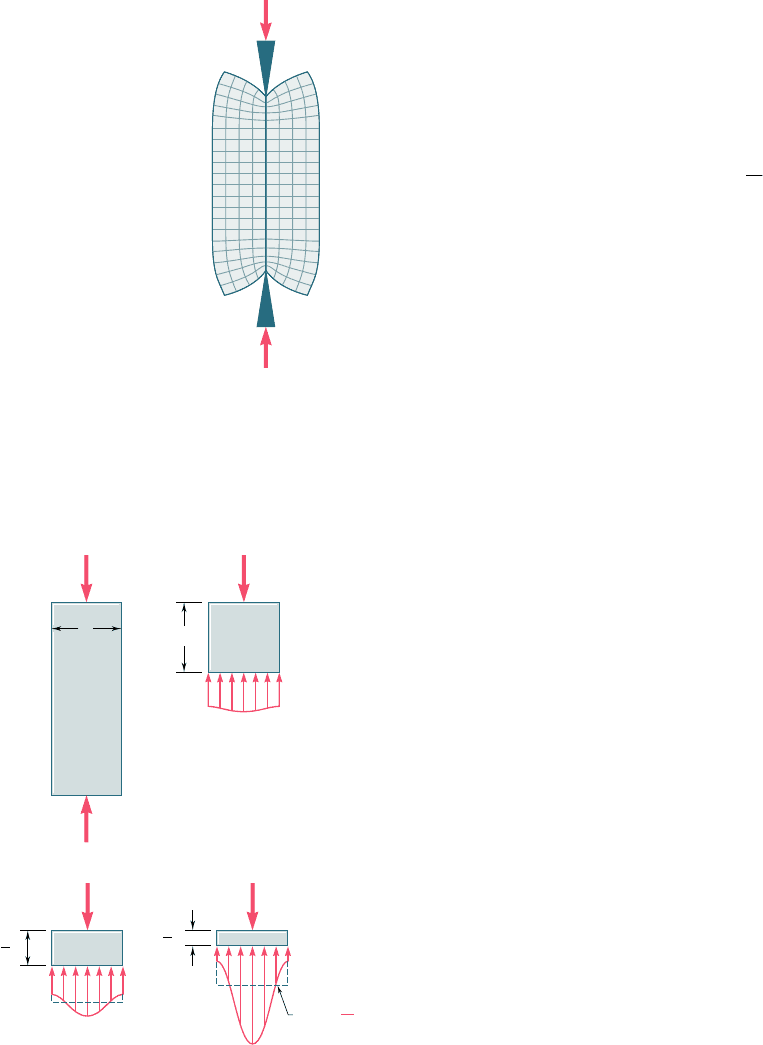
If the loads are applied at the center of each plate,† the plates
will move toward each other without rotating, causing the member
to get shorter, while increasing in width and thickness. It is reason-
able to assume that the member will remain straight, that plane
sections will remain plane, and that all elements of the member will
deform in the same way, since such an assumption is clearly compat-
ible with the given end conditions. This is illustrated in Fig. 2.55,
2.17 Stress and Strain Distribution under Axial
Loading; Saint-Venant’s Principle
P
P'
Fig. 2.54 Axial load applied
by rigid plates to a member.
†More precisely, the common line of action of the loads should pass through the centroid
of the cross section (cf. Sec. 1.5).
(a)(b)
P
P'
Fig. 2.55 Axial load applied by rigid
plates to rubber model.
bee80288_ch02_052-139.indd Page 113 9/7/10 4:34:35 PM user-f499bee80288_ch02_052-139.indd Page 113 9/7/10 4:34:35 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch07/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch07
Apago PDF Enhancer
114
Stress and Strain—Axial Loading
which shows a rubber model before and after loading.† Now, if all
elements deform in the same way, the distribution of strains through-
out the member must be uniform. In other words, the axial strain P
y
and the lateral strain P
x
5 2nP
y
are constant. But, if the stresses do
not exceed the proportional limit, Hooke’s law applies and we may
write s
y
5 EP
y
, from which it follows that the normal stress s
y
is
also constant. Thus, the distribution of stresses is uniform throughout
the member and, at any point,
s
y
5 1s
y
2
ave
5
P
A
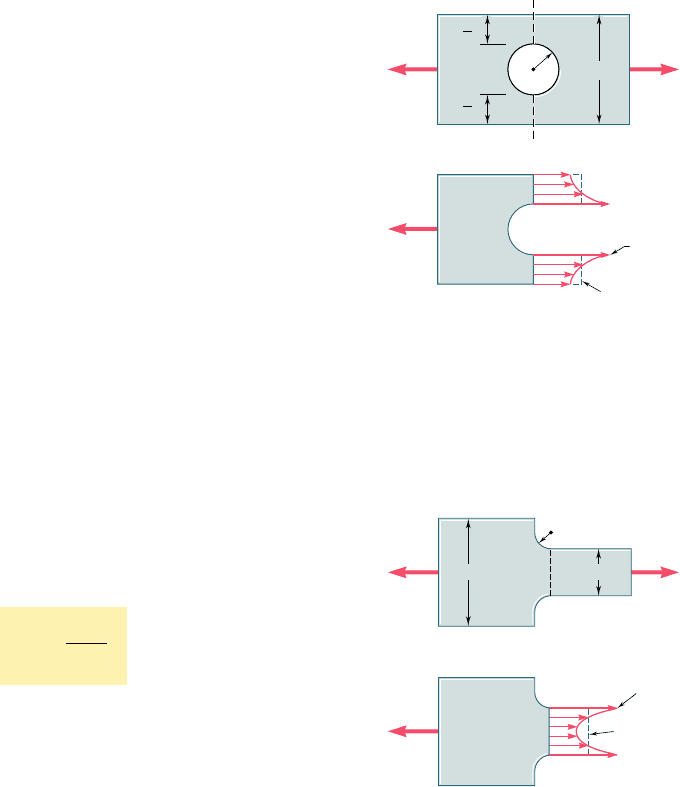
On the other hand, if the loads are concentrated, as illustrated
in Fig. 2.56, the elements in the immediate vicinity of the points of
application of the loads are subjected to very large stresses, while
other elements near the ends of the member are unaffected by the
loading. This may be verified by observing that strong deformations,
and thus large strains and large stresses, occur near the points of
application of the loads, while no deformation takes place at the
corners. As we consider elements farther and farther from the ends,
however, we note a progressive equalization of the deformations
involved, and thus a more nearly uniform distribution of the strains
and stresses across a section of the member. This is further illustrated
in Fig. 2.57, which shows the result of the calculation by advanced
mathematical methods of the distribution of stresses across various
sections of a thin rectangular plate subjected to concentrated loads.
We note that at a distance b from either end, where b is the width
of the plate, the stress distribution is nearly uniform across the sec-
tion, and the value of the stress s
y
at any point of that section can
be assumed equal to the average value PyA. Thus, at a distance equal
to, or greater than, the width of the member, the distribution of
stresses across a given section is the same, whether the member is
loaded as shown in Fig. 2.54 or Fig. 2.56. In other words, except in
the immediate vicinity of the points of application of the loads, the
stress distribution may be assumed independent of the actual mode
of application of the loads. This statement, which applies not only to
axial loadings, but to practically any type of load, is known as Saint-
Venant’s principle, after the French mathematician and engineer
Adhémar Barré de Saint-Venant (1797–1886).
While Saint-Venant’s principle makes it possible to replace a
given loading by a simpler one for the purpose of computing the
stresses in a structural member, you should keep in mind two impor-
tant points when applying this principle:
1. The actual loading and the loading used to compute the stresses
must be statically equivalent.
2. Stresses cannot be computed in this manner in the immediate
vicinity of the points of application of the loads. Advanced theo-
retical or experimental methods must be used to determine the
distribution of stresses in these areas.
P
P'
Fig. 2.56 Concentrated
axial load applied to
rubber model.
†Note that for long, slender members, another configuration is possible, and indeed will
prevail, if the load is sufficiently large; the member buckles and assumes a curved shape.
This will be discussed in Chap. 10.
b
b
min
ave
0.973
max
ave
1.027
PP
P'
b
1
2
b
1
4
min
ave
max
P
A
min
ave
0.668
max
ave
1.387
min
ave
0.198
max
ave
2.575
PP
Fig. 2.57 Stress distributions in a plate under
concentrated axial loads.
bee80288_ch02_052-139.indd Page 114 9/7/10 4:34:35 PM user-f499bee80288_ch02_052-139.indd Page 114 9/7/10 4:34:35 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch07/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch07
Apago PDF Enhancer
115
You should also observe that the plates used to obtain a uniform
stress distribution in the member of Fig. 2.55 must allow the mem-
ber to freely expand laterally. Thus, the plates cannot be rigidly
attached to the member; you must assume them to be just in contact
with the member, and smooth enough not to impede the lateral
expansion of the member. While such end conditions can actually be
achieved for a member in compression, they cannot be physically
realized in the case of a member in tension. It does not matter,
however, whether or not an actual fixture can be realized and used
to load a member so that the distribution of stresses in the member
is uniform. The important thing is to imagine a model that will allow
such a distribution of stresses, and to keep this model in mind so
that you may later compare it with the actual loading conditions.
2.18 STRESS CONCENTRATIONS
As you saw in the preceding section, the stresses near the points of
application of concentrated loads can reach values much larger than
the average value of the stress in the member. When a structural
member contains a discontinuity, such as a hole or a sudden change
in cross section, high localized stresses can also occur near the dis-
continuity. Figures 2.58 and 2.59 show the distribution of stresses in
critical sections corresponding to two such situations. Figure 2.58
refers to a flat bar with a circular hole and shows the stress distribu-
tion in a section passing through the center of the hole. Figure 2.59
refers to a flat bar consisting of two portions of different widths con-
nected by fillets; it shows the stress distribution in the narrowest part
of the connection, where the highest stresses occur.
These results were obtained experimentally through the use of
a photoelastic method. Fortunately for the engineer who has to
design a given member and cannot afford to carry out such an analy-
sis, the results obtained are independent of the size of the member
and of the material used; they depend only upon the ratios of the
geometric parameters involved, i.e., upon the ratio ryd in the case
of a circular hole, and upon the ratios ryd and Dyd in the case of
fillets. Furthermore, the designer is more interested in the maximum
value of the stress in a given section, than in the actual distribution
of stresses in that section, since the main concern is to determine
whether the allowable stress will be exceeded under a given loading,
and not where this value will be exceeded. For this reason, one
defines the ratio
K 5
s
max
s
ave
(2.48)
of the maximum stress over the average stress computed in the
critical (narrowest) section of the discontinuity. This ratio is referred
to as the stress-concentration factor of the given discontinuity. Stress-
concentration factors can be computed once and for all in terms of
the ratios of the geometric parameters involved, and the results
obtained can be expressed in the form of tables or of graphs, as
2.18 Stress Concentrations
PP'
P'
r
D
d
1
2
d
1
2
max
ave
Fig. 2.58 Stress distribution near circular
hole in flat bar under axial loading.
PP'
P'
max
ave
dD
r
Fig. 2.59 Stress distribution near fillets
in flat bar under axial loading.
bee80288_ch02_052-139.indd Page 115 9/4/10 5:19:47 PM user-f499bee80288_ch02_052-139.indd Page 115 9/4/10 5:19:47 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02
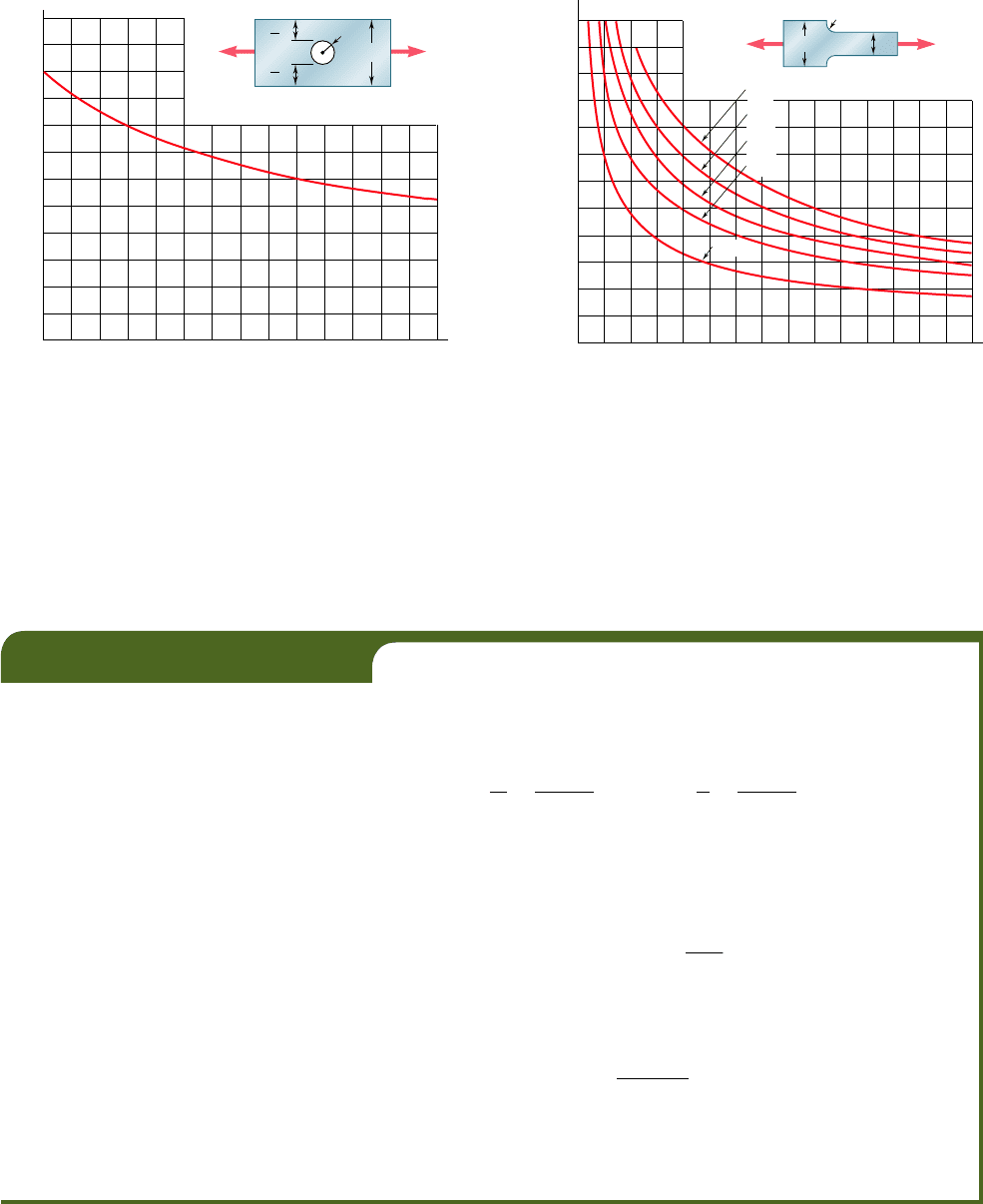
Apago PDF Enhancer
P' P
3.0
3.2
3.4
2.8
2.6
2.4
2.2
2.0
K
1.8
1.6
1.4
1.2
1.0
0 0.02 0.04 0.06 0.08 0.10 0.12 0.14 0.180.16 0.20 0.22 0.24 0.26 0.28 0.30
d
r
D
D/d 2
1.5
1.3
1.2
1.1
r/d
P' P
3.0
3.2
3.4
2.8
2.6
2.4
2.2
2.0
K
1.8
1.6
1.4
1.2
1.0
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7
2r/D
1
2
d
D
1
2
d
r
Fig. 2.60 Stress concentration factors for flat
bars under axial loading
†
Note that the average stress must be computed
across the narrowest section: s
ave
5 P/td, where
t is the thickness of the bar.
(a) Flat bars with holes (b) Flat bars with fillets
Determine the largest axial load P that can be safely supported by a flat
steel bar consisting of two portions, both 10 mm thick and, respectively,
40 and 60 mm wide, connected by fillets of radius r 5 8 mm. Assume an
allowable normal stress of 165 MPa.
We first compute the ratios
D
d
5
60 mm
40
mm
5 1.50
r
d
5
8 mm
40
mm
5 0.20
Using the curve in Fig. 2.60b corresponding to Dyd 5 1.50, we find that
the value of the stress-concentration factor corresponding to ryd 5 0.20 is
K 5 1.82
Carrying this value into Eq. (2.48) and solving for s
ave
, we have
s
ave
5
s
max
1.8
2
But s
max
cannot exceed the allowable stress s
all
5 165 MPa. Substituting
this value for s
max
, we find that the average stress in the narrower portion
(d 5 40 mm) of the bar should not exceed the value
s
ave
5
165 MPa
1
.
82
5 90.7 MPa
Recalling that s
ave
5 PyA, we have
P 5 As
ave
5
1
40 mm
21
10 mm
21
90.7 MPa
2
5 36.3 3 10
3
N
P 5 36
.
3
k
N
EXAMPLE 2.12
†W. D. Pilkey, Peterson’s Stress Concentration Factors, 2
nd
ed., John Wiley & Sons, New
York, 1997.
shown in Fig. 2.60. To determine the maximum stress occurring near a
discontinuity in a given member subjected to a given axial load P, the
designer needs only to compute the average stress s
ave
5 PyA in the
critical section, and multiply the result obtained by the appropriate value
of the stress-concentration factor K. You should note, however, that this
procedure is valid only as long as s
max
does not exceed the proportional
limit of the material, since the values of K plotted in Fig. 2.60 were
obtained by assuming a linear relation between stress and strain.
116
bee80288_ch02_052-139.indd Page 116 11/1/10 11:31:28 PM user-f499bee80288_ch02_052-139.indd Page 116 11/1/10 11:31:28 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02
