Beer F.P., Johnston E.R., DeWolf J.T., Mazurek D.F. Mechanics of Materials

Подождите немного. Документ загружается.

Apago PDF Enhancer

SAMPLE PROBLEM 2.4

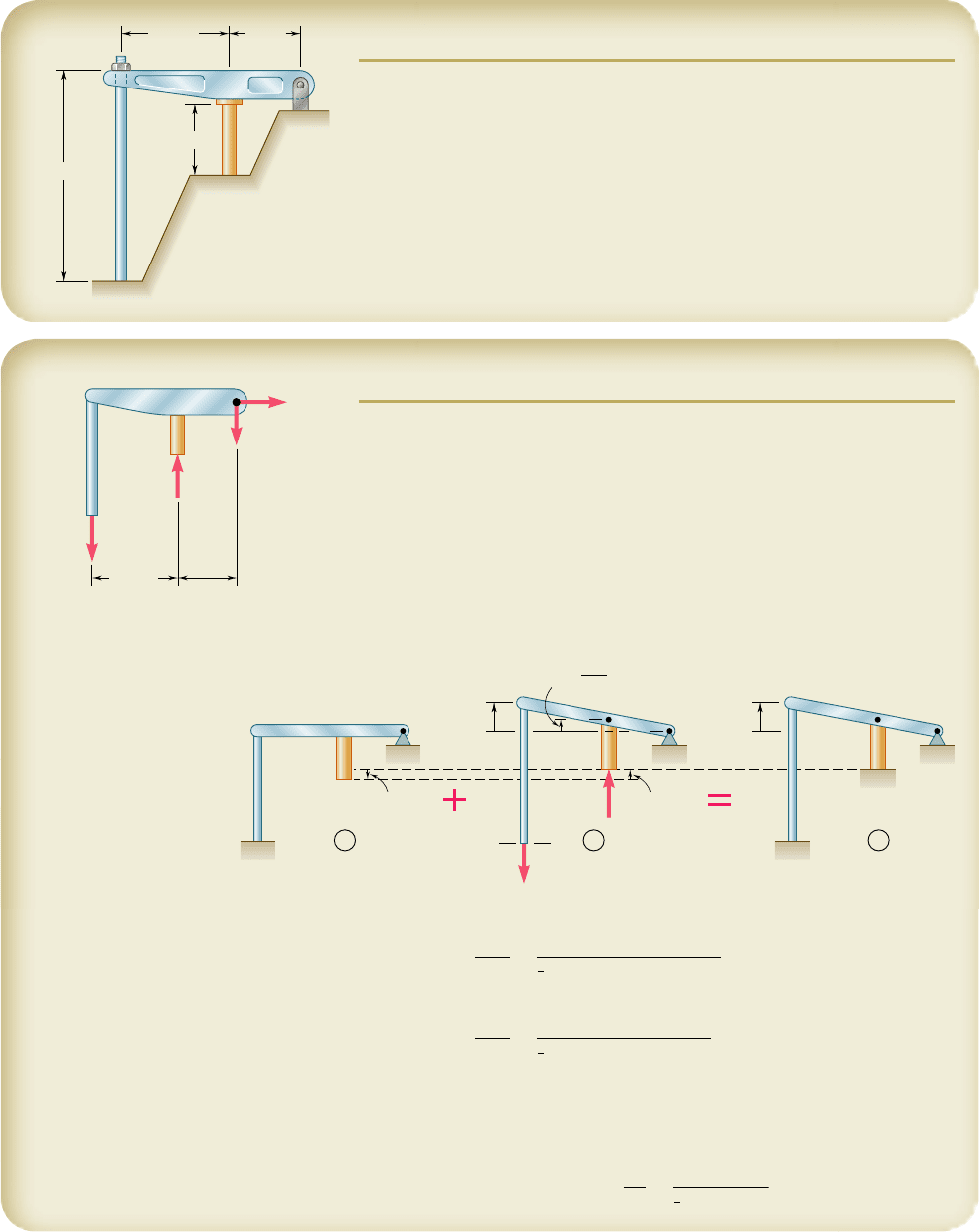
The rigid bar CDE is attached to a pin support at E and rests on the 30-mm-

diameter brass cylinder BD. A 22-mm-diameter steel rod AC passes through

a hole in the bar and is secured by a nut which is snugly fitted when the

temperature of the entire assembly is 208C. The temperature of the brass

cylinder is then raised to 508C while the steel rod remains at 208C. Assum-

ing that no stresses were present before the temperature change, determine

the stress in the cylinder.

Rod AC: Steel Cylinder BD: Brass

E 5 200 GPa E 5 105 GPa

a 5 11.7 3 10

/°C a 5 20.9 3 10

/°C

SOLUTION

Statics. Considering the free body of the entire assembly, we write

o M

5 0: R

0.75 m

2 R

0.3 m

5 0R

5 0.4R

(1)

Deformations. We use the method of superposition, considering R

redundant. With the support at B removed, the temperature rise of the cylinder

causes point B to move down through d

. The reaction R

must cause a deflec-

tion d

equal to d

so that the final deflection of B will be zero (Fig. 3).

Deflection d

. Because of a temperature rise of 508 2 208 5 308C,

the length of the brass cylinder increases by d

5 L

¢T

a 5

0.3 m



30°C



20.9 3 10

/°C

5 188.1 3 10

m w

0.9 m

0.3 m

0.45 m 0.3 m

1 2



0.3

0.4

0.75







Deflection d

. We note that d

5 0.4d

and d

5 d

1 d

ByD

0.9 m

0.022 m

200 GPa

5 11.84 3 10

5 0.40d

5 0.4

11.84 3 10

5 4.74 3 10

0.3 m

0.03 m

105 GPa

5 4.04 3 10

We recall from (1) that R

5 0.4R

and write

5 d

1 d

5 34.7410.4R

21 4.04R

410

5 5.94 3 10

But d

5 d

: 188.1 3 10

m 5 5.94 3 10

5 31.7 kN

Stress in Cylinder:

31.7

0.03 m

MPa

◀

0.3 m

0.45 m

bee80288_ch02_052-139.indd Page 87 11/1/10 11:30:09 PM user-f499bee80288_ch02_052-139.indd Page 87 11/1/10 11:30:09 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02

Apago PDF Enhancer

PROBLEMS

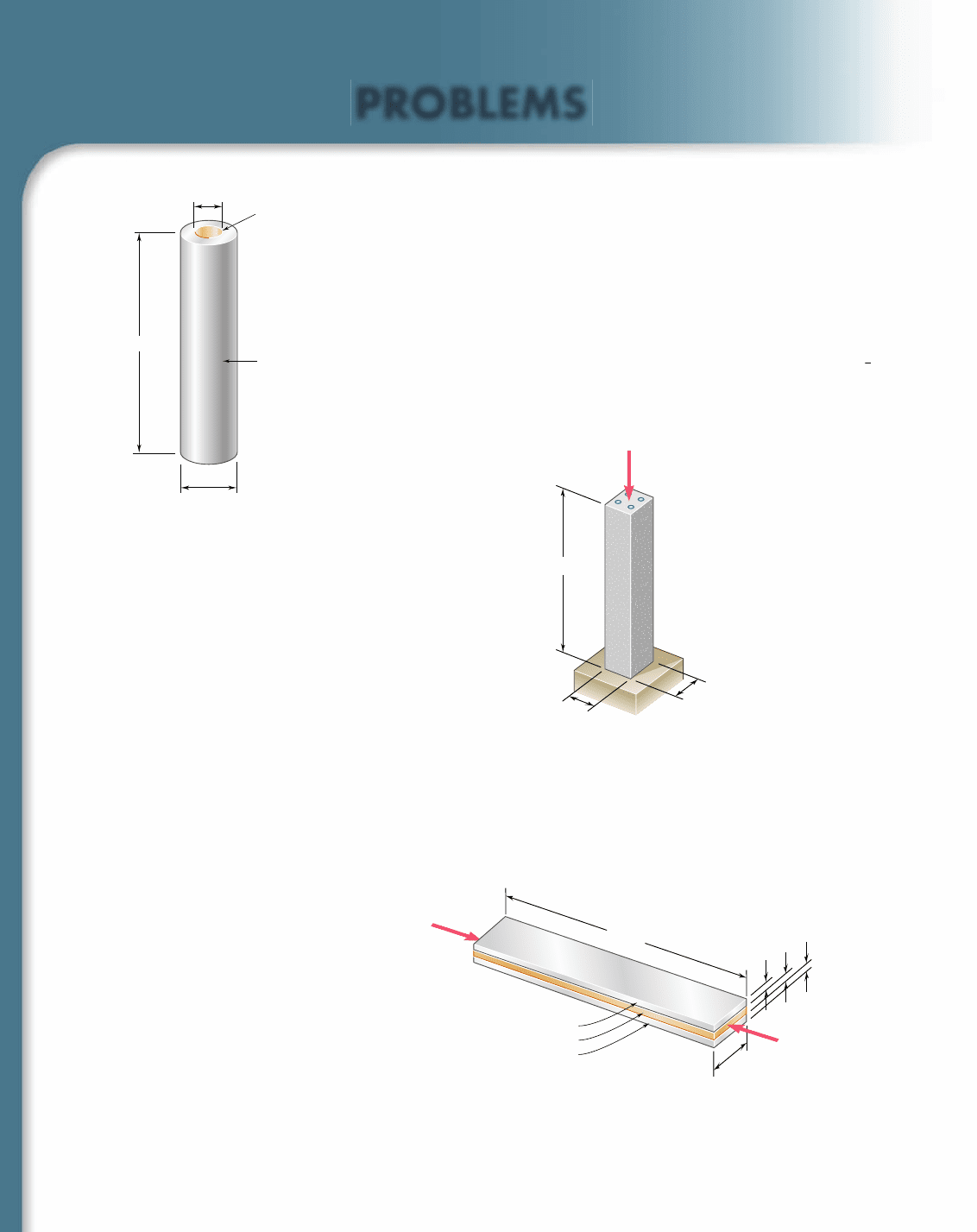
2.33 An axial force of 200 kN is applied to the assembly shown by means

of rigid end plates. Determine (a) the normal stress in the alumi-

num shell, (b) the corresponding deformation of the assembly.

2.34 The length of the assembly shown decreases by 0.40 mm when an

axial force is applied by means of rigid end plates. Determine

(a) the magnitude of the applied force, (b) the corresponding stress

in the brass core.

2.35 A 4-ft concrete post is reinforced with four steel bars, each with a

-in.

diameter. Knowing that E

5 29 3 10

psi and E

5 3.6 3 10

psi,

determine the normal stresses in the steel and in the concrete when

a 150-kip axial centric force P is applied to the post.

300 mm

60 mm

Aluminium shell

E  70 GPa

Brass core

E  105 GPa

25 mm

Fig. P2.33 and P2.34

4 ft

8 in.

Fig. P2.35

2.36 A 250-mm bar of 150 3 30-mm rectangular cross section consists

of two aluminum layers, 5 mm thick, brazed to a center brass layer

of the same thickness. If it is subjected to centric forces of magni-

tude P 5 30 kN, and knowing that E

5 70 GPa and E

5 105 GPa,

determine the normal stress (a) in the aluminum layers, (b) in the

brass layer.

Brass

Aluminum

5 mm

30 mm

5 mm

250 mm

Fig. P2.36

2.37 Determine the deformation of the composite bar of Prob. 2.36 if

it is subjected to centric forces of magnitude P 5 45 kN.

bee80288_ch02_052-139.indd Page 88 9/4/10 5:17:22 PM user-f499bee80288_ch02_052-139.indd Page 88 9/4/10 5:17:22 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02

Apago PDF Enhancer

Problems

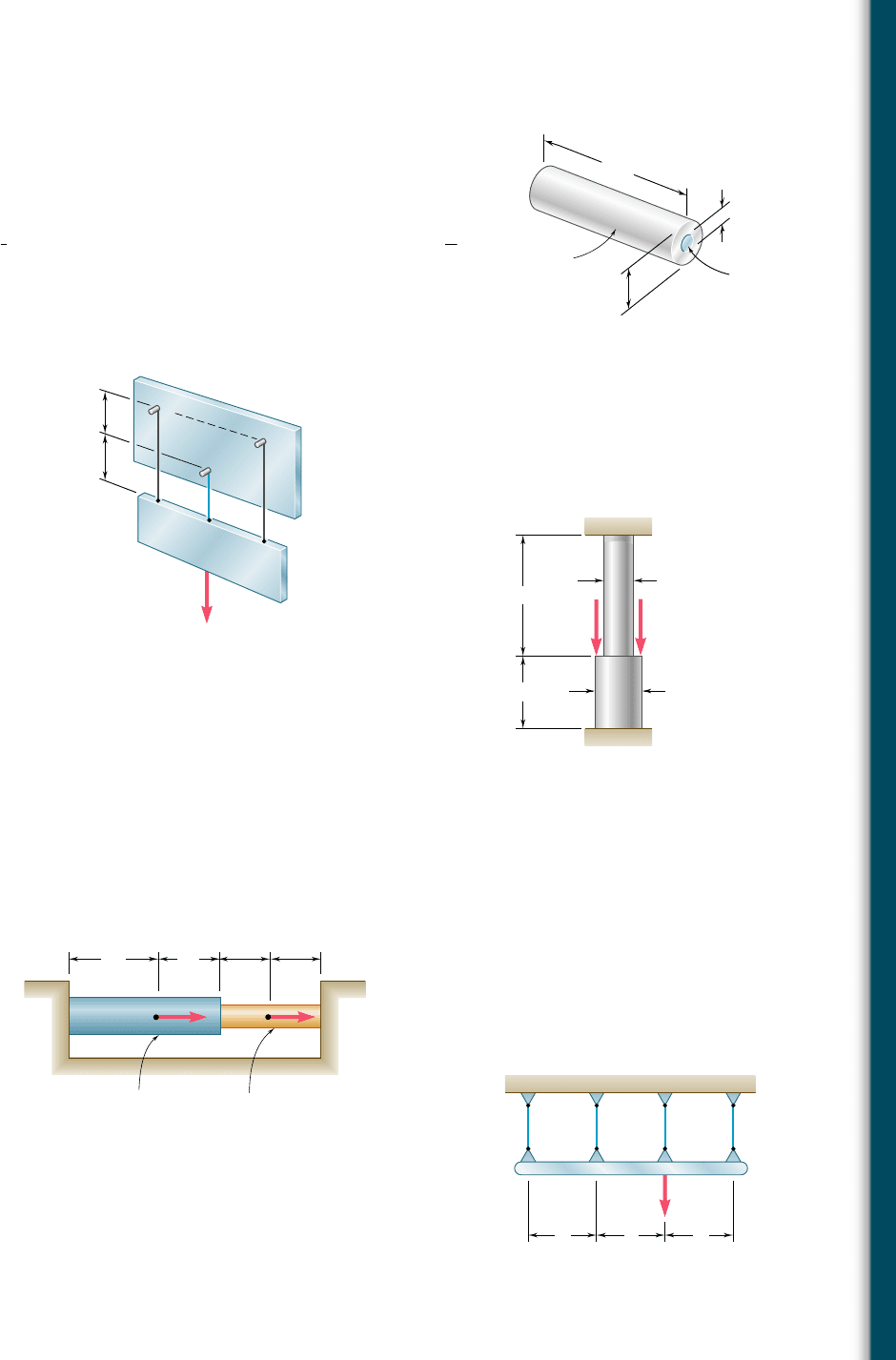
2.38 Compressive centric forces of 40 kips are applied at both ends

of the assembly shown by means of rigid end plates. Knowing that

5 29 3 10

psi and E

5 10.1 3 10

psi, determine (a) the

normal stresses in the steel core and the aluminum shell, (b) the

deformation of the assembly.

2.39 Three wires are used to suspend the plate shown. Aluminum wires

-in. diameter are used at A and B while a steel wire of

-in.

diameter is used at C. Knowing that the allowable stress for alu-

minum (E

5 10.4 3 10

psi) is 14 ksi and that the allowable stress

for steel (E

5 29 3 10

psi) is 18 ksi, determine the maximum load

P that can be applied.

Aluminum

shell

2.5 in.

10 in.

1 in.

Steel core

Fig. P2.38

Fig. P2.39

2.40 A polystyrene rod consisting of two cylindrical portions AB and BC

is restrained at both ends and supports two 6-kip loads as shown.

Knowing that E 5 0.45 3 10

psi, determine (a) the reactions at

A and C, (b) the normal stress in each portion of the rod.

2.41 Two cylindrical rods, one of steel and the other of brass, are joined

at C and restrained by rigid supports at A and E. For the loading

shown and knowing that E

5 200 GPa and E

5 105 GPa, deter-

mine (a) the reactions at A and E, (b) the deflection of point C.

15 in.

25 in.

1.25 in.

6 kips

2 in.

Fig. P2.40

180

40-mm diam. 30-mm diam.

120

100

Dimensions in mm

100

60 kN 40 kN

Brass

Steel

Fig. P2.41

2.42 Solve Prob. 2.41, assuming that rod AC is made of brass and rod

CE is made of steel.

2.43 The rigid bar ABCD is suspended from four identical wires. Deter-

mine the tension in each wire caused by the load P shown.

BC D

Fig. P2.43

bee80288_ch02_052-139.indd Page 89 9/4/10 5:17:29 PM user-f499bee80288_ch02_052-139.indd Page 89 9/4/10 5:17:29 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02

Apago PDF Enhancer

Stress and Strain—Axial Loading

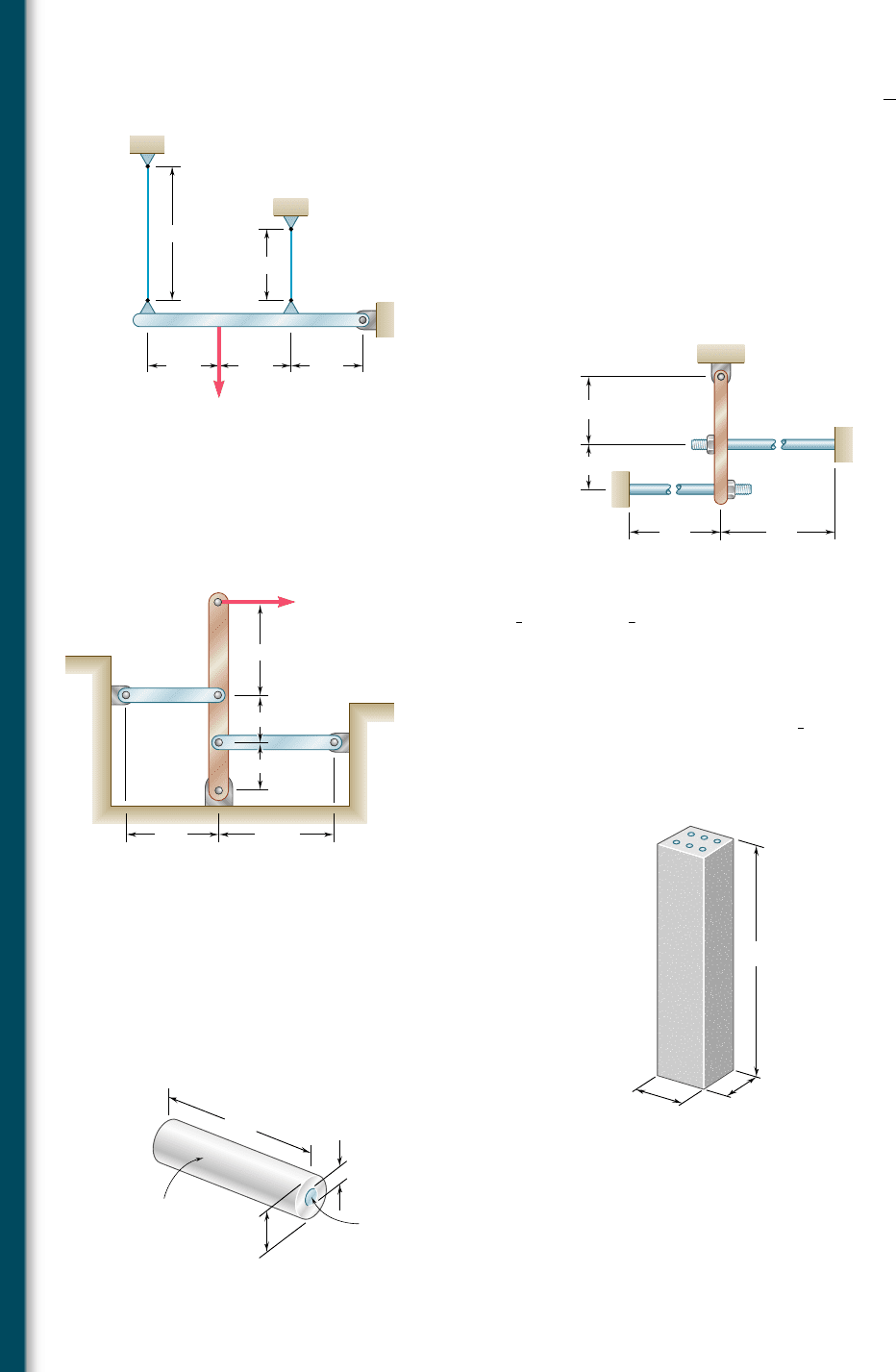
2.44 The rigid bar AD is supported by two steel wires of

-in. diameter

(E 5 29 3 10

psi) and a pin and bracket at D. Knowing that the

wires were initially taut, determine (a) the additional tension in

each wire when a 120-lb load P is applied at B, (b) the correspond-

ing deflection of point B.

2.45 The steel rods BE and CD each have a 16-mm diameter (E 5

200 GPa); the ends of the rods are single-threaded with a pitch

of 2.5 mm. Knowing that after being snugly fitted, the nut at C

is tightened one full turn, determine (a) the tension in rod CD,

(b) the deflection of point C of the rigid member ABC.

15 in.

8 in.8 in.8 in.

8 in.

Fig. P2.44

2.46 Links BC and DE are both made of steel (E 5 29 3 10

psi) and

are

in. wide and

in. thick. Determine (a) the force in each link

when a 600-lb force P is applied to the rigid member AF shown,

(b) the corresponding deflection of point A.

2.47 The concrete post (E

5 3.6 3 10

psi and a

5 5.5 3 10

/ 8F)

is reinforced with six steel bars, each of

-in diameter (E

5 29 3

psi and a

5 6.5 3 10

/ 8F). Determine the normal stresses

induced in the steel and in the concrete by a temperature rise

of 658F.

100 mm

2 m

3 m

150 mm

Fig. P2.45

5 in.4 in.

4 in.

2 in.

Fig. P2.46

6 ft

10 in.

Fig. P2.47

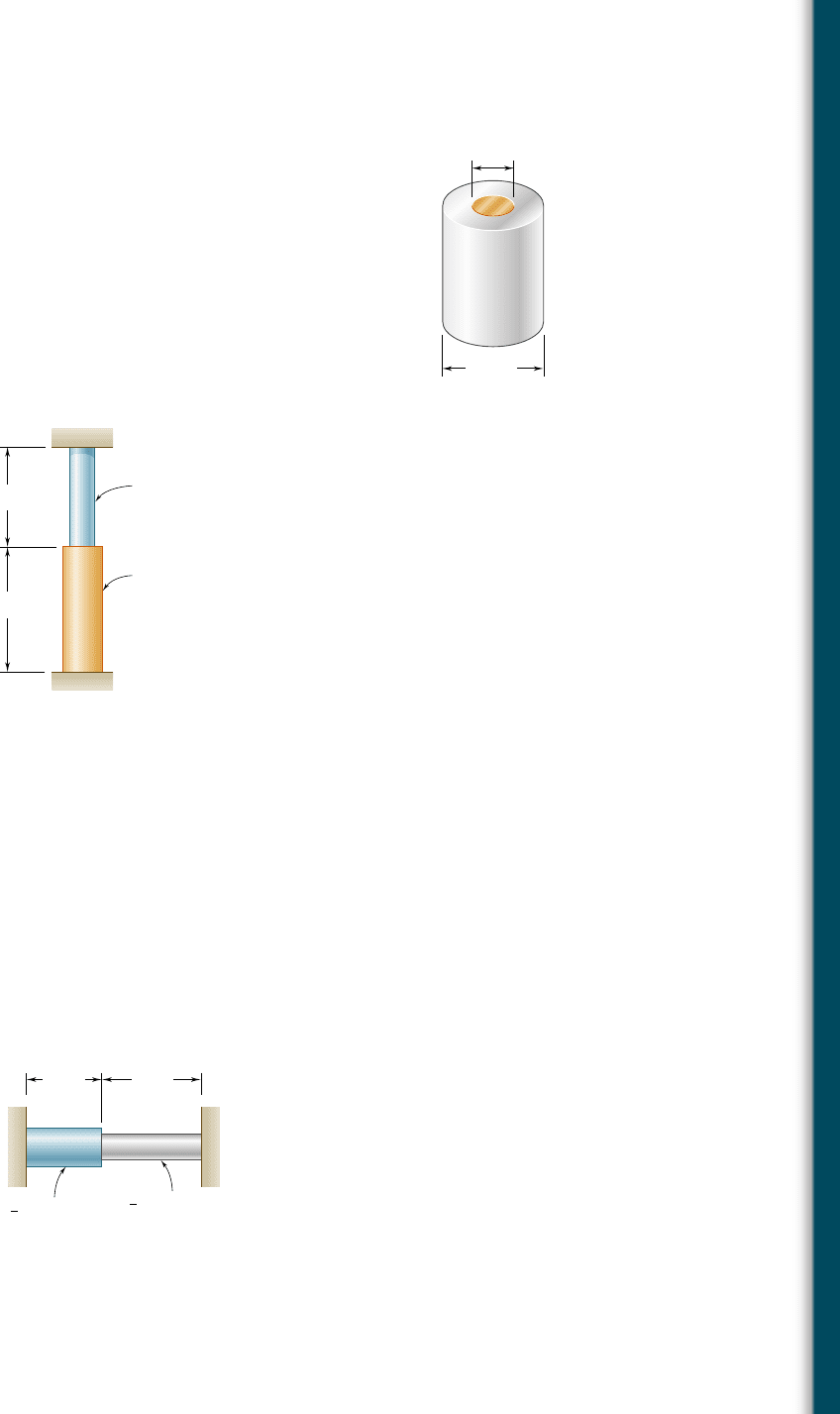
2.48 The assembly shown consists of an aluminum shell (E

5 10.6 3

psi, a

5 12.9 3 10

/8F) fully bonded to a steel core (E

29 3 10

psi, a

5 6.5 3 10

/8F) and is unstressed. Determine

(a) the largest allowable change in temperature if the stress in the

aluminum shell is not to exceed 6 ksi, (b) the corresponding change

in length of the assembly.

8 in.

Aluminum shell

1.25 in.

Steel

core

0.75 in.

Fig. P2.48

bee80288_ch02_052-139.indd Page 90 11/1/10 11:30:16 PM user-f499bee80288_ch02_052-139.indd Page 90 11/1/10 11:30:16 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02

Apago PDF Enhancer

Problems

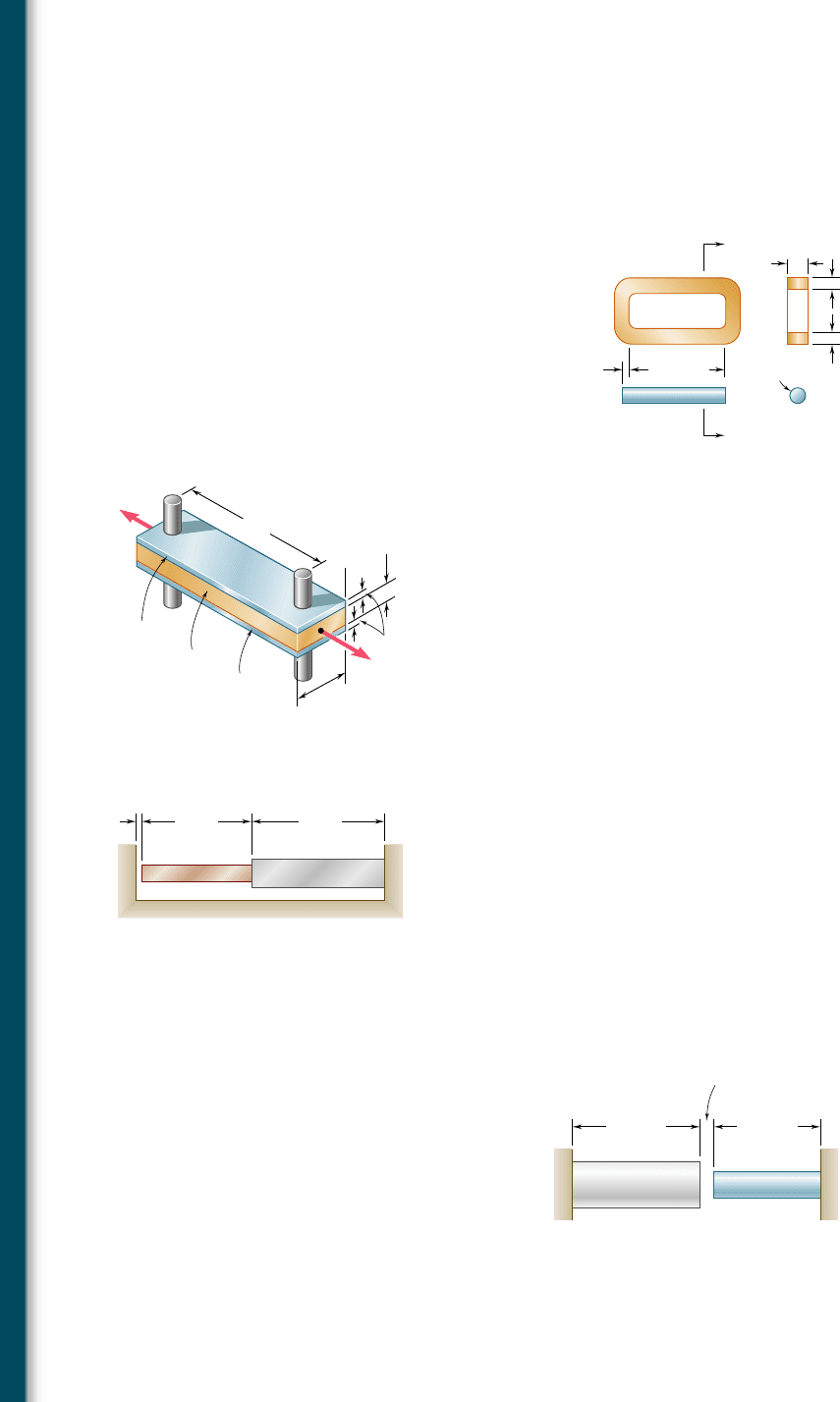
2.49 The aluminum shell is fully bonded to the brass core and the

assembly is unstressed at a temperature of 158C. Considering only

axial deformations, determine the stress in the aluminum when the

temperature reaches 1958C.

2.50 Solve Prob. 2.49, assuming that the core is made of steel (E

200 GPa, a

5 11.7 3 10

/8C) instead of brass.

2.51 A rod consisting of two cylindrical portions AB and BC is restrained

at both ends. Portion AB is made of steel (E

5 200 GPa, a

11.7 3 10

/8C) and portion BC is made of brass (E

5 105 GPa,

5 20.9 3 10

/8C). Knowing that the rod is initially unstressed,

determine the compressive force induced in ABC when there is a

temperature rise of 508C.

Brass core

E  105 GPa

 20.9  10

–6

/C

Aluminum shell

E  70 GPa

 23.6  10

–6

/C

25 mm

60 mm



Fig. P2.49

250 mm

300 mm

50-mm diamete

30-mm diamete

Fig. P2.51

2.52 A steel railroad track (E

5 200 GPa, a

5 11.7 3 10

/8C) was

laid out at a temperature of 68C. Determine the normal stress in

the rails when the temperature reaches 488C, assuming that the

rails (a) are welded to form a continuous track, (b) are 10 m long

with 3-mm gaps between them.

2.53 A rod consisting of two cylindrical portions AB and BC is restrained

at both ends. Portion AB is made of steel (E

5 29 3 10

psi,

5 6.5 3 10

/8F) and portion BC is made of aluminum (E

10.4 3 10

psi, a

5 13.3 3 10

/8F). Knowing that the rod is

initially unstressed, determine (a) the normal stresses induced in

portions AB and BC by a temperature rise of 708F, (b) the corre-

sponding deflection of point B.

1 -in. diamete

24 in. 32 in.

2 -in. diameter

Fig. P2.53

2.54 Solve Prob. 2.53, assuming that portion AB of the composite rod

is made of aluminum and portion BC is made of steel.

bee80288_ch02_052-139.indd Page 91 9/4/10 5:17:48 PM user-f499bee80288_ch02_052-139.indd Page 91 9/4/10 5:17:48 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02

Apago PDF Enhancer

Stress and Strain—Axial Loading

2.55 A brass link (E

5 105 GPa, a

5 20.9 3 10

/8C) and a steel rod

5 200 GPa, a

5 11.7 3 10

/8C) have the dimensions shown

at a temperature of 208C. The steel rod is cooled until it fits freely

into the link. The temperature of the whole assembly is then raised

to 458C. Determine (a) the final normal stress in the steel rod,

(b) the final length of the steel rod.

30-mm diameter

50 mm

250 mm0.12 mm

Steel

Section A-A

Brass

37.5 mm

Fig. P2.55

2.56 Two steel bars (E

5 200 GPa and a

5 11.7 3 10

/8C) are used

to reinforce a brass bar (E

5 105 GPa, a

5 20.9 3 10

/8C) that

is subjected to a load P 5 25 kN. When the steel bars were fabri-

cated, the distance between the centers of the holes that were to fit

on the pins was made 0.5 mm smaller than the 2 m needed. The steel

bars were then placed in an oven to increase their length so that they

would just fit on the pins. Following fabrication, the temperature in

the steel bars dropped back to room temperature. Determine (a) the

increase in temperature that was required to fit the steel bars on the

pins, (b) the stress in the brass bar after the load is applied to it.

2.57 Determine the maximum load P that can be applied to the brass

bar of Prob. 2.56 if the allowable stress in the steel bars is 30 MPa

and the allowable stress in the brass bar is 25 MPa.

2.58 Knowing that a 0.02-in. gap exists when the temperature is 758F,

determine (a) the temperature at which the normal stress in the

aluminum bar will be equal to 211 ksi, (b) the corresponding exact

length of the aluminum bar.

2.59 Determine (a) the compressive force in the bars shown after a

temperature rise of 1808F, (b) the corresponding change in length

of the bronze bar.

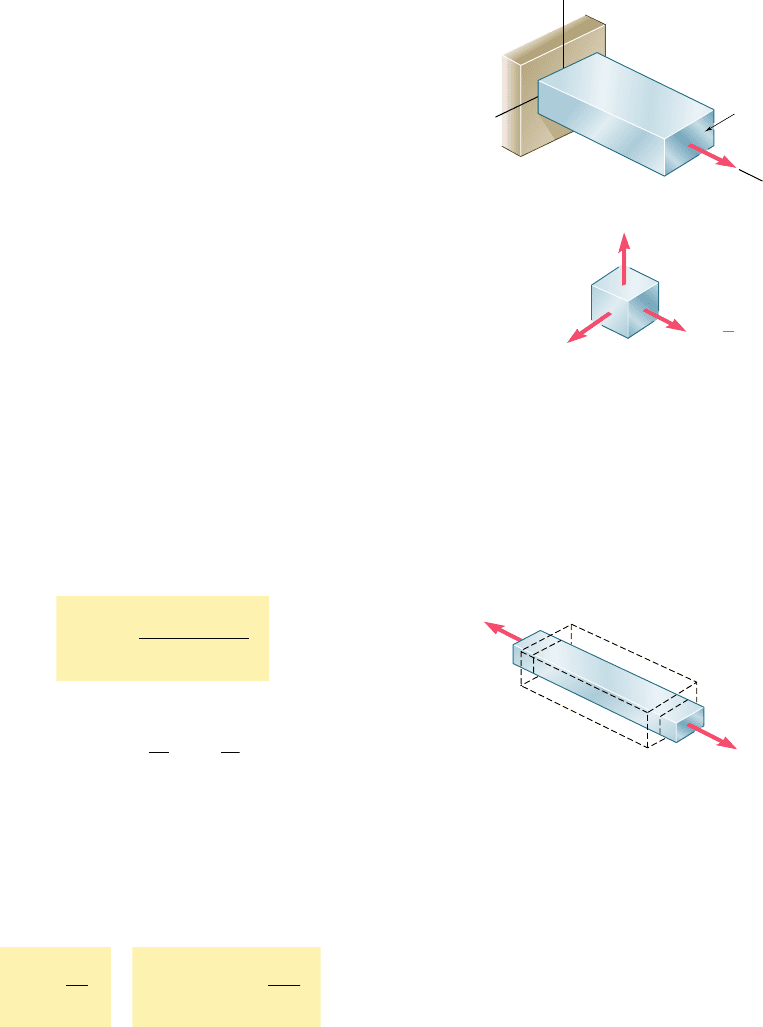
2.60 At room temperature (208C) a 0.5-mm gap exists between the ends

of the rods shown. At a later time when the temperature has

reached 1408C, determine (a) the normal stress in the aluminum

rod, (b) the change in length of the aluminum rod.

15 mm

40 mm

2 m

5 mm

Steel

Brass

Steel

P⬘

Fig. P2.56

Bronze

A  2.4 in

E  15  10

psi

 12  10

–6

/F

0.02 in.

14 in. 18 in.



Aluminum

A  2.8 in

E  10.6  10

psi

 12.9  10

–6

/F



Fig. P2.58 and P2.59

Aluminum

A  2000 mm

E  75

GPa

 23  16

–6

/C

300 mm 250 mm

0.5 mm



Stainless steel

A  800 mm

E  190 GPa

 17.3  10

–6

/C



Fig. P2.60

bee80288_ch02_052-139.indd Page 92 11/1/10 11:30:28 PM user-f499bee80288_ch02_052-139.indd Page 92 11/1/10 11:30:28 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02

Apago PDF Enhancer

2.11 POISSON’S RATIO

We saw in the earlier part of this chapter that, when a homogeneous

slender bar is axially loaded, the resulting stress and strain satisfy

Hooke’s law, as long as the elastic limit of the material is not exceeded.

Assuming that the load P is directed along the x axis (Fig. 2.35a),

we have s

5 PyA, where A is the cross-sectional area of the bar,

and, from Hooke’s law,

5 s

yE (2.24)

where E is the modulus of elasticity of the material.

We also note that the normal stresses on faces respectively per-

pendicular to the y and z axes are zero: s

5 s

5 0 (Fig. 2.35b). It

would be tempting to conclude that the corresponding strains P

and

are also zero. This, however, is not the case. In all engineering

materials, the elongation produced by an axial tensile force P in the

direction of the force is accompanied by a contraction in any trans-

verse direction (Fig. 2.36).† In this section and the following sections

(Secs. 2.12 through 2.15), all materials considered will be assumed to

be both homogeneous and isotropic, i.e., their mechanical properties

will be assumed independent of both position and direction. It follows

that the strain must have the same value for any transverse direction.

Therefore, for the loading shown in Fig. 2.35 we must have P

5 P

This common value is referred to as the lateral strain. An important

constant for a given material is its Poisson’s ratio, named after the

French mathematician Siméon Denis Poisson (1781–1840) and

denoted by the Greek letter n (nu). It is defined as

n 52

lateral strai

axial strain

(2.25)

n 52

(2.26)

for the loading condition represented in Fig. 2.35. Note the use of a

minus sign in the above equations to obtain a positive value for n, the

axial and lateral strains having opposite signs for all engineering mate-

rials.‡ Solving Eq. (2.26) for P

and P

, and recalling (2.24), we write

the following relations, which fully describe the condition of strain

under an axial load applied in a direction parallel to the x axis:

P

5 P

(2.27)

2.11 Poisson’s Ratio

†It would also be tempting, but equally wrong, to assume that the volume of the rod

remains unchanged as a result of the combined effect of the axial elongation and transverse

contraction (see Sec. 2.13).

‡However, some experimental materials, such as polymer foams, expand laterally when

stretched. Since the axial and lateral strains have then the same sign, the Poisson’s ratio

of these materials is negative. (See Roderic Lakes, “Foam Structures with a Negative

Poisson’s Ratio,” Science, 27 February 1987, Volume 235, pp. 1038–1040.)

(a)

(b)

␴

⫽

␴

⫽

␴

⫽

Fig. 2.35 Stresses in an axially-

loaded bar.

Fig. 2.36 Transverse contraction

of bar under axial tensile force.

bee80288_ch02_052-139.indd Page 93 11/8/10 8:06:36 PM user-f499bee80288_ch02_052-139.indd Page 93 11/8/10 8:06:36 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02

Apago PDF Enhancer

2.12 MULTIAXIAL LOADING; GENERALIZED

HOOKE’S LAW

All the examples considered so far in this chapter have dealt with

slender members subjected to axial loads, i.e., to forces directed

along a single axis. Choosing this axis as the x axis, and denoting by

P the internal force at a given location, the corresponding stress

components were found to be s

5 PyA, s

5 0, and s

5 0.

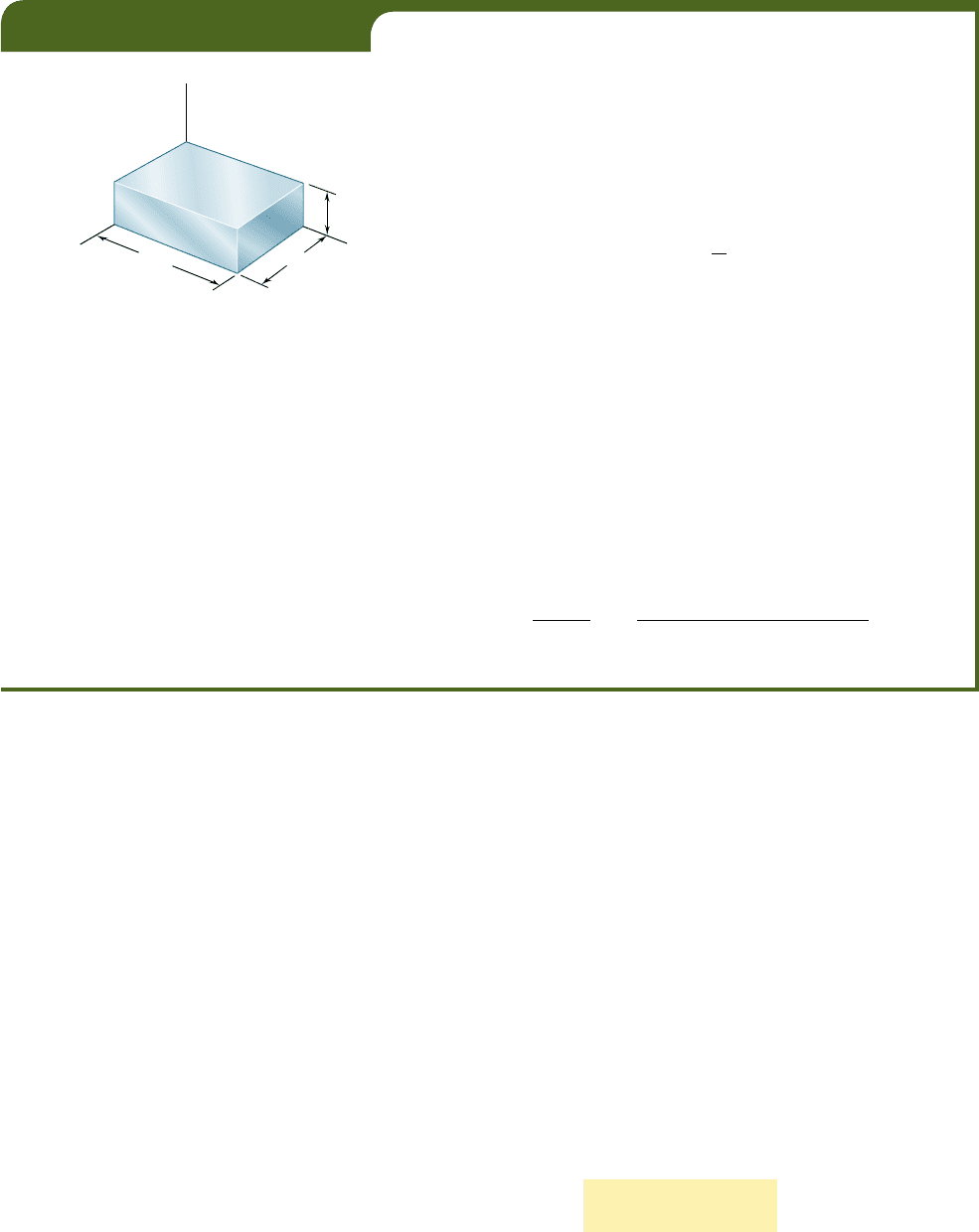
Let us now consider structural elements subjected to loads

acting in the directions of the three coordinate axes and producing

normal stresses s

, s

, and s

which are all different from zero

(Fig. 2.38). This condition is referred to as a multiaxial loading.

Note that this is not the general stress condition described in Sec.

1.12, since no shearing stresses are included among the stresses

shown in Fig. 2.38.

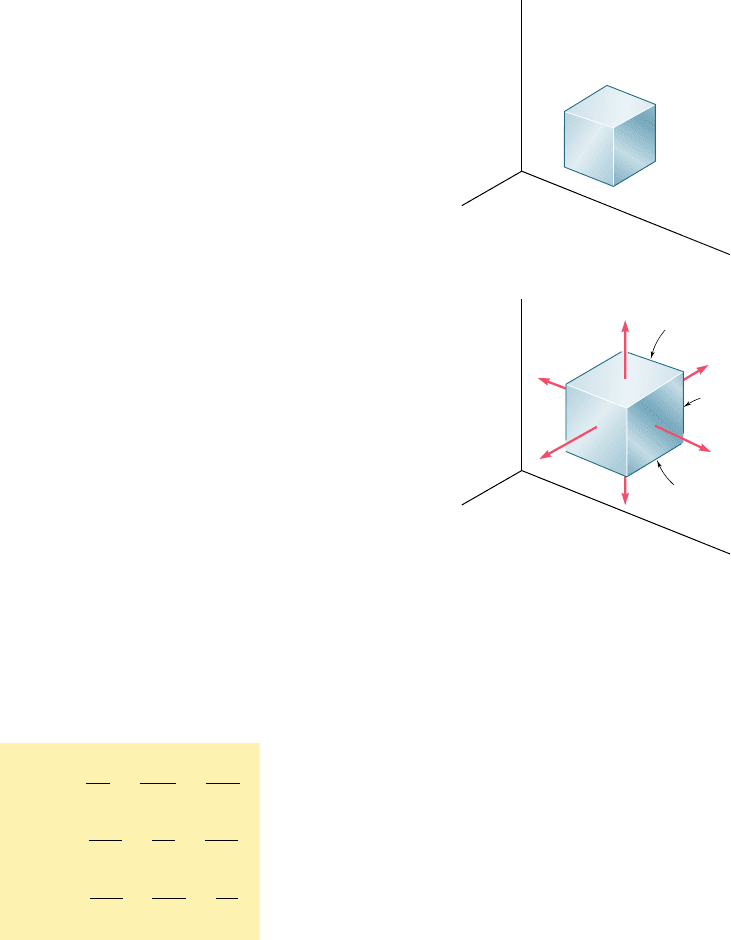
Consider an element of an isotropic material in the shape of a

cube (Fig. 2.39a). We can assume the side of the cube to be equal

to unity, since it is always possible to select the side of the cube as

a unit of length. Under the given multiaxial loading, the element will

deform into a rectangular parallelepiped of sides equal, respectively,

to 1 1 P

, 1 1 P

, and 1 1 P

, where P

, P

, and P

denote the values

of the normal strain in the directions of the three coordinate axes

(Fig. 2.39b). You should note that, as a result of the deformations of

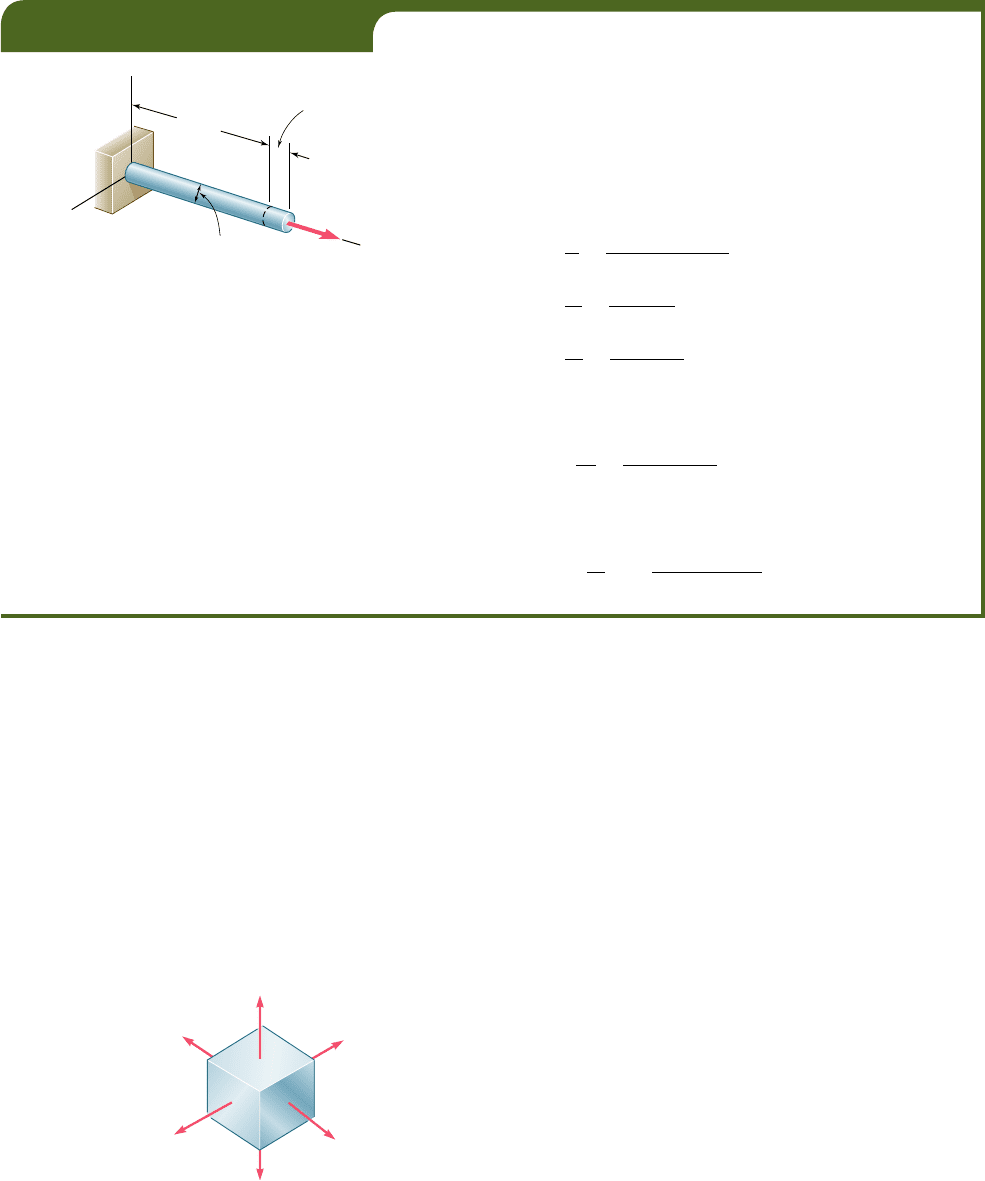
A 500-mm-long, 16-mm-diameter rod made of a homogenous, isotropic

material is observed to increase in length by 300 mm, and to decrease in

diameter by 2.4 mm when subjected to an axial 12-kN load. Determine

the modulus of elasticity and Poisson’s ratio of the material.

The cross-sectional area of the rod is

A 5 pr

5 p18 3 10

5 201 3 10

Choosing the x axis along the axis of the rod (Fig. 2.37), we write

12 3 10

201 3 10

5 59.7 MPa

300 m

500 mm

5 600 3 10

22.4 m

16 mm

52150 3 10

From Hooke’s law, s

5 EP

, we obtain

E 5

59.7 MPa

600 3 10

5 99.5 GPa

and, from Eq. (2.26),

n 52

2150 3 10

600 3 10

5 0.25

EXAMPLE 2.07

12 kN

⫽ 500 mm

⫽ 16 mm

␮␦

⫽ – 2.4

␮

␦

⫽ 300

Fig. 2.37

␴

Fig. 2.38 Stress state for

multiaxial loading.

bee80288_ch02_052-139.indd Page 94 11/8/10 9:32:56 PM user-f494bee80288_ch02_052-139.indd Page 94 11/8/10 9:32:56 PM user-f494 volume 201/FREE048/work%0/indd%0/volume 201/FREE048/work%0/indd%0/

Apago PDF Enhancer

the other elements of the material, the element under consideration

could also undergo a translation, but we are concerned here only

with the actual deformation of the element, and not with any possible

superimposed rigid-body displacement.

In order to express the strain components P

, P

in terms of

the stress components s

, s

, we will consider separately the

effect of each stress component and combine the results obtained.

The approach we propose here will be used repeatedly in this text,

and is based on the principle of superposition. This principle states

that the effect of a given combined loading on a structure can be

obtained by determining separately the effects of the various loads

and combining the results obtained, provided that the following con-

ditions are satisfied:

1. Each effect is linearly related to the load that produces it.

2. The deformation resulting from any given load is small and does

not affect the conditions of application of the other loads.

In the case of a multiaxial loading, the first condition will be

satisfied if the stresses do not exceed the proportional limit of the

material, and the second condition will also be satisfied if the stress

on any given face does not cause deformations of the other faces that

are large enough to affect the computation of the stresses on those

faces.

Considering first the effect of the stress component s

, we recall

from Sec. 2.11 that s

causes a strain equal to s

yE in the x direc-

tion, and strains equal to 2ns

yE in each of the y and z directions.

Similarly, the stress component s

, if applied separately, will cause a

strain s

yE in the y direction and strains 2ns

yE in the other two

directions. Finally, the stress component s

causes a strain s

yE in

the z direction and strains 2ns

yE in the x and y directions. Com-

bining the results obtained, we conclude that the components of

strain corresponding to the given multiaxial loading are

(2.28)

The relations (2.28) are referred to as the generalized Hooke’s

law for the multiaxial loading of a homogeneous isotropic material.

As we indicated earlier, the results obtained are valid only as long as

the stresses do not exceed the proportional limit, and as long as the

deformations involved remain small. We also recall that a positive

value for a stress component signifies tension, and a negative value

compression. Similarly, a positive value for a strain component indi-

cates expansion in the corresponding direction, and a negative value

contraction.

2.12 Multiaxial Loading; Generalized

Hooke’s Law

(a)

␴

⑀

␴

(b)

⫹

⑀

⫹

⑀

⫹

Fig. 2.39 Deformation of cube under

multiaxial loading.

bee80288_ch02_052-139.indd Page 95 11/8/10 8:06:59 PM user-f499bee80288_ch02_052-139.indd Page 95 11/8/10 8:06:59 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02

Apago PDF Enhancer

*2.13 DILATATION; BULK MODULUS

In this section you will examine the effect of the normal stresses s

, and s

on the volume of an element of isotropic material. Con-

sider the element shown in Fig. 2.39. In its unstressed state, it is in

the shape of a cube of unit volume; and under the stresses s

, s

, it deforms into a rectangular parallelepiped of volume

v 5 (1 1 P

)(1 1 P

)

Since the strains P

, P

are much smaller than unity, their products

will be even smaller and may be omitted in the expansion of the

product. We have, therefore,

v 5 1 1 P

1 P

Denoting by e the change in volume of our element, we write

e 5 v 2 1 5 1 1 P

1 P

2 1

e 5 P

1 P

(2.30)

The steel block shown (Fig. 2.40) is subjected to a uniform pressure on

all its faces. Knowing that the change in length of edge AB is 21.2 3

in., determine (a) the change in length of the other two edges,

(b) the pressure p applied to the faces of the block. Assume E 5 29 3

psi and n 5 0.29.

(a) Change in Length of Other Edges. Substituting s

5 s

5 2p into the relations (2.28), we find that the three strain compo-

nents have the common value

5 P

11 2 2n2

(2.29)

Since

5 d

AB 5

21.2 3 10

in.

4 in.

52300 3 10

in./in.

we obtain

5 P

52300 3 10

in./in.

from which it follows that

5 P

1BC25 12300 3 10

212 in.252600 3 10

in.

5 P

1BD25 12300 3 10

213 in.252900 3 10

in.

(b) Pressure. Solving Eq. (2.29) for p, we write

p 52

1 2 2n

129 3 10

psi212300 3 10

1 2 0.58

p 5 20.7 ksi

EXAMPLE 2.08

2 in.

3 in.

4 in.

Fig. 2.40

bee80288_ch02_052-139.indd Page 96 11/8/10 8:07:08 PM user-f499bee80288_ch02_052-139.indd Page 96 11/8/10 8:07:08 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02