Beer F.P., Johnston E.R., DeWolf J.T., Mazurek D.F. Mechanics of Materials
Подождите немного. Документ загружается.

Apago PDF Enhancer
77
Problems
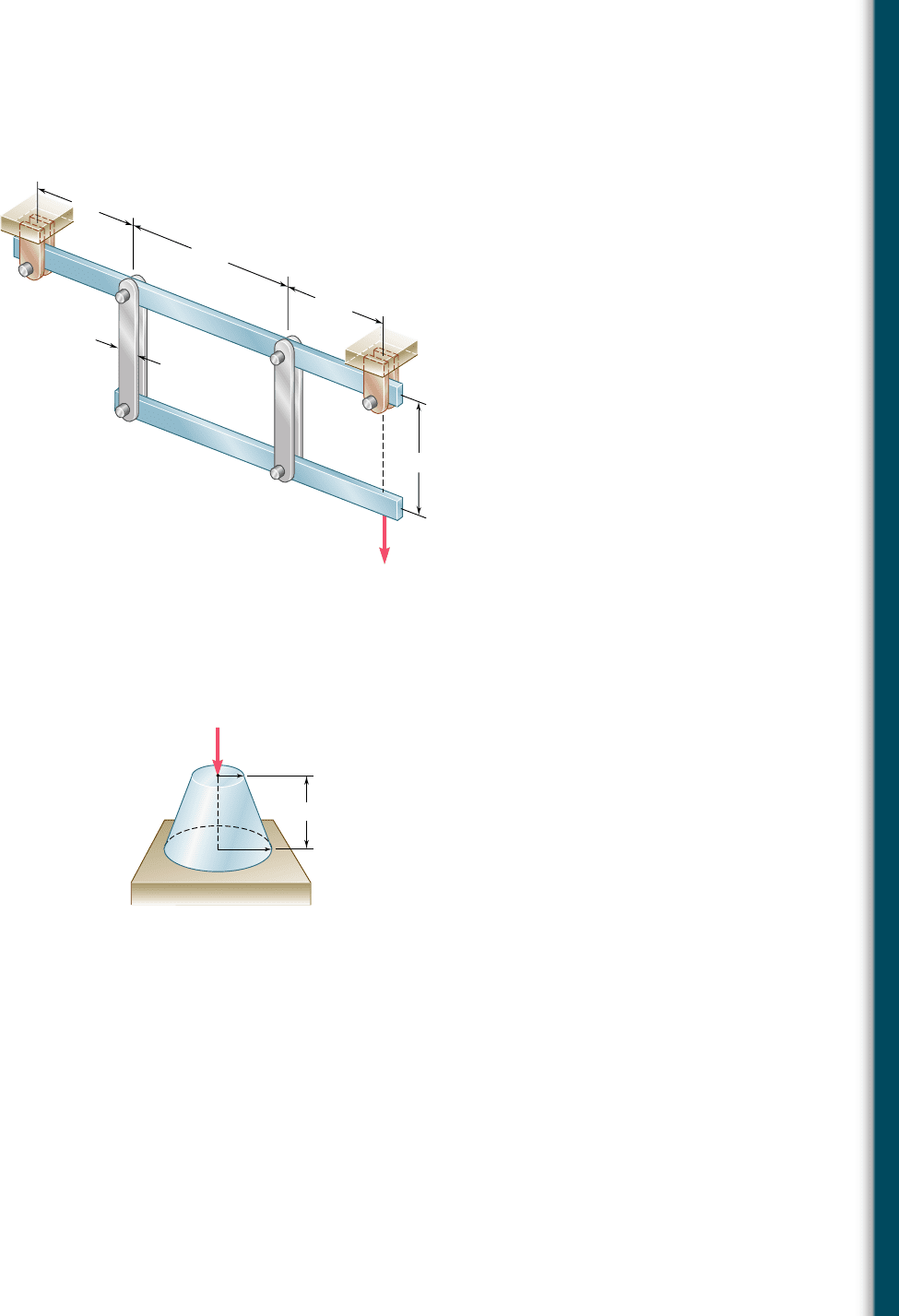
2.28 Each of the four vertical links connecting the two rigid horizontal
members is made of aluminum (E 5 70 GPa) and has a uniform
rectangular cross section of 10 3 40 mm. For the loading shown,
determine the deflection of (a) point E, (b) point F, (c) point G.
24 kN
F
E
A
B
C
D
300 mm
250 mm
400 mm
250 mm
40 mm
G
Fig. P2.28
h
A
a
b
P
Fig. P2.29
2.29 The vertical load P is applied at the center A of the upper section
of a homogeneous frustum of a circular cone of height h, minimum
radius a, and maximum radius b. Denoting by E the modulus of
elasticity of the material and neglecting the effect of its weight,
determine the deflection of point A.
2.30 A homogenous cable of length L and uniform cross section is sus-
pended from one end. (a) Denoting by r the density (mass per unit
volume) of the cable and by E its modulus of elasticity, determine
the elongation of the cable due to its own weight. (b) Show that the
same elongation would be obtained if the cable were horizontal and
if a force equal to half of its weight were applied at each end.
2.31 The volume of a tensile specimen is essentially constant while
plastic deformation occurs. If the initial diameter of the specimen
is d
1
, show that when the diameter is d, the true strain is
P
t
5 2 ln(d
1
yd).
2.32 Denoting by P the “engineering strain” in a tensile specimen, show
that the true strain is P
t
5 ln(1 1 P).
bee80288_ch02_052-139.indd Page 77 9/4/10 5:16:31 PM user-f499bee80288_ch02_052-139.indd Page 77 9/4/10 5:16:31 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02
Apago PDF Enhancer
78
Stress and Strain—Axial Loading
2.9 STATICALLY INDETERMINATE PROBLEMS
In the problems considered in the preceding section, we could always
use free-body diagrams and equilibrium equations to determine the
internal forces produced in the various portions of a member under
given loading conditions. The values obtained for the internal forces
were then entered into Eq. (2.8) or (2.9) to obtain the deformation
of the member.
There are many problems, however, in which the internal forces
cannot be determined from statics alone. In fact, in most of these
problems the reactions themselves—which are external forces—
cannot be determined by simply drawing a free-body diagram of the
member and writing the corresponding equilibrium equations. The
equilibrium equations must be complemented by relations involving
deformations obtained by considering the geometry of the problem.
Because statics is not sufficient to determine either the reactions or
the internal forces, problems of this type are said to be statically
indeterminate. The following examples will show how to handle this
type of problem.
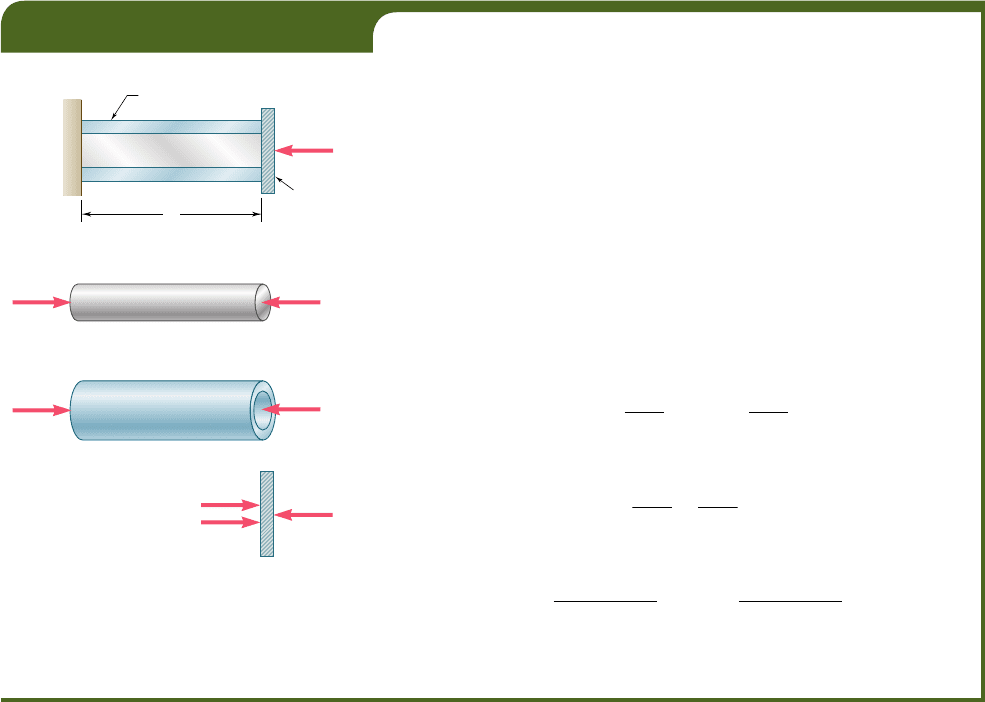
A rod of length L, cross-sectional area A
1
, and modulus of elasticity E
1
,
has been placed inside a tube of the same length L, but of cross-sectional
area A
2
and modulus of elasticity E
2
(Fig. 2.21a). What is the deformation
of the rod and tube when a force P is exerted on a rigid end plate as
shown?
Denoting by P
1
and P
2
, respectively, the axial forces in the rod and
in the tube, we draw free-body diagrams of all three elements (Fig. 2.21b,
c, d). Only the last of the diagrams yields any significant information,
namely:
P
1
1 P
2
5 P (2.11)
Clearly, one equation is not sufficient to determine the two unknown
internal forces P
1
and P
2
. The problem is statically indeterminate.
However, the geometry of the problem shows that the deformations
d
1
and d
2
of the rod and tube must be equal. Recalling Eq. (2.7), we
write
d
1
5
P
1
L
A
1
E
1
d
2
5
P
2
L
A
2
E
2
(2.12)
Equating the deformations d
1
and d
2
, we obtain:
P
1
A
1
E
1
5
P
2
A
2
E
2
(2.13)
Equations (2.11) and (2.13) can be solved simultaneously for P
1
and P
2
:
P
1
5
A
1
E
1
P
A
1
E
1
1 A
2
E
2
P
2
5
A
2
E
2
P
A
1
E
1
1 A
2
E
2
Either of Eqs. (2.12) can then be used to determine the common defor-
mation of the rod and tube.
EXAMPLE 2.02
P
P
1
P'
1
Tube (A
2
, E
2
)
Rod (A
1
, E
1
)
End plate
(a)
(b)
(c)
(d)
L
P'
2
P
2
P
P
1
P
2
Fig. 2.21
bee80288_ch02_052-139.indd Page 78 9/4/10 5:16:36 PM user-f499bee80288_ch02_052-139.indd Page 78 9/4/10 5:16:36 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02

Apago PDF Enhancer
Superposition Method. We observe that a structure is statically
indeterminate whenever it is held by more supports than are required
to maintain its equilibrium. This results in more unknown reactions
than available equilibrium equations. It is often found convenient to
designate one of the reactions as redundant and to eliminate the
corresponding support. Since the stated conditions of the problem
cannot be arbitrarily changed, the redundant reaction must be main-
tained in the solution. But it will be treated as an unknown load that,
together with the other loads, must produce deformations that are
compatible with the original constraints. The actual solution of the
problem is carried out by considering separately the deformations
caused by the given loads and by the redundant reaction, and by
adding—or superposing—the results obtained.†
79
EXAMPLE 2.03
A bar AB of length L and uniform cross section is attached to rigid sup-
ports at A and B before being loaded. What are the stresses in portions
AC and BC due to the application of a load P at point C (Fig. 2.22a)?
Drawing the free-body diagram of the bar (Fig. 2.22b), we obtain
the equilibrium equation
R
A
1 R
B
5 P (2.14)
Since this equation is not sufficient to determine the two unknown reac-
tions R
A
and R
B
, the problem is statically indeterminate.
However, the reactions may be determined if we observe from the
geometry that the total elongation d of the bar must be zero. Denoting
by d
1
and d
2
, respectively, the elongations of the portions AC and BC, we
write
d 5 d
1
1 d
2
5 0
or, expressing d
1
and d
2
in terms of the corresponding internal forces P
1
and P
2
:
d 5
P
1
L
1
AE
1
P
2
L
2
AE
5 0
(2.15)
But we note from the free-body diagrams shown respectively in parts b
and c of Fig. 2.23 that P
1
5 R
A
and P
2
5 2R
B
. Carrying these values into
(2.15), we write
R
A
L
1
2 R
B
L
2
5 0 (2.16)
Equations (2.14) and (2.16) can be solved simultaneously for R
A
and R
B
;
we obtain R
A
5 PL
2
yL and R
B
5 PL
1
yL. The desired stresses s
1
in AC
and s
2
in BC are obtained by dividing, respectively, P
1
5 R
A
and P
2
5
2R
B
by the cross-sectional area of the bar:
s
1
5
P
L
2
AL
s
2
52
P
L
1
AL
†
The general conditions under which the combined effect of several loads can be obtained
in this way are discussed in Sec. 2.12.
P
L
1
L
2
R
A
R
B
(a)(b)
L
A
B
A
B
CC
P
Fig. 2.22
R
A
P
R
A
R
B
R
B
(a)
(b)
(c)
A
B
C
P
1
P
2
Fig. 2.23
bee80288_ch02_052-139.indd Page 79 11/8/10 8:06:10 PM user-f499bee80288_ch02_052-139.indd Page 79 11/8/10 8:06:10 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02
Apago PDF Enhancer
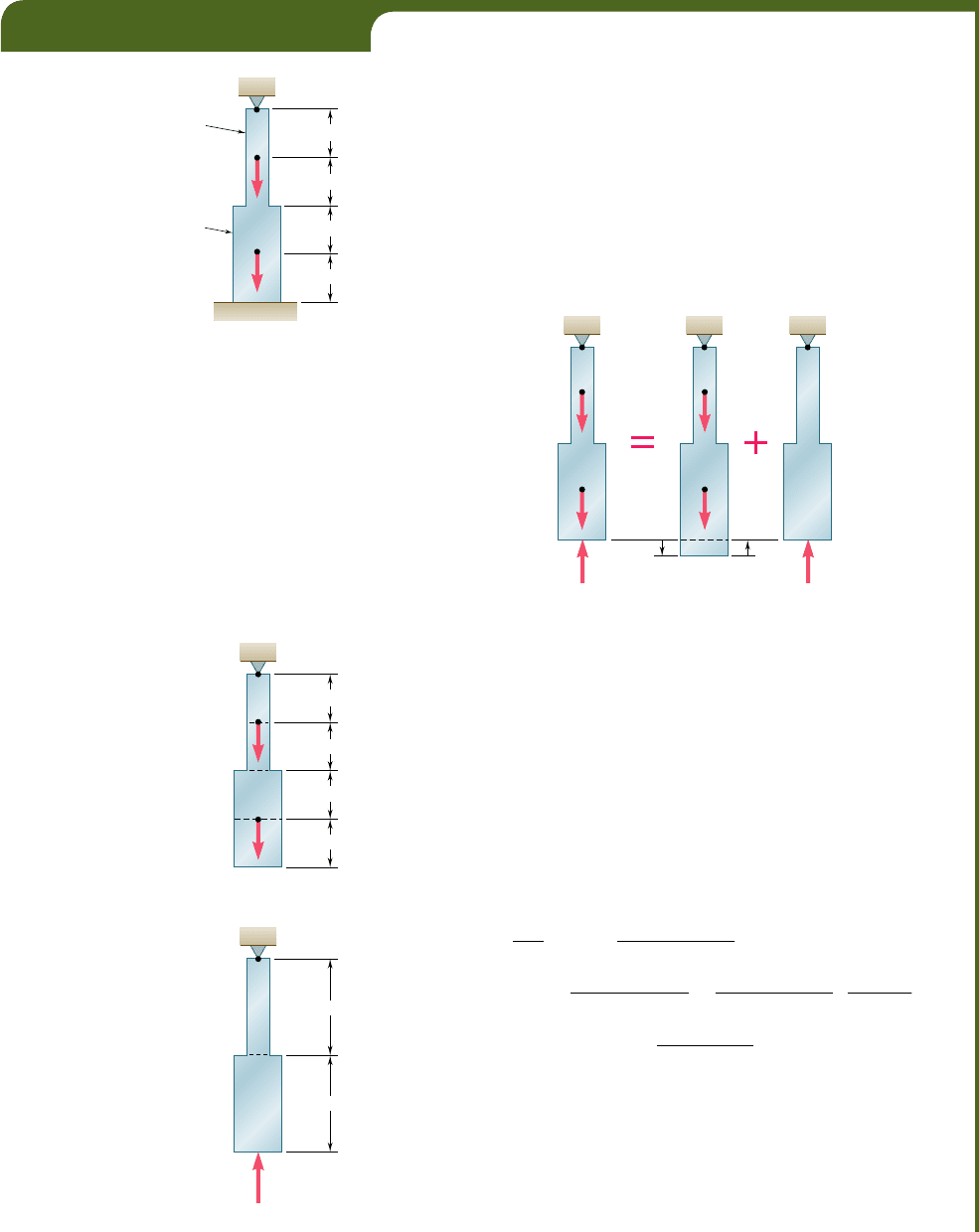
EXAMPLE 2.04
Determine the reactions at A and B for the steel bar and loading shown
in Fig. 2.24, assuming a close fit at both supports before the loads are
applied.
We consider the reaction at B as redundant and release the bar
from that support. The reaction R
B
is now considered as an unknown
load (Fig. 2.25a) and will be determined from the condition that the
deformation d of the rod must be equal to zero. The solution is carried
out by considering separately the deformation d
L
caused by the given
loads (Fig. 2.25b) and the deformation d
R
due to the redundant reaction
R
B
(Fig. 2.25c).
C
A
D
K
B
A
⫽ 250 mm
2
A
⫽ 400 mm
2
300 kN
600 kN
150 mm
150 mm
150 mm
150 mm
Fig. 2.24
A
300 kN
600 kN
A
300 kN
600 kN
A
L
␦␦
R
␦
(a)(b)(c)
⫽ 0
R
B
R
B
Fig. 2.25
C
K
D
3
4
2
1
A
B
300 kN
600 kN
150 mm
150 mm
150 mm
150 mm
Fig. 2.26
The deformation d
L
is obtained from Eq. (2.8) after the bar has
been divided into four portions, as shown in Fig. 2.26. Following the same
procedure as in Example 2.01, we write
P
1
5 0P
2
5 P
3
5 600 3 10
3
NP
4
5 900 3 10
3
N
A
1
5 A
2
5 400 3 10
26
m
2
A
3
5 A
4
5 250 3 10
26
m
2
L
1
5 L
2
5 L
3
5 L
4
5 0.150 m
Substituting these values into Eq. (2.8), we obtain
d
L
5
a
4
i51
P
i
L
i
A
i
E
5 a0 1
600 3 10
3
N
400 3 10
26
m
2
1
600 3 10
3
N
250 3 10
26
m
2
1
900 3 10
3
N
250 3 10
26
m
2
b
0.150 m
E
d
L
5
1.125 3 10
9
E
(2.17)
Considering now the deformation d
R
due to the redundant reaction
R
B
, we divide the bar into two portions, as shown in Fig. 2.27, and
write
P
1
5 P
2
5 2R
B
A
1
5 400 3 10
26
m
2
A
2
5 250 3 10
26
m
2
L
1
5 L
2
5 0.300 m
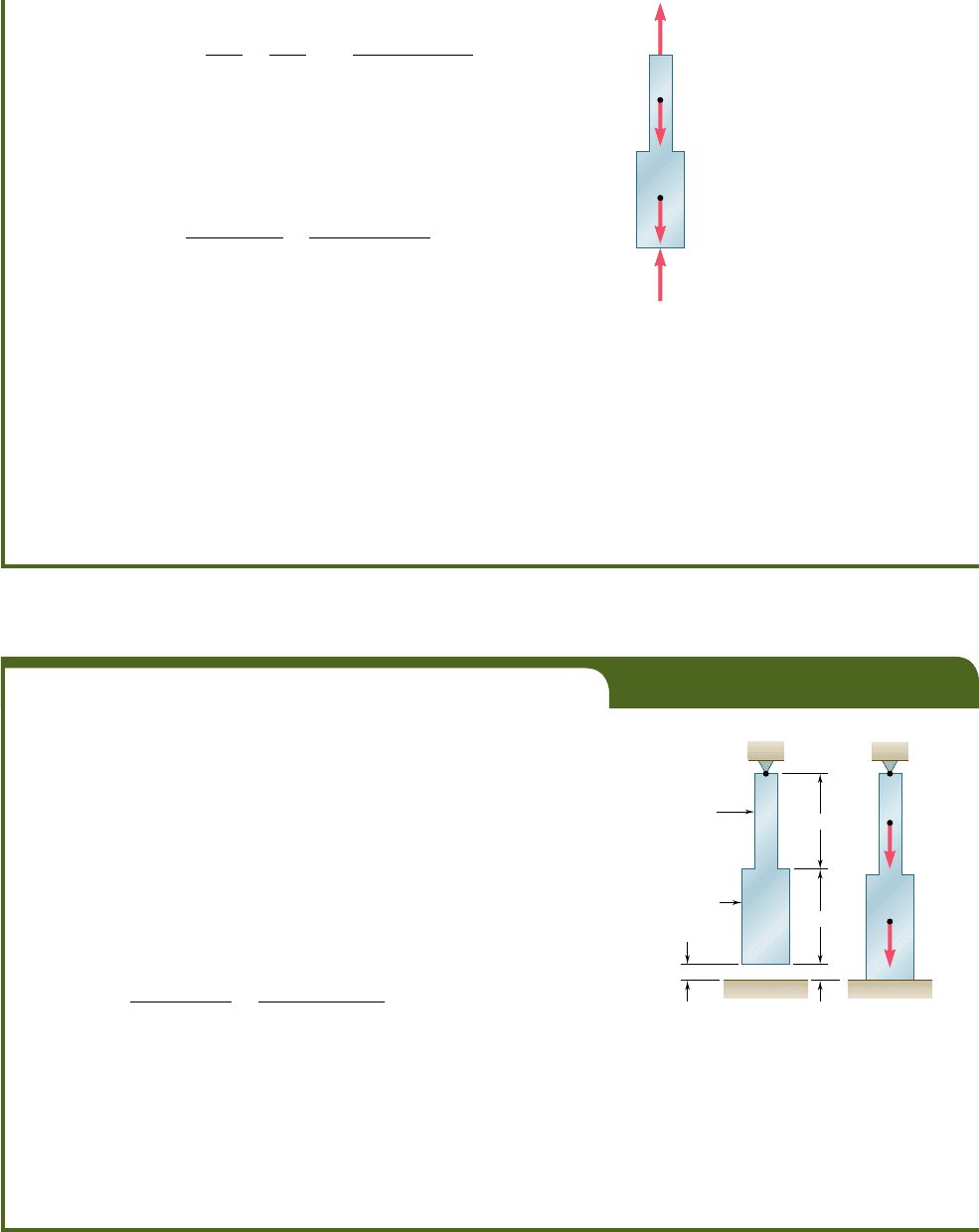
80
C
1
2
A
B
R
B
300 mm
300 mm
Fig. 2.27
bee80288_ch02_052-139.indd Page 80 9/4/10 5:16:44 PM user-f499bee80288_ch02_052-139.indd Page 80 9/4/10 5:16:44 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02
Apago PDF Enhancer
81
Substituting these values into Eq. (2.8), we obtain
d
R
5
P
1
L
1
A
1
E
1
P
2
L
2
A
2
E
52
11.95 3 10
3
2R
B
E
(2.18)
Expressing that the total deformation d of the bar must be zero, we
write
d 5 d
L
1 d
R
5 0 (2.19)
and, substituting for d
L
and d
R
from (2.17) and (2.18) into (2.19),
d 5
1.125 3 10
9
E
2
11.95 3 10
3
2R
B
E
5 0
Solving for R
B
, we have
R
B
5 577 3 10
3
N 5 577 kN
The reaction R
A
at the upper support is obtained from the free-
body diagram of the bar (Fig. 2.28). We write
1
c o F
y
5 0:R
A
2 300 kN 2 600 kN 1 R
B
5 0
R
A
5 900
k
N 2 R
B
5 900
k
N 2 577
k
N 5 323
k
N
Once the reactions have been determined, the stresses and strains
in the bar can easily be obtained. It should be noted that, while the total
deformation of the bar is zero, each of its component parts does deform
under the given loading and restraining conditions.
C
A
300 kN
600 kN
B
R
B
R
A
Fig. 2.28
EXAMPLE 2.05
Determine the reactions at A and B for the steel bar and loading of
Example 2.04, assuming now that a 4.50-mm clearance exists between the
bar and the ground before the loads are applied (Fig. 2.29). Assume E 5
200 GPa.
We follow the same procedure as in Example 2.04. Considering the
reaction at B as redundant, we compute the deformations d
L
and d
R
caused, respectively, by the given loads and by the redundant reaction R
B
.
However, in this case the total deformation is not zero, but d 5 4.5 mm.
We write therefore
d 5 d
L
1 d
R
5 4.5 3 10
23
m (2.20)
Substituting for d
L
and d
R
from (2.17) and (2.18) into (2.20), and recalling
that E 5 200 GPa 5 200 3 10
9
Pa, we have
d 5
1.125 3 10
9
2
00
3
10
9
2
11.95 3 10
3
2R
B
2
00
3
10
9
5 4.5 3 10
23
m
Solving for R
B
, we obtain
R
B
5 115.4 3 10
3
N 5 115.4 kN
The reaction at A is obtained from the free-body diagram of the bar
(Fig. 2.28):
1
c o F
y
5 0:R
A
2 300 kN 2 600 kN 1 R
B
5 0
R
A
5 900
k
N 2 R
B
5 900
k
N 2 115.4
k
N 5 785
k
N
C
C
AA
BB
300 kN
600 kN
300 mm
4.5 mm
300 mm
A
⫽ 250 mm
2
A
⫽ 400 mm
2
␦
Fig. 2.29
bee80288_ch02_052-139.indd Page 81 11/8/10 8:06:22 PM user-f499bee80288_ch02_052-139.indd Page 81 11/8/10 8:06:22 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02
Apago PDF Enhancer
82
Stress and Strain—Axial Loading
2.10 PROBLEMS INVOLVING TEMPERATURE CHANGES
All of the members and structures that we have considered so far
were assumed to remain at the same temperature while they were
being loaded. We are now going to consider various situations involv-
ing changes in temperature.
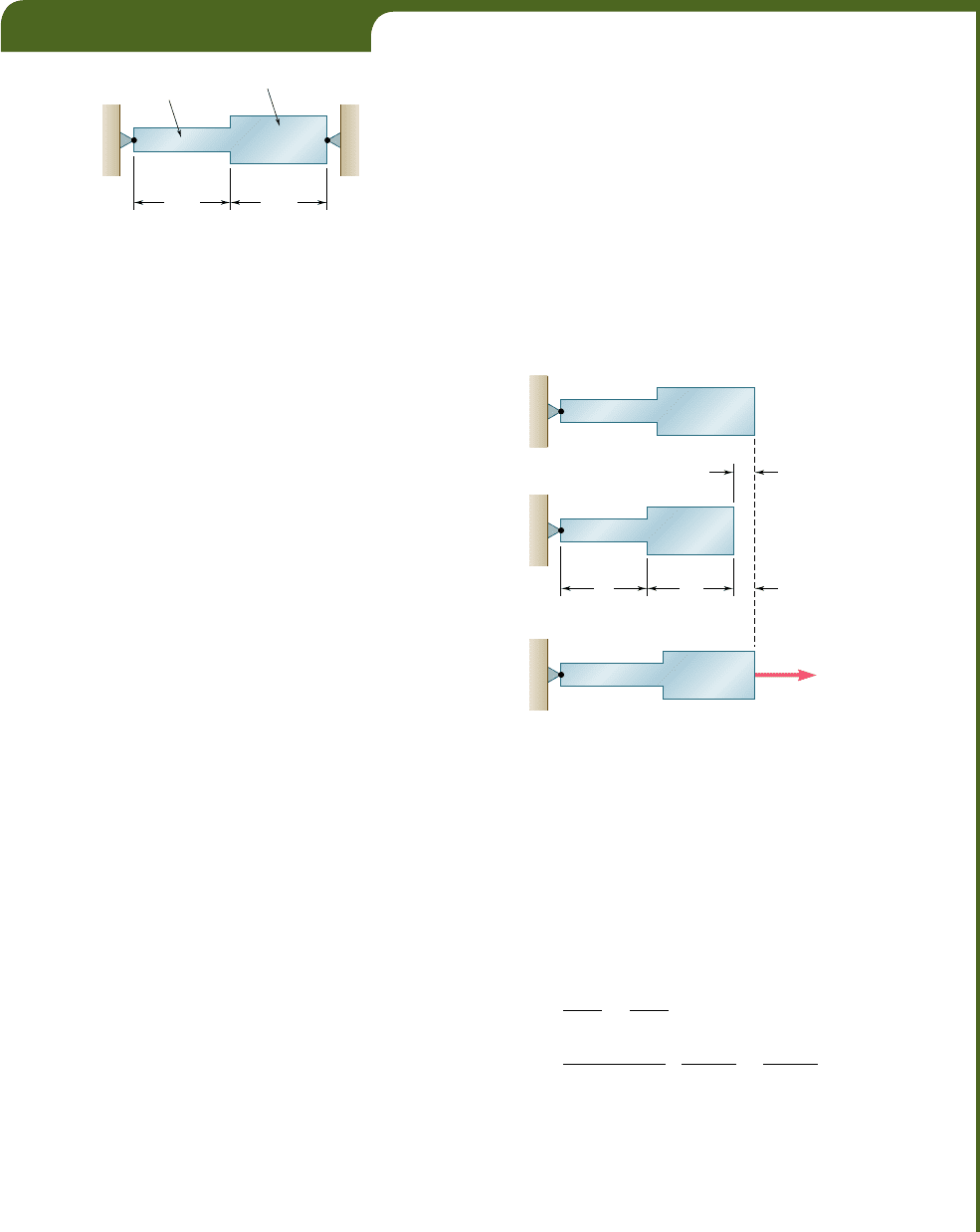
Let us first consider a homogeneous rod AB of uniform cross
section, which rests freely on a smooth horizontal surface (Fig.
2.30a). If the temperature of the rod is raised by DT, we observe
that the rod elongates by an amount d
T
which is proportional to both
the temperature change DT and the length L of the rod (Fig. 2.30b).
We have
d
T
5 a(DT)L (2.21)
where a is a constant characteristic of the material, called the coef-
ficient of thermal expansion. Since d
T
and L are both expressed in
units of length, a represents a quantity per degree C, or per degree
F, depending whether the temperature change is expressed in degrees
Celsius or in degrees Fahrenheit.
A
L
L
B
B
(b)
A
(a)
T
␦
Fig. 2.30 Elongation of rod due to
temperature increase.
With the deformation d
T
must be associated a strain P
T
5 d
T
yL.
Recalling Eq. (2.21), we conclude that
P
T
5 aDT (2.22)
The strain P
T
is referred to as a thermal strain, since it is caused by
the change in temperature of the rod. In the case we are considering
here, there is no stress associated with the strain P
T
.
Let us now assume that the same rod AB of length L is placed
between two fixed supports at a distance L from each other (Fig.
2.31a). Again, there is neither stress nor strain in this initial condi-
tion. If we raise the temperature by DT, the rod cannot elongate
because of the restraints imposed on its ends; the elongation d
T
of
the rod is thus zero. Since the rod is homogeneous and of uniform
cross section, the strain P
T
at any point is P
T
5 d
T
yL and, thus, also
zero. However, the supports will exert equal and opposite forces P
and P9 on the rod after the temperature has been raised, to keep it
bee80288_ch02_052-139.indd Page 82 9/4/10 5:17:00 PM user-f499bee80288_ch02_052-139.indd Page 82 9/4/10 5:17:00 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02
Apago PDF Enhancer
83
from elongating (Fig. 2.31b). It thus follows that a state of stress
(with no corresponding strain) is created in the rod.
As we prepare to determine the stress s created by the tem-
perature change DT, we observe that the problem we have to solve
is statically indeterminate. Therefore, we should first compute the
magnitude P of the reactions at the supports from the condition that
the elongation of the rod is zero. Using the superposition method
described in Sec. 2.9, we detach the rod from its support B (Fig.
2.32a) and let it elongate freely as it undergoes the temperature
change DT (Fig. 2.32b). According to formula (2.21), the correspond-
ing elongation is
d
T
5 a(DT)L
Applying now to end B the force P representing the redundant reac-
tion, and recalling formula (2.7), we obtain a second deformation
(Fig. 2.32c)
d
P
5
PL
AE
Expressing that the total deformation d must be zero, we have
d 5 d
T
1 d
P
5 a1¢T2L 1
PL
AE
5 0
from which we conclude that
P 5 2AEa(DT)
and that the stress in the rod due to the temperature change DT is
s 5
P
A
52Ea1¢T2
(2.23)
It should be kept in mind that the result we have obtained here
and our earlier remark regarding the absence of any strain in the rod
apply only in the case of a homogeneous rod of uniform cross section.
Any other problem involving a restrained structure undergoing a
change in temperature must be analyzed on its own merits. However,
the same general approach can be used, i.e., we can consider separately
the deformation due to the temperature change and the deformation
due to the redundant reaction and superpose the solutions obtained.
2.10 Problems Involving Temperature Changes
L
(b)
AB
AB
P'
P
(a)
Fig. 2.31 Rod with ends restrained
against thermal expansion.
L
(b)
(c)
L
A
AB
B
P
(a)
T
␦
AB
P
␦
Fig. 2.32 Superposition method
applied to rod restrained against
thermal expansion.
bee80288_ch02_052-139.indd Page 83 9/4/10 5:17:02 PM user-f499bee80288_ch02_052-139.indd Page 83 9/4/10 5:17:02 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02
Apago PDF Enhancer
EXAMPLE 2.06
Determine the values of the stress in portions AC and CB of the steel
bar shown (Fig. 2.33) when the temperature of the bar is 2508F, knowing
that a close fit exists at both of the rigid supports when the temperature
is 1758F. Use the values E 5 29 3 10
6
psi and a 5 6.5 3 10
6
/8F for
steel.
We first determine the reactions at the supports. Since the problem
is statically indeterminate, we detach the bar from its support at B and
let it undergo the temperature change
¢T 5 1250°F22 175°F252125°F
The corresponding deformation (Fig. 2.34b) is
d
T
5 a
1
¢T
2
L 5
1
6.5 3 10
2
6
/°F
21
2125°F
21
24 in.
2
5 219
.
50 3 10
2
3
in
.
C
A
A
⫽ 0.6 in
2
A
⫽ 1.2 in
2
12 in.12 in.
B
Fig. 2.33
(b)
(c)
R
B
(a)
T
␦
R
␦
C
A
B
C
L
1
L
2
A
B
C
12
12
A
B
Fig. 2.34
Applying now the unknown force R
B
at end B (Fig. 2.34c), we use Eq. (2.8)
to express the corresponding deformation d
R
. Substituting
L
1
5 L
2
5 12 in.
A
1
5 0.6 in
2
A
2
5 1.2 in
2
P
1
5 P
2
5 R
B
E 5 29 3 10
6
psi
into Eq. (2.8), we write
d
R
5
P
1
L
1
A
1
E
1
P
2
L
2
A
2
E
5
R
B
29 3 10
6
psi
a
12 in.
0.6 in
2
1
12 in.
1.2 in
2
b
5
1
1.0345 3 10
2
6
in./lb
2
R
B
Expressing that the total deformation of the bar must be zero as a result
of the imposed constraints, we write
d 5 d
T
1 d
R
5 0
5 219.50 3 10
2
3
in. 1
1
1.0345 3 10
2
6
in./lb
2
R
B
5 0
84
bee80288_ch02_052-139.indd Page 84 9/4/10 5:17:07 PM user-f499bee80288_ch02_052-139.indd Page 84 9/4/10 5:17:07 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02

Apago PDF Enhancer
from which we obtain
R
B
5 18.85 3 10
3
lb 5 18.85 kips
The reaction at A is equal and opposite.
Noting that the forces in the two portions of the bar are P
1
5 P
2
5
18.85 kips, we obtain the following values of the stress in portions AC
and CB of the bar:
s
1
5
P
1
A
1
5
18.85 kip
s
0.6 in
2
5131.42 ksi
s
2
5
P
2
A
2
5
18.85 kip
s
1.2 in
2
5115.71 ksi
We cannot emphasize too strongly the fact that, while the total
deformation of the bar must be zero, the deformations of the portions AC
and CB are not zero. A solution of the problem based on the assumption
that these deformations are zero would therefore be wrong. Neither can
the values of the strain in AC or CB be assumed equal to zero. To amplify
this point, let us determine the strain P
AC
in portion AC of the bar. The
strain P
AC
can be divided into two component parts; one is the thermal
strain P
T
produced in the unrestrained bar by the temperature change DT
(Fig. 2.34b). From Eq. (2.22) we write
P
T
5 a ¢T 5
1
6.5 3 10
2
6
/°F
21
2125°F
2
52812
.
5 3 10
2
6
in
./
in
.
The other component of P
AC
is associated with the stress s
1
due to the
force R
B
applied to the bar (Fig. 2.34c). From Hooke’s law, we express
this component of the strain as
s
1
E
5
131.42 3 10
3
psi
29 3 10
6
psi
511083.4 3 10
26
in./in.
Adding the two components of the strain in AC, we obtain
P
AC
5 P
T
1
s
1
E
52812.5 3 10
26
1 1083.4 3 10
26
5 12
71
3
10
26
i
n./
i
n.
A similar computation yields the strain in portion CB of the bar:
P
CB
5 P
T
1
s
2
E
52812.5 3 10
26
1 541.7 3 10
26
522
71
3
10
26
i
n./
i
n.
The deformations d
AC
and d
CB
of the two portions of the bar are
expressed respectively as
d
AC
5 P
AC
1
AC
2
5
1
1271 3 10
26
21
12 in.
2
5 1
3.
2
5
3
10
23
i
n.
d
CB
5 P
CB
1
CB
2
5
1
2271 3 10
26
21
12 in.
2
5 23
.
25 3 10
2
3
in
.
We thus check that, while the sum d 5 d
AC
1 d
CB
of the two deforma-
tions is zero, neither of the deformations is zero.
85
bee80288_ch02_052-139.indd Page 85 11/1/10 11:30:03 PM user-f499bee80288_ch02_052-139.indd Page 85 11/1/10 11:30:03 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02
Apago PDF Enhancer
86
SAMPLE PROBLEM 2.3
The
1
2
-in.-diameter rod CE and the
3
4
-in.-diameter rod DF are attached to
the rigid bar ABCD as shown. Knowing that the rods are made of aluminum
and using E 5 10.6 3 10
6
psi, determine (a) the force in each rod caused
by the loading shown, (b) the corresponding deflection of point A.
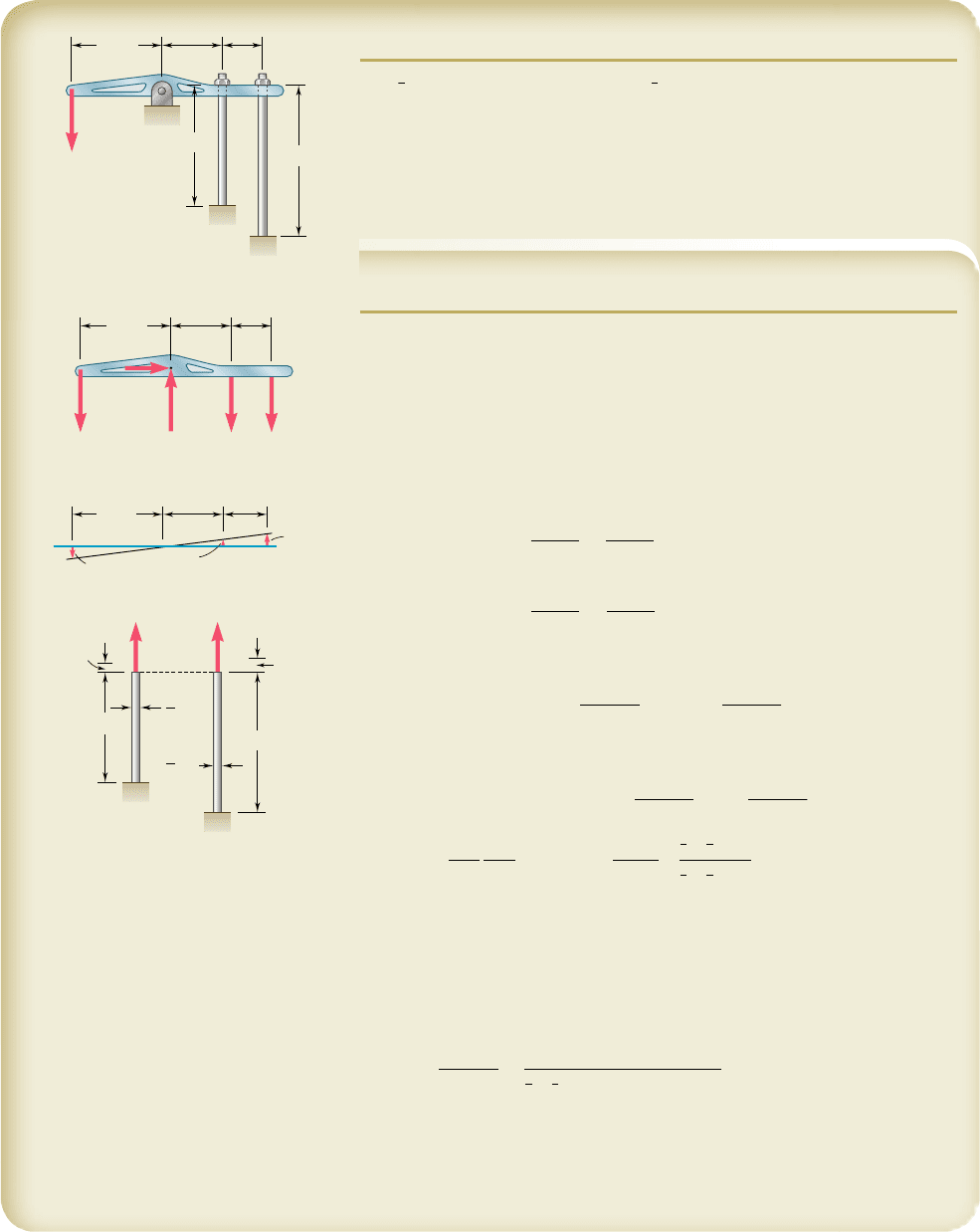
SOLUTION
Statics. Considering the free body of bar ABCD, we note that the
reaction at B and the forces exerted by the rods are indeterminate. However,
using statics, we may write
1
l
o M
B
5 0: 110 kips2118 in.22 F
CE
112 in.22 F
DF
120 in.25 0
12
F
C
E
1
20
F
DF
5
180
(1)
Geometry. After application of the 10-kip load, the position of the bar
is A9BC9D9. From the similar triangles BAA9, BCC9, and BDD9 we have
d
C
1
2 i
n.
5
d
D
2
0
i
n.
d
C
5 0.6d
D
(2)
d
A
18
i
n.
5
d
D
2
0
i
n.
d
A
5 0.9d
D
(3)
Deformations. Using Eq. (2.7), we have
d
C
5
F
CE
L
CE
A
C
E
E
d
D
5
F
DF
L
DF
A
DF
E
Substituting for d
C
and d
D
into (2), we write
d
C
5 0.6d
D
F
CE
L
CE
A
C
E
E
5 0.6
F
DF
L
DF
A
DF
E
F
CE
5 0.6
L
DF
L
CE
A
CE
A
DF
F
DF
5 0.6 a
30 in.
24 in.
bc
1
4
p1
1
2
in.2
2
1
4
p
1
3
4
in.
2
2
d F
DF
F
CE
5 0.333F
DF
Force in Each Rod. Substituting for F
CE
into (1) and recalling that all
forces have been expressed in kips, we have
12
1
0.333F
DF
2
1 20F
DF
5 180 F
DF
5 7.50
k
ips
◀
F
CE
5 0.333F
DF
5 0.33317.50 kips2 F
CE
5 2.50 kips
◀
Deflections. The deflection of point D is
d
D
5
F
DF
L
DF
A
DF
E
5
17.50 3 10
3
lb2 130 in.2
1
4
p1
3
4
in.2
2
110.6 3 10
6
psi2
d
D
5 48.0 3 10
23
in.
Using (3), we write
d
A
5 0.9d
D
5 0.9
1
48.0 3 10
2
3
in.
2
d
A
5 43.2 3 10
2
3
in.
◀
30 in.
24 in.
C
D
CD
E
F
in.
1
2
in.
3
4
F
CE
F
DF
18 in.
12 in. 8 in.
F
CE
B
y
B
x
F
DF
10 kips
B
C
D
A
18 in.
12 in.
30 in.
24 in.
8 in.
10 kips
B
E
F
C
D
A
18 in.
12 in. 8 in.
B
C'
D'
CD
A
A'
A
C
D
bee80288_ch02_052-139.indd Page 86 11/1/10 11:30:05 PM user-f499bee80288_ch02_052-139.indd Page 86 11/1/10 11:30:05 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch02
