Bear H.S. Understanding Calculus

Подождите немного. Документ загружается.

Chapter 12 • The Definite Integral

12.10

o 1+x

12.11

.JI=X2

o 1 - x

12.

o 1+x

Graphthe regionand findthe area boundedby the following curves.

12.13 The x-axis and the curve

y =9 - x

•

12.14 The x-axis and the one archof the curve y = sinx (e.g.,0

z ),

12.15 The curves y =4 - x

and y =x + 2.

12.16 The curves y = 1 - x

and y =x

- 1.

12.17 The y-axis and the curvex =2y - y2.

12.18 The y-axis, the curve x = y3, and the line y = 1.

12.19 The curves y = sinx and y =

for 0

12.20 The coordinate axes,the curve y = 2x

+4x + 3, and the line x = 1.

12.21 Showthat

f(u)

du =

f(x).

Hint: Let F'(x) =

f(x)

fax

f(u)

du =

F(x)-F(a).

12.22 Use Problem

12.21

to calculatethe

following.

d 1

(i) - e

t 2

dx 0

d l

(ii) -

~du

dx 1

(iii)

sin

02dO

dx 1C

(iv)

1°

log(l

S2)

12.23 Use Problem

12.21

and the chain rule to evaluate

f:(X)

f(u)

duo

Hint: Let F(x) =

fax

f(u)

du, so the problemis to evaluate

F(g(x».

Work,

Volume,

Force

In this chapter we consider some other applications of the definite integral. First, we examine

the work done by a force acting over a given

distance-for

example, the work done pushing a

car up a slope or lifting a bucket

water. For a constant force F acting in the direction of the

motion, work is simply force times distance:

W=F·d.

If the force is not constant (the car is pushed up a slope of increasing steepness, or the bucket

is leaking water as it's lifted), then we are led to a definite integral.

Suppose the force applied at a point x is given by the nonconstant function

f(x).

divide up the interval [a,

b] over which the force acts into small subintervals

[Xi

-I,

xil

which the force is nearly constant. If

c, E [Xi-I,

xil,

then

f(x)

will differ little from f(Ci) for

Xi-I:::: X

::::

Xi,

and the work done from Xi-I to Xi is approximately

fic,

)(Xi - Xi-I). The total

work done from

a to b is approximately

E7=1

f(Ci )(Xi - Xi-I). As the lengths of the integrals

get smaller, so maxtx, - Xi-I)

-----+

0, these better and better approximations approach the

definite integral as a limit, and that is the work done by

f(x)

from a to b:

= l

f(x)dx.

When setting up such a work problem we can skip the intermediate step of approximating

the work over many small intervals. Think of the increment

work done by the force f (x)

over the interval

length

as f (x)

dx,

and the total work as the sum (integral)

all these

increments.

EXAMPLE

13.1

The force F required to stretch a steel spring is proportional to the distance the spring is stretched, so

F = kx where k is a constant. Suppose a two-pound force stretches a spring 4 inches. How much work

is done in stretching the spring from 4 inches to 12 inches?

Solution

First, we determine the constant k, and since work is generally measured in foot pounds we measure

distance in feet. We are given that

2lbs

corresponds to 4 in

£1),

so 2 =

~k,

and k = 6Ibs/ft. Therefore,

UnderstandingCalculus

F(x) =6x. The work done in stretchingfrom tfoot to I foot is

i 2

1 8

W = 6x dx =3x I =3 - - = - ft-Ibs.

! 3 3 3

EXAMPLE

13.2

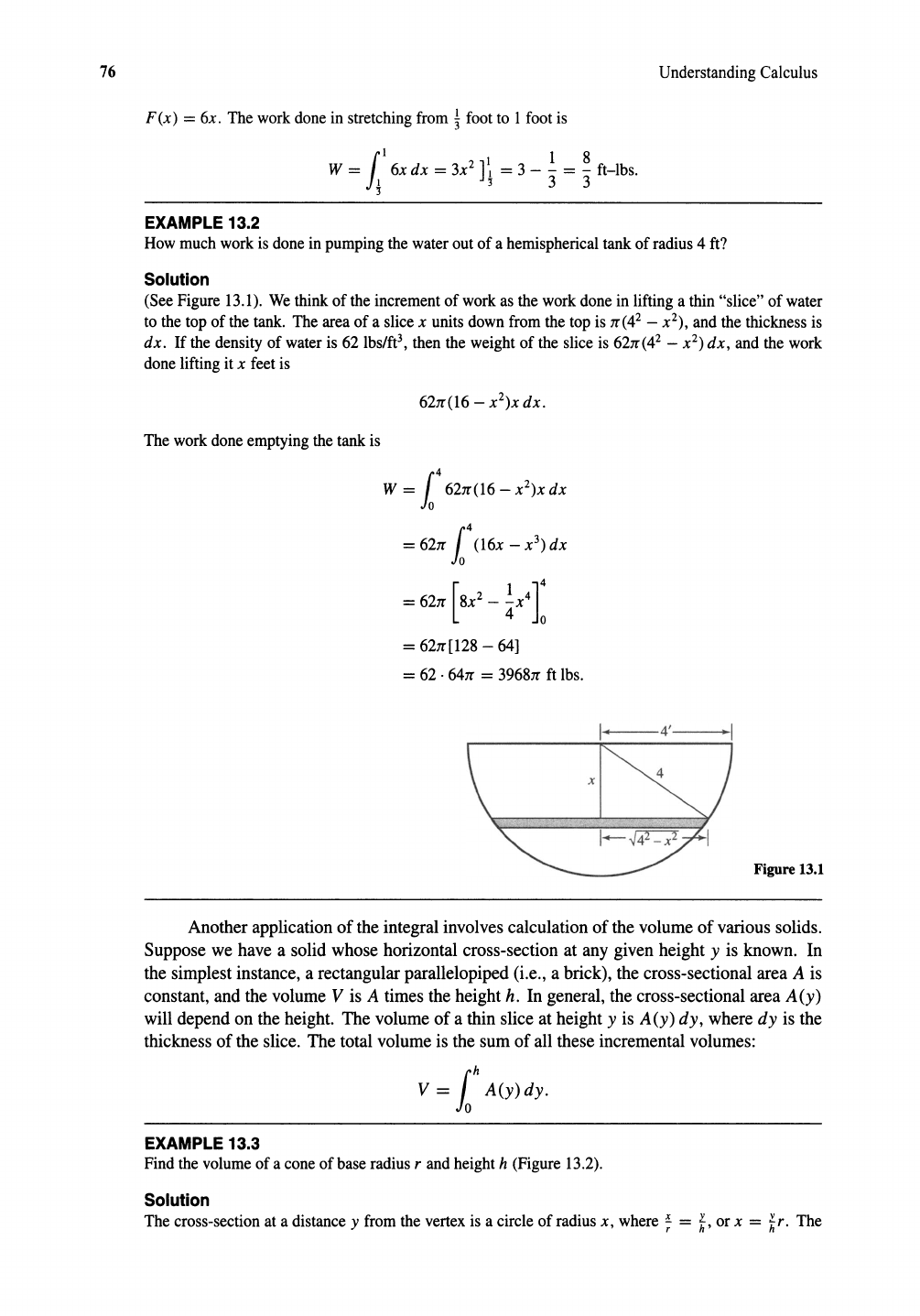
How much work is done in pumping the waterout of a hemisphericaltank of radius 4 ft?

Solution

(See Figure 13.1). Wethink of the increment of work as the work done in lifting a thin "slice" of water

to the top of the tank. The area of a slice

x units down from the top is

1T(4

) ,

and the thickness is

dx. If the density of water is 62 lbs/ft", then the weight of the slice is

621T(4

- x

) dx, and the work

done lifting it

x feet is

The work done emptyingthe tank is

W =1

621T(l6

- x

2)x

621T

(16x - x

) dx

621T

[8x

~X4

621T[128

- 64]

=62 .

641T

39681T

ft Ibs.

Figure 13.1

Another application of the integral involves calculation of the volume of various solids.

Suppose we have a solid whose horizontal cross-section at any given height y is known. In

the simplest instance, a rectangular parallelopiped (i.e., a brick), the cross-sectional area A is

constant, and the volume V is A times the height h. In general, the cross-sectional area

A(y)

will depend on the height. The volume of a thin slice at height y is

A(y)

dy,

where dy is the

thickness of the slice. The total volume is the sum of all these incremental volumes:

V = l

A(y)dy.

EXAMPLE

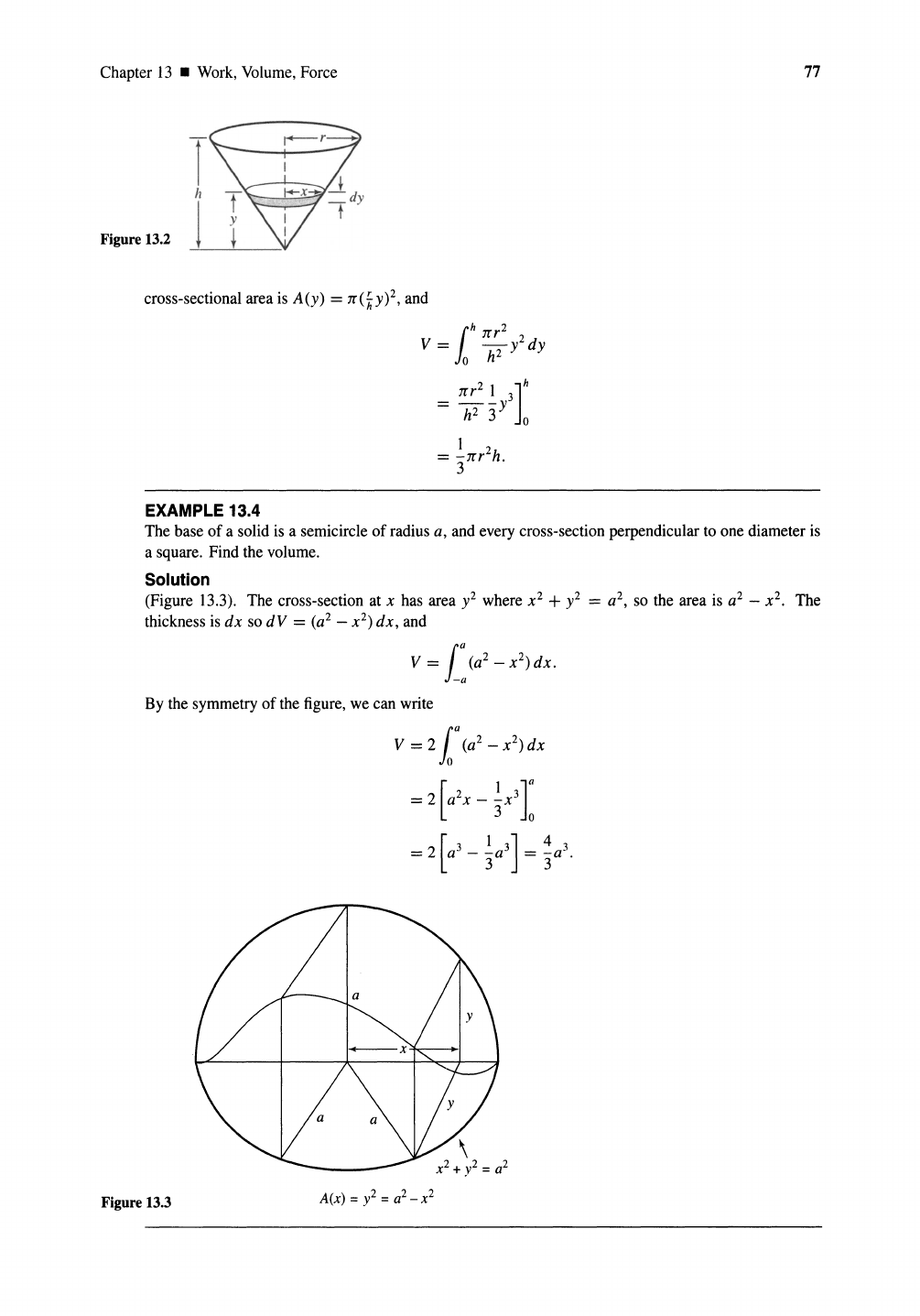
13.3

Find the volumeof a cone of base radius r and height h (Figure 13.2).

Solution

The cross-sectionat a distance y from the vertex is a circle of radius x, where

or x = *r, The

Chapter 13 • Work, Volume, Force

Figure 13.2

cross-sectional area is A( y) =

Jr(~y)

and

nr?

V =

l dy

_ Jrr

3]h

- h

I 2

"3Jrr

EXAMPLE

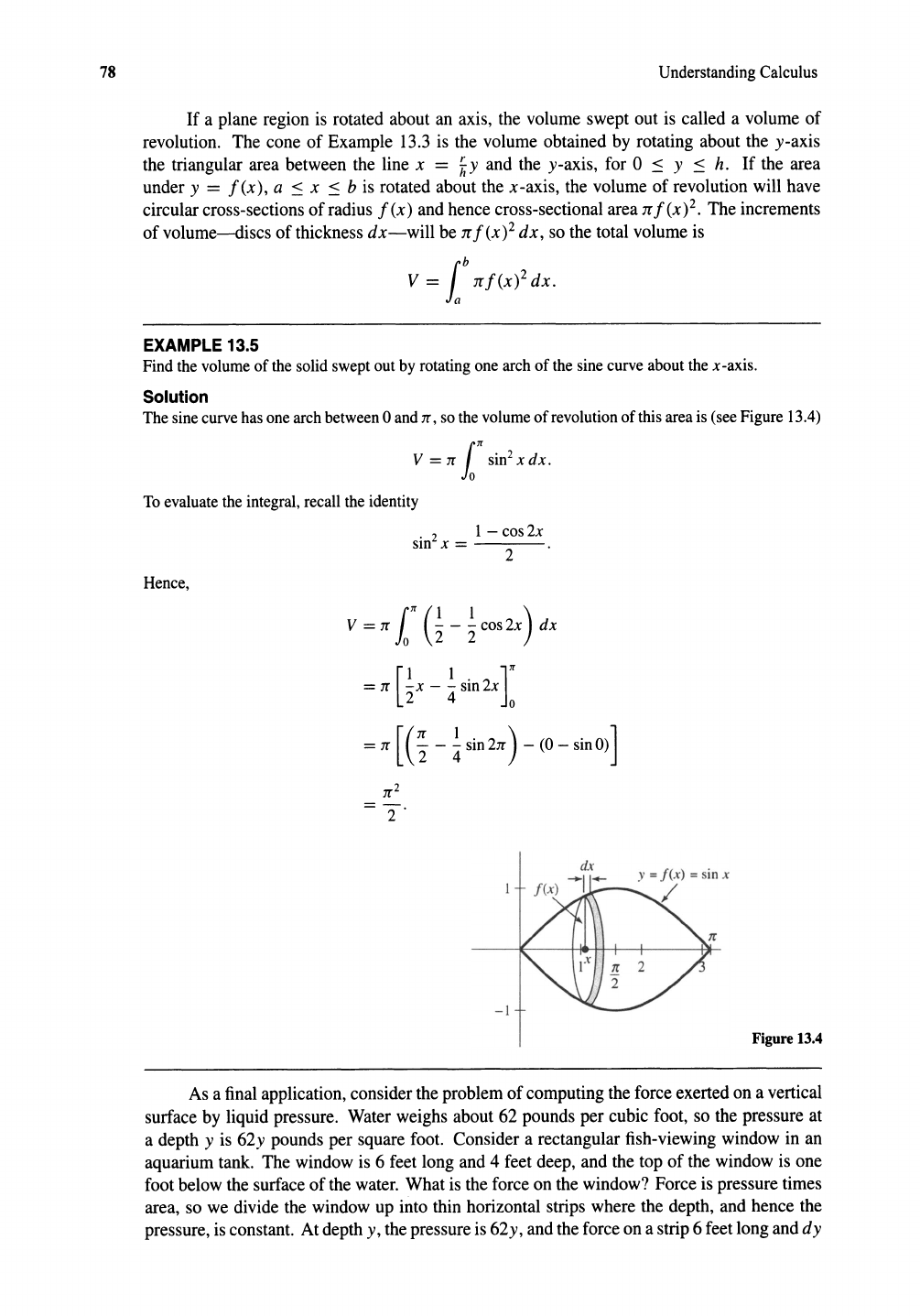
13.4

The base of a solid is a semicircle of radius a, and every cross-section perpendicular to one diameter is

a square . Find the volume.

Solution

(Figure 13.3). The cross-section at x has area y2 where x

+ y2 = a

, so the area is

. The

thickness is

dx so

=(a

- x

) dx, and

V =

- x

2)dx

By the symmetry of the figure, we can write

V =

- x

) dx

Figure 13.3

Understanding Calculus

a plane region is rotated about an axis, the volume swept out is called a volume of

revolution. The cone of Example 13.3 is the volume obtained by rotating about the y-axis

the triangular area between the line x =

y and the y-axis, for 0 S y S h. If the area

under y =

x ), a S x S b is rotated about the x-axis, the volume of revolution will have

circular cross-sections ofradius f (

and hence cross-sectional area

f (x)2 . The increments

of volume

-d

iscs of thickness

dx-will

be n f (x )2

, so the total volume is

V =I

rrf(x

EXAMPLE

13.5

Find the volumeof the solid sweptout by rotatingone arch of the sine curve about the x-axis.

Solution

The sine curvehasone arch between0 and

71'.

so the volumeof revolution of thisarea is (see Figure 13.4)

V =

71'

sirr' x dx .

Toevaluatethe integral.recall the identity

. 2

cos2x

ill

x = 2 .

Hence,

[

I I

71'

- X - - sin 2x

71'

[

sin

271'

) - (0 - sin0)]

- I

Figure 13.4

As a final application, consider the problem of computing the force exerted on a vertical

surface by liquid pressure. Water weighs about 62 pounds per cubic foot, so the pressure at

a depth y is 62y pounds per square foot. Consider a rectangular fish-viewing window in an

aquarium tank. The window is 6 feet long and 4 feet deep, and the top of the window is one

foot below the surface of the water. What is the force on the window? Force is pressure times

area, so we divide the window up into thin horizontal strips where the depth, and hence the

pressure, is constant. At depth y, the pressure is 62y, and the force on a strip 6 feet long and

Chapter 13 • Work, Volume, Force

high is

= (62y)(6dy). The total force on the window, with y ranging from 1 to 5 feet, is

F =i

(62)(6)y dy

62·

2 1

= 62 . 3 . (25 - 1) = 4464 lbs.

PROBLEMS

13.1 Find the work done in stretching a spring 2 feet, if a force of 3 pounds is required to stretch

the spring 6 inches.

13.2 A 20-pound weight is hung from a spring, and the spring stretches 8 inches. How much

work is done in pulling the weight down an additional foot?

13.3 A leaking bucket of water is lifted 50 feet. The bucket weighs 60 pounds initially and loses

weight uniformly until it weighs 30 pounds at the top. How much work was done?

13.4 How much work is done in pumping the water out the top of a cylindrical tank whose

radius is 4 feet and whose depth is 6 feet?

Hint: Consider the increment of work done in

lifting a "slice" of water

y feet from the top and

dythick.

The slice weighs 62 . n . 4

2dy,

and the work done lifting this slice up y units is its weight times y.

13.5 Find the work done in pumping the top 2 feet of water out of a hemispherical bowI of

radius 5 feet.

Hint: The slice at depth y feet has radius x = J52 - y2.

13.6 An irregular solid has horizontal cross-sectional area at height y equal to A(y) =

for 0 s y

9. What is its volume?

13.7 In Example 13.4 suppose the solid again has a base that is a semicircle of radius

a, but

now the vertical cross-sections are quarter circles. Find the volume.

13.8 Find the volume of the sphere obtained by rotating about the x-axis the area under the

curve

y = ,Ja

-a

13.9 What is the volume obtained by rotating the area under the parabola y =x

for 0

about the x-axis?

13.10 Rotate the area of Problem 13.9 about the y-axis. What is the volume?

Hint: The slices

for fixed

y are washers with thickness dy, outer radius 1, inner radius

.JY.

13.11 Rotate about the y-axis the area between the curve y =

sin-

x and the y-axis, for 0

::s

I· What is the volume?

13.12 Find the volume of the ellipsoid obtained by rotating the ellipse

= 1 about the

x-axis. Then find the volume of rotation about the y-axis.

13.13 A body moving with constant velocity

v goes a distance

V(t2

- t) .between times 1) and

12.

If v

(t)

is a varying velocity, the distance is

/,:2

(t)

d1. Show that if a body has constant

acceleration

a, so v = at, then the distance it travels in 1 seconds is

~at2.

(If a is the

acceleration of gravity, 32

ft/sec",

then this is the falling body again.)

...

13.14 Suppose a car has a constant acceleration and goes from 0 to 60 mph in 6 seconds. How far

does the car go in these 6 seconds?

Hint: 60 mph is 88 ft/sec, so v =

ft/sec at time t.

13.15 The shallow end of a swimming pool is a vertical rectangle, 4 feet deep and 20 feet across.

What is the force on this surface exerted by the water when the pool is full?

13.16 A 15-foot chain weighing 2 lbs/ft lies coiled on the ground. A line of negligible weight

is attached to one end and used to lift the chain straight up until the bottom just clears the

ground. How much work was done?

13.17 A 10-foot chain weighing

kIb per foot hangs from a roof. How much work is done in

pulling the chain up onto the roof?

Parametric

Equations

So far we have described curves with equations of the form Y =

f(x)

or F(x, y) =

describe the path of a moving object, it is frequently more convenient and more relevant to

determine the individual coordinates as functions of time

thus,

x =

g(t),

y =

f(t).

(14.1)

Equations (14.1) are called

parametric equations of a curve, and the variable t is called the

parameter.

EXAMPLE 14.1

A cannon fires a projectile with muzzle velocity v at an elevation () from the horizontal. Describe the

path of the projectile.

Solution

(See Figure 14.1.) The horizontal component of the velocity is v cos f), and that is the constant speed in

the

x-direction. Therefore, with the cannon at the origin,

x = (v cos

())t.

The initial vertical component of the velocity is v sin (), so as we have seen earlier, the motion in the

vertical direction is given by

y = (v sin ())t - 16t

where the term

-16t

is due to the downward acceleration of gravity. The two equations

x = (v cos

())t

y =

(vsin())t

-16t

are parametric equations of the path of the projectile.

(14.2)

The Cartesian equation that corresponds to a given pair of parametric equations can be

found by eliminating the parameter to get an equation in x and y. For example, in (14.2) we

could solve the first equation for

t and substitute that expression in the second equation. This

Understanding Calculus

gives

v sin f)

v cos f)

Figure 14.1

(14.3)

(14.4)

t =x / v cos 0,

y = (v sinO)

(_X_)

_16

(_x_·

_)2

v cos 0 v cos 0

16 2

= (tan O)x - v

cos

0 X •

Since y is a quadratic function

x (remember that 0 and v are given constants), the path is a

parabola.

In Example 14.1, the parameter is time, which is most appropriate when the curve is the

path

a moving object. Curves can also be described in terms

a parameter that has purely

geometric significance. A simple illustration is the curve

x = cosO

y = sin 0

for 0

::::

n . If the parameter were unrestricted, then equations (14.3) would be the

parametric equations

the unit circle, and the parameter 0 would be the distance you would

have to go around the circle from

(1, 0) to get to

(x,

y). Since in (14.3) () is restricted to [0, 1f],

(14.3)

represents

just

the top half of the unit circle.

A parametrically defined curve may consist

only a part

the corresponding Cartesian

curve that results when the parameter is eliminated. Consider the curve

x = sin 0, y = 1 - sin

The corresponding Cartesian equation is

y = 1 - x

•

(14.5)

Notice, however, that in equation

(14.4) x takes only values between

-1

and 1, and y takes

only values between

0 and 1. The parametric curve (14.5) therefore consists only

the part

the parabola (14.5) for

-1

::::

To find the slope of a parametric curve x =

x(t),

Y = yet), let

and 6.y be the

corresponding changes in

x and y, both

which result from a change 6.t in t, Then

dy .

hm-

LH~O

6.x

= lim 6.y / 6.t

~t~O

/sx]

jdx.

dt dt

For example, the slope

the parabola (14.4) at the point corresponding to a given 0 is

(14.6)

-2

sin 0 cos 0

-'------

-2

sin

cosO

Chapter 14 • Parametric Equations

When

I' so the point is (1, 0),

-2

sin

-2.

Whenx and

yare

givenin termsof a parametert, then the calculationof the slopegives

as a functionof t. To find

~:~

we simply use (14.6) again to findthe derivative of

with

respect to

x in this situationwhere both x and

are functions of t. That is

---.1::

= di

d~x

(14.7)

dx? dt

EXAMPLE 14.2

Find the tangent line to y = t

+ 1, x = 3t - 2 at t = 1, and tell whether the curve lies over or under the

tangent line near

(x(l),

y(l)).

Solution

First calculate

dx =

= 3·

At t = 1, x = 1, y = 2, and *=

Hence, the tangent line at (1, 2) has the equation

y-2=3(x-l).

Recall that if

~:~

is positive, the first derivative is increasing, and the curve is concave up. A

curve that is concave up will lie above its tangent lines, and a curve that is concave down

< 0) will

lie below its tangent lines. We use (14.7) to calculate

--2 _ di

dx? - dx

f,(¥) _ 2,

3 9

The curve has a constant positive second derivative and so is concave up everywhere, and the curve lies

over every tangent line. To change to Cartesian coordinates, solve for

t, t =

(x + 2), and substitute in

the formula for

Y=[~(X+2)r+l

1 2

g(x

+ 2) + 1.

The curve is an upward-pointing parabola.

Let

f(t)

and get) be any two differentiable functions on an interval [a, b], and consider

the curve

x = get), y =

f(t),

Supposethat g/

(t)

> 0 on [a, b] so thatx increasesand the curvemovesfrom left to right as t

goesfroma tob. BytheordinaryMean

Value

Theorem,theremustbesomepoint(g(to), f(to»

on the curve between (g(a),

f(a»

and (g(b),

feb»~

where the slope of the curve is the same

as the slope of the secant line;

namely,

(f(b)

f(a»/(g(b)

g(a».

Since the slope of the

curve is givenby

f'(t)

g/(t) ,

UnderstandingCalculus

this says that there must be some to in (a, b) such that

f(b)

f(a)

f'(to)

(14.8)

g(b) - g(a) g'(to)

The statement above is called Cauchy's Mean Value Theorem. The two forms of the Mean

Value Theorem look different, since Cauchy's version (14.8) involves two functions, but the

geometric content is identical. A curve cannot get smoothly from P to

Q without somewhere

pointing in the same direction as the line segment joining P and Q.

The length of a curve is defined to be the limit of the lengths of polygonal paths joining

consecutive points along the curve. If the curve is given by parametric equations x =

x(t),

y =

y(t)

for a

::s

b, then for each partition a = to < tl < ti <

...

< t

= b of [a, b], we

get a polygonal path whose length is

I:Jtu;+/:}.y;.

i=1

where Sx, = X(ti+l)

-X(ti)

and dYi =

y(ti+l)

y(ti).

We can write the length of the polygon

n n (

(

2 2 Sx,

~Yi

I:J/:}.X

+/:}.Yj

/:}.t. +

/:}.t.

/:}.tj.

i=1

I I

(14.9)

As the partition becomes finer and finer, with max

~ti

0, the sums in (14.9) approach the

following integral, which is the arc length:

s = l

(~~r

(~r

dt.

(14.10)

If the curve is given in the form y = /

(x)

for a

::s

b, this is the same as the parametric

form

x = 1, Y =

/(1),

a::S 1

::s

and the integral (14.10) becomes

s =l

(~y

)1 +

(f'(x»2

dx.

EXAMPLE

14.3

Find the lengthof the curve x = 2t, y =

~t3/2,

Solution

· dx 2 d

2 1

mce dt = an dt = t i ,

s = 1

.J4+4tdt

= 2 {

.Jf+tdt

4 3 1 4 3

= - (1 + t)

] = -

(2"2

- 1).

(14.11)