Байгунусов В.Б. Судоводителям о плавучести и остойчивости судна
Подождите немного. Документ загружается.

38
Тогда, момент инерции прямоугольника относительно оси x определяется по про-
стой и компактной формуле
LB³
I
x = (13)
12
Допустим, что подводный объем судна V и координаты z
c и zg не изменяются. Тогда,
на основании формулы (10), можно утверждать, что с увеличением метацентриче-
ского радиуса (r) остойчивость (h) увеличивается. Используя формулы (12) и (13),
можно записать
LB³
r =
12V
Вообразим себе, что судно эластично и позволяет изменять размеры ватерлинии в
продольном и поперечном направлениях. При увеличении длины ватерлинии L ме-
тацентрический радиус увеличивается в первой степени (пропорционально), таким
же образом увеличивается и остойчивость. При увеличении ширины ватерлинии B
метацентрический радиус и, соответственно, остойчивость возрастают в кубе, т.е.
при расширении ватерлинии в 2 раза метацентрический радиус возрастет в 8 раз, в 3
раза – в 27 раз, в 4 раза – в 64 раза. Соответственно этому, будет возрастать (или
уменьшаться) остойчивость. Таким образом, остойчивость судна, в значительной
степени, зависит от ориентации размеров ватерлинии относительно продоль-
ной оси x.
Для закрепления понимания изложенного, рассмотрим следующий пример. Для
удержания судна, находящегося в аварийном (по остойчивости) состоянии, подвели
два понтона, которые можно пришвартовать двумя способами – к носу и к корме и
по бортам. Швартовка понтонов к оконечностям равнозначна увеличению длины
ватерлинии L, при этом остойчивость возрастет, но возрастет не намного. При швар-
товке к бортам (равнозначно увеличению B) остойчивость возрастет несопоставимо
намного.
Формулу (13) можно переписать следующим образом:
L*B*B² S*B²
Ix = , где L*B = S – площадь ватерлинии.То есть Ix = .
12 12
Отсюда видно, что момент инерции площади ватерлинии, метацентрический радиус
и, следовательно, остойчивость пропорциональны площади ватерлинии S и квадра-
ту ширины судна, т.е. с увеличением площади ватерлинии (при прочих равных усло-
виях) остойчивость увеличивается. Старорусское слово “остойчивость” в современ-
ном языке приобрело смысл “устойчивость”. Устойчивость какого-либо объекта
зависит от площади его опоры. Проводя параллель, можно утверждать, что площадь
ватерлинии является своеобразной площадью опоры судна.
Теперь предположим, что в формуле (12) момент инерции не изменяется, а изме-
няется подводный объем судна V. Тогда с увеличением подводного объема или
осадки судна остойчивость (при прочих равных условиях) уменьшается. Отсюда сле-
дует, что суда широкие с малой осадкой (например, речные) имеют во много раз
большую остойчивость, чем суда узкие с большой осадкой (боевые корабли).
51
крена, поэтому ЦТ жидкости переместится из точки g в точку g
1 (по пунктирной
стрелке). Несложно доказать, что при малых наклонениях траектория ЦТ жидкости
gg
1 представляет дугу окружности. При параллельном переносе веса жидкости рж из
точки g в g
1 возникает пара сил, создающая дополнительный кренящий момент
ΔМ
кр, уменьшающий восстанавливающий момент Мв. Таким образом, переливание
жидкости приводит к уменьшению остойчивости судна.
В описанном процессе наблюдается полная аналогия поведения жидкости со
свободной поверхностью с поведением подвешенного и перекатывающегося
грузов.
Эта аналогия логически приводит к тому, что с позиций теории остойчивости сле-
дует считать, что ЦТ жидкости находится в точке О – центре дуги gg
1, по которой
смещается центр тяжести жидкости. Иначе говоря, переливание жидкости равно-
значно ее вертикальному перемещению снизу вверх в точку О.
Изменение остойчивости при переливании жидкости оценивается по формуле (до-
казательство можно найти в любом учебнике по статике судна)
γ
ж* ix
Δh = ▬ ------ (19)
D
где γ
ж - удельный вес жидкости;
i
x – момент инерции свободной поверхности жидкости относительно оси x.
Из формулы (19) следует, что изменение остойчивости зависит только от момента
инерции i
x площади свободной поверхности, поскольку γж и D – величины постоян-
ные: с увеличением момента инерции увеличивается приращение остойчивости, но с
отрицательным знаком, т.е. остойчивость уменьшается.
x
б
)
а
)
b
b
ℓ
ℓ
ℓ
в
)
b/2
b/2
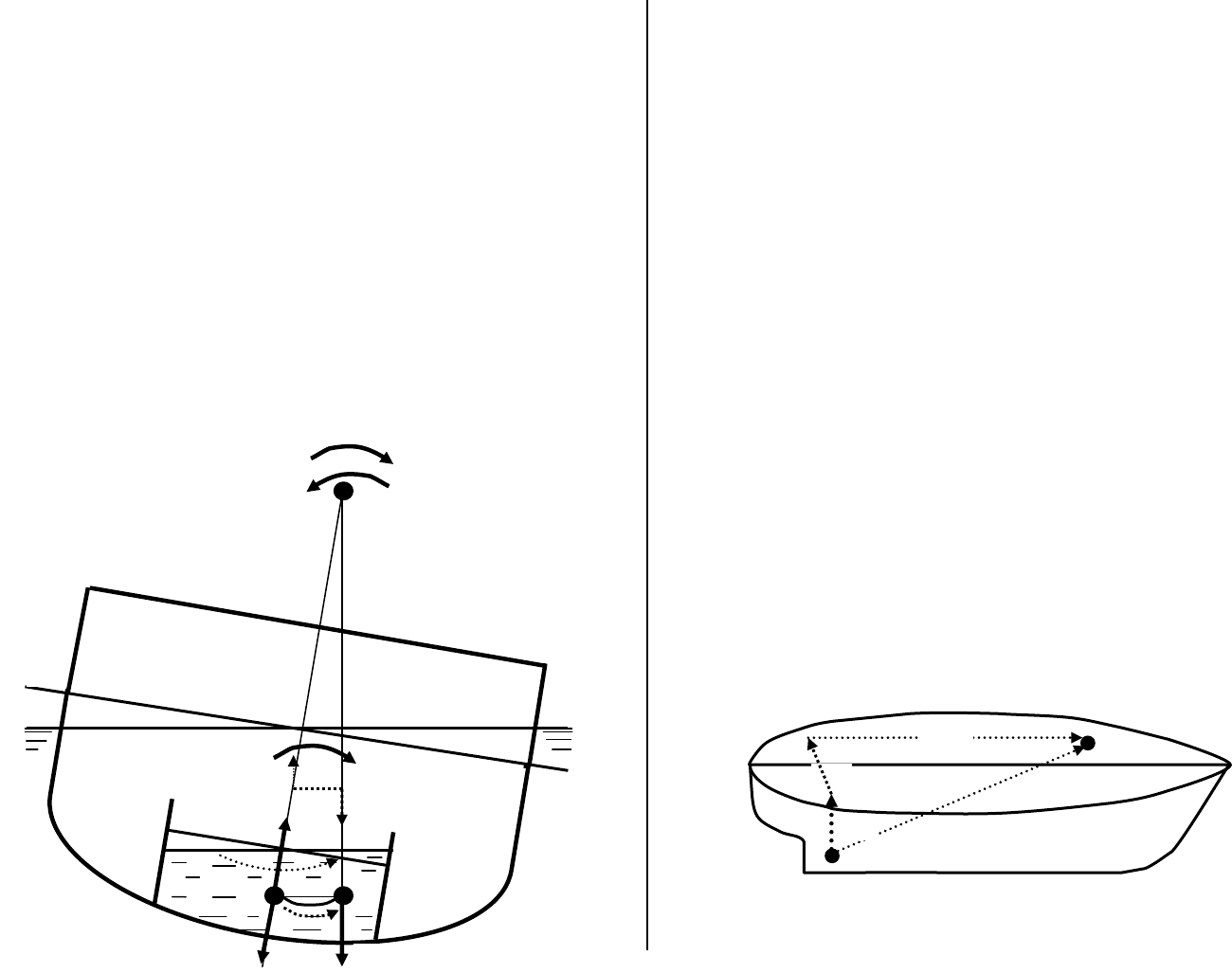
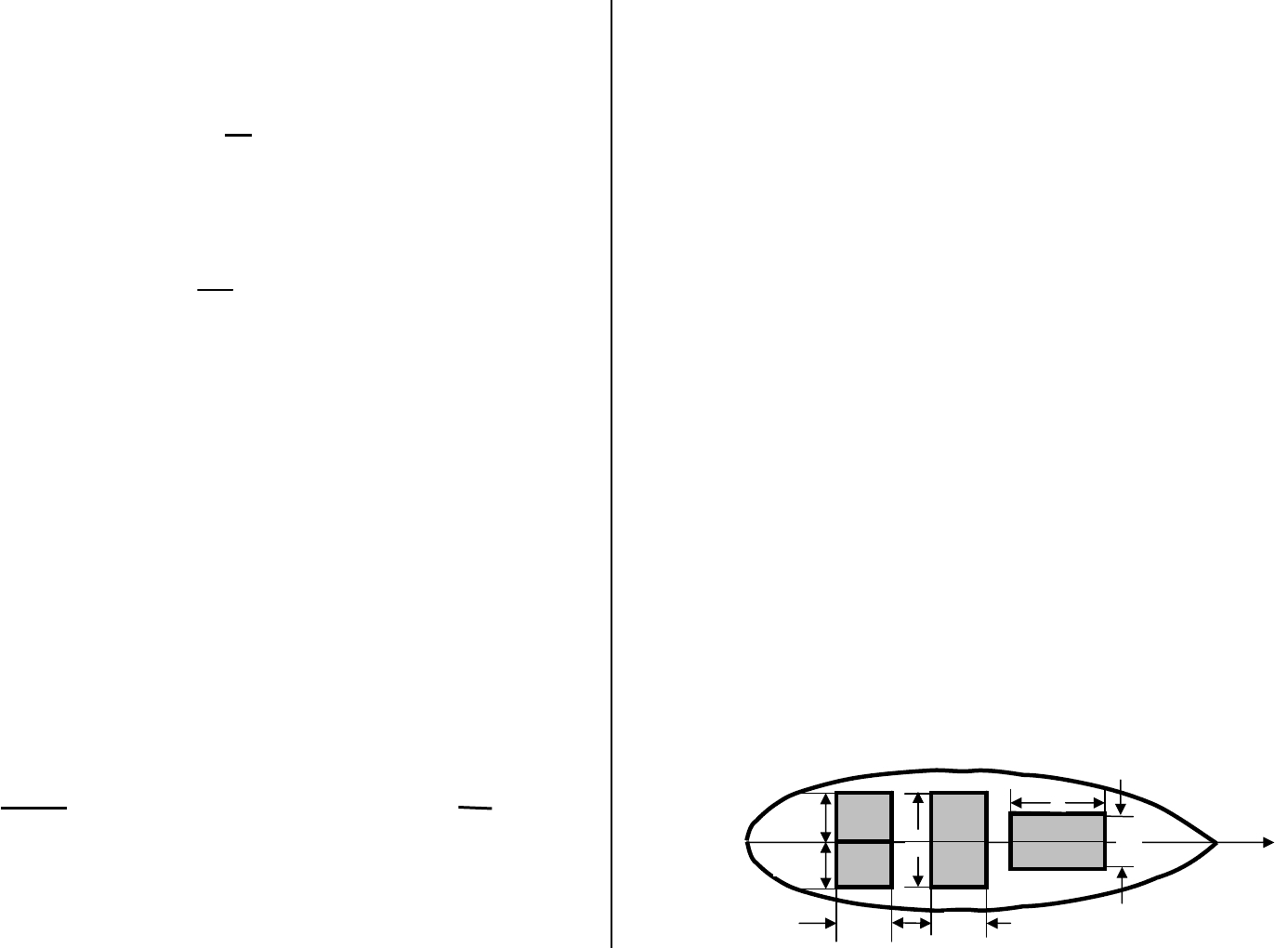
Рис. 4.1.6.2. Схема размеров и ориентации свободной поверхности в плане
Момент инерции площади (ватерлинии) рассматривался ранее в разделе 4.1.1., где
показано, что для прямоугольника (см. рис. 4.1.6.2.) момент инерции площади отно-
сительно оси x вычисляется по формуле
ℓ * b³
i
x = --------
(20)
12
Рассмотрим, как изменяется остойчивость с изменением размеров свободной по-
верхности.
50
4.1.6. ВЛИЯНИЕ СВОБОДНОЙ ПОВЕРХНОСТИ ЖИДКОГО ГРУЗА НА ОСТОЙЧИВОСТЬ
Аналогия с подвешенным и перекатывающимся грузом прослеживается и в
поведении другого подвижного груза - жидкого груза со свободной поверхно-
стью, который имеет возможность переливаться в сторону наклоненного борта.
Если жидкость заполняет цистерну полностью и не имеет свободной поверхно-
сти,то такой жидкий груз теоретически ничем не отличается от твердого груза.
Рис. 4.1.6.1. Схема, иллюстрирующая поведение жидкого груза со свободной по-
верхностью.
Сначала рассмотрим случай, когда жидкость “принадлежит” судну, т.е. у жидкого
груза первоначально свободной поверхности не было, затем по какой-то причине она
появилась. Судно эту жидкость не приняло и его водоизмещение D после образова-
ния свободной поверхности не изменилось. Жидкость находится в цистерне (см. рис.
4.1.6.1.) и ее уровень всегда параллелен ватерлинии. В прямом положении судна
(ватерлиния 0-0) ЦТ жидкости будет находится в точке g.
Приложив к судну кренящий момент М
кр, накреним его до ватерлинии 1-1, парал-
лельно которой установится уровень свободной поверхности. В результате, произой-
дет перетекание жидкости из клиновидного объема 1 в клиновидный объем 2 (пока-
зано пунктирной стрелкой), полнота объема цистерны сместится в сторону
39
4.1.2. ВЛИЯНИЕ ПЕРЕМЕЩЕНИЯ ГРУЗА НА ПОСАДКУ И ОСТОЙЧИВОСТЬ СУДНА
Эта задача для судоводителей имеет много практических приложений. По-
садка и остойчивость очень тесно связаны друг с другом, поэтому они обычно
рассматриваются совместно.
Мкр
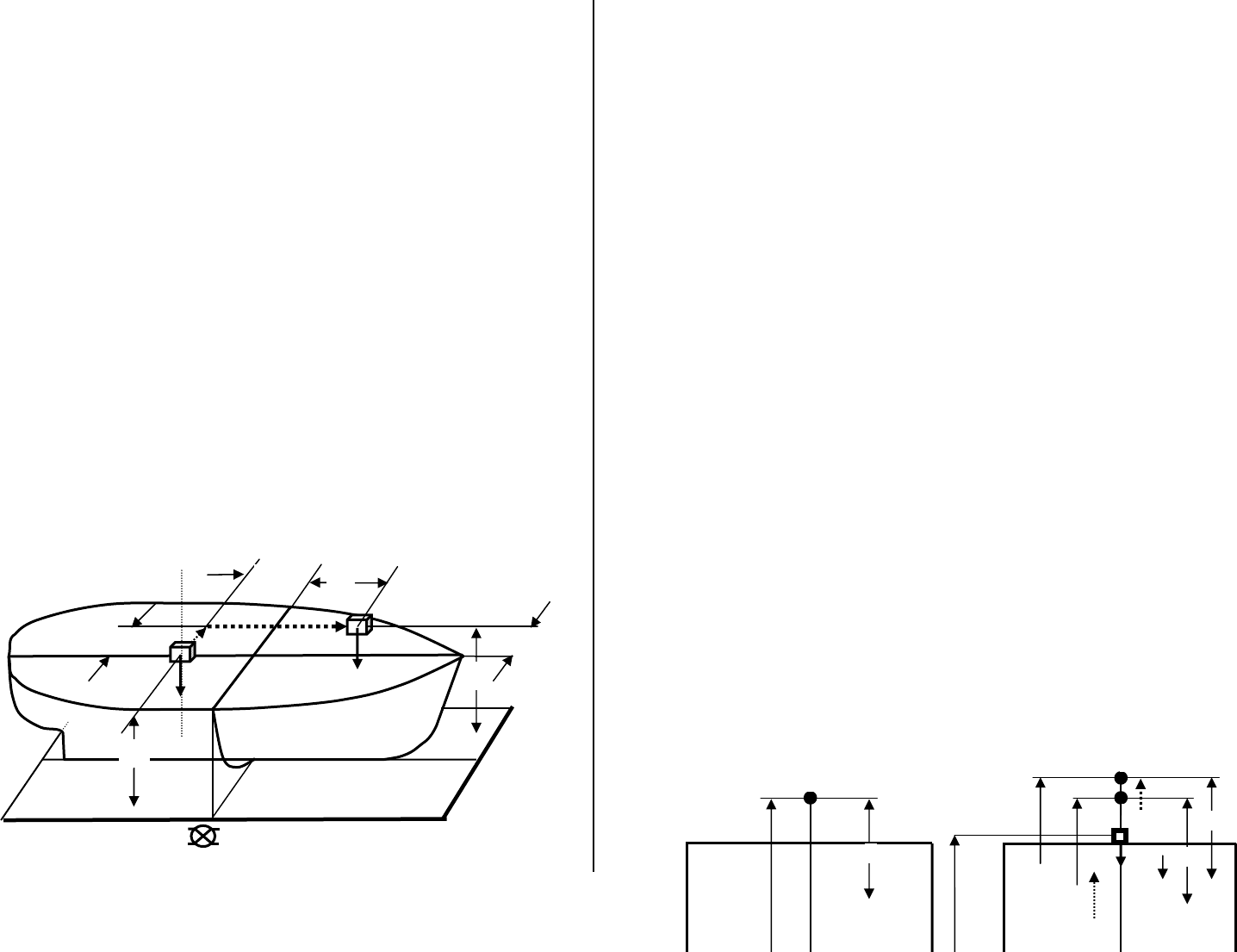
Пусть из произвольной точки A надо переместить груз р в некоторую точку B по
линии АB и оценить, как после перемещения изменится посадка и остойчивость суд-
на (см.рис. 4.1.2.1.).
Сразу следует отметить, что в такой постановке эту задачу прямо решить невоз-
можно. Для ее решения необходимо искать обходные пути, а именно, разбить весь
процесс перемещения на несколько этапов (см.рис.4.1.2.1.), рассмотреть изменение
посадки и остойчивости на каждом этапе и затем обобщить результаты.
Такими этапами будут – этап вертикального перемещения (на расстояние ⎯ℓ
z),
этап горизонтального поперечного перемещения (⎯ℓ
y) и этап горизонтального про-
дольного перемещения (⎯ℓ
x).
B
O
pж
g1
Мв
0
рж
g
рж
ΔМкр
2
1
1
1
0
⎯
ℓx
⎯
ℓy
⎯
ℓ
z
А А
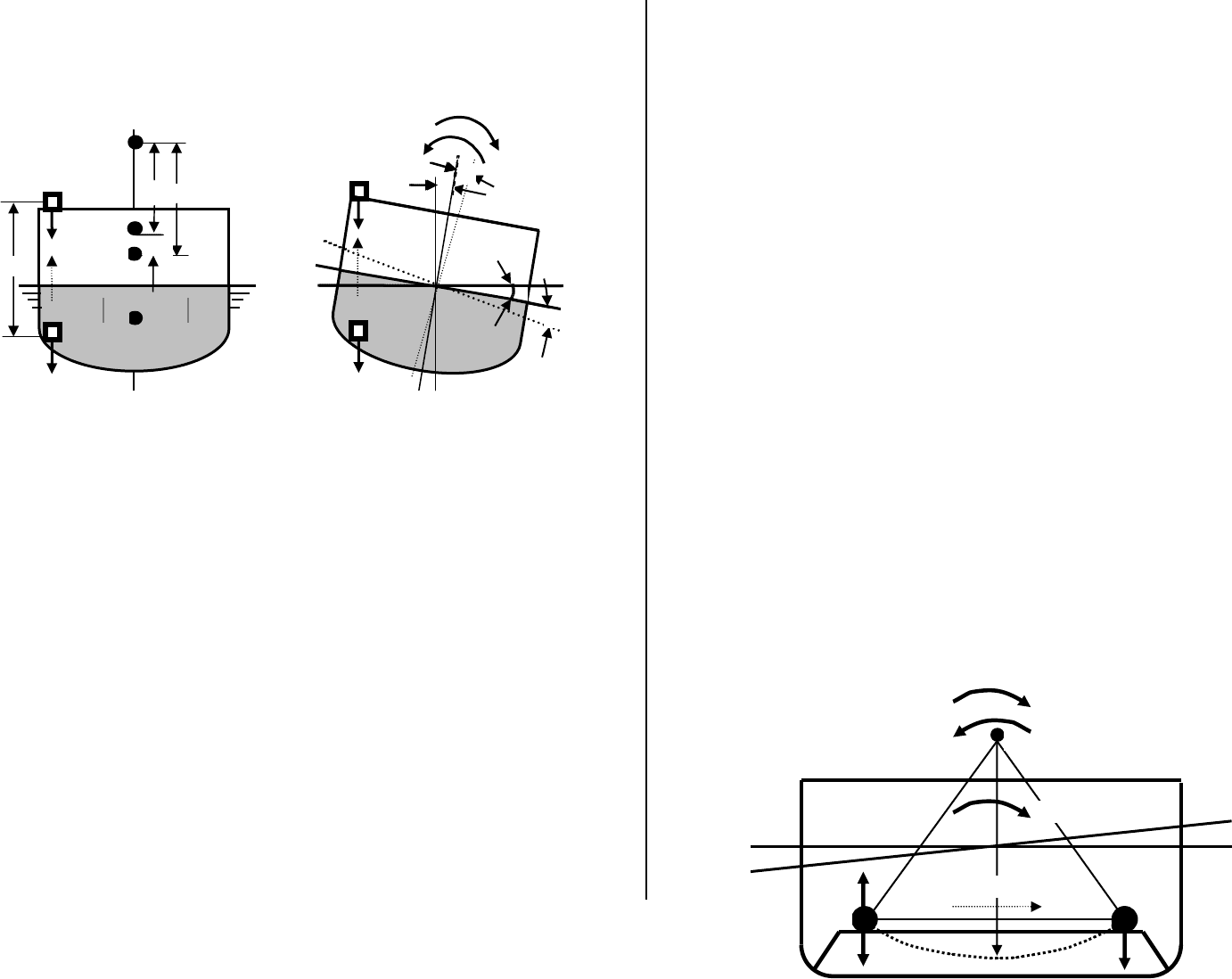
Рис. 4.1.2.1. Условные этапы перемещения груза на судне. Рис. 4.1.2.1. Условные этапы перемещения груза на судне.
Рассмотрим этап вертикального перемещения груза (см.рис.4.1.2.2.а). Рассмотрим этап вертикального перемещения груза (см.рис.4.1.2.2.а).
а) б) а) б)
Рис. 4.1.2.2. Схема вертикального переноса груза у судна без крена и с креном. Рис. 4.1.2.2. Схема вертикального переноса груза у судна без крена и с креном.
40 40
Груз р, находящийся в трюме, перемещается на палубу снизу вверх на высоту ⎯ℓ
z.
Груз р, находящийся в трюме, перемещается на палубу снизу вверх на высоту ⎯ℓ
z.
Сначала оценим изменение посадки судна, сидящего прямо, без крена. Сначала оценим изменение посадки судна, сидящего прямо, без крена.
Поскольку весовая нагрузка судна после перемещения, в целом, не изменилась и
водоизмещение D осталось прежним, то согласно условию плавучести D =γV, под-
водный объем V не изменится по величине, так как удельный вес воды γ – постоян-
ная величина. Центр величины (точка С), являясь геометрическим центром подвод-
ного объема, должен лежать в плоскости симметрии судна, находящегося в прямом
положении (в ДП). Это будет означать, что при неизменном подводном объеме по-
ложение точки С не меняется , значит, и форма подводного объема не изменится, т.е.
посадка судна не изменится.
Поскольку весовая нагрузка судна после перемещения, в целом, не изменилась и
водоизмещение D осталось прежним, то согласно условию плавучести D =γV, под-
водный объем V не изменится по величине, так как удельный вес воды γ – постоян-
ная величина. Центр величины (точка С), являясь геометрическим центром подвод-
ного объема, должен лежать в плоскости симметрии судна, находящегося в прямом
положении (в ДП). Это будет означать, что при неизменном подводном объеме по-
ложение точки С не меняется , значит, и форма подводного объема не изменится, т.е.
посадка судна не изменится.
Таким образом, при условии прямого положения после вертикального переме-
щения груза судно не получит ни крена, ни дифферента, ни изменения осадки.
Таким образом, при условии прямого положения после вертикального переме-
щения груза судно не получит ни крена, ни дифферента, ни изменения осадки.
Поскольку центр величины остался на прежнем месте, то и метацентр (точка m),
связанный с ЦВ через метацентрический радиус r, должен оставаться на прежнем
месте.
Поскольку центр величины остался на прежнем месте, то и метацентр (точка m),
связанный с ЦВ через метацентрический радиус r, должен оставаться на прежнем
месте.
Оценим изменение остойчивости судна. Оценим изменение остойчивости судна.
Согласно теореме теоретической механики о том, что, если имеется система неких
материальных тел, имеющая центр тяжести, то при перемещении какого-либо тела в
ту или иную сторону центр тяжести всей системы перемещается параллельно в ту
же сторону на величину, обратно пропорциональную соотношению массы переме-
щаемого тела и массы всей системы. Судно представляет собой систему материаль-
ных тел, имеющую ЦТ в точке G (см. рис.4.1.2.2.а). Если груз р перемещаем верти-
кально вверх, то и ЦТ судна должен переместиться параллельно из точки G в точку
G
1. Учитывая, что метацентр m остался на месте, метацентрическая высота h1 после
перемещения окажется меньше, чем h до перемещения , т.е. начальная остойчивость
изменится на величину Δh = h
1 - h. Так как h1 < h, то изменение остойчивости Δh
будет с отрицательным знаком, что означает уменьшение остойчивости. Если бы
груз перемещался вертикально вниз, то в результате параллельного опускания ЦТ G
изменение остойчивости стало бы положительным, т.е. остойчивость увеличилась.
Согласно теореме теоретической механики о том, что, если имеется система неких
материальных тел, имеющая центр тяжести, то при перемещении какого-либо тела в
ту или иную сторону центр тяжести всей системы перемещается параллельно в ту
же сторону на величину, обратно пропорциональную соотношению массы переме-
щаемого тела и массы всей системы. Судно представляет собой систему материаль-
ных тел, имеющую ЦТ в точке G (см. рис.4.1.2.2.а). Если груз р перемещаем верти-
кально вверх, то и ЦТ судна должен переместиться параллельно из точки G в точку
G
1. Учитывая, что метацентр m остался на месте, метацентрическая высота h1 после
перемещения окажется меньше, чем h до перемещения , т.е. начальная остойчивость
изменится на величину Δh = h
1 - h. Так как h1 < h, то изменение остойчивости Δh
будет с отрицательным знаком, что означает уменьшение остойчивости. Если бы
груз перемещался вертикально вниз, то в результате параллельного опускания ЦТ G
изменение остойчивости стало бы положительным, т.е. остойчивость увеличилась.
Таким образом, при вертикальном перемещении груза у прямосидящего судна
посадка не изменяется, а остойчивость изменяется в зависимости от направ-
ления перемещения : вверх остойчивость уменьшается, вниз – увеличивается.
Таким образом, при вертикальном перемещении груза у прямосидящего судна
посадка не изменяется, а остойчивость изменяется в зависимости от направ-
ления перемещения : вверх остойчивость уменьшается, вниз – увеличивается.
В соответствии с изложенной теоремой, изменение остойчивости определяется
по формуле p
В соответствии с изложенной теоремой, изменение остойчивости определяется
по формуле p
Δh = ± ----* ℓ
z (14)
Δh = ± ----* ℓ
z (14)
D D
Теперь рассмотрим изменение посадки при вертикальном перемещении груза у
судна, имеющего начальный крен. Крен на таком судне обусловлен действием кре-
нящего момента, которому препятствует (у остойчивого судна) автоматически воз-
никший восстанавливающий момент (см. рис. 4.1.2.2.б). Поскольку судно с креном
стоит неподвижно, то это означает, что М
кр = Мв, т.е. моменты друг друга уравно-
вешивают. Из метацентрической формулы (9) остойчивости
Теперь рассмотрим изменение посадки при вертикальном перемещении груза у
судна, имеющего начальный крен. Крен на таком судне обусловлен действием кре-
нящего момента, которому препятствует (у остойчивого судна) автоматически воз-
никший восстанавливающий момент (см. рис. 4.1.2.2.б). Поскольку судно с креном
стоит неподвижно, то это означает, что М
кр = Мв, т.е. моменты друг друга уравно-
вешивают. Из метацентрической формулы (9) остойчивости
М
в = D*h*sinθ Мв = D*h*sinθ
видно, что Мв прямо зависит от метацентрической высоты h. При вертикальном пе-
ремещении груза снизу вверх h уменьшается, следовательно, уменьшается и М
в.
видно, что Мв прямо зависит от метацентрической высоты h. При вертикальном пе-
ремещении груза снизу вверх h уменьшается, следовательно, уменьшается и М
в.
49 49
4.1.5. ВЛИЯНИЕ ПЕРЕКАТЫВАНИЯ ГРУЗА ПРИ КАЧКЕ НА ОСТОЙЧИВОСТЬ 4.1.5. ВЛИЯНИЕ ПЕРЕКАТЫВАНИЯ ГРУЗА ПРИ КАЧКЕ НА ОСТОЙЧИВОСТЬ
При эксплуатации судна может сложиться такая ситуация, когда во время качки
груз, сорванный с креплений, начинает перекатываться с борта на борт.
При эксплуатации судна может сложиться такая ситуация, когда во время качки
груз, сорванный с креплений, начинает перекатываться с борта на борт.
Рассмотрим вопрос, как такое перекатывание отразится остойчивости судна. Рассмотрим вопрос, как такое перекатывание отразится остойчивости судна.
m
Mкр
p
V
C
h
h1
ℓz
p
Δh
p
p
Мв
θ
Δθ
Δθ
θ
p
V
C
h
h1
Мв
Δθ
ℓz
p
Δh
p
p
θ
θ
Δθ
O
2
1
p
p
p
Mв
Mк
р
ΔMк
р

Рис. 4.1.5.1. Схема, иллюстрирующая перекатывание груза
Перекатывающийся груз, как и подвешенный, имеет возможность смещаться в сто-
рону крена, совершая при бортовой качке возвратно-поступательное движение по
плоскому настилу второго дна. При перекатке груза из положения 1 в положение 2,
по аналогии с подвешенным грузом, за счет пары сил возникает дополнительный
кренящий момент ΔМ
кр (см. рис. 4.1.5.1), который вычитается из восстанавливаю-
щего момента, снижая остойчивость судна.
При перекатывании, в результате сложения двух движений, – возвратно-
поступательного по плоскому настилу и колебательному вокруг продольной оси
судна (от бортовой качки) - истинная траектория, описываемая центром тяже-
сти перекатывающегося груза, будет представлять собой дугу окружности (на
схеме показана пуктиром), т.е. поведение ЦТ перекатывающегося груза совершенно
аналогично поведению подвешенного груза. Но подвешенный груз при этом как бы
перемещался в точку подвеса. Следовательно, рассуждая по аналогии, можно ут-
верждать, что ЦТ перекатывающегося груза перемещается в точку О – центр дуги
перекатывания (аналог точки подвеса), т.е. появление на судне перекатывающегося
груза равнозначно перемещению его ЦТ вертикально снизу вверх на высоту радиуса
R дуги перекатывания. Снижение остойчивости, в соответствии с формулой (14),
равно
p
Δh = - ---- * R
D
Таким образом, перекатывающийся груз теоретически находится не там, где
мы его видим, а где-то высоко в центре трудно определимой дуги перекатыва-
ния.
48
Из схемы видно, что силы р, перенесенные вверх из точек 1, 2, 3 и т.д., сходятся в
точке подвеса О. Это равносильно тому, что сам груз находится постоянно в точке
подвеса при любом наклонении судна. Как подвешенный груз влияет на остойчи-
вость? В результате наклонения судна ЦТ груза из точки 1 переместился в точку 2 (
по пунктирной стрелке). Чтобы показать, что в точке 1 груза уже нет, надо прило-
жить в этой точке силу, равную и противоположно направленную весу р. Тогда эта
сила вместе с весом р в точке 2 образуют пару сил, создающую дополнительный
кренящий момент ΔМ
кр, который будет иметь знак противоположный восстанавли-
вающему моменту М
в и вычитаться из него, т.е. уменьшать остойчивость. Таким
образом, подвешенный груз всегда уменьшает остойчивость из-за возможности
его перемещения в сторону крена. При этом, с позиций остойчивости подвешен-
ный груз находится не там, где мы его фактически видим (в трюме), а - в точке
подвеса.
Рассмотрим подробнее, как происходит процесс подвешивания груза (см.
рис.4.1.4.1. левый борт). Груз р находится в точке А на настиле второго дна. По
мере натяжения грузового шкентеля давление груза на второе дно уменьшается,
и в тот момент, когда сила натяжения шкентеля станет равной весу груза р, груз
как бы перемещается вертикально вверх (по пунктирной стрелке) в точку под-
веса О
1 на высоту ℓz. Таким образом, задача сводится к вертикальному переме-
щению груза снизу вверх, рассмотренному ранее в разделе 4.1.2. Остойчивость
уменьшится на величину (см. формулу 14)
p
Δh = - ----* ℓ
z
D
Скорость натяжения шкентеля обычно велика (секунды или доли секунд), поэто-
му остойчивость при подвешивании изменяется резко и скачком.
Подвесить груз – это значит резко переместить его вертикально снизу вверх
на высоту от начального положения до точки подвеса. При этом, после отрыва
груза от опорной поверхности его фактическое положение по высоте никак не по-
влияет на остойчивость – на высоте 1 м или 10 м от второго дна груз постоянно на-
гружает точку подвеса, в которой он теоретически находится.
Для дальнейшего понимания поведения подвижных грузов на примере подвешен-
ного груза необходимо уяснить, что при наклонениях судна фактическая траектория
ЦТ груза (точки 1, 2, 3 и т.д.) описывает дугу окружности, а сам груз находится в
центре этой дуги. Точно так же ведут себя и другие подвижные грузы.
Практика показывает, что снижение остойчивости при подвешивании “ собствен-
ного” груза обычно не приводило к каким-либо аварийным ситуациям. Это связано с
тем, что проектант согласует грузоподъемность судовых стрел и остойчивость судна.
Значительно более опасным является подвешивание на стреле “ чужого” груза, т.е.
груза, принятого из-за борта. В этом случае уменьшение остойчивости будет склады-
ваться из двух слагаемых – уменьшение остойчивости от подвешивания забортного
груза , определяемое формулой (14) и уменьшение от приема забортного груза на нок
стрелы. При этом судно получает значительный крен, который может спровоциро-
вать аварийную ситуацию. Этот вопрос подробно рассмотрен в работе [1]
41
При этом нарушается равновесие моментов. М
кр окажется больше Мв, хотя по ве-
личине он не изменился.
Под действием большего кренящего момента судно получит
дополнительный крен Δθ. С ростом угла крена растет его синус, что, в свою оче-
редь, вызывает рост М
в. Процесс дополнительного накренения прекращается, когда

моменты опять уравниваются по величине. Таким образом, вертикальное перемеще-
ние груза на судне, имеющем начальный крен, будет сопровождаться увеличением
крена. При вертикальном опускании груза процесс будет обратным. Изложенное по-
зволяет сделать вывод о том, что любое уменьшение остойчивости (не обязатель-
но вызванное только вертикальным перемещением снизу вверх) всегда сопровож-
дается увеличением начального крена. Это нужно учитывать, например, когда
судно имеет низко расположенное отверстие в борту выше ватерлинии. Тогда сни-
жение остойчивости может спровоцировать попадание воды во внутрь судна со все-
ми вытекающими последствиями. Следует иметь ввиду, что, чем больше начальный
крен у судна, тем заметнее приращение (увеличение или уменьшение) дополнитель-
ного крена.
Рассмотрим этап горизонтального поперечного перемещения груза (см. рис.
4.1.2.3.а).
Груз р перемещаем горизонтально с одного борта на другой в направлении, пока-
занном пунктирной стрелкой. Как было показано выше, ЦТ судна должен также пе-
реместиться горизонтально в ту же сторону из точки G
1 в точку G2. Метацентр m , в
силу неизменности подводного объема, остается на месте. Поэтому метацентриче-
ская высота h
1 до перемещения и h2 после перемещения будут равны, т.е. при гори-
зонтальном поперечном перемещении груза не происходит изменения начальной
остойчивости. Забегая вперед, заметим, что и при продольном горизонтальном
перемещении (ℓ
x) остойчивость также не будет меняться. По тем же причинам ос-
тойчивость не будет изменяться при любом направлении горизонтального пе-
ремещения груза.
а) б)
Рис. 4.1.2.3. Схема поперечного переноса груза и образование кренящего момента
42
Рассмотрим картину изменения посадки судна при горизонтальном поперечном
перемещении груза (см. рис. 4.1.2.3.а).
Показать (корректно с точки зрения теоретической механики), что груз переме-
щен с одного борта на другой, - это значит снять (уничтожить) груз на одном борту
путем приложения силы р, равной и противоположно направленной весу груза р
(см. схему на рис.4.1.2.3.а) и приложить вес груза р на другом борту. При этом воз-
никает пара сил, создающая кренящий момент и угол крена θ. В соответствии со
схемой на рис. 4.1.2.3.б,
М
кр = р*ℓу*Cosθ
Если судно стоит неподвижно после перемещения груза, то это означает, что кре-
нящему моменту М
кр противодействует равный по величине Мв, который, в соответ-
ствии с метацентрической формулой (9), равен
М
в = D*h*Sinθ
Приравнивая выражения для моментов, получим
p*ℓ
y
tgθ = ------- (15)
D*h
Переведя в градусы, получим
p*ℓ
y
θ° = 57,3*---------- (16)
D*h
Из формул (15) и (16) следует, что определить угол крена при горизонтальном попе-
речном перемещении груза можно только после предварительного расчета остойчи-
вости (h). Отсюда также следует, что угол крена и остойчивость связаны между со-
бой обратной зависимостью: чем больше остойчивость судна, тем меньше угол
крена, т.е. труднее накренить судно, что согласуется с данным ранее определением о
том , что остойчивость – это способность судна сопротивляться М
кр.
Все принципиальные положения, изложенные применительно к поперечному гори-
зонтальному переносу груза, полностью соответствуют и продольному горизон-
тальному переносу груза, с той лишь разницей, что у судна возникает дифферент,
угол которого определяется по формулам, подобным (15) и (16), где поперечная ме-
тацентрическая высота h заменена на продольную метацентрическую высоту H.
Обобщая изложенное в настоящем разделе можно утверждать, что остойчивость
изменяется только на этапе вертикального перемещения груза в зависимости
от направления перемещения, т.е. остойчивость зависит только от положения
груза по высоте. На этапах горизонтального перемещения груза (независимо от
направления) остойчивость не изменяется, а изменяется лишь посадка – у судна
появляется крен и дифферент
C
V
m
h1 h2
ℓ
y
p
p
p
Mкр
G2
G1
p
p
ℓ
y
Mкр
p
ℓ
y
=Cosθ
θ
47
4.1.4. ВЛИЯНИЕ ПОДВЕШИВАНИЯ ГРУЗА НА ОСТОЙЧИВОСТЬ
Вначале рассмотрим подвешивание “собственного” груза, т.е. груза, находящегося
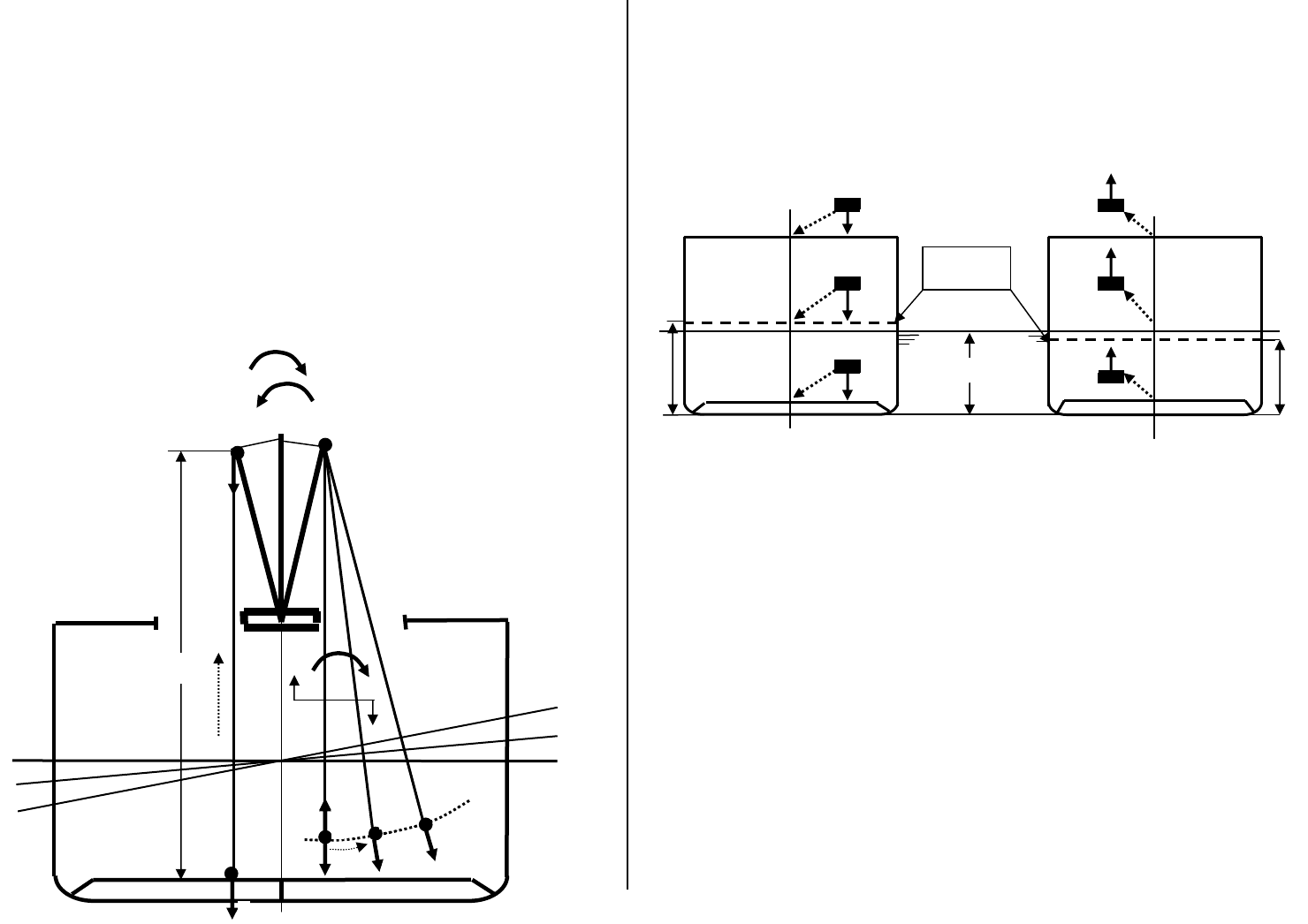
на судне и подвешиваемого судовой стрелой (см. рис.4.1.4.1.).
В прямом положении судна (ватерлиния 1-1) ЦТ груза р, висящего на грузовой
стреле в точке подвеса О, находится в точке 1. Если приложить к судну кренящий
момент, то судно получит крен (ватерлиния 2-2), автоматически возникнет уравно-
вешивающий восстанавливающий момент, грузовой шкентель (нить подвеса) станет
перпендикулярным ватерлинии, а ЦТ груза из точки 1 переместится в точку 2. Уве-
личив кренящий момент, можно переместить груз из точки 2 в точку 3 и т.д.
В теоретической механике доказывается, что перенос какой-либо силы по линии ее
действия в любую сторону и на любое расстояние совершенно не изменяет состояние
системы сил.
Рис. 4.1.4.1. Схема, иллюстрирующая подвешивание груза.
46
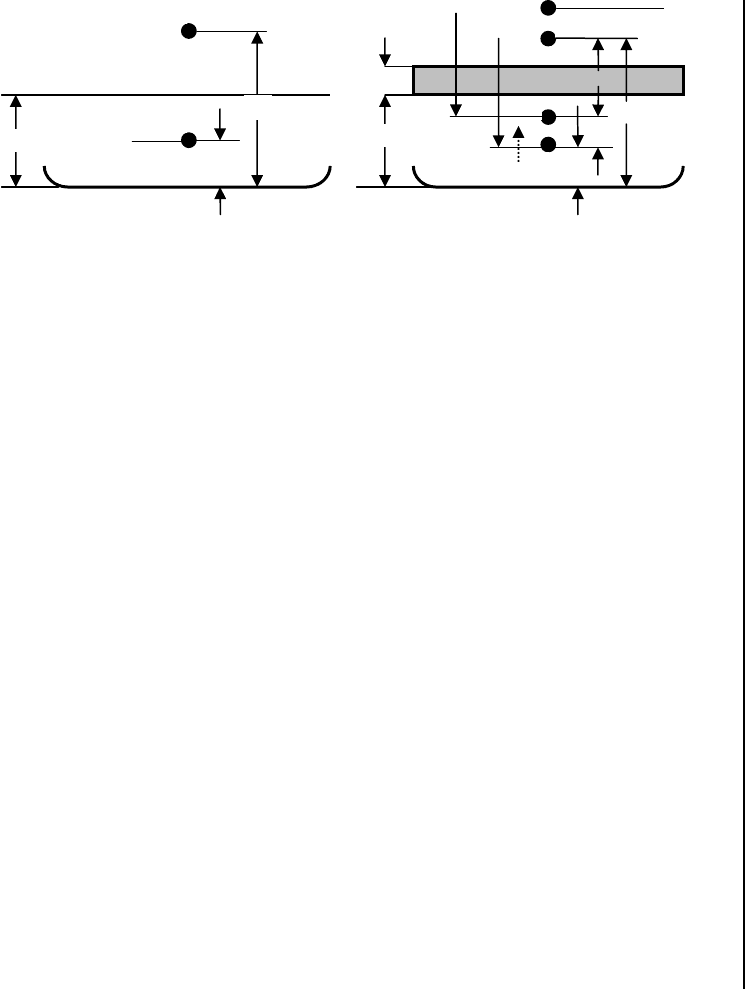
Прием груза Снятие груза
Рис. 4.1.3.3. Схема, иллюстрирующая изменение остойчивости при приеме и снятии
груза.
Поскольку рассматриваемая задача относится к приему малого груза (не более
10% от водоизмещения), то численные значения Δd/2 и h малы, по сравнению с
осадкой судна d. Еще меньше будут их разности в формуле (18). Тогда этими сла-
гаемыми можно пренебречь и считать, что z ≈ d.
Таким образом, для грубой оценки положения предельной плоскости можно
допустить, что она находится где-то близко от ватерлинии.
Обобщая изложенное, можно утверждать (см. схему на рис. 4.1.3.3.), что прием
груза выше предельной плоскости снижает остойчивость, прием ЦТ груза на
уровень предельной плоскости (в районе ватерлинии) не изменяет остойчи-
вость, прием груза ниже предельной плоскости увеличивает остойчивость. При
снятии груза картина – обратная.
На основании формулы (17) можно сделать вывод о том, что, чем выше или
ниже от предельной плоскости принимается или снимается груз, тем быстрее
изменяется остойчивость. Например, при обледенении судна (лед – это груз,
принятый высоко) необходимо путем околки льда, по возможности, быстрее
восстановить потерянную остойчивость. Для достижения приемлемой остойчи-
вости количество удаленного льда с верхних конструкций (мачт, рубок и пр.)
может быть в несколько раз меньше количества льда, удаляемого с палубы, по-
скольку ЦТ удаленного сверху льда (снятого груза) расположен значительно
выше предельной плоскости (ватерлинии), чем ЦТ льда, снятого с палубы. От-
ℓz
1
2
3
O1
p
p
p
p
p
p
Мкр
А
3
2
1
ΔМкр
Мв
1
2
3
z
=
d+Δd/2
-
h
р
Остойчивость
увеличивается
Остойчи-
вость не
Остойчивость
уменьшается
Остойчивость
увеличивается
Остойчивость
уменьшается
Остойчивость
не изменяется
р
р
р
р
р
z = d - Δd/2 - h
d
≈
z
Предельная
плоскость
сюда следует, что эффективность околки льда на палубах низкобортных судов
сранительно невелика.
Изложенное также объясняет требование “Информации об остойчивости”
начинать удаление льда, в первую очередь, с высоко расположенных конструк-
ций.
На судах часто встречаются подвижные грузы, которые имеют возможность сме-
щаться при наклонениях судна. К ним относятся – подвешенные грузы, незакреплен-
ные перекатывающиеся при качке грузы и жидкие грузы со свободной поверхно-
стью. С позиций теории остойчивости все эти грузы ведут себя примерно одинаково.
43
4.1.3. ВЛИЯНИЕ ПРИЕМА (СНЯТИЯ) ГРУЗА НА ПОСАДКУ И ОСТОЙЧИВОСТЬ СУДНА
Прием или снятие груза является одной из самых распространенных опера-
ций, выполняемых при эксплуатации судна, поэтому рассматриваемая тема
является весьма актуальной для судоводителей.
Необходимо принять груз р в произвольную точку А (см. рис. 4.1.3.1.) с координа-
тами x
a, ya и za и оценить, как изменятся посадка и остойчивость судна.
Как и в предыдущем разделе, эту задачу в такой постановке решить невозможно –
необходимо искать какие-то обходные пути, например, опять разбить на этапы.
Разобьем процесс приема груза на три условных этапа.
1-й этап. Оценить остойчивость возможно лишь в том случае, если принять груз так,
чтобы судно село ровно, не получив ни дополнительного крена, ни дополнительного
дифферента. Эта задача была уже рассмотрена ранее в разделе 3.4.1., где установле-
но, что для реализации такой посадки центр тяжести груза должен лежать на верти-
кали, проходящей через геометрический центр площади ватерлинии (точку F). Рас-
положение груза по высоте должно быть равно возвышению точки А, т.е. z
f = za .
Рис. 4.1.3.1. Схема разбивки решения задачи на этапы.
2-й этап. После оценки остойчивости на первом этапе перемещаем груз горизон-
тально из точки F поперек судна на расстояние y
f = ya. При горизонтальном переме-
щении, как известно, остойчивость не изменяется – у судна появляется крен. Этот
этап уже рассмотрен в разделе 4.1.2.
3-й этап. Груз перемещаем горизонтально вдоль судна и попадаем в нужную точку
А. При этом остойчивость не меняется – у судна появляется дифферент.
Поскольку два последних этапа рассмотрены ранее , то задача сводится к рас-
смотрению и анализу первого этапа.
44
После приема груза р в точку F на высоту z (см. рис. 4.1.3.2.б) осадка увеличится
равномерно на величину Δd, из-за этого увеличится подводный объем судна, и центр
величины (точка С) переместится в положение С
1 и, соответственно, координата zc
получит приращение Δz
c.
Зависящий от подводного объема метацентрический радиус должен изменить
свою величину и стать равным r
1. Приращение метацентрического радиуса равно Δr
= r
1-r. Так как метацентрический радиус изменился, то изменится и положение мета-
центра m, который переместится в точку m
1.
Принимая груз высоко (предположим на палубу), следует ожидать, что ЦТ судна
из точки G переместится в точку G
1, тогда zg получит приращение Δzg.
Метацентрическая высота после приема груза будет равна расстоянию h
1 от ново-
го положения метацентра m
1 до нового положения ЦТ судна G1.
Искомое изменение остойчивости равно Δh = h1-h.
Таким образом, прием груза приводит к изменению всех геометрических характе-
ристик остойчивости, т.е. к приращениям Δh, Δr, Δz
c и Δzg. Очевидно, что эти при-
ращения связаны между собой так же, как и основные геометрические характеристи-
ки остойчивости, определяемые формулой (10), т.е. можно записать, что
Δh = Δr + Δz
с – Δzg
Учитывая, что аналитическое определение этих приращений требует громоздких
математических выкладок, приведем конечный результат
p
Δh = ------ ( d + Δd/2 – h – z ) (17)
D + p
ОП
А
-xf
p
p
zа
ya
yf
xа
zf
а
)
m
h
p
m1
F
m
G1
r1
б
)
h1
h
до приема груза после приема груза
Рис.4.1.3.2. Геометрические характеристики посадки и остойчивости до и после
приема груза.
45
Проанализируем формулу (17).
На основании накопленного опыта или интуитивно можно предположить, что
прием груза на верхнюю палубу должен сопровождаться уменьшением остойчиво-
сти, прием в трюм (на второе дно) – увеличением остойчивости. Переход от плохого
к хорошему обычно сопровождается достижением какого-то нейтрального состоя-
ния. Иначе говоря, прием груза между верхней палубой и вторым дном на какой-то
высоте не должен привести к изменению остойчивости, т.е. имеется такое положение
груза по высоте, где Δh = 0. Найдем это положение. Если подставить в формулу (17)
вместо Δh нуль, то это равнозначно приравниванию нулю слагаемых в скобках. То-
гда получим
z = d + Δd/2 – h (18)
Формула (18) представляет собой уравнение плоскости, которую принято назы-
вать предельной плоскостью. Прием ЦТ груза на уровень предельной плоскости не
должен изменить остойчивость судна.
Если примем груз выше предельной плоскости, т.е. z > d + Δd/2 – h, то прираще-
ние остойчивости будет отрицательным, так как z в формуле (17) имеет знак минус,
т.е. остойчивость уменьшается. Аналогичным путем можно показать, что прием ЦТ
груза ниже предельной плоскости приводит к увеличению остойчивости.
Все изложенные выше положения для приема груза пригодны и для снятия груза,
только все будет наоборот. Снятие груза выше предельной плоскости приводит к
увеличению остойчивости, ниже – к уменьшению остойчивости. В формуле (17) знак
для р и Δd/2 поменяется с плюса на минус и сама формула примет такой вид:
p
Δh = ------ ( d - Δd/2 – h – z )
D - p
Положение предельной плоскости, в отличие от формулы (18), определяется выра-
жением
z = d – Δd/2 - h
Таким образом, чтобы судить об изменении остойчивости после приема груза не-
обходимо знать положение предельной плоскости, а для этого нужно знать осадку d
до приема груза, рассчитать половину изменения осадки Δd/2 после приема груза по
формуле (6) Δd = p / q (см. раздел 3.4.1.) и рассчитать метацентрическую высоту h
до приема груза по формуле (10) h = r + z
c – zg.
Расчеты по определению положения предельной плоскости нужно выполнять
для каждого случая загрузки судна, что потребует от судоводителей определен-
ных затрат времени. Поэтому, важным для практики вопросом является знание
примерного положения предельной плоскости, позволяющее хотя бы грубо оце-
нивать остойчивость, не прибегая к специальным вычислениям, например, при
проведении грузовых операций.
zc
Δz
g
r
d
G
z
g
С
Δd
С
z
d
С1
G
z
g
Δzc
zc
r
