Байгунусов В.Б. Судоводителям о плавучести и остойчивости судна

Подождите немного. Документ загружается.

чимся рассмотрением последнего способа, так как он чаще применяется на новых

судах и несколько проще первого.

Универсальная диаграмма статической остойчивости представляет собой со-

вокупность кривых, показанных на рис. 4.2.2.1.а.

а) б)

ℓ,(

м)

Типовая таблица расчета координат ЦТ судна

θ˚

0 10 20 30 40 50 60 70 80 90 0 10 20 30 40

Рис. 4.2.2.1. Универсальная диаграмма статической остойчивости (а)

и построение ДСО (б)

УДСО разрабатывает проектант судна и помещает ее в “Информацию об остойчиво-

сти ”. УДСО представляет собой совокупность кривых равных водоизмещений D

судна, построенных на осях ℓ, z

g и θ˚ (на логарифмической шкале).

Принцип работы с УДСО состоит в том, что вычисляются в табличной форме (см.

раздел 3.3.) водоизмещение D для заданного случая нагрузки и соответствующая

ему координата ЦТ судна z

g. Методом интерполяции (пропорционально между кри-

выми) по найденному водоизмещению строится на УДСО кривая равных водоиз-

мещений (на рис.4.2.2.1.а показана пунктирной линией). Затем на оси z

g откладыва-

ется найденная координата ЦТ и ее значение соединяется прямой (показана

пунктиром) с началом координат. Восстановив перпендикуляры из значений углов

крена на горизонтальной оси до пересечения с построенной кривой водоизмещений,

находим плечи ℓ, соответствующие конкретным углам крена и равные расстояниям

от кривой водоизмещения до наклонной прямой. Отложив.эти плечи на соответст-

вующих углах ДСО (см. рис. 4.2.2.1б) и соединив их плавной кривой, получим ДСО.

статические моменты статьи относительно миделя (M

x) и ОП (Mz) и занесем их,

соответственно, в столбцы 6 и 7. Просуммировав столбцы 3, 6 и 7, получим дедвейт

и статические моменты дедвейта относительно миделя и ОП. Если теперь просум-

мировать данные по дедвейту с аналогичными данными проектанта по судну порож-

нем, взятыми из “Информации об остойчивости”, то получим водоизмещение судна

D для данного случая загрузки и его суммарные статические моменты Σ

Mx относи-

тельно миделя и ΣM

z относительно ОП. Разделив суммарные статические моменты

на водоизмещение, получим искомые значения x

g и zg, которые заносим в 4-й и 5-й

столбцы строки “Итого судно в случае нагрузки”.

Таблица 3.3.1.

№

п/п

Наименование статей нагрузки

Вес статьи

pi,

(т)

Плечи относи-

тель-

но миделя и ОП

Статические момен

-ты относительно ми-

деля и ОП

(м)

Mx=pixi

(тм)

z=pizi

(тм)

1 2 3 4 5 6 7

1 Цистерна дизтоплива № 1 20 15 1 300 20

2 Цистерна дизтоплива № 2 50 10 2 500 100

3 Цистерна пресной воды №1 40 5 1 200 40

4 Трюм № 1 100 8 3 800 300

I - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

Итого дедвейт

(просуммировать столбцы)

Σpi

- -

Σ(pixi) Σ(pizi)

Cудно порожнем

(переписать из”Информации об

остойчивости”)

Do xgo zgo Do*xgo Do*zgo

Итого судно в случае нагрузки

(рассчитать)

D =Do+Σpi xg

zg ΣMx ΣMz

Do * xgo + Σ(pi*xi) ΣMx

xg = =

Do + Σpi D

Cледует заметить, что наиболее трудоемким процессом является определение плеч

статей нагрузки. Описанный выше процесс их нахождения больше пригоден для

трюмов, поскольку форма трюма более похожа на ящик, чем цистерн (особенно

днищевых). Для цистерн найти плечо z

i будет легче, быстрее и точнее, если предва-

рительно построить по данным “Информации об остойчивости” для каждой цистер-

ны специальные вспомогательные графики, описывающие зависимость веса статьи

от ее плеча z

Отметим, что плечи x

i очень мало зависят от количества груза в каждой статье из-

за вертикальности переборок, поэтому их, с несущественной погрешностью, можно

принимать такими же, как для 100% груза, т.е. брать из “Информации”.

Вычисленные координаты x

g и zg в дальнейшем будут использованы в разных це-

лях:

xg – для оценки посадки судна, zg – для оценки остойчивости.

θ˚

zg,(м)

ℓ40

ℓ30

ℓ20

ℓ10

ℓ, (м)

ℓ10

ℓ20 ℓ30 ℓ40

θ˚

3.4. ПРАКТИЧЕСКИЕ ЗАДАЧИ, РЕШАЕМЫЕ В ТЕОРИИ ПЛАВУЧЕСТИ

3.4.1. ОПРЕДЕЛЕНИЕ ИЗМЕНЕНИЯ ОСАДКИ ПОСЛЕ ПРИЕМА (СНЯТИЯ) ГРУЗА

Настоящая задача разрешима при условии, что судно сидит на ровном киле без

крена или имеет очень малый дифферент.

Принимаемые на судно грузы можно условно разделить на две категории: грузы

малые (не более 10% от водоизмещения) и грузы большие. Необходимость такого

деления будет понятна в дальнейшем.

Решим задачу для приема малого груза.

а) б)

γv

d носовые кормовые

обводы судна

в)

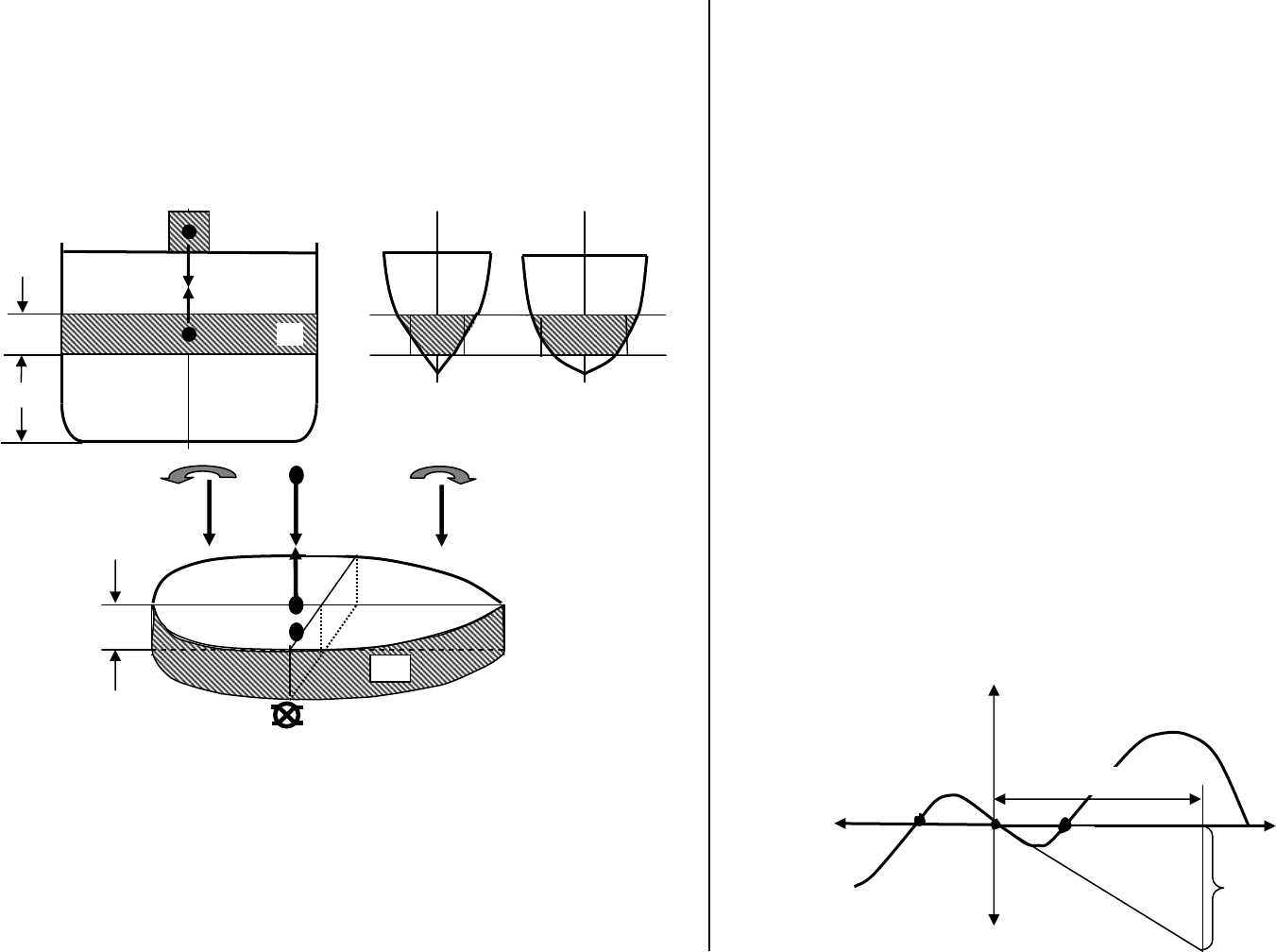
Рис. 3.4.1.1. Графическое пояснение задачи об изменении осадки после приема мало-

го груза

Примем на судно малый груз р с ЦТ в точке g так, чтобы после приема крен и диф-

ферент не изменились, т.е. судно село ровно с одинаковым изменением осадки Δd

(см. рис. 3.4.1.1.а). При этом, в воду войдет дополнительный объем v (он выделен) и,

соответственно, появляются дополнительные силы поддержания γv, компенсирую-

щие принятый груз, т.е. по аналогии с условием плавучести имеем

p = γv

остойчивость высокая, если кривая вогнутая и имеет точку перегиба, то начальная

остойчивость низкая. На этом основании, можно предсказать поведение судна на

взволнованном море – бортовая качка у судна, имеющего выпуклую форму ДСО,

будет резкой (остойчивость высокая), и наоборот, у судна с вогнутой формой

ДСО следует ожидать более плавной качки.

Вогнутость восходящего участка ДСО может увеличиваться и, в конце концов,

выродиться в S – образную кривую (см. рис.4.2.1.5 правый борт). Применим опи-

санный выше прием нахождения h. Проведем из начала координат касательную к

кривой ДСО правого борта, отложим на оси углов 1 радиан и восставим перпендику-

ляр до пересечения с касательной. Полученный отрезок h направлен вниз, т.е. будет

отрицательным (напомним, что на правом борту положительные значения направле-

ны вверх). Таким образом, S – образная ДСО характеризует отрицательную на-

чальную остойчивость. Как видно из ДСО, судно, имеющее отрицательную на-

чальную остойчивость (когда метацентр лежит ниже ЦТ судна и М

в имеет тот же

знак, что и М

кр), прямо стоять не будет, а лежит на правом борту с креном, соответ-

ствующим точке 1. Если приложить к судну такой же кренящий момент на левый

борт, то судно медленно и плавно перевалится на левый борт на тот же угол крена.

Любая попытка спрямить крен судна с отрицательной начальной остойчиво-

стью бесполезна, так как в точке 0 судно находится в неустойчивом состоянии. На

ходу такое судно будет валким, т.е. будет идти с креном на какой-либо борт, пока на

него не подействует кренящий момент другого знака, после чего судно перевалится и

будет идти с креном на другой борт. Переваливание судна с борта на борт имеет

динамический характер. Как будет установлено далее, динамические углы крена зна-

чительно превышают статические. При этом, в момент остановки после перевалива-

ния возникают большие инерционные силы, пытающиеся сместить тяжеловесные

грузы так же, как и при резкой качке. Отрицательная начальная остойчивость обычно

не приводит к опрокидыванию судна, т.к. оно достаточно хорошо сопротивляется

наклонению на углах крена, превышающих углы в точке 1 или 2.

ℓ

,(м)

Левый борт Правый борт

0º 0º

- h

ℓ

,(м)

с1

γv

Δd

Mдиф

1 радиан =57,3º

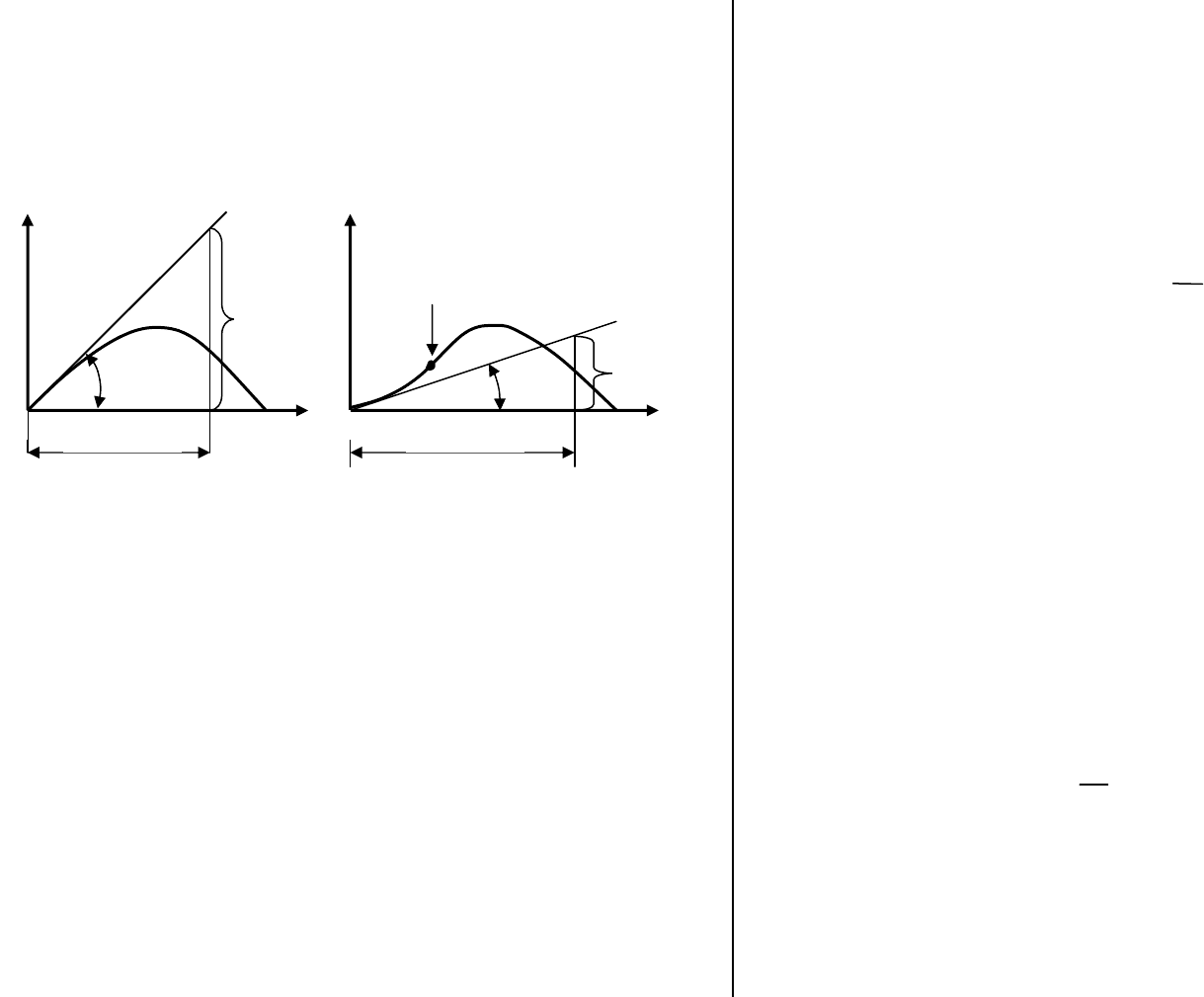
Рис. 4.2.1.5. Диаграмма статической остойчивости у судна, имеющего отрицатель-

ную начальную остойчивость.

Начальная остойчивость охватывает диапазон углов крена от 0º до 10º, ДСО – от

0º до угла заката. Следовательно, начальная остойчивость является частным случаем

остойчивости на больших углах и должна каким-то образом проявить себя в ДСО.

а) б)

ℓ

,(м) ℓ,(м)

0º 0º

Рис. 4.2.1.4. Схема, показвающая влияние формы ДСО на начальную остойчивость

На рис. 4.2.1.4 а и б показаны две ДСО, имеющие одинаковые основные параметры

в(max), θmax, θзак, но отличающиеся формой восходящего участка ДСО. На

рис.4.2.1.4.а восходящий участок выпуклый и не имеет точки перегиба (точки изме-

нения кривизны), а на рис.4.2.1.4.б – вогнутый и имеет точку перегиба. Проведем

касательную из начала координат к кривой ДСО. На том участке, где касательная

практически сливается с кривой ДСО (это примерно соответствует 10º), действуют

основные положения начальной остойчивости. Далее разрыв между касательной и

кривой ДСО быстро возрастает и начинают действовать законы остойчивости на

больших углах крена. Очевидно, что интенсивность нарастания остойчивости в на-

чальный период наклонения (до 10º) заметно выше у выпуклого восходящего участка

ДСО (рис.4.2.1.4.а). Изменение интенсивности, описанной в виде какой-либо кри-

вой, выражается тангенсом угла наклона касательной к этой кривой. Значит, об из-

менении начальной остойчивости можно судить по величине угла α наклона каса-

тельной. На этом основании, можно установить (доказательство опускаем), что с

помощью ДСО можно графически определить метацентрическую высоту h следую-

щим образом. Следует провести из начала координат касательную к кривой ДСО,

построенной в масштабе плеч, затем отложить на оси углов крена один радиан, рав-

ный 57,3º, и из этого угла восставить перпендикуляр Тогда, отрезок от точки пере-

сечения перпендикуляра с касательной до оси углов будет равен метацентрической

высоте h.

Сопоставляя рис. 4.2.1.4. а и б, убеждаемся, что наличие вогнутости восходящего

участка ДСО свидетельствует о пониженной начальной остойчивости.

Таким образом, по форме кривой ДСО можно судить о том, какова начальная

остойчивость судна – если кривая выпуклая (нет точки перегиба), то начальная

“Вырежем” вошедший в воду объем (см. рис.3.4.1.1.в) и определим его. Если

борта у судна прямостенные, то тогда вырезанное тело является цилиндром с одина-

ковыми площадями оснований S в виде ватерлиний и высотой Δd. Тогда, объем ци-

линдра равен v = S*Δd

После подстановки v в p = γ*v, получим

Δd = , (м) (5)

γ*S

Задача решена в предположении, что судно имеет прямостенные вертикальные

борта. У реальных судов прямостенность бортов имеет место, в основном, в средней

части; в оконечностях же, как правило, имеется развал бортов (см. рис. 3.4.1.1 б).

Учитывая, что при приеме малого груза, осадка изменяется мало, непрямостенно-

стью бортов в оконечностях можно пренебречь, при этом погрешность решения

будет незначительной.

При приеме больших грузов эта погрешность значительно возрастает. Если учиты-

вать непрямостенность бортов, то площади оснований вырезанного тела будут раз-

ными, и это тело будет представлять собой усеченный конус неправильной формы,

вычисление объема которого встретит значительные трудности, и задачу нужно ре-

шать другим путем.

Таким образом, для решения задачи по формуле (5) для малого груза необходимо

знать площадь ватерлинии S, величина которой зависит от формы корпуса и осадки

судна и вычислить которую можно только с помощью теоретического чертежа, т.е.

проектант должен рассчитать и предоставить судоводителям зависимость S от d.

Однако, проектант обычно приводит в “Информации об остойчивости” другой пара-

метр: q = 0,01 γ*S (т/м) – количество принятых (снятых) тонн груза, изменяющих

осадку на 1 см. Тогда формула (5) упрощается, и решением поставленной задачи

является

Δd = , м (6)

Следует заметить, поскольку площадь ватерлинии S зависит от осадки, то и про-

порциональное S значение q также будет зависеть от осадки d, т.е. q – величина не

постоянная, и это надо учитывать при ее выборе, т.е.снимать с графика.

Определим положение ЦТ груза (точки g), при котором обеспечивается посадка

судна без крена и дифферента. Ранее было установлено, что силы поддержания судна

приложены в центре величины (точке С), который является геометрическим центром

подводного объема. Очевидно, что и в вошедшем в воду объеме дополнительные

силы поддержания γv (см. рис. 3.4.1.1.в) также приложены в геометрическом центре

0 0

1 радиан =57,3º 1 радиан =57,3º

Точка перегиба ДСО

выре-занного объема - точке С

1. Если предположить, что изменение осадки Δd не-

зна-чительно (Δd→0), то геометрический центр объема вырождается в геометриче-

ский центр площади ватерлинии (точку F). Тогда, после размещения груза в нос или

корму от точки F, возникают пары сил, создающие дифферентующие моменты М

диф

на нос или на корму и вызывающие появление дифферента.

Исключить дифферент и крен можно, разместив ЦТ груза на вертикали, ле-

жащей в ДП и проходящей через геометрический центр площади ватерлинии F.

Ранее было отмечено, что решение задачи для приема (снятия) большого груза (бо-

лее 10% от водоизмещения) должно отличаться от решения для малого груза из-за

непрямостенности бортов в оконечностях судна.

Для решения задачи об изменении осадки при приеме (снятии) большого груза

необходимо воспользоваться судовой документацией и использовать график, отра-

жающий зависимость водоизмещения судна D от осадки d. Этот график (см.

рис.3.4.1.2.) называется грузовым размером. Он строится проектантом и приводится

в “Кривых элементов теоретического чертежа” (см. выше раздел 2.2).

d, (м)

Δd

D, (т)

D p

1 = D + p

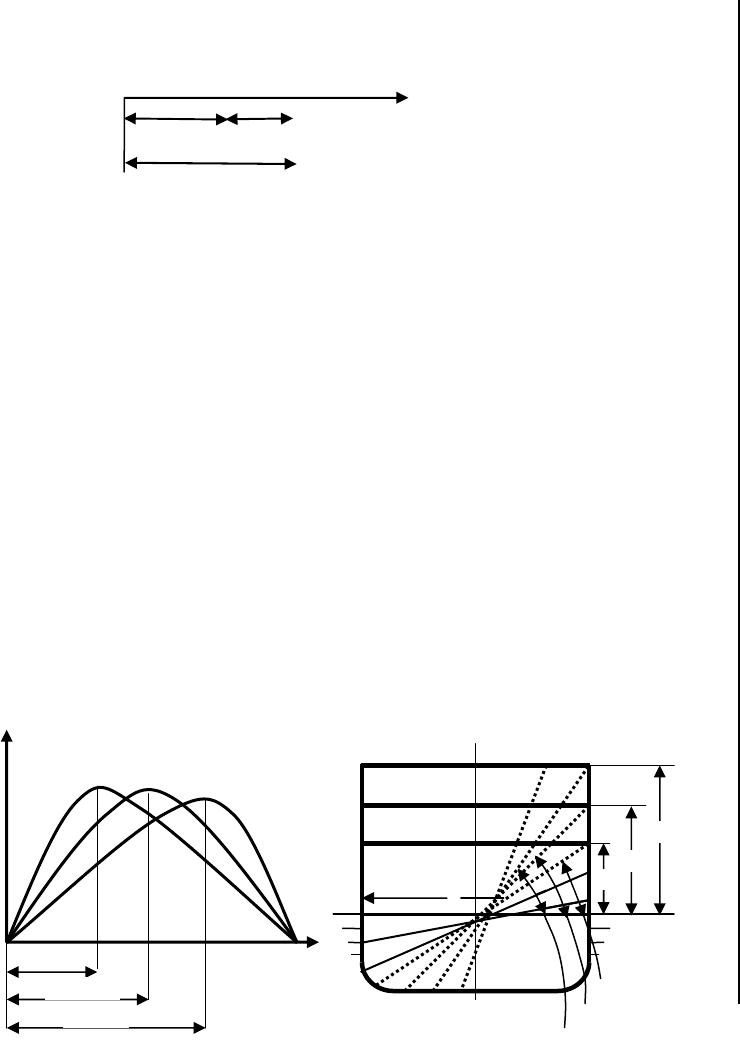
Рис. 3.4.1.2. Грузовой размер и определение изменения осадки после приема

большого груза

Отложив на грузовом размере водоизмещение D (до приема груза), находим соот-

вет-ствующую ему осадку d. Прибавив к водоизмещению принятый большой груз р,

находим новое водоизмещение D

1 и соответствующую ему осадку d1. Разность оса-

док d

1 и d дает искомое решение.

Грузовой размер, как и все “Кривые элементов теоретического чертежа”, построен

для судна, сидящего на ровном киле без крена, поэтому представленное решение

применимо только для прямой и бездифферентной посадки судна.

Для сокращения объема вычислительной работы по изложенной задаче проектант

обычно разрабатывает для судоводителей, т.н. грузовую шкалу, представляющую

нечто подобное номограмме или логарифмической линейке, в которую уже заложе-

ны в цифрах грузовой размер, q и пр. в зависимости от осадки судна.

Таким образом, использование грузовой шкалы дает судоводителю возможность

решать изложенные выше задачи для ровного и прямого положения судна или судна

с очень малым дифферентом без специальных вычислений.

Учитывая жизненно важное (для безопасности судна) значение угла максимума ДСО

(θ

max), выясним, от каких факторов зависит положение максимума ДСО.

а) б)

1 2 3

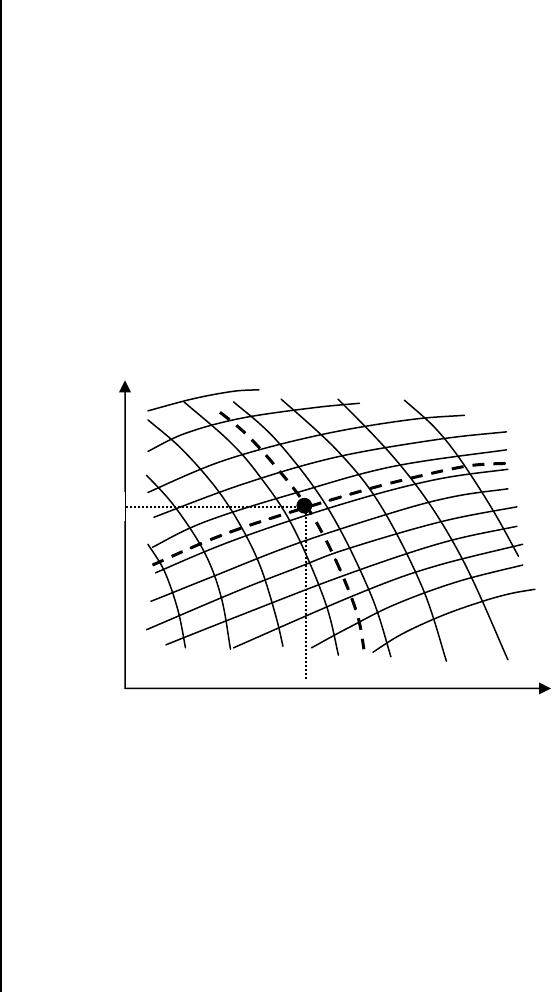
Рис.4.2.1.3. К определению положения угла максимума ДСО

На рис. 4.2.1.3.а показаны три ДСО, имеющие одинаковые параметры M

в(max) и θзак,

но различные углы максимума ДСО (θmax). Очевидно, что более безопасной будет

эксплуатация судна, имеющего больший предельный гарантирующий безопасность

угол

θmax (ДСО 3). Ранее в разделе 4.1.1. и в формулах (12) и (13) было показано, что

остойчивость судна очень быстро (в кубе) растет с увеличением ширины ватерлинии

b (см. рис. 4.2.1.3.б). По мере наклонения судна ширина ватерлинии увеличивается

до некоторого максимума, а затем начинает сокращаться, т.е. изменение ширины

ватерлинии и, следовательно, остойчивости имеет одинаковый характер. Иначе гово-

ря, кривая ДСО повторяет характер изменения ширины ватерлинии. Наибольших

значений ширина ватерлинии достигает тогда, когда либо угол соединения палубы и

борта начинает входить в воду, либо скула выходить из воды (это зависит от соот-

ношения ширины судна, его высоты борта и осадки). Чаще всего, в воду раньше

входит палуба. Значит, угол крена, при котором палуба начинает входить в воду,

является углом максимума ДСО. В свою очередь, этот угол зависит от высоты над-

водного борта (

F¹, F², F³). Чем выше надводный борт, тем больше угол максимума

ДСО. Поэтому эксплуатация низкобортных (маломерных) судов опаснее и аварий-

ность их больше, чем высокобортных.

К уменьшению высоты надводного борта может привести и перегрузка судна,

опасная не только уменьшением запаса плавучести (см. раздел 3.5.), но и более ран-

ним возможным опрокидыванием судна.

θ°

Мв

θ¹max

θ²max

θ³max

F³

F²

θ¹max

F¹

θ²max

θ³max

С помощью ДСО можно оценить предельные возможности судна сопротивляться

действию кренящего момента, иначе говоря, определить тот максимальный креня-

щий момент, который еще может выдержать судно. При этом, M

кр(max) должен быть

равен M

в(max). Если Mкр(max) > Mв(max), то горизонтальная прямая, параллельная оси

углов пройдет выше и нигде не пересечет ДСО, поэтому кренящий момент будет

всегда превосходить восстанавливающий и процесс наклонения судна будет продол-

жаться до опрокидывания судна, если не предпринять каких-либо мер по устранению

кр.

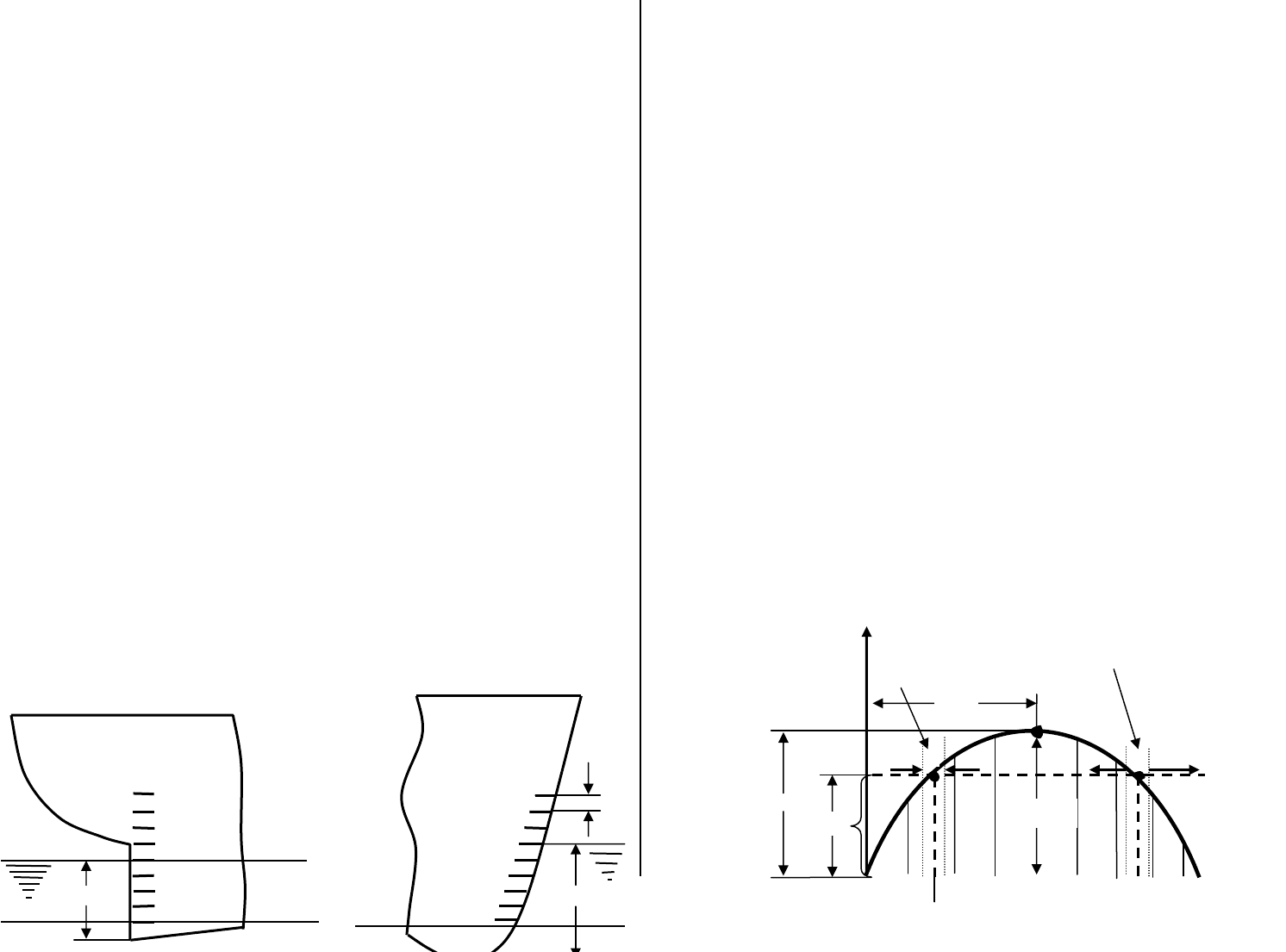
В точке 1 имеет место равенство моментов - кренящего и восстанавливающего

(см. рис.4.2.1.2.). Это равенство означает, что судно будет стоять неподвижно с уг-

лом крена θ. Такое же равенство наблюдается и в точке 2.

Рассмотрим, как поведет себя судно в этих точках равновесия при небольшом

качании. Увеличим и уменьшим крен на пару градусов в окрестности точки 1. Если

увеличим угол крена в точке 1, то восстанавливающий момент окажется больше кре-

нящего. Под действием большего восстанавливающего момента судно будет стре-

миться восстановиться, т.е. уменьшить крен (показано стрелкой влево). Если

уменьшим крен, то кренящий момент станет больше восстанавливающего, и судно

будет стремиться увеличить крен (показано стрелкой вправо). Таким образом, при

отклонение от равновесного состояния в точке 1 на тот или другой борт судно посто-

янно стремится занять наклонное положение, соответствующее углу в точке 1. Это

означает, что точка 1 является точкой устойчивого равновесия. По-другому ведет

себя судно в точке 2. При увеличении крена кренящий момент окажется больше вос-

станавливающего, и судно будет стремиться еще больше увеличить крен (показано

стрелкой вправо). При уменьшении крена восстанавливающий момент окажется

больше кренящего, следовательно, судно стремится восстановиться. Таким образом,

точка 2 является точкой неустойчивого равновесия, т.е. в этой точке судно поведет

себя непредсказуемо – при малейшем отклонении от угла крена, соответствующего

углу в точке 2, судно будет либо восстанавливаться, либо крениться дальше, но сто-

ять в этой точке не будет. Поэтому принимать ее во внимание нельзя.

Выполненный анализ поведения судна при его наклонениях можно распространить

на любую точку ДСО. Это позволяет утверждать, что любая точка на восходящем

участке ДСО (в диапазоне углов крена от 0 до θ

max) является точкой устойчивого

равновесия, т.е. при кренящих моментах, соответствующих восходящему уча-

стку ДСО, судно всегда остановится и будет стоять с креном. В любой точке на

нисходящем участке ДСО (в диапазоне углов крена от θ

max до θзак) судно поведет

себя неопределенно - может как восстановиться до угла крена θ (в точке 1), так

и опрокинуться, если не будет устранен кренящий момент.

На основании изложенного, можно утверждать, что безопасность судна гаран-

тируется только до углов крена, соответствующих углу максимума ДСО (θ

max).

При больших углах безопасность судна может быть обеспечена только в том

случае, если по каким-либо неизвестным причинам исчезнет кренящий момент.

Таким образом, ДСО позволяет без всяких расчетов оценить угол крена, при ко-

тором экипажу без риска для жизни рекомендуется покидать судно.

3 .4. 2. ОПРЕДЕЛЕНИЕ ОСАДОК СУДНА НОСОМ И КОРМОЙ

Во время эксплуатации бездифферентная посадка судна является скорее исключе-

нием, чем правилом. Поэтому значительно больший интерес для практики представ-

ляет определение осадок судна носом d

н и кормой dк, определяющих дифферент при

заданной

загрузке судна.

Для определения осадок у судна с дифферентом проектант разрабатывает и при-

водит в “Информации об остойчивости” “Диаграмму осадок носом и кормой”.

Диаграмма включает в себя два семейства кривых равных водоизмещений D и рав-

ных x

g, построенных на осях осадок носом dн и кормой dк (см. рис. 3.4.2.1.).

dн

xg = 1,0м

1,5м

2,0м

2,5м

3,0м

3,5м

4,0м

4,5м

5,0м

D = 1000Т 1100Т 1200Т 1300Т 1400Т 1500Т

к dк

Рис. 3.4.2.1. Диаграмма осадок носом и кормой

Рассчитав в табличной форме D и xg и проведя по их значениям кривые (интер-

поляцией), как показано на рис. 3.4.2.1., находим по точке пересечения кривых иско-

мые значения осадок носом d

н и кормой dк.

Диаграмма осадок может быть представлена проектантом в другом виде: на осях

координат могут быть отложены D и x

g, а оба семейства кривых являются кривыми

равных осадок носом и кормой. Тогда, отложив на осях рассчитанные значения D и

g,, через точку пересечения параллельно каждому семейству проводим путем интер-

поляции кривые осадок. От этого принципиально ничего не меняется.

dн

Вместо x

g может быть отложено ΣMx. Учитывая, что xg = ΣMx/D, от этого также

принципиально ничего не меняется – сокращается лишь одно действие (не надо де-

лить на водоизмещение).

Диаграмму осадок можно использовать и для решения обратной задачи: по из-

вест-ным осадкам носом и кормой до и после приема груза можно по разности водо-

измещений найти количество принятого груза.

3.4.3. ОПРЕДЕЛЕНИЕ ОСАДОК ПО МАРКАМ УГЛУБЛЕНИЯ

Осадки судна, определяемые по диаграммам осадок являются расчетными или

теоретическими осадками, которые измеряются от плоскости действующей ва-

терлинии до ОП.

Для непосредственной визуальной оценки осадок носом и кормой на судне пре-

дусмотрены марки углубления – деления, нанесенные на обоих бортах на форштев-

не и ахтерштевне и показывающие фактические осадки, которые отличаются от

теорети-ческих тем, что измеряются от плоскости действующей ватерлинии до наи-

более заглубленной точки на носовой и кормовой части днища. На судне ниже ОП

могут быть расположены различные конструкции - брусковый киль, различного рода

выступающие части, конструктивный дифферент судна (на нос или на корму), пре-

дусмотренный проектом , и пр.

Существуют две системы мер измерения осадок на марках углубления: метриче-

ская и дюймовая, применяемая на некоторых судах иностранной постройки. Если

цифры между делениями арабские, то расстояние между делениями и высота цифр

равны 100 мм, если же – римские, то это расстояние равно 6 дюймов = 0,5 фута = 152

мм. Значения арабских цифр на марках даются в дециметрах. Например, если над

уровнем воды видна цифра 48, то это означает, что фактическая осадка равна 4 мет-

рам 80 см.

По теоретическим осадкам можно найти фактические и наоборот. Для этого на

диаграмме осадок предусмотрены специальные шкалы фактических осадок.

100мм

14 14

13 13

12 12

11 11

10 10

9 9

Рис. 3.4.3.1. Марки углубления на судне.

Рассмотрим какими свойствами обладает ДСО.

ДСО показывает (см. рис.4.2.1.1), что остойчивость судна (М

в или ℓ) с ростом

угла крена сначала увеличивается, достигает максимума, а затем уменьшается до

нуля.

Угол крена, при котором М

в = 0 или ℓ = 0, называется углом заката ДСО (обычно

зак >60°). Восстанавливающий момент положителен, т.е. направлен против Мкр, и

судно остойчиво только до угла заката. При крене большем, чем θ

зак, восстанавли-

вающий момент меняет свой знак на обратный и направлен в сторону действия кре-

нящего момента, т.е. после устранения М

кр отрицательный восстанавливающий мо-

мент не даст судну возвратиться в начальное положение.

Таким образом, угол заката ДСО показывает, до каких углов крена судно бу-

дет остойчивым и может восстанавливаться, если убрать М

кр.

Кроме угла заката θзак, другими основными характеристиками ДСО являются:

- угол крена θ

max, которому соответствует максимум ДСО;

- максимальный восстанавливающий момент Мв(max) или его плечо ℓ(max).

Рассмотрим, какие практические задачи можно решать с помощью ДСО.

Мв,(тм)

оп

dк = 1,2м

dн = 1,3 м

θ°

Мкр

1 2

Mв(max)

Mкр(max)

θmax

θзак

Точка устойчи-

вого равновесия

Точка неустойчивого

авновесия

0 10 20 30 40 50 60 70 80

Рис.4.2.1.2 Схема к определению θ и M

кр(max) с помощью ДСО

С помощью ДСО можно без специальных вычислений определить угол крена θ по

известному кренящему моменту М

кр (см. рис. 4.2.1.2.). Для этого нужно на верти-

каль-ной оси моментов отложить М

кр, провести горизонтальную прямую, парал-

лельную оси углов крена, и из точки 1 пересечения с ДСО опустить перпендикуляр

на ось углов. Проведенная прямая, параллельная оси углов (показана штриховой ли-

нией), по существу, в общем виде представляет собой зависимость M

кр от θ, и ее

параллельность указывает на то, что величина M

кр не зависит от угла крена.

Если ДСО построена в масштабе плеч, то на вертикальной оси должно быть отло-

жено плечо кренящего момента ℓ

кр = Mкр / D .

4.2.1. СВОЙСТВА И ПРАКТИЧЕСКОЕ ИСПОЛЬЗОВАНИЕ ДИАГРАММЫ СТАТИЧЕСКОЙ

ОСТОЙЧИВОСТИ

После подстановки формулы (23) в М

в = D*ℓ получим искомую зависимость

в = f (θ). Учитывая, что в формулу (23) входит координата ЦТ судна zg, которая

прямо связана с водоизмещением D и зависит от него, то в выражении М

в = D*ℓ во-

доизмещение D выступает в качестве постоянной величины (D = const), когда каж-

дому конкретному значению ℓ будет соответствовать конкретное значение М

в для

заданного водоизмещения D. Это означает, что на вертикальной оси ДСО можно от-

кладывать или плечо восстанавливающего момента ℓ

(м) или непосредственно сам

восстанавливающий момент М

в (тм), - от этого ДСО не меняется, а меняется лишь

масштаб шкалы вертикальной оси (метры или тонно-метры). Если ДСО построена в

масштабе плеч и нужно перейти к масштабу моментов, необходимо плечи ℓ помно-

жить на водоизмещение D. Если – наоборот, то восстанавливающие моменты нужно

делить на водоизмещение.

или - или

max

в = f (θ)

или

ℓ = φ (θ).

0 10 20 30 40 50 60 70 80

Углы крена , град

Рис. 4.2.1.1. Диаграмма статической остойчивости при крене судна на правый борт.

Во всех официальных документах ДСО принято представлять в масштабе

плеч, однако более глубокое понимание вопросов, связанных с ДСО, достигает-

ся при использовании масштаба восстанавливающих моментов. Каждому углу

крена на ДСО соответствует конкретное значение М

в или ℓ, а так как эти зна-

чения соответствуют конкретному z

g, выраженному через D, то для каждого во-

доизмещения нужно строить отдельную ДСО.

Из изложенного выше следует, что количественными измерителями остойчи-

вости на больших углах крена являются либо восстанавливающий момент либо

плечо восстанавливающего момента.

3.5. НОРМИРОВАНИЕ ПЛАВУЧЕСТИ

Одним из важнейших вопросов безопасной эксплуатации судна является вопрос о

нормировании загрузки, т.е. до какой предельной степени разрешается загружать

судно. Для этого, необходимо сначала ознакомиться с понятием запаса плавучести.

Запасом плавучести называется объем судна (V

зап), заключенный между главной

палубой (палубой, до которой доведены главные водонепроницаемые переборки) и

плоскостью действующей ватерлинии. Объем судна, лежащий ниже главной палубы,

считается водонепроницаемым. Иначе говоря, запас плавучести – это надводный

водонепроницаемый объем судна (см. рис.3.5.1.а). Если на загруженное судно при-

нимать некий избыточный груз Р

изб (это может быть лед при обледенении или вода,

попавшая через пробоину), то запас плавучести будет уменьшаться или, более пра-

вильно, расходоваться. При Р

изб = γVзап запас плавучести будет полностью израс-

ходован, т.е. палуба окажется на уровне моря и судно утонет. Учитывая,что удель-

ный вес пресной воды γ = 1,0 т/м³, можно утверждать, что запас плавучести в м³

численно равен такому избыточному весу груза в тоннах, который топит судно.

Значит, чем больше запас плавучести, тем больше избыточного груза может при-

нять судно до своего затопления и, следовательно, больше времени будет тонуть

судно и появится больше возможностей для его спасения.

Таким образом , чтобы предупредить возможность затопления судна от перегруз-

ки, должен оставаться некоторый минимально допустимый запас плавучести, кото-

рому должна соответствовать предельная загрузка судна. Иначе говоря, загрузка суд-

на может вестись только до такого предела, пока на судне не останется

минимально допустимый запас плавучести. Минимально допустимый запас плаву-

чести для конкретного судна определяется проектантом на основании минимально

допустимого относительного запаса плавучести, который представляет собой про-

центное отношение запаса плавучести к подводному объему. Это отношение разное

для различных типов судов и зависит от степени опасности условий

а) б)

Угол заката ДСО

ℓ,(м)

в,(тм)

- Мв

Максимум ДСО

Угол максимума ДСО

Mв(max)

θзак

Fразр

Вид на борт в районе миделя

Ризб = γVзап

пт

Vзап

Fразр

в тро-

пиках

летом

зимой

зимой в

Северной

Атлантике

тп

ЗСА

Разрешенный надводный

бо

Рис. 3.5.1. Запас плавучести, грузовая марка и гребенка

эксплуатации или степени ответственности судна по условиям безопасности. Так

например, арктический ледокол имеет относительный запас плавучести порядка

80%, а портовый ледокол – 10%; пассажирское судно – 80%, а транспортное – 30%.

Приведенные цифры получены на основании обобщения и анализа гибели от пере-

грузки многих десятков или сотен тысяч судов за многие столетия их эксплуатации.

Таким образом, в конечном счете, в основе назначения минимально допустимого

запаса плавучести и, отсюда, предельно допустимой загрузки лежит накопленный

человечеством опыт безопасной эксплуатации судов.

Неизбежно возникает вопрос о том, как оперативно измерять и контролировать

запас плавучести в процессе загрузки судна. Чисто технически сделать это трудно,

так как судно имеет сложную форму, внутренние помещения загромождены и дей-

ствующая ватерлиния изнутри не просматривается. Поэтому для нормирования пла-

вучести используется не минимально допустимый запас плавучести, а разрешенная,

т.е. минимально допустимая, высота надводного борта (F

разр), косвенно характери-

зующая запас плавучести (см. рис. 3.5.1.). Для возможности контроля этой высоты в

процессе загрузки на обоих бортах в районе миделя наносится специальный знак,

называемый грузовой маркой. Грузовая марка – это две горизонтальные короткие

черты (см. рис. 3.5.1.б). Верхняя черта проходит на уровне главной палубы, нижняя

– на расстоянии F

разр. Для того, чтобы сделать нижнюю черту более заметной, на

нее накладывают круг (круг Плимсоля). Предельная загрузка должна быть такой,

чтобы предельная ватерлиния касалась нижней черты, т.е. высота надводного

борта была не меньше F

разр. Нижняя черта с кругом называется знаком грузовой

марки. Нередко приходится слышать некорректное выражение – “осадка судна или

водоизмещение по грузовую марку”. Принципиальная ошибка здесь состоит в том,

что осадка или водоизмещение характеризуют подводный объем судна, а грузовая

марка - надводный водонепроницаемый объем судна. Часто путают понятие “грузо-

вая марка” (две черты) с понятием “знак грузовой марки” (одна нижняя черта). F

разр

рассчитывается по специальным “Правилам о грузовой марке”, установленным меж-

дународной конвенцией. Борьба за введение грузовой марки, т. е. за ограничение

предельной загрузки судна, велась в конце 19 века в течение десятков лет с целью

сломить сопротивление судовладельцев, стремившихся за счет перегрузки судна (за-

частую, в ущерб безопасности судна) получать дополнительные прибыли от фрахта.

С точки зрения безопасности судно может эксплуатироваться в разных условиях,

поэтому, в качестве компромисса и компенсации потери части прибыли судовла-

дельцами, рядом с грузовой маркой устанавливается на транспортных судах неогра-

ниченного района плавания гребенка, которая дифференцированно устанавливает

разр, в зависимости от сезона и района плавания судна (см. рис. 3.5.1 б). Чем безо-

паснее условия эксплуатации, тем меньшей может быть разрешена высота надводно-

го борта и, за счет этого, увеличена предельная загрузка судна и, соответствено, по-

лучена дополнительная прибыль. Знак грузовой марки (нижняя черта) соответствует

летним условиям эксплутации в средних широтах. Наиболее тяжелые условия и, со-

ответственно, наибольшая F

разр имеет место зимой в Северной Атлантике.

кривую. Отсутствие фиксированного метацентра аннулирует все понятия начальной

остойчивости – метацентр, метацентрическая высота, метацентрический радиус – и

делает непригодными для дальнейшего использования основные формулы начальной

остойчивости.

Остается важным вопрос о том, как зависит остойчивость, т.е. восстанавливающий

момент М

в , от угла крена θ. Ранее (в разделе 4.1) эта зависимость определялась ме-

тацентрической формулой остойчивости (9), для вывода которой необходимо было

сначала найти связь плеча остойчивости ℓ с углом крена θ в виде ℓ = h*Sin θ, а затем

подставить в М

в = D* ℓ. Значит, для нахождения искомой зависимости Мв = f (θ)

необходимо предварительно найти зависимость ℓ = φ (θ).

Эта зависимость выглядит так (вывод опускаем):

ℓ = x*Cos θ + y*Sin θ - (z

g -zc) *Sin θ

(23)

Параметры, входящие в нее, см. на рис. 4.2.1.

Рис. 4.2.2. Полная диаграмма статической остойчивости на оба борта.

ℓ

(

)

θ°

Крен на левый борт

ℓ

(

)