Байдак Ю.В., Слободниченко Б.И. Электрооборудование технологических комплексов. Конспект лекций
Подождите немного. Документ загружается.

4. по расплавлению или изменению цвета некоторых веществ.
При измерении спиртовым или ртутным термометром, для уменьшения
погрешности следует обеспечить хорошее его прилегание к месту детали с
помощью асбеста, бумаги и защитить его от оттока, либо притока тепла со
стороны. При наличии переменного магнитного поля пользоваться ртутным
термометром нельзя (из-за действия вихревых токов). Недостатком метода
является большая погрешность и сложность при измерении в
труднодоступных точках.
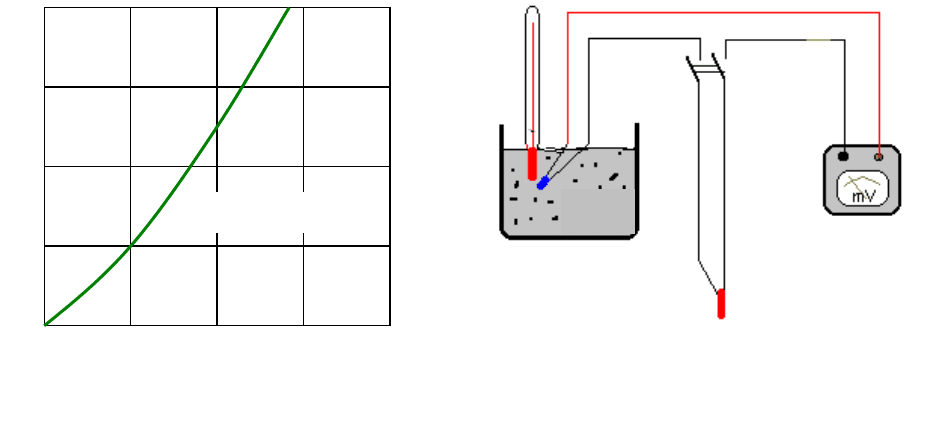
Термоэлектрический термометр представляет собой термопару вместе
с измерительным прибором - гальванометром. Известно, что если нагреть
место соединения (спай) двух проводников выполненных из разных
металлов, то на свободных - холодных концах проводников возникнет
разность потенциалов – термоэлектродвижущая сила е
т
, значение которой
растёт с ростом разности температур места спая и свободных концов.
Величина термо-ЭДС нелинейная функция температуры. Поэтому
термопары после изготовления градуируют, т.е. опытным путём снимают
зависимость е
т
=f(τ) по которой определяют превышение температуры τ =
f(е
т
). При этом показания прибора при градуировке зависит от сопротивления
самого прибора, поэтому градуировка и измерение температуры
производится одним и тем же прибором – гальванометром. Наибольшую е
т
31
Дифференциальное включение
контрольной термопары
θ
хол
θ
гор
τ = θ
хол
- θ
гор
Зависимость термо-ЭДС пары от
температуры горячего спая, θ
о
= 0
τ,
о
С
600400200
6
4
2
0
медь - платина
e
т
мВ

имеют термопары медь-константан - 0,04 мВ/К. Следует иметь в виду, что
термопара измеряет не температуру того места, в котором заложен ее спай, а
превышение этой температуры над температурой ее противоположного
холодного конца.
Среди используемых термоэлектрических термометров (термопар)
можно выделить ТПП – платинородий-платиновые, ТПР – платинородий-
платинородиевые, ТВР – вольфрам-рениевые, ТХК – хромель-копелиевые,
ТХА – хромель-алюмелиевые, которые нашли широкое применение в
технике в силу малых размеров и возможности размещения в
труднодоступных местах.
В методе определения температуры по изменению величины
сопротивления измеряется электрическое сопротивление обмотки в
холодном состоянии R
хол
и, затем, в нагретом R
гор
состоянии, либо по ходу
нагрева, и, по изменению величины сопротивления, определяется средняя
температура обмотки. Далее, по известным выражениям
)]15(1[
15
ХОЛХОЛ
RR
и
)]15(1[
15
ГОРГОР
RR
и их соотношению
15
1
15
1
)15(1
)15(1
ХОЛ
ГОР
ХОЛ
ГОР
ГОР
ХОЛ
R
R
,
32
Обозначение
термопары
Диапазон измеряемых
температур,
о
С
Инерционность Область применения
ТПП
От –20 до +1300 До 40 с В лабораторных
испытательных установках
ТПР
От –300 до +1700 От 5 с до 3 мин То же
ТВР
От –60 до + 1950 От 1,5с до 3мин Для измерения высоких температур
в печах с водородом или аргоном
ТХА
От –50 до +1000 От 8с до 3,5мин
Общепромышленное
применение
ТХК
От –50 до 600 От 3с до 3,5мин То же

подставив в которое коэффициент удельного сопротивления или
проводимости для медных обмоток
1
004,0
K
, либо
)(250
1
0
cK
,
получим
235
235
ХОЛ
ГОР
ГОР
ХОЛ
R
R
. Откуда
235)235(
ХОЛ
ГОР
ХОЛ
ГОР
R
R
о
С.
В качестве сопротивлений для определения температуры в жидких и
газообразных средах преимущественно используются проволочные
терморезисторы марки ТСП – платиновые для измерения температур в
диапазоне (–200 + 650
о
С) или ТСМ – медные - (+50+ 150
о
С).
Определение температуры тела по расплавлению или изменению цвета
плавких веществ используется в быстропротекающих процессах, в которых
инерционность измерительных устройств и приборов имеет решающее
значение. Эти вещества выполняют в роль индикаторов и позволяют только
установить, была ли температура выше или ниже какого-то определенного
значения.
2.11 Косвенный метод определения установившегося превышения
температуры
Во многих случаях опытное определение установившегося превышения
температуры
y
электрического аппарата требует длительного времени (10-
20часов), что создаёт большие неудобства, либо неприемлемо. В этом случае
пользуются частично снятой характеристикой нагрева
)(tf
, которая
является экспоненциальной функцией. Метод основан на том, что график
зависимости
)(
dt
d
f
представляет собой прямую линию.
Если выполнить дифференцирование уравнения нагрева
τ = P·(1-e
-t/T
) / ( k
т
·S)+ τ
o
·e
-t/T
,
по времени, то получим
T
t
y
e
Tdt
d
, где τ
у
= P / ( k
т
·S).
33
Но, как следует из общего уравнения нагрева, при нулевых начальных
условиях
0
0
, уравнение можно записать в виде
y
T
t
y
e
.
Осуществив его подстановку в предыдущее выражение, получим
y
dt
d
T
, либо:
dt
d
T
y
.
Полученное выражение является уравнением прямой линии, в котором
линейно зависит от скорости нагрева
dt
d
. Если в уравнении
0
, то это
возможно при
Tdt
d
y
, если
y
dt
d
;0
, Таким образом, можно по участку
кривой нагрева определить значения установившегося превышения
температуры τ
у
и постоянной времени нагрева
ОХЛT
S
cm
T
.
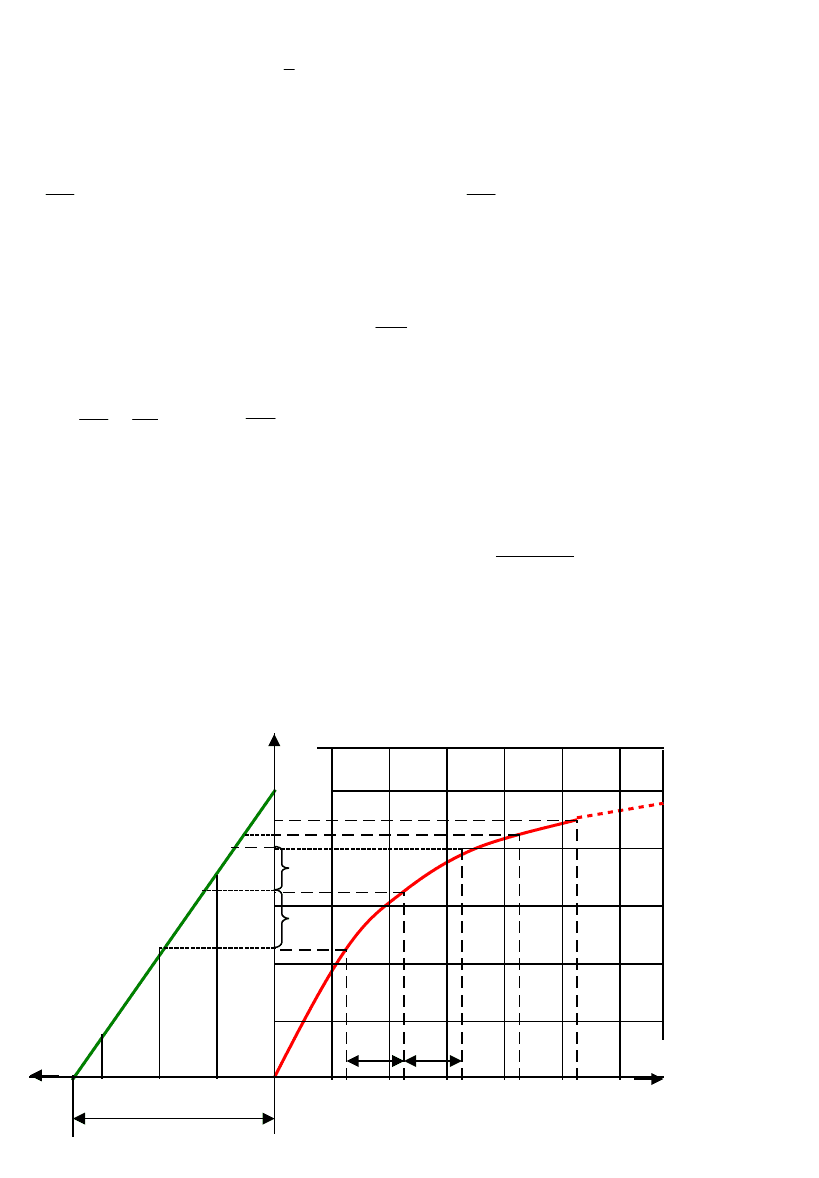
Графическое определение установившегося превышения температуры
в ЭА приведено на рисунке.
Вопросы для самоконтроля
2.1. Назовите основные источники тепла в электрических аппаратах.
34
80
∆t∆t
∆τ
2
∆τ
1
20
m
t
∆τ
3
/∆t
m
t
∆τ
2
/∆t
m
t
∆τ
1
/∆t
∆τ/∆t
τ
у
τ
100
60
20
t
60403020100
τ
у
/T
30
40
50
2.2. Напишите в дифференциальной и интегральной формах закон
Джоуля-Ленца.
2.3. Какое явление называют явлением поверхностного эффекта?
2.4. Какое явление называют эффектом близости?
2.5. Изобразите качественно кривую распределения плотности
переменного тока по сечению прямоугольной шины.
2.6. Изобразите кривую распределения плотности переменного тока по
сечениям параллельных прямоугольных шин, расположенных узкими
сторонами близко друг к другу (токи в шинах направлены либо в разные
стороны, либо в одну сторону).
2.7. От какого параметра зависит коэффициент поверхностного
эффекта для проводников из немагнитного материала?
2.8. Как зависит коэффициент поверхностного эффекта от удельного
сопротивления материала проводника?
2.9. Чем объясняется нагрев нетоковедущих ферромагнитных частей
электрических аппаратов, находящихся вблизи проводника с переменным
током?
2.10. Перечислите меры борьбы с нагревом нетоковедущих частей,
находящихся вблизи проводников с переменным током.
2.11. Зависит ли коэффициент поверхностного эффекта от геометрии
проводника?
2.12.В каком случае коэффициент поверхностного эффекта больше: в
случае неферромагнитного или же в случае ферромагнитного проводника
при прочих равных условиях?
2.13. Как зависит коэффициент поверхностного эффекта от частоты
переменного тока?
2.14. Напишите выражение для потерь в проводниках при переменном
токе с учётом эффекта близости и поверхностного эффекта.
2.15. Для какой цели применяют трубчатые проводники в случае
переменного тока?
35
2.16. Для какой цели применяют продольные разрезы трубчатых
проводников?
2.17. Напишите закон Стефана-Больцмана для теплопередачи
излучением.
2.18. Напишите формулу Ньютона для теплоотдачи с поверхности
нагретых тел.
2.19. Объясните физический смысл коэффициента теплоотдачи с
поверхности нагретого тела.
2.20. Почему коэффициент теплоотдачи в воде больше, чем в масле?
Почему коэффициент теплоотдачи в воде больше, чем в воздухе?
2.21. Напишите уравнение кривой нагрева и охлаждения тела.
2.22. Дайте основное определение постоянной времени нагрева.
2.23. Примерно, какой долю от установившейся температуры
приобретёт тело через время нагрева, равное постоянной времени нагрева?
2.24. Определите постоянную времени нагрева при помощи
касательной к кривой нагрева, проведенной через начало координат.
2.25. Что такое адиабатический процесс нагрева?
2.26. Практически в течение какого времени, в долях от постоянной
времени нагрева, процесс можно считать адиабатическим?
2.27. Какое из двух геометрически подобных тел, большое или
маленькое, достигнет быстрее установившейся температуры?
2.28. Дайте понятие установившегося превышения температуры тела.
Практически через сколько постоянных времени нагрева достигается
установившаяся температура тела?
2.29. Дайте определение коэффициента перегрузки по мощности и току
при повторно-кратковременном режиме нагрева.
2.30. Определите понятие относительной продолжительности
включения.
2.31. Что такое фиктивное время нагрева при кратковременном режиме
нагрева?
36
2.32. Дайте понятие термической стойкости электрического аппарата.
2.33. Напишите в общем виде критериальное уравнение для случая
теплоотдачи с поверхности нагретого тела.
2.34. Како вид имеет график изменения температуры в толще плоской
стенки при передаче через неё тепла теплопроводностью для случаев, если
отсутствует источник тепла в стенке и, если в стенке имеются равномерно
распределённые источники тепла?
2.35. Напишите выражение аналога закона Ома для случая
теплопроводности и объясните смысл входящих в него величин.
2.36. Какими видами теплопередачи распространяется тепло в твёрдых
телах, жидкостях, газах и в вакууме?
2.37. Изобразите ход кривой распределения температуры в плоской,
изолированной с двух сторон стенке с внутренними источниками тепла в
ней.
2.38. Укажите источники тепла в катушке постоянного и переменного
тока с ферромагнитным сердечником.
2.39. В каком случае наиболее нагретый слой в катушке находится на
её внутренней поверхности?
2.40. в каком случае наиболее нагретый слой в катушке находится на её
наружной поверхности?
2.12 Простейшие методы расчёта нагрева и охлаждения ЭА и их
частей
В данном параграфе приведены рекомендации к расчету простейших задач по
определению мощности источников теплоты: джоулева тепла, потерь от
поверхностного эффекта, эффекта близости, тепловыделения в ферромагнитных
нетоковедущих частях, находящихся в переменном магнитном поле, а также задач
по расчёту теплоотдачи с поверхностей нагретых тел, с учётом наиболее
распространённых в ЭА поверхностей охлаждения.
37
Количество теплоты, выделяемое в неоднородном проводнике объёмом V за
отрезок времени ∆t=t
1
-t
2
, при неравномерном распределении плотности тока j в нём, равно
t
2
Q = ∫ ∫j
2
ρ
о
(1+αθ)dVdt ,
t
1
V
где ρ
о,
α – удельное сопротивление, Ω·м, и температурный коэффициент сопротивления, 1/
о
С, материала проводника при 0
о
С соответственно; θ – температура проводника,
о
С.
Мощность источника теплоты для однородных проводников при переменном токе
P
~
= к
п
к
б
I
2
ρ
о
(1+αθ)ℓ/S,
где к
п
и к
б
– соответственно коэффициенты поверхностного эффекта и эффекта близости,
которые для неферромагнитных проводников определяют по графикам; ℓ и S – длина, м, и
площадь поперечного сечения, м
2
, проводника с током I, А, соответственно.
Для проводника состоящего из ферромагнитного материала
к
п
= S/(Πz
a
),
где S, Π – площадь,м
2
, и периметр поперечного сечения, м, проводника соответственно; z
a
– глубина проникновения электромагнитной волны, м
________
z
a
=
√ρ/(ωμ
о
μ
r
) , если H>Hμ
rмакс
;
________
z
a
=
√2ρ/(ωμ
о
μ
r
) , если H≤Hμ
rмакс,
38
√f/R
100
к
п
1,8
1,6
1,4
1,2
1,0
600400200
0,2 0,12
0,06
0,04
0,02
δ
D
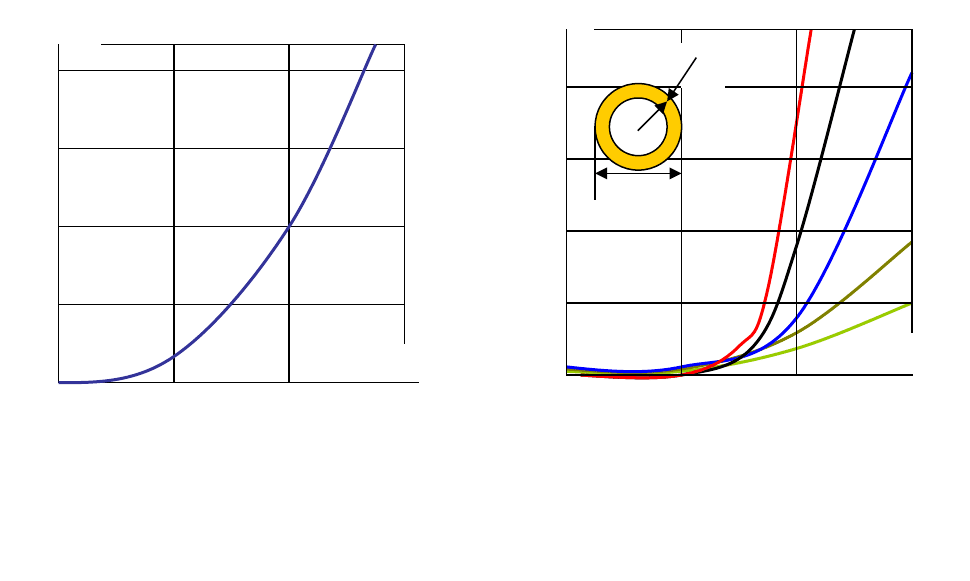
Коэффициент поверхностного эффекта
для полых трубчатых проводников из
немагнитного материала с различными
соотношениями δ/D от √f/R
100
300
√f/R
100
200100
к
п
1,8
1,6
1,4
1,2
1,0
Зависимость Кп для сплошных
круглых немагнитных проводников от
параметра √f/R
100
, где f частота
переменного тока, R
100
активное
сопротивление постоянному току
проводника длиной l=100 м.
где ω – угловая частота переменного поля; μ
о
= 4π10
-7
Гн/м; μ
r
– относительная магнитная
проницаемость; H – напряженность магнитного поля, А/м; Hμ
rмакс,
- амплитуда первой
гармоники напряженности магнитного поля, А/м, соответствующая максимуму μ
r
на
кривой намагничивания материала.
Для приближенных расчётов мощность источников теплоты в ферромагнитных
проводниках при переменном токе можно считать равной
Р = (2,9…3,25)10
-4
(I/Π)
5/3
S√f,
где S и Π боковая поверхность, м
2
, и периметр поперечного сечения, м, проводника; f, -
частота переменного тока, Гц.
Мощность источников теплоты в ферромагнитных нетоковедущих частях,
находящихся в переменном магнитном поле, определяют:
- для замкнутого сплошного магнитопровода, на котором надета катушка,
P=(2,9…3,25)10
-4
(I·w/ℓ
ср
)
5/3
S√f,
где I·w – намагничивающая сила катушки,А; ℓ
ср
–длин средней магнитной силовой линии,
м; S – боковая поверхность охлаждения магнитопровода, м
2
.
Для практических расчетов рекомендуется принимать среднее значение мощности:
- для замкнутого шихтованного магнитопровода
P= p
c
G;
- для ферромагнитного кольца, охватывающего проводник с током I,
P=(2,9…3,25)10
-4
(I/ℓ
ср
)
5/3
S√f,
где ℓ
ср
– длина средней магнитной силовой линии, м; S – поверхность охлаждения
кольца, м
2
.
- для единицы длины ферромагнитной полосы (балки), расположенной
перпендикулярно проводнику с током I,
P=(I
2
ΠρCos
4
α)/(4z
a
π
2
d
2
),
где α – угол между вектором напряженности магнитного поля в одной точке и его
составляющей вдоль продольной оси полосы; Π – периметр поперечного сечения, м; ρ –
удельное сопротивление материала полосы, Ω·м; d – минимальное расстояние между
осями проводника с током и полосы, м.
Мощность источников теплоты в электрической изоляции, находящейся в
переменном электрическом поле,
P=ωCU
2
tgδ,
где ω – угловая частота переменного поля; С – электрическая ёмкость изолятора, Ф; U –
напряжение, приложенное к изолятору, В; tgδ – тангенс угла диэлектрических потерь.
39

Количество теплоты, которое отводится с поверхности ЭА в окружающую среду в
стационарном режиме, по формуле Ньютона
P=k
т
S(θ-θ
о
),
где k
т
–коэффициент теплоотдачи, Вт/(м
2
К); S – охлаждающая поверхность, м
2
; θ и θ
о
–
температуры поверхности и окружающей среды,
о
С.
Для приближенных расчетов коэффициент теплоотдачи определяют по
эмпирическим формулам:
- для окрашенной краской прямоугольной шины с размерами поперечного
сечения 120х10 мм, находящейся в спокойном воздухе, большая сторона
сечения которой расположена вертикально
k
т
= 9,2(1+0,9·10
-
2·τ),
где τ= θ-θ
о
перепад температур;
- для горизонтальных цилиндрических проводников, окрашенных краской и
расположенных горизонтально в спокойном воздухе,
k
т
= 10k
1
(1+k
2
·10
-
2·τ)
где k
1
и
определяют по таблице
- для круглой трубы диаметром d, внутри которой протекает вода со скоростью υ,
k
т
= 1710·υ
0,8
d
0,2
(22-τ)
0,4
,
- для цилиндрических катушек в случае, когда охлаждающая поверхность
10
-4
<S<10
-2
м
2
,
k
т
=2,1[1+0,005(θ-θ
о
)] /
3
√S,
- для цилиндрических катушек, у которых 10
-2
<S<0,5
м
2
,
k
т
=3,6[1+0,005(θ-θ
о
)] /
5
√S.
Пример 1. Определить коэффициент поверхностного эффекта алюминиевого
шинопровода, нагретого протекающим по нему переменным током промышленной
частоты до температуры θ =95
о
С для следующих случаев: а) шинопровод круглый d = 80
мм; б) шинопровод трубчатый с наружным диаметром d
нар
=80 мм и с внутренним
диаметром d
вн
= 50 мм; в) шинопровод трубчатый с d
нар
= 80 мм, d
вн
= 74 мм.
Решение. Коэффициент поверхностного эффекта определим по графикам, Для этого
вычислим параметр его сечения √f/R
100
. Для условия (а) задачи
R
100
=ρ
о
(1+αθ)·ℓ/S
пр
=2,62·10
-8
(1+0,0042·95)·100/(3.14·40
2
·10
-6
) = 7,3·10
-4
Ω;
40
0,68
1,02
0,75
1,08
0,88
1,11
1,14
2,24
1,7
4,5
2008040100,3
k
2,
о
С
k
1
, Вт/(м
2
К)
Диаметр проводника, мм
