Basdevant J.-L., Rich J., Spiro M. Fundamentals in Nuclear Physics: From Nuclear Structure to Cosmology

Подождите немного. Документ загружается.

60 1. Basic concepts in nuclear physics

is surrounded by a non-spherically symmetric electron cloud. This eﬀect

adds to the normal hyperﬁne splitting due to the interaction of the nuclear

magnetic moment with the magnetic ﬁeld created by atomic electrons. It

should be noted that the quadrupole eﬀect allows one to determine the sign

of the quadrupole moment. It turns out that the most deformed nuclei have

Q>0 (prolate deformation).

electron

deformed

nucleus

cloud

Fig. 1.18. The energy of a non-spherical nucleus surrounded by a non-spherical

distribution of electrons depends on the orientation of the nuclear symmetry axis

with respect to the electron cloud. The ﬁgure shows a prolate nucleus at the center of

a donut-shaped electron cloud in the xy-plane. The nuclear symmetry axis makes an

angle θ with respect to the z axis. Orientations with θ ∼ 0 have a larger electrostatic

energy than those with θ ∼ π/2 since the mean nucleon-electron distance is greatest

for θ = 0. Quantum-mechanically, the symmetry axis cannot be taken to point in

a ﬁxed direction. For a rigid object of deﬁnite J

and J

, the amplitude for the

symmetry axis to make and angle θ with the z axis is given by the appropriate

spherical harmonic, Y

(θ, φ) where l = J and m = J

. The spherical harmonics

with m = l are maximized at θ = π/2 while those with m = 0 are maximized at

θ = 0. We can therefore expect that, in general, the electrostatic energy of a prolate

nucleus is lowest for the largest |J

| states. The magnitude of the eﬀect is estimated

in Exercise 1.12. Note that there can be no quadrupole hyperﬁne splitting for nuclei

with J =0orJ =1/2 since in these two cases there is only one possible value of

Muonic atoms

The small hyperﬁne eﬀects due to nuclear deformation become dominant

eﬀects in muonic atoms.Themuonµ, which was discovered in 1937 and

whose existence is still somewhat of a mystery, is basically a heavy electron.

It is elementary, or point-like in the same way as the electron. It has the same

electricchargeandthesamespin,butitis200timesheavier,m

= 206.8m

It is unstable, decaying into an electron and two neutrinos:

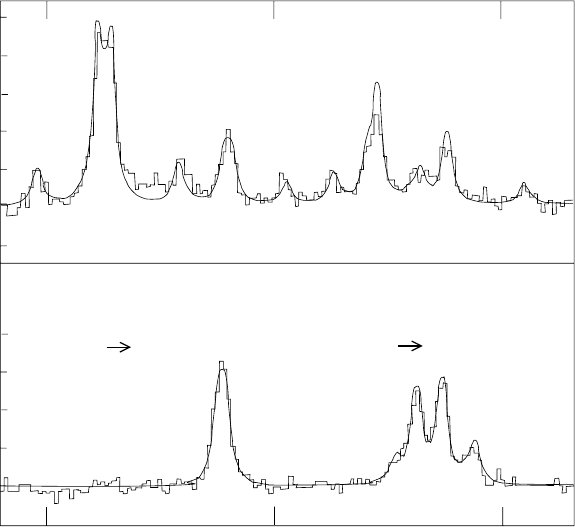
1.8 Deformed nuclei 61

−

→ e

−

(1.150)

with a lifetime of τ =2× 10

−6

s. The muon-neutrino ν

is associated with

the muon in the same way that the electron neutrino ν

is associated with

the electron.

4.4

4.5

4.6

(MeV)

x−ra

200

400

600

counts

400

153

151

1/2

3/2

Fig. 1.19. Transition lines of the 2p

1/2

and 2p

3/2

states to the 2s

1/2

state in muonic

europium (Z = 63) [26]. As detailed in Exercise 1.14, the energy of all transition

photons are near the expected value ∼ (3/8)(Zα)

.Inthe

151

Eu spectrum,

one sees the expected ﬁne-structure splitting between the 2p

1/2

and 2p

3/2

states of

∼ (Zα)

and the hyperﬁne splitting of the 2p

3/2

level due mostly to the slight

deformation of the

151

Eu nucleus. On the other hand, the

153

Eu nucleus is strongly

deformed, resulting in a very complicated spectrum. The complication is due to the

fact that the eigenstates of the muonic atom are are mixtures of the ground state

of the

153

Eu nucleus and its excited states.

In particle accelerators, one produces muons, one can slow then down in

matter and have them captured by atoms, inside which they form hydrogen-

like atoms.

62 1. Basic concepts in nuclear physics

In a multi-electron atom, the muon is not constrained by the Pauli prin-

ciple. The µ thus cascades down to the lowest energy orbitals where it is in

the direct vicinity of the nucleus at a distance a

∼ ¯h

/Z m

, 200 times

smaller than the corresponding Bohr radius of internal electrons. It therefore

forms a hydrogen-like atom of charge Z around the nucleus, oblivious to the

presence of the other electrons at larger distances from the nucleus.

The muon lifetime is considerably larger than the total time ≈ 10

−14

sec

for it to cascade to the inner orbitals and even larger compared to the atomic

time scale ¯h

≈ 10

−19

s (the orbital period of the muon). The µ can

therefore be considered stable.

For heavy nuclei, the Bohr radius of a muonic atom is of the same order

as the nuclear radius. In lead, for instance, Z = 82, of radius R ≈ 8.5 fm, the

Bohr radius is a

≈ 3.1fm. The µ therefore penetrates the nucleus, having a

90 % probability to be inside the nucleus in the ground state. Because of this,

the study of muonic atom spectra gives useful information on the structure of

nuclei, in particular on the charge (i.e. proton) distribution inside the nuclei.

In the case of a spherical nucleus, the potential is harmonic inside the

nucleus (assuming a uniform charge density) and Coulomb-like outside. The

deviation of the position of levels compared to the Coulomb case gives infor-

mation about the radial charge distribution. If the nucleus is non-spherical,

the states of the same l but diﬀerent m are split.

A spectacular example is given by the two isotopes

151

Eu and

153

Eu of

europium Z = 63, whose spectra are given on Fig. 1.19. The lighter isotope

is relatively spherical. Conversely, the spectrum of

153

Eu is much more com-

plex. In other words, if

151

Eu absorbs two neutrons (neutral particles and

do not aﬀect directly the Coulomb forces) the proton distribution completely

changes. Needless to say that this provides very useful information on nuclear

structure.

1.9 Bibliography

1. The Nuclear Many-Body Problem, P. Ring and P. Schuck, Springer Verlag

(1980).

2. Nuclear Forces D.M. Brink, Pergamon Press, Oxford (1965).

Exercises

1.1 Compare the mass of 1 mm

of nuclear matter and the mass of the Earth

(∼ 6 × 10

kg).

1.2 A commonly used quantity is the mass excess deﬁned as

Exercises for Chapter 1 63

∆ ≡ m(A, Z) − A × 1u . (1.151)

Derive an expression for ∆ in terms of the nuclear binding energy B(A, Z).

1.3 Figure 1.2 shows that

H has more tightly bound than

He. Why is it,

then, that

H β-decays to

He?

1.4 Calculate the recoil energy of

208

Pb in the c.m. decay

212

Po →

208

Pb+α.

(The masses of the nuclei can be calculated from the data in Appendix G.)

1.5 Consider the reaction γ +

C → 3

He. What is the threshold energy of

the reaction? If two α-particles have the same momentum in the c.m. system,

what fraction of the energy is carried by the third particle ?

1.6 The A = 40 isotopes of calcium (Z = 20), potassium (Z = 19) and argon

(Z = 18) have respective binding energies −332.65 MeV, −332.11 MeV and

−335.44 MeV. What β decays are allowed between these nuclei? Specify the

available energy Q in the ﬁnal state. What peculiarity appears?

1.7 In Sect. 1.2.3 we showed how the proton–deuteron mass ratio can be

determined accurately from the ratio of the masses the ionized deuterium

atom and a singly ionized hydrogen molecule. To place these two nuclei on

the atomic-mass-unit scale, we need the mass ratio of the deuteron and the

non-ionized

C atom (≡ 12 u). This ratio can be accurately determined from

the ratio of the masses of the singly-ionized

molecule and the doubly-

ionized

C atom. To do this, show that

12 u



+2m

m(12, 6) + 4m



1 − m

/6u

1+2m

/(3m

)



, (1.152)

where the ﬁrst bracketed term on the right is the aforementioned ratio. The

second bracketed factor diﬀers from unity only by small factors depending

on the ratio of electron and nuclear masses and are therefore second-order

corrections that need not be known as accurately as the ﬁrst term.

1.8 Verify (1.21).

1.9 Consider a quantum system of A pairwise interacting fermions with two-

body attractive interactions of the form V (r)=−g

/r. Using the uncertainty

relation

p

≥A

2/3

¯h

1/r

show that <E>/A−A

4/3

·g

m/8¯h

,and

See J.-L. Basdevant and J. Dalibard, Quantum mechanics, chapter 16, Springer-

Verlag, 2002.

64 1. Basic concepts in nuclear physics

r  2¯h

−1/3

/mg

. This is a usual cumulative eﬀect for attractive forces:

energies per particle increase and radii decrease as the number of particles

increases. The powers 4/3and−1/3 are speciﬁc to the Coulomb-type in-

teractions but one can verify that, for a harmonic potential, one obtains

|E/A|∼A

5/6

and for a spherical well, |E/A|∼A

2/3

. This shows that the

Pauli principle alone cannot lead to saturation of nuclear forces.

1.10 Write the momentum- and energy-conservation equations for reaction

(1.102). Show that if the initial neutron and nucleus are at rest, the ﬁnal-state

photons takes nearly all the released energy, Q.

1.11 Write the momentum- and energy-conservation equations for reaction

(1.103). Show that in the limit where the initial particles are at rest, the

neutron takes most of the released energy, Q =17.58 MeV.

1.12 The energies associated with the magnetic-dipole and electric-quadru-

pole moments of nuclei contribute to the hyperﬁne structure of atoms and

molecules. The purpose of this exercise is to estimate the size of these energies

compared to atomic binding energies ∼ α

Nuclei interact with a magnetic ﬁeld via the Hamiltonian

H = −B · µ (1.153)

where µ is the nuclear magnetic moment

µ = g

ZeJ

, (1.154)

where J is the nuclear spin and and g

is of order unity. The energies of the

(2j + 1) states are

Ze|B|

m¯hm= −j, −(j − 1).....(j −1),j . (1.155)

Consider a nucleus surrounded by a non-spherically symmetric electron

cloud as in Fig. 1.18. Atomic electrons move at velocities ∼ αc with respect

to the nucleus. Argue that the magnetic ﬁeld seen by the nucleus is of order

|B|∼

αce

∼

¯h

, (1.156)

where a

=¯h/(αm

c) is the Bohr radius giving the typical nuclear–electron

distances. Show that this leads to a splitting of nuclear levels of order

∆E ∼ g

. (1.157)

This splitting is a factor α

) smaller than the binding energy and a

factor m

smaller than the ﬁne structure (spin orbit) splittings.

Exercises for Chapter 1 65

The energy associated with the nuclear electric-quadrupole moment can

be estimated by calculating the electrostatic energy of the conﬁguration in

Fig. 1.18 as a function of the angle θ.(θ ∼ 0 corresponds to |J

|∼0and

θ ∼ π/2 corresponds to |J

|∼J.) Argue that energy diﬀerence between θ =0

and θ = π/2 for a highly deformed nucleus is of order

∆E ∼ Z

(1.158)

where R is the length of the longest nuclear dimension. Compare ∆E with

that due the magnetic moment (1.157). What energy splitting would you

expect for a slightly deformed nucleus? How would the splitting be diﬀerent

for an oblate nucleus?

1.13 Consider a proton-rich material that is placed in a magnetic ﬁeld

of |B| = 1 T. What is the energy diﬀerence between a proton with its spin

aligned with B and one with its spin anti-aligned? Supposing thermal equi-

librium at kT = 300 K, what is the relative number of proton spins aligned

and anti-aligned with the magnetic ﬁeld. What frequency oscillating ﬁeld can

induce transitions from the more populated state to the less populated one?

The absorption of energy by such a ﬁeld tuned to the correct frequency

is called nuclear magnetic resonance (NMR). It is the basis of magnetic res-

onance imaging (MRI) where the number of protons in a sample is deduced

from the absorbed power. In medical applications, why is this technique

mostly useful for deducing the amount of hydrogen and not other elements?

Consider two protons in a molecule separated by 10

−10

m. Compare the

external magnetic ﬁeld of 1 T with the magnetic ﬁeld seen by a proton due to

the spin of its neighbor. The extra magnetic ﬁeld shifts the resonant frequency

making it sensitive to the molecular structure of the sample.

1.14 Estimate the transition energies of the

151

Eu atom shown in Fig. 1.19

by supposing that the muon forms a hydrogen-like atom.

1.15 The osmium mass spectrum on the right of Fig. 1.3 is due to osmium

extracted from a mineral containing 0.32% rhenium and 0.00161% osmium

[10]. Using the half-life and isotopic abundance of

187

Re from Table 5.2 derive

the age of the mineral. Discuss what is meant by this “age”.

1.16 The data of Fig. 1.4 gave the ﬁrst precise measurement of the atomic

mass of

Mn. Taking the binding energies of

Cr and

Fe as known (from

Appendix G), use the data to estimate the binding energy of

Mn. What

precision can be obtained with this method?

66 1. Basic concepts in nuclear physics

1.17 The purpose of this exercise is to estimate the energy spectrum of the

protons recoiling from collisions with

Ni nuclei (Fig. 1.7). Since the proton

is much lighter than

Ni, we can anticipate that most of the kinetic energy

will be taken by the proton. Under this assumption, use energy conservation

to show that the energy of the ﬁnal state proton is E



= E

−∆E where ∆E

is the energy of the produced excited state of

Ni relative to the ground state.

Use momentum conservation to estimate the momentum and kinetic energy of

the recoiling

Ni for protons recoiling at 60

from the beam direction. Finally,

re-estimate the proton energy by imposing energy conservation taking into

account the recoil of the

Ni.

2. Nuclear models and stability

The aim of this chapter is to understand how certain combinations of N neu-

trons and Z protons form bound states and to understand the masses, spins

and parities of those states. The known (N, Z) combinations are shown in Fig.

2.1. The great majority of nuclear species contain excess neutrons or protons

and are therefore β-unstable. Many heavy nuclei decay by α-particle emis-

sion or by other forms of spontaneous ﬁssion into lighter elements. Another

aim of this chapter is to understand why certain nuclei are stable against

these decays and what determines the dominant decay modes of unstable nu-

clei. Finally, forbidden combinations of (N,Z) are those outside the lines in

Fig. 2.1 marked “last proton/neutron unbound.” Such nuclei rapidly (within

∼ 10

−20

s) shed neutrons or protons until they reach a bound conﬁguration.

The problem of calculating the energies, spins and parities of nuclei is one

of the most diﬃcult problems of theoretical physics. To the extent that nuclei

can be considered as bound states of nucleons (rather than of quarks and glu-

ons), one can start with empirically established two-nucleon potentials (Fig.

1.12) and then, in principle, calculate the eigenstates and energies of many

nucleon systems. In practice, the problem is intractable because the number

of nucleons in a nucleus with A>3ismuchtoolargetoperformadirect

calculation but is too small to use the techniques of statistical mechanics. We

also note that it is sometimes suggested that intrinsic three-body forces are

necessary to explain the details of nuclear binding.

However, if we put together all the empirical information we have learned,

it is possible to construct eﬃcient phenomenological models for nuclear struc-

ture. This chapter provides an introduction to the characteristics and physical

content to the simplest models. This will lead us to a fairly good explanation

of nuclear binding energies and to a general view of the stability of nuclear

structures.

Much can be understood about nuclei by supposing that, inside the nu-

cleus, individual nucleons move in a potential well deﬁned by the mean in-

teraction with the other nucleons. We therefore start in Sect. 2.1 with a brief

discussion of the mean potential model and derive some important conclusions

about the relative binding energies of diﬀerent isobars. To complement the

mean potential model, in Sect. 2.2 we will introduce the liquid-drop model

that treats the nucleus as a semi-classical liquid object. When combined with

68 2. Nuclear models and stability

Z=20

Z=28 Z=28

Z=50 Z=50

Z=82 Z=82

N=20

N=28N=28

N=50N=50

N=82N=82

N=126N=126

Z=20

nucleon emission

spontaneous fission

last neutron unbound

half−life> 10

proton

unbound

last

decay

A=100

A=200

Fig. 2.1. The nuclei. The black squares are long-lived nuclei present on Earth.

Combinations of (N, Z) that lie outside the lines marked “last proton/neutron

unbound” are predicted to be unbound by the semi-empirical mass formula (2.13).

Most other nuclei β-decay or α-decay to long-lived nuclei.

2.1 Mean potential model 69

certain conclusions based on the mean potential model, this will allow us to

derive Bethe and Weizs¨acker’s semi-empirical mass formula that gives the

binding energy as a function of the neutron number N and proton number

Z. In Sect. 2.3 we will come back to the mean potential model in the form

of the Fermi-gas model. This model will allow us to calculate some of the

parameters in the Bethe–Weizs¨acker formula.

In Sect. 2.4 we will further modify the mean-ﬁeld theory so as to explain

the observed nuclear shell structure that lead to certain nuclei with “magic

numbers” of neutrons or protons to have especially large binding energies.

Armed with our understanding of nuclear binding, in Sections 2.5 and 2.6

we will identify those nuclei that are observed to be radioactive either via β-

decay or α-decay. Finally, in Sect. 2.8, we will discuss attempts to synthesize

new metastable nuclei.

2.1 Mean potential model

The mean potential model relies on the observation that, to good approxima-

tion,individualnucleonsbehaveinsidethenucleusasindependent particles

placed in a mean potential (or mean ﬁeld) due to the other nucleons.

In order to obtain a qualitative description of this mean potential V (r),

we write it as the sum of potentials v(r − r



) between a nucleon at r and a

nucleon at r



V (r)=



v(r − r



)ρ(r



)dr



. (2.1)

In this equation, the nuclear density ρ(r



), is proportional to the probability

per unit volume to ﬁnd a nucleus in the vicinity of r



. It is precisely that

function which we represented on Fig. 1.1 in the case of protons.

We now recall what we know about v and ρ. The strong nuclear interaction

v(r − r



) is attractive and short range. It falls to zero rapidly at distances

larger than ∼ 2 fm, while the typical diameter on a nucleus is “much” bigger,

of the order of 6 fm for a light nucleus such as oxygen and of 14 fm for lead.

In order to simplify the expression, let us approximate the potential v by a

delta function (i.e. a point-like interaction)

v(r − r



) ∼−v

δ(r − r



) . (2.2)

The constant v

can be taken as a free parameter but we would expect that

the integral of this potential be the same as that of the original two-nucleon

potential (Table 3.3):



rv(r) ∼ 200 MeV fm

, (2.3)

wherewehaveusedthevaluesfromTable3.3.Themeanpotentialisthen

simply