Basdevant J.-L., Rich J., Spiro M. Fundamentals in Nuclear Physics: From Nuclear Structure to Cosmology

Подождите немного. Документ загружается.

30 1. Basic concepts in nuclear physics

0.6

0.8

1.0

1.2

1.4

1.6

200

400

600

counts

E (MeV)

(MeV)

22+

30+

40+

50+

60+

30+

40+

10+

20+

prolate

oblate

prolate superdeformed

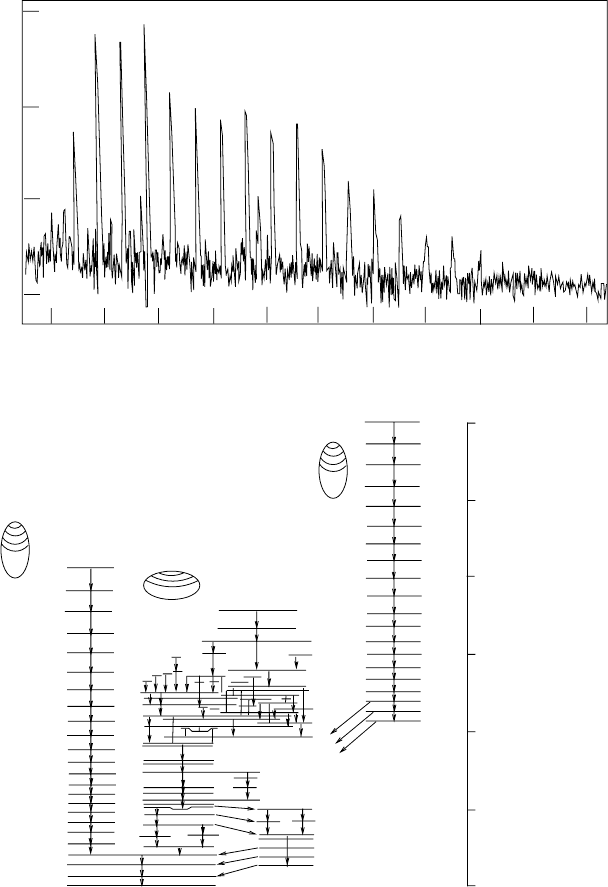
Fig. 1.9. Excited states of

152

Dy. The bottom panel [21] shows the spectrum of

states, including (on the left) the ground state rotation band for a prolate nucleus

and (on the right) a super-deformed band extending from J

∼ 22

to 60

.Nu-

clei in states of a rotation band generally cascade rapidly down the band, giving

coincident photons that are evenly spaced in energy. The top panel [22] shows the

“picket fence” spectrum of photons produced in a cascade of the super-deformed

band.

1.4 Nuclear forces and interactions 31

from ﬁrst principles. In fact Coulomb’s law (or more generally the equations of

electromagnetism) determines the interactions between electrons and nuclei.

Spin corrections and relativistic eﬀects can be calculated perturbatively to

very good accuracy because of the smallness of the ﬁne structure constant

α = e

/4π

¯hc ∼ 1/137. Together with the Pauli principle which leads to the

shell structure of electron orbitals, these facts imply that one can calculate

numerically spectra of complex atoms despite the diﬃculties of the many-

body problem.

Unfortunately, none of this holds in nuclear physics. Forces between nu-

cleons are neither simple nor fully understood. One of the reasons for this

is that the interactions between nucleons are “residuals” of the fundamental

interactions between quarks inside the nucleons. In that sense, nuclear in-

teractions are similar to Van der Waals forces between atoms or molecules,

which are also residual or “screened” Coulomb interactions. For these rea-

sons, forces between nucleons are described by semi-phenomenological forms,

e.g. (1.56), which are only partly deduced from fundamental principles.

Reversing the order of inference, physicists could have derived the form

of Coulomb’s law from the spectrum of bound states of the hydrogen atom.

This is not possible in nuclear physics because there is only one two-nucleon

bound state, the deuteron. In the next subsection, we will ﬁnd that there is

much to be learned from this fact but it will not be suﬃcient to derive the

nucleon–nucleon potential in all its detail. To do this, we will need to attack

the more diﬃcult problem of nucleon–nucleon scattering. This will be done

in Chap. 3. When we do this, we will be confronted with the other major

diﬃculty of nuclear forces: the coupling constants are large so perturbative

treatments do not apply as systematically as in atomic physics.

1.4.1 The deuteron

There is only one A = 2 nucleus, the deuteron, and it has no excited states.

Its binding energy, quantum numbers, and magnetic moments are

B(2, 1) = 2.225 MeV J

=0.857µ

. (1.42)

Note that B(2, 1) is quite small compared to typical nuclear binding energies,

8 MeV per nucleon.

We also note that to good approximation µ

= µ

+µ

.Thissuggeststhe

the magnetic moment comes only from the spins of the constituents, implying

that the nucleons are in a state of vanishing orbital angular momentum,

l = 0. In fact, this turns out only to be a good ﬁrst approximation since the

deuteron is slightly deformed, possessing a small quadrupole moment. This

requires that the wavefunction have a small admixture of l = 2. Both l =0

and l = 2 are consistent with the parity of the deuteron since for two-nucleon

states, the parity is −1

Since the deuteron has spin-1 and is (mostly) in an l = 0 state, the spins

of the nucleons must be aligned, i.e. the total spin, s

tot

= s

+ s

,must

32 1. Basic concepts in nuclear physics

take on the quantum number s = 1. The other possibility is s = 0. Since the

deuteron is the only bound state, we conclude

n p (s = 1) bound n p (s = 0) unbound .

We conclude that the neutron–proton potential is spin-dependent.

What about the neutron–neutron and proton–proton potentials and the

fact that there are no bound states for these two systems? If the strong inter-

actions do not distinguish between neutrons and protons, the non-existence

of a s = 0 neutron–proton state is consistent with the non-existence of the

analogous pp and nn states:

n n (s = 0) unbound p p (s = 0) unbound ,

i.e. all nucleon–nucleon s =0,l = 0 states are unbound. On the other hand,

the non-existence of pp and nn s =1,l = 0 states is explained by the

Pauli principle. This principle requires that the total wavefunction of pairs

of identical fermions be antisymmetric. Loosely speaking, this is equivalent

to saying that when two identical fermions are at the same place (l = 0),

their spins must be anti-aligned. Thus, the l =0,s = 1 proton–proton and

neutron–neutron states are forbidden.

We make the important conclusion that the existence of a n p bound state

andthenon-existenceofnnandppboundstatesisconsistentwiththestrong

force not distinguishing between neutrons and protons but only if the force

is spin-dependent.

Theexistenceofans = 1 state and non-existence of s = 0 states would

naively suggest that the nucleon–nucleon force is attractive for s = 1 and

repulsive for s = 0. This is incorrect. In fact the nucleon–nucleon force is

attractive in both cases. For s = 1 it is suﬃciently attractive to produce a

bound state while for s = 0 it is not quite attractive enough.

We can understand how this comes about by considering the 3-dimensional

square well potential shown in Fig. 1.10:

V (r)=−V

r<R V(r)=0 r>R. (1.43)

While it is hardly a realistic representation of the nucleon–nucleon potential,

its ﬁnite range, R,anditsdepthV

can be chosen to correspond more or less

to the range and depth of the real potential. In fact, since for the moment

we only want to reproduce the deuteron binding energy and radius, we have

just enough parameters to do the job.

The bound states are found by solving the Schr¨odinger eigenvalue equa-

tion



−¯h

∇

+ V (r)



ψ(r)=Eψ(r) , (1.44)

where m is the reduced mass m ∼ m

/2 ∼ m

/2. The l = 0 solutions depend

only on r, so we set ψ(r)=u(r)/r and ﬁnd a simpler equation

1.4 Nuclear forces and interactions 33

V(r)=0

r=R

κ r)

V(r)=−V

|u|

V(r)

u(r) = sin kr

u(r) = exp(−

Fig. 1.10. A square-well potential and the square of the wavefunction ψ(r)=

u(r)/r. The depth and width of the well are chosen to reproduce the binding energy

and radius of the deuteron. Note that the wavefunction extends far beyond the

eﬀective range of the s = 1 nucleon–nucleon potential.



−¯h

+ V (r)



u(r)=Eu(r) . (1.45)

The solutions for E<0 oscillate for r<R

u(r<R) ∝ A sin kr + B cos(kr) k(E)=



2m(V

+ E)

¯h

, (1.46)

and are exponentials for r>R

u(r>R) ∝ C exp(−κr)+D exp(κr) κ(E)=

√

−2mE

¯h

. (1.47)

We set B = 0 to prevent ψ from diverging at the origin and D =0tomake

the wavefunction normalizable. Requiring continuity at r = R of u(r)and



(r) we ﬁnd the condition that determines the allowed values of E

k(E)cotk(E)R = −κ(E) . (1.48)

We note that for r → 0, the function on the left, k cot kr, is positive and

remains so until kr = π/2. Since the quantity on the left is negative the

requirement for at least one bound state is that there exist an energy E<0

such that

k(E)R>π/2 , (1.49)

34 1. Basic concepts in nuclear physics

i.e. that we can ﬁt at least 1/4 of a wave inside the well. Since k(E) <k(E =

0) the condition is

√

2mV

¯h

>π/2 , (1.50)

i.e.

¯h

8mc

= 109 MeV fm

. (1.51)

The existence of a single s = 1 state and the non-existence of s = 0 states

can be understood by supposing that the eﬀective values of V

are respec-

tively slightly greater than or slightly less than 109 MeV fm

. The deuteron

binding energy is correctly predicted if

(s = 1) = 139.6MeVfm

. (1.52)

This can be veriﬁed by substituting it into (1.48) along with the energy

E = −2.225 MeV. Data from neutron–proton scattering discussed in Chap.

3 shows that the s = 0 states just miss being bound

(s =0) ∼ 93.5MeVfm

. (1.53)

Including scattering data, Sect. 3.6, we can determine both V

and R:

s =1: V

=46.7MeV R =1.73 fm . (1.54)

The wavefunction in shown in Fig. 1.10. The fact that B(2, 1) is small results

causes the wavefunction to extend far beyond the eﬀective range R of the

potential and explains the anomalously large value of the deuteron radius

(Table 1.1).

The scattering data discussed in Sect. 3.6 allow one to estimate the values

of V

and R for s = 0 (Table 3.3). One ﬁnds for the proton–neutron system

s =0: V

=12.5MeV R =2.79 fm . (1.55)

This potential is quite diﬀerent from the s = 1 potential.

In summary, the strong interactions have a strength and range that places

them precisely at the boundary between the the interactions that have no

bound states (e.g. the weak interactions) and those that have many bound

states (e.g. the electromagnetic interactions). The phenomenological implica-

tions are of a cosmological scale since the fabrication of heavy elements from

nucleons must start with the production of the one 2-nucleon bound state.

As we will see in Chaps. 8 and 9, if there were no 2-nucleon bound states the

fabrication of multi-nucleon nuclei would be extremely diﬃcult. On the other

hand, the existence of many 2-nucleon states would make it considerably

simpler. The actual situation is that heavy elements can be slowly formed,

leaving, for the time being, a large reserve of protons to serve as fuel in stars.

1.4 Nuclear forces and interactions 35

1.4.2 The Yukawa potential and its generalizations

We want to consider more realistic potentials than the simple potential (1.43).

This is necessary to completely describe the results of nucleon–nucleon scat-

tering (Chap. 3) and to understand the saturation phenomenon on nuclear

binding. The subject of nucleon–nucleon potentials is very complex and we

will give only a qualitative discussion. Our basic guidelines are as follow:

• Protons and neutrons are spin 1/2 fermions, and therefore obey the Pauli

principle. We have already seen in the previous subsection how this restricts

the number of 2-nucleon states.

• Nuclear forces are attractive and strong, since binding energies are roughly

a10

times the corresponding atomic energies. They are however short

range forces : a few fm. The combination of strength and short range makes

2-nucleon systems only marginally bound but creates a rich spectrum of

many-nucleon states.

• They are “charge independent.” Nuclear forces are blind to the electric

charge of nucleons. If one were to “turn oﬀ” Coulomb interactions, the

nuclear proton–proton potential would be the same as the neutron–neutron

potential. A simple example is given by the binding energies of isobars such

as tritium and helium 3 : B(

H) = 8.492 MeV >B(

He) = 7.728 MeV. If

the diﬀerence ∆B =0.764 MeV is attributed to the Coulomb interaction

between the two protons in

He, ∆B = e

< 1/r

>/4π

, one obtains

a very reasonable value for the mean radius of the system : R ≈ 2 fm (this

can be calculated or measured by other means). We shall come back to this

question in a more quantitative way when we discuss isospin.

• Nuclear forces saturate. As we have already mentioned, this results in the

volumes and binding energies of nuclei being additive and, in ﬁrst approx-

imation, proportional to the mass number A.Thisisaremarkablefact

since it is reminiscent of a classical property and not normally present in

quantum systems. It appears as if each nucleon interacts with a given ﬁxed

number of neighbors, whatever the nucleus.

The theoretical explanation of the saturation of nuclear forces is subtle.

The physical ingredients are the short range attractive potential (r ∼ 1fm),

a hard core repulsive force at smaller distances r<0.5 fm, and the Pauli

principle. Being the result of these three distinct features, there is no simple

explanation for saturation. It is simple to verify that the Pauli principle alone

cannot suﬃce, and that any power law force does not lead to saturation

(Exercise 1.9).

Many properties of nuclear forces can, be explained quantitatively by the

potential proposed by Yukawa in 1939:

V (r)=g

¯hc

exp(−r/r

) . (1.56)

The factor ¯hc is present so that the coupling constant g is dimensionless. As

we will see in the next section, forces between particles are due, in quantum

36 1. Basic concepts in nuclear physics

ﬁeld theory, to the quantum exchange of virtual particles.Theranger

of a

force is the Compton wavelength ¯h/mc of the exchanged particle of mass m.

Yukawa noticed that the range of nuclear forces r

 1.4 fm, corresponds to

the exchange of a particle of mass  140 MeV. This is how he predicted the

existence of the π meson. The discovery of that particle in cosmic rays was a

decisive step forward in the understanding of nuclear forces.

When applied to a two-nucleon system, the potential (1.56) is reduced

by a factor of (m

/2m

)

∼ 10

−2

because of spin-parity considerations. A

dimensionless coupling constant of g  14.5 explains the contribution of the

π meson to the nucleon–nucleon force.

It is necessary to add other exchanged particles to generate a realistic

potential. In fact, the general form of nucleon–nucleon strong interactions

can be written as a linear superposition of Yukawa potentials :

V (r)=



¯hc

exp(−µ

r) (1.57)

where the sum is over a discrete or continuous set of exchanged particles with

masses given by µ

= m

c/¯h.

However, we need some more elements to explain saturation and prevent

a nuclear “pile-up” where all nucleons collapse to an object of the size of the

order of the range of the strong interactions.

First, one must add a strong repulsive shorter range potential, called a

“hard core”interaction. This potential is of the form (1.56) with a negative

coupling constant g and a range r

 0.3 fm. The physical origin of the

repulsive core is not entirely understood but it certainly includes the eﬀect of

the Pauli principle that discourages placing the constituent quarks of nucleons

near each other.

Second, spin eﬀects and relativistic eﬀects must be taken into account.

One writes the potential as the sum of central potentials with spin-dependent

coeﬃcients:

V = V

(r)+Ω

SO2

(r) , (1.58)

where V

is a pure central potential and the other terms are spin dependent.

The most important is the tensor potential V

with

Ω

=[3(σ

· r/r)(σ

· r/r) − σ

· σ

] (1.59)

where σ

and σ

are the Pauli spin matrices for the two nucleon spins. Figure

1.11 shows how this term has the important eﬀect of inducing a correlation

between the position and spin of the two nucleons. This results in a permanent

quadrupole moment for the deuteron. It is also the dominant force in binding

the deuteron. However, it averages to zero for multi-nucleon systems where

it plays a minor role.

The last two terms in (1.58) are spin-orbit interactions:

¯hΩ

=(σ

+ σ

) · L (1.60)

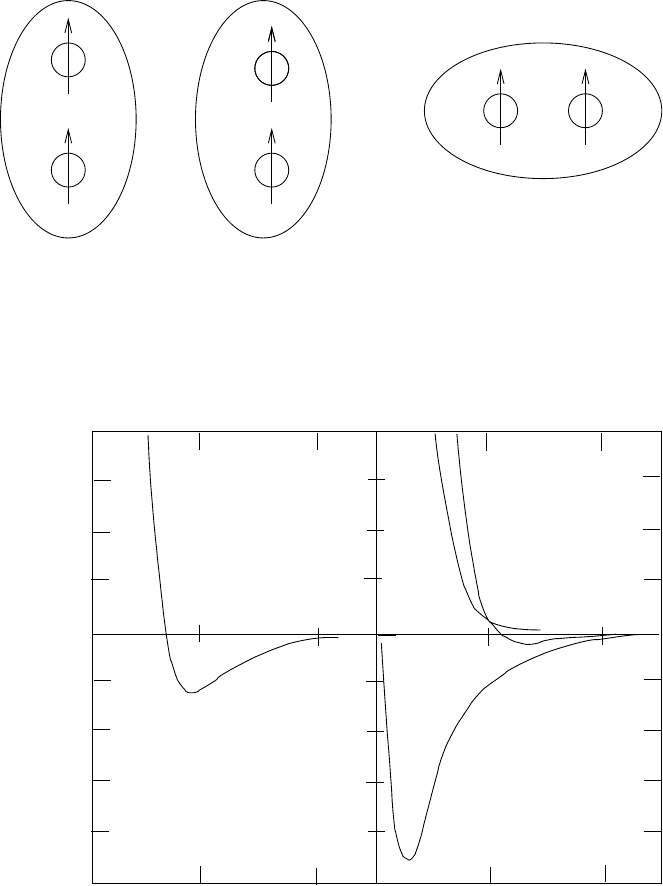
1.4 Nuclear forces and interactions 37

Fig. 1.11. The tensor potential for the s = 1 state (1.59) makes the conﬁguration

on the right (σ ·r = 0) have a diﬀerent potential energy than the two conﬁgurations

on the left (σ · r = 0). This results in the permanent quadrupole moment of the

deuteron.

p−p n−n p−n

p−n

−200

−150

−100

−50

100

150

V(r) (MeV)

r (fm)

121

r (fm)

S=1

Fig. 1.12. The most important contributions to the nucleon–nucleon potentials in

the s = 0 state (left) and the s = 1 state (right) (the so-called Paris potential).

The two central potentials V

depend only on the relative separations. The tensor

potential V

is of the form (1.59) is responsible for the deuteron binding and for

its quadrupole moment. The spin-orbit potential is V

38 1. Basic concepts in nuclear physics

¯h

Ω

SO2

=(σ

· L)(σ

· L)+(σ

· L)(σ

· L) (1.61)

where L is the orbital angular momentum operator for the nucleon pair.

Figure 1.12 shows the most important contributions to the nucleon–

nucleon potential [23]. For spin-anti-aligned nucleons (s = 0), only the central

potential contributes.

Finally, we note that to correctly take into account the charge indepen-

dence of nuclear forces the formalism of isospin (Sect. 1.7) must be used.

1.4.3 Origin of the Yukawa potential

The form (1.56), which is derived from quantum ﬁeld theory, can be under-

stood quite simply. Consider a de Broglie wave

ψ =exp



− i(Et − p.r)/¯h



. (1.62)

The Schr¨odinger equation in vacuum is obtained by using E = p

/2m and

then taking the Laplacian and the time derivative. Assume now that we use

the relativistic relation between energy and momentum :

= p

+ m

(this is how Louis de Broglie proceeded initially). By taking second-order

derivatives of (1.62) both in time and in space variables we obtain the Klein—

Gordon equation :

∂

∂t

−∇

ψ + µ

ψ = 0 (1.63)

wherewehavesetµ = mc/¯h. Originally, this equation was found by

Schr¨odinger. He abandoned it because it did not lead to the correct rela-

tivistic corrections for the levels of the hydrogen atom.

It was rediscovered

later on by Klein and Gordon.

Forgetting about the exact meaning of ψ in this context, (1.63) is the

propagation equation for a relativistic free particle of mass m.Inthecase

m = 0, i.e., the photon, we recover the propagation equation for the electro-

magnetic potentials :

∂

∂t

−∇

ψ =0 . (1.64)

The classical electrostatic potential produced by a point charge is obtained

as a static, isotropic, time-independent solution to this equation with a source

term added to represent a point-like charge at the origin, i.e.,

∇

V (r)=−



δ(r) , (1.65)

Schr¨odinger did not have in mind spin and magnetic spin-orbit corrections. These

eﬀects are accounted for by the Dirac equation, the relativistic wave equation

for a spin 1/2 particle

1.4 Nuclear forces and interactions 39

whose solution is

V (r)=

4π

. (1.66)

Similarly, by looking for static, isotropic solutions of the Klein–Gordon

equation 1.63 with a point-like source at the origin :

∇

V (r) − µ

(r)=−

g(¯hc)

4π

δ(r) , (1.67)

one can readily check that the Yukawa potential (1.56)

V (r)=g(¯hc/r) exp(−µr) , (1.68)

satisﬁes this equation. The solution V (r)=g(¯hc/r) exp(+µr) is discarded

since it diverges at inﬁnity.

1.4.4 From forces to interactions

We have emphasized that, in quantum ﬁeld theory, forces between particles

are described by the exchange of virtual particles. The interactions can be

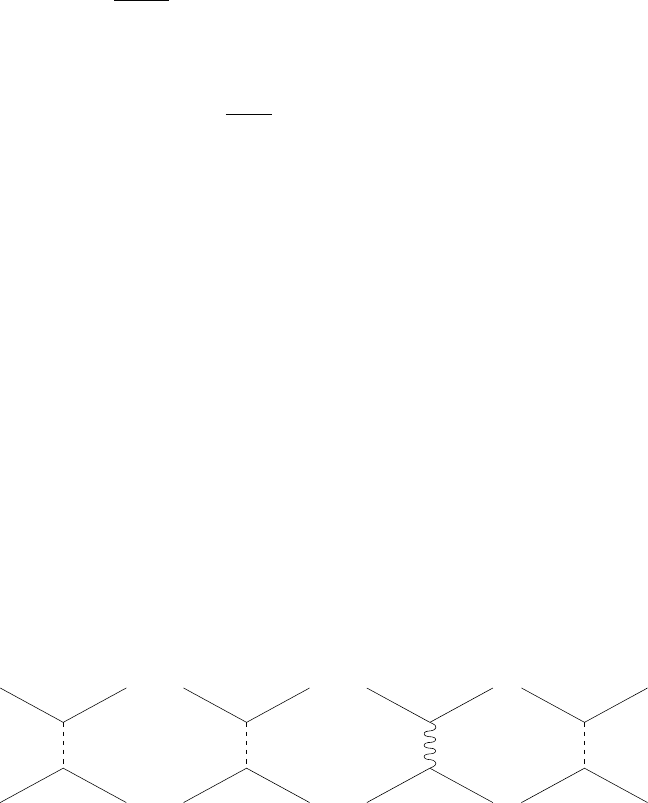
described by (Feynman) “diagrams” like those shown in Fig. 1.13. Each dia-

gram corresponds to a scattering amplitude that can be calculated according

to the rules of quantum ﬁeld theory. As we will see in Chap. 3, the eﬀective

potential is Fourier transform of the amplitude.

In quantum electrodynamics, the exchange of massless photons leads to

the Coulomb potential. The exchange of massive particles leads to Yukawa-

like potentials. One example is the exchange of pions as shown in the ﬁrst

two diagrams in Fig. 1.13. These diagrams contribute to the nucleon–nucleon

potential of Fig. 1.12 and lead to the binding of nucleons and to nucleon–

nucleon scattering.

N’ N’

NNNN

’

+−

Fig. 1.13. Diagrams contributing to the nucleon–nucleon interaction due to the

exchange of a pion, a photon and a Z

. In these diagrams N and N



represent either

a proton or a neutron. The two ﬁrst diagrams with the exchange of a neutral or

charged pion generates the long-range part of the nucleon–nucleon potential. The

photon exchange diagram generates the Coulomb interaction between protons and

the magnetic interaction between any nucleons. The diagram with Z exchange is

negligible for the nucleon–nucleon interactions but dominates for neutrino-neutron

scattering since the neutrino has no strong interactions.