Basdevant J.-L., Rich J., Spiro M. Fundamentals in Nuclear Physics: From Nuclear Structure to Cosmology

Подождите немного. Документ загружается.

40 1. Basic concepts in nuclear physics

WWW

ν e

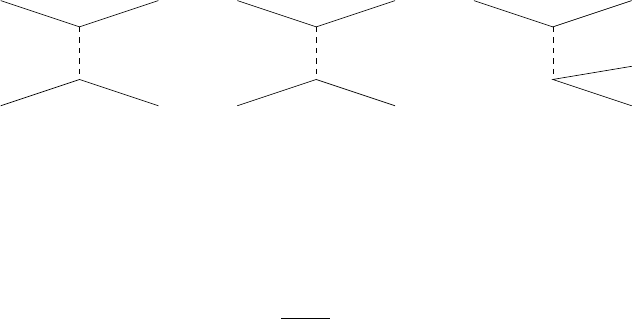
Fig. 1.14. Some diagrams with the exchange of a W. The two diagrams on the

left contribute to inelastic neutrino scattering. The diagram on the right leads to

neutron decay.

Other massive particles can be exchanged between particles, for example

the Z

boson

=91.188 GeV

¯hc

=2.11 × 10

−3

fm . (1.69)

This particle is the mediator of the neutral current sector of the weak in-

teractions as illustrated in the fourth diagram of Fig. 1.13. It thus leads to

a Yukawa-like potential between particles of the form (1.56). Compared to

pion exchange, the Yukawa potential has a range about 10

−3

times smaller.

The eﬀective coupling is also much smaller being of order

∼ α. (1.70)

To compare with the strong interactions, we estimate an eﬀective value of

by taking R ∼ 2 × 10

−3

fm and V

∼ α¯hc/R:

∼ 3 × 10

−3

MeV fm

, (1.71)

i.e. about 5 orders of magnitude smaller than that of the strong interactions

(1.52) and (1.53). We conclude that Z

can play no role in nucleon–nucleon

binding or scattering.

On the other hand, Z

exchange plays the essential role in neutrino–

nucleon elastic scattering. This is because the neutrino has only weak inter-

actions.

The use of particle exchange to describe potentials obviously has direct

applications in bound states and elastic scattering. If one includes the pos-

sibility of the exchange of charged particles, we can also describe inelastic

reactions, some of which are shown in Fig. 1.14. These diagrams show pro-

cesses where the particle exchanged is the charged partner of the Z

boson,

the W

=80.42 GeV . (1.72)

This particle mediates the so-called charged-current weak interactions. They

play the essential cosmological role of changing neutrons into protons and vice

versa. They thus play an essential role in the cosmological and astrophysical

synthesis of heavy elements. On Earth, they are mostly seen in neutrino

1.5 Nuclear reactions and decays 41

scattering and β-decay as illustrated in Fig. 1.14 and discussed further in the

next section.

Table 1.3 summarizes the interactions important in nuclear physics and

their exchanged particles. The weak and electromagnetic interactions are

fundamental interactions that will be discussed in more detail in Chap. 4.

The ordinary strong interactions that lead to binding of nucleons in nu-

clei are “eﬀective” in the sense that, as previously emphasized, they are the

screened residuals due to the fundamental chromodynamic interactions be-

tween quarks.

Table 1.3. The interactions involving elementary particles. The strong interac-

tions are considered to be screened quantum chromodynamic interactions.

interaction examples of reactions exchanged particle

weak neutral current νn → νnZ

weak charged current νn → e

−

electromagnetic ep → ep γ

strong np → np π and other hadrons

chromodynamic quark–quark scattering gluons

1.5 Nuclear reactions and decays

Nuclear species can be transformed in a multitude of nuclear reactions. In

nuclear reactions involving only strong and electromagnetic interactions, the

number of protons and the number of neutrons are conserved separately. An

important example is neutron absorption followed by photon emission, the

so-called “ (n, γ) ” reaction:

n(A, Z) → γ (A + 1, Z) i.e. (A, Z) (n, γ)(A+1, Z) . (1.73)

The second form is a standard way of denoting the reaction. Other reactions

are “ (p, γ) ” reactions

p(A, Z) → γ (A + 1, Z + 1) i.e. (A, Z) (p, γ)(A+1, Z+1), (1.74)

“(n, p)” reactions

n(A, Z) → p(A, Z − 1) i.e. (A, Z) (n, p) (A, Z − 1) , (1.75)

and “(p, n)” reactions

p(A, Z) → n(A, Z + 1) i.e. (A, Z) (p, n) (A, Z+1). (1.76)

In all these reactions, the ﬁnal state nucleus may be produced in an excited

state so additional photons are produced in de-excitation.

42 1. Basic concepts in nuclear physics

Many nuclei can decay to lighter nuclei by redistributing the nucleons

among “daughter” nuclei. The most important are “α-decays” with the emis-

sion of a

He nucleus :

(A, Z) → (A − 4,Z − 2)

He , (1.77)

for instance

238

U →

234

He. The condition for a nucleus to be stable

against α-decay is

m(A, Z) <m(A − 2,Z − 2) + m(2, 2) . (1.78)

Alpha decay will be studied in more detail in Sect. 2.6.

α-decay is a special case of spontaneous ﬁssion into two lighter nuclei

with, perhaps, the emission of k neutrons, such as:

(A, Z) → (A



)(A



)+k n , (1.79)

with A



+ A



+ k = A and Z



+ Z



= Z. Such decays occur mostly for very

heavy nuclei. They will be studied in more detail in Chap. 6.

While the strong and electromagnetic interactions responsible for the

above reactions separately conserve the number of neutrons and the num-

ber of protons, neutrons and protons can be transformed into each other by

the weak interactions mentioned in the previous section. These interactions

are weak in the sense that the rates of reactions they induce are in general

much slower than those due to the electromagnetic or strong interactions.

Weak interactions will be studied in some detail in Chap. 4. Here, we note

that weak nuclear interactions are usually signaled by the participation of an

electron–neutrino, ν

. Two examples are electron capture by a proton and

neutrino capture by a neutron

−

p ↔ ν

n . (1.80)

We see that when the proton is transformed to a neutron or vice-versa, an

electron or positron is created or absorbed to conserve charge. Since all par-

ticles in these reactions have spin 1/2, the neutrino is necessary to conserve

angular momentum. All other possible weak interactions can be found by

moving particles from left to right and changing them to their antiparticles,

e.g.

¯ν

p ↔ e

n . (1.81)

Another possibility is spontaneous neutron decay

n → pe

−

. (1.82)

Thisdecayisallowedbyenergyconservation,(m

− m

−m

=0.78 MeV,

and the free neutron has a mean-lifetime of

= 886.7 ± 1.9s. (1.83)

Of course, the fact that m

+ m

means that the corresponding decay

of free protons is forbidden

1.6 Conservation laws 43

p → ne

energy not conserved. (1.84)

Since the weak interactions can turn protons into neutrons and vice versa

while conserving the total number of nucleons, their most important role is

the decay of radioactive isobars via so-called β-decays:

(A, Z) → (A, Z +1)e

−

¯ν

(A, Z) → (A, Z − 1) e

. (1.85)

These two reactions are the nuclear equivalents of the two fundamental decays

(1.82) and (1.84). Another form of β-decay (or transmutation) is electron

capture

−

(A, Z) → (A, Z − 1) ν

, (1.86)

i.e. the nuclear equivalent of (1.80) This latter reaction is possible if the

nucleus is surrounded by atomic electrons but cannot happen in the case of

an isolated nucleus.

A nucleus is stable against the β-decays (1.85) if it is suﬃciently light

compared to its two neighboring isobars:

m(A, Z) <m(A, Z ± 1) + m

, (1.87)

where m(A, Z)standsforthemassofthe(A, Z) nucleus. The condition for

it to be stable against both β-decay and electron capture is slightly diﬀerent:

themassoftheatom containing A −Z neutrons, Z protons and Z electrons

must be smaller than the masses of its two neighboring isobars :

m(A, Z)+Zm

<m(A, Z ± 1) + (Z ± 1)m

. (1.88)

(In the above formula, we neglect the electronic binding energies which are

comparatively much smaller.) In general, for each value of the mass number A,

there exist only one or two stable isobars. The other nuclei are radioactive and

decay to the stable isobars by a series of β-decays and/or electron captures.

While the weak interactions do not conserve separately the number of

protons and the number of neutrons, they do (as do the strong and electro-

magnetic interactions) conserve electric charge and baryon number, i.e. the

total number of nucleons. Baryon number is conserved in nuclear reactions

but it is believed that very rare, as yet unobserved, reactions allow baryon

number non-conservation. On the other hand, electric charge conservation is

believed to be absolute.

1.6 Conservation laws

The investigation of the fundamental constituents of matter and their inter-

actions comes from the experimental and theoretical analysis of reactions.

These reactions can be scattering experiments with or without production of

particles, and decays of the unstable particles produced in these reactions.

44 1. Basic concepts in nuclear physics

Various fundamental conservation laws govern nuclear reactions. The laws

allow the identiﬁcation of particles, i.e. the determination of their masses,

spins, energies, momenta etc.

The most important laws are energy-momentum conservation, angular

momentum conservation and electric charge conservation. In nuclear physics,

other laws play an important role such as lepton number, baryon number and

isospin conservation.

In this book, we shall mainly make use of simple “selection rules” implied

by these conservation laws. In this section, we will ﬁrst discuss the experi-

mental and phenomenological consequences of the most important laws. We

will then show how the conservation laws are related to invariance proper-

ties of transition operators between initial and ﬁnal states, or, equivalently,

invariance laws of Hamiltonians of the systems under consideration.

1.6.1 Energy-momentum conservation

By far the most important conservation law is that for Energy-momentum.

For example, in nuclear β-decay

(A, Z) → (A, Z +1)e

−

(1.89)

we require

A,Z

= E

A,Z+1

+ E

, (1.90)

and

A,Z

= p

A,Z+1

+ p

. (1.91)

These two laws are only constraints. As discussed in later chapters, the way

that momentum and energy are distributed between the decay products de-

pends on the details of the interaction responsible for the reaction.

When one applies energy-momentum conservation, it is of course neces-

sary to take into account the masses of initial and ﬁnal particles by using the

relativistic expression for the energy

E =(p

+ m

)

1/2

(1.92)

for a free particle of mass m. The square root in this formula often makes cal-

culations very diﬃcult. However, in nuclear physics, nuclei and nucleons are

usually non-relativistic, v = pc

/E  c, and one can use the non-relativistic

approximation :

E =



+ m

 mc

+ p

/2m, (1.93)

i.e. the energy is the sum of the rest energy mc

and the non-relativistic

kinetic energy p

/2m. On the other hand, photons and neutrinos are rela-

tivistic:

E =



+ m

 pc + m

/2pc , (1.94)

1.6 Conservation laws 45

where the mass term m

/2pc can usually be neglected for neutrinos and

always for the massless photon E = pc.

The presence of non-relativistic and relativistic particles in a given re-

action results in the very useful fact that, viewed in the center-of-mass, the

momentum is shared democratically between all ﬁnal state particles whereas

the kinetic energy is carried mostly by the relativistic particles. This is most

easily seen in the decay of an excited nucleus:

(A, Z)

∗

→ (A, Z) γ . (1.95)

Energy conservation in the initial rest frame implies

∗

= mc

+ pc , (1.96)

where m

∗

and m are the masses of the excited and unexcited nuclei and

p is the common momentum of the ﬁnal nucleus and photon. (Momentum

conservation requires that these two momenta be equal.) It is clear that the

photon energy pc is much greater than the nuclear kinetic energy:

= pv/2  pc for v  c. (1.97)

Neglecting p

/2m in (1.96), we see that the photon energy is then to good

approximation proportional to the mass diﬀerence

pc ∼ (m

∗

− m)c

. (1.98)

Using this value for the momentum, we ﬁnd that the ratio between the nuclear

kinetic energy and the photon energy is

/2m

=(1/2)

∗

− m

. (1.99)

This is at most of order 10

−3

in transitions between nuclear states.

In more complicated reactions like three-body decays, one generally ﬁnds

that the momentum is evenly distributed on average among the ﬁnal-state

particles. Once again, this implies that the kinetic energy is taken by the

lightest particles.

In nuclear physics, one often mentions explicitly the energy balance in

writing reactions

A + B → a

+ a

+ Q (1.100)

where

Q =(Σm

− Σm

. (1.101)

If the reaction can take place when A and B are at rest, Q is the total kinetic

energy of the particles in the ﬁnal state. If Q is negative, the reaction is

endothermic and it can only take place if the energy in the center-of-mass is

above the energy threshold.

46 1. Basic concepts in nuclear physics

An important example in producing heavy elements is neutron capture

accompanied by the production of k photons:

n+(A, Z) → (A + 1, Z) + kγ + Q (1.102)

The fact that binding energies per nucleon are ∼ 8 MeV means that Q is

positive and of order 8 MeV (near the bottom of the stability valley). Since

the ﬁnal state photons are the only relativistic particles, we can expect that

they take all the energy,



∼ Q. A detailed calculation of the constraints

of energy-momentum conservation conﬁrms this (Exercise 1.10).

Of course, some reactions involve no relativistic particles, for example

dt → n

He + 17.58 MeV. (1.103)

We leave it to Exercise 1.11 to show that in the limit of low-center-of-mass

energy, the ﬁnal state neutron takes the majority of the 17.58 MeV.

1.6.2 Angular momentum and parity (non)conservation

Angular momentum conservations plays a diﬀerent role than that of energy-

momentum conservation. The latter can by veriﬁed to a useful precision in

individual events where the energies and momenta of ﬁnal-state particles can

be compared with those of the initial-state particles. This is because there is

a relatively well-deﬁned correspondence between momentum wavefunctions

(plane waves) and the classical tracks of particles that are actually observed,

i.e. a plane wave of wave vector k and angular frequency ω generates a de-

tector response that appears to be due to a classical particle of momentum

¯hk and energy E =¯hω.

On the other hand, the wavefunctions corresponding to a deﬁnite angular

momentum, correspond to certain angular dependence of the function about

the origin. This information is lost when an individual track going in a par-

ticular direction is measured. It can be recovered only by observing many

events and reconstructing the angular distribution.

The same consideration applies to parity which gives the behavior of a

wavefunction under reversal of all coordinates. Its conservation can only be

veriﬁed in the distribution of tracks. As it turns out, parity is not in fact

conserved in the weak interactions, as we will see in Chap. 4.

1.6.3 Additive quantum numbers

As we have already emphasized nuclear reactions may or may not respect

certain additive conservations laws. The most important is electric charge

conservation which is believed to be absolutely respected in all interactions.

The second most respectable conservation law is that of baryon number,

i.e. the total number of nucleons (neutrons and protons), minus the total

number of anti-nucleons (antiprotons and antineutrons). For instance, the

1.6 Conservation laws 47

reaction p d → pp γ conserves electric charge but not baryon number and is

therefore not observed. Conversely, the photo-disintegration of the deuteron,

γ d → p n, is allowed and observed. The baryon number conservation forbids

the decay of the proton, such as in the reaction p → e

γ. The present ex-

perimental limit on the proton lifetime, τ

> 10

yr shows that the baryon

number is conserved to very good accuracy.

Finally, we mention lepton number. The electron and the neutrinos are

called leptons.Thelepton number (more precisely the “electron lepton num-

ber”) L

is deﬁned as the diﬀerence between the total number of leptons

(electrons and neutrinos) and the total number of anti-leptons (anti-electrons

and antineutrinos)

≡ N (e

−

)+N(ν

) − N(e

) − N(¯ν

) , (1.104)

where N(e

−

) is the number of electrons, N(ν

) the number of neutrinos, etc.

is conserved in nuclear reactions involving electrons and neutrinos. In neu-

tron decay, for instance, n → p+e

−

+¯ν

,anantineutrino is produced together

with the electron in order to conserve the lepton number. This antineutrino

then can interact and produce a positron but not an electron:

¯ν

+p→ e

+ n but not ¯ν

+n→ e

−

+p. (1.105)

There exist two other types of charged leptons, the µ

= 105.66 MeV)

and the τ

= 1777.03 MeV). Each of these leptons is associated with its

own neutrino ν

and ν

both of which have very small masses. The “muon”

and “tauon” lepton numbers are deﬁned in the same way as the electron

lepton number:

≡ N (µ

−

)+N(ν

) − N(µ

) − N(¯ν

) , (1.106)

≡ N (τ

−

)+N(ν

) − N(τ

) − N(¯ν

) . (1.107)

They are both conserved separately. Since m

and m

are much larger than

characteristic nuclear energy scales (∼ 1 MeV), the µ and τ leptons have

fewer applications in nuclear physics than in particle physics.

In the same way as the strong nuclear interactions show that the neutron

is a neutral partner of the proton, weak interactions show that the ν

acts

as a neutral partner of the electron (and similarly for the ν

and µ,and

for the ν

and τ). We have been careful to use the words “acts as” because

it is now believed the separate conservation of electron, muon and tauon

lepton numbers is only an eﬀective conservation law. Recent experiments on

“neutrino oscillations” that are discussed in Chap. 4 indicate that the only

truly conserved number is the sum of the 3 lepton numbers:

L = L

+ L

. (1.108)

48 1. Basic concepts in nuclear physics

1.6.4 Quantum theory of conservation laws

A quantum system described by a state vector |ψ evolves with time in a way

governed by the Schr¨odinger equation and the system’s Hamiltonian operator

d|ψ(t)

= H |ψ(t) . (1.109)

It is interesting to see how the dynamics deﬁned by (1.109) conspires to

conserve a quantity associated with a time-independent operator A.One

answer is given by Ehrenfest’s theorem relating the time development of an

operator’s expectation value to the operator’s commutator with H:

ψ(t)|A|ψ(t) =

i¯h

ψ(t)|[A, H]|ψ(t) , (1.110)

which follows simply from (1.109) and its Hermitian conjugate. We see that

the expectation value is time independent if the operator commutes with H.

In nuclear physics, we are generally interested in transitions between

states and we would like to see how selection rules that constrain the transi-

tions are generated. Consider the transition amplitude of a system from an

initial state |i to a ﬁnal state |f , both eigenstates of a Hamiltonian H

due to a transition Hamiltonian H

. The total Hamiltonian of the system is

H = H

+ H

. In ﬁrst-order perturbation theory, i.e. in Born approximation,

for f = i, the amplitude γ

i→f

is proportional to the matrix element of H

between initial and ﬁnal states

i→f

∝f|H

|i . (1.111)

If A commutes with H

we can take the initial and ﬁnal states to be also

eigenstates of A with eigenvalues a

and a

, respectively,

A|i = a

|i ,A|f = a

|f . (1.112)

Since we suppose that A commutes with H

, we obtain

f|[A, H

]|i =(a

− a

)f|H

|i∝(a

− a

)γ

i→f

=0 . (1.113)

Therefore, either γ

i→f

= 0, i.e. the transition is forbidden, or, if it is not

forbidden, a

= a

.ThequantityA is conserved in any transition if A com-

mutes with the transition Hamiltonian. While we have shown this only in

Born approximation, the property can be extended to all orders of perturba-

tion theory.

The conservation of a quantity described by the operator A is equivalent

to the invariance of the Hamiltonian with respect to unitary transformations

deﬁned by the operator

D(α)=exp(iαA) , (1.114)

where α is an arbitrary real number. The operator D is unitary, i.e. D

D =1,

because A is Hermitian. The unitary transformation of states |ψ and of

operator B, associated with D is

1.6 Conservation laws 49

|ψ



 = D|ψ B



= DBD

. (1.115)

From the commutation relation [A, H]=0,wededuce

[D, H]=0 ⇒ H = DHD

†

. (1.116)

In other words, the Hamiltonian H is invariant under the unitary transfor-

mation D associated with the operator A.

We see that the conservation of A in the transitions induced by H is

a result of the invariance of H in the unitary transformation D.Tothis

symmetry property of the Hamiltonian there corresponds a conservation law

of the quantity A. The operator A is called the inﬁnitesimal generator of the

transformation D.

We also notice that equation (1.114) deﬁnes a group of transformations

D(α)D(β)=D(α + β). In the case of (1.114), the group is Abelian, or

commutative.

It is interesting to associate the various conservation laws of the previous

subsections with invariances. The Schr¨odinger equation (1.109) follows from

|ψ(t) = exp (iHt) |ψ(t =0) , (1.117)

if we assume that the Hamiltonian is time-independent. Equation (1.117) tells

us that the Hamiltonian is the generator of translations in time. Energy is

trivially conserved because the Hamiltonian commutes with itself so we can

conclude that energy conservation occurs for any time-invariant system. In

other words, it occurs in any isolated system.

Total momentum conservation comes from the invariance under transla-

tions in space. The inﬁnitesimal generator of the group of space translations

is the total momentum P .LetD(x

) be an element of this group

D(x

)=exp(ix

· P /¯h) , (1.118)

the translation invariance of the Hamiltonian can be written equivalently as

[H, D]=0⇔ [H, P ]=0.IfH is translation invariant, in a process leading

from an initial state of total momentum P

to a ﬁnal state of total momentum

, one has

[H, D]=0⇒ P

= P

. (1.119)

The conservation of the total angular momentum follows from the rotation

invariance of the transition Hamiltonian. Consider a rotation of an angle α

around an axis along the unit vector ˆu and set α = αˆu. The corresponding

unitary operator is

=exp(iα · J/¯h) . (1.120)

Consider an initial state which is an eigenstate of J

and J

with eigenvalues

, the transition to a ﬁnal state |f canhappenonlyifitisalsoan

eigenstate of J

and J

with the same eigenvalues :

f,j

|i, j

 = δ



h (1.121)