Basdevant J.-L., Rich J., Spiro M. Fundamentals in Nuclear Physics: From Nuclear Structure to Cosmology

Подождите немного. Документ загружается.

6.3 Fission mechanism, ﬁssion barrier 293

−1

−2

−4

photo−fission

236

−3

cross−section (barns)

E (MeV)

2010

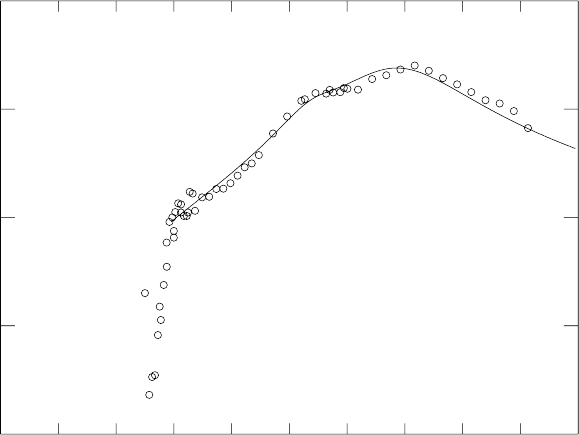
Fig. 6.5. Cross-section for γ

236

U → ﬁssion [30].

236

U to make the probability for ﬁssion reasonably large. This energy is

expected to be somewhat less than the height of the barrier E

∆E

∼ E

− 1MeV . (6.13)

This is because it is not necessary to add enough energy to erase the barrier

but only enough to make the tunneling rapid.

Table6.1liststhevaluesof∆E

for selected nuclei in the region 230 <

A<240. They are all of the order ∆E

∼ 6MeV.

A second way to induce ﬁssion of a nucleus (A, Z) is through neutron

absorption by the nucleus (A − 1,Z):

A−1

→

∗

→ ﬁssion . (6.14)

The eﬀective threshold for neutron-induced ﬁssion, i.e. the minimum neu-

tron kinetic energy necessary to give a large probability for inducing ﬁssion,

(A − 1) = ∆E

(A) − S

(A) , (6.15)

where S

is the neutron-separation energy of the nucleus A, i.e. the energy

necessary to remove a neutron. The reasoning behind this formula is illus-

trated in Fig. 6.6 which shows the levels of the systems A = 236 and A = 239

involved in the ﬁssion of

236

Uand

239

U. The ground states of these two nu-

clei can be transformed to a ﬁssionable state by adding an energy (by photon

294 6. Fission

Table 6.1. Fission threshold energy ∆E

and neutron separation energy S

for

selected nuclei (A, Z). ∆E

gives the eﬀective threshold for photo ﬁssion. The

eﬀective threshold for neutron-induced ﬁssion of the nucleus (A −1) is T

= ∆E

−

. For the three odd-(A − 1) nuclei, T

< 0 so ﬁssion can be induced by thermal

neutrons.

Fissioning ∆E

(threshold) neutron

nucleus (MeV) (MeV) (MeV) target

(A, Z)(A, Z) (A,Z) (A − 1,Z)(A − 1,Z)

234

U5.46.9

233

236

U5.76.3

235

240

Pu 5.5 7.3

239

233

Th 6.4 5.1 1.3

232

235

U 5.8 5.3 0.5

234

239

U 6.0 4.8 1.2

238

235

U+n

236

5.7MeV

fission

239

238

U+n

6.0MeV

4.8MeV

6.3MeV

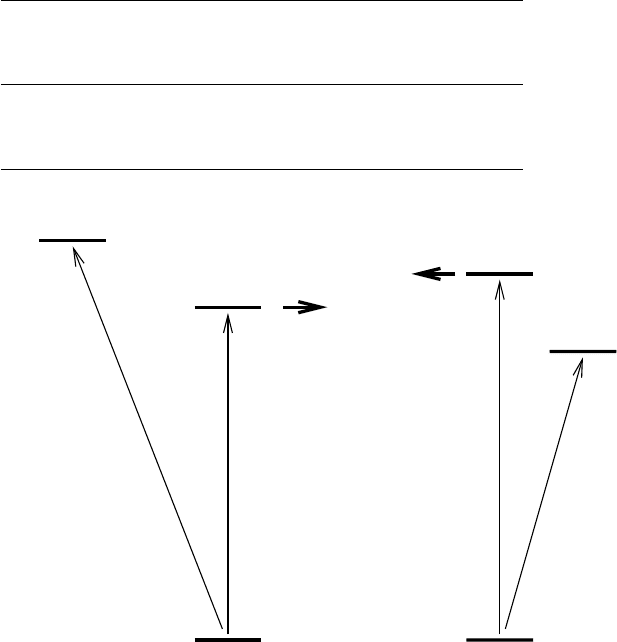
Fig. 6.6. Levels of the systems A = 236 and A = 239 involved in the ﬁssion of

236

U and

239

U. The addition of a motionless (or thermal) neutron to

235

U can lead

to the ﬁssion of

236

U. On the other hand, ﬁssion of

239

U requires the addition of a

neutron of kinetic energy T

=6.0 − 4.8=1.2 MeV.

6.4 Fissile materials and fertile materials 295

absorption) ∆E

equal to 5.7MeV (

236

U) or 6.0MeV (

239

U). A neutron can

be removed from the ground states of these two nuclei by adding an energy

(by photon absorption) S

equal to 6.3MeV (

236

U) or 4.8MeV (

239

U). We

see that a

235

U nucleus with a free neutron is at a higher energy than the

lowest ﬁssionable state of

236

U. The addition of a motionless (or thermal)

neutron to

235

U can thus lead to the ﬁssion of

236

U. On the other hand, a

238

U nucleus with a free neutron is at a lower energy than the lowest ﬁs-

sionable state of

239

U, so the addition of a motionless (or thermal) neutron

238

U cannot lead to the ﬁssion of

239

U but only to the radiative capture

of the neutron. Fission of

239

U requires the addition of a neutron of kinetic

energy T

=6.0 − 4.8=1.2MeV.

The last column of Table 6.1 gives the values of the neutron-induced

ﬁssion threshold for selected nuclei. Odd-N target nuclei are ﬁssionable by

thermal neutrons (T

< 0), whereas even-N nuclei have a threshold for the

kinetic energies of incident neutrons. As illustrated in Fig. 6.6, this is because

the last neutron of an odd-N ﬁssioning nucleus is less bound then the last

neutronofaneven-N ﬁssioning nucleus, as reﬂected in the pairing term

[δ(A)=34A

−3/4

] in the Bethe–Weizs¨acker semi-empirical mass formula.

Figure 6.7 shows the neutron-induced ﬁssion cross-sections for

235

Uand

238

U. The cross-section for

238

U exhibits the expected eﬀective threshold at

E ∼ 1.2 MeV. The threshold-less cross-section on

235

U exhibits the charac-

teristic 1/v behavior for exothermic reactions at low energy.

6.4 Fissile materials and fertile materials

The nuclei which are most easily used as fuel in ﬁssion reactors are the three

even-odd nuclei

233

235

Uand

239

Pu which ﬁssion rapidly by thermal neu-

tron capture.

Of the three ﬁssile nuclides, only

235

U exists in signiﬁcant quantities on

Earth, which explains its historical importance in the development of nu-

clear technology. Terrestrial uranium is (at present) a mixture of isotopes

containing 0.72%

235

U and 99.3%

238

On the other hand,

239

Pu and

233

Uhaveα-decay lifetimes too short to be

present in terrestrial ores. They are produced artiﬁcially by neutron capture

starting from the fertile materials

238

Uand

232

Th:

238

U →

239

U γ (6.16)

239

U →

239

Np e

−

1/2

=23.45 m

239

Np →

239

Pu e

−

1/2

=2.3565 day

and

232

Th →

233

Th γ (6.17)

296 6. Fission

46 8

1010101010

E(eV)

fission

cross−sect

on (

arns)

−4

−2

−4

−2

(n, γ)/100

(n, γ)

235

238

−2

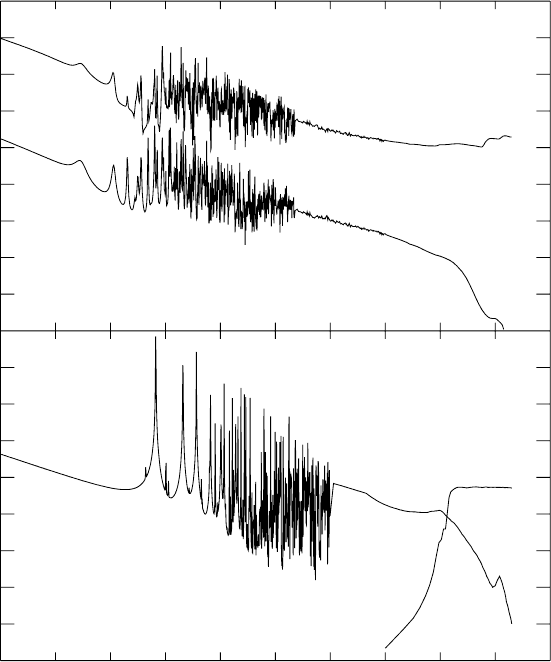
Fig. 6.7. Neutron-induced ﬁssion and radiative-capture cross-sections for

235

U and

238

U as a function of the incident neutron energy. The ﬁssion cross-section on

238

has an eﬀective threshold of ∼ 1.2 MeV while the cross-section on

235

U is propor-

tional, at low energy, to the inverse neutron velocity, as expected for exothermic

reactions. Both ﬁssion and absorption cross-sections have resonances in the range

1eV <E<10 keV.

6.5 Chain reactions 297

233

Th →

233

Pa e

−

1/2

=22.3m

233

Pa →

233

−

1/2

=26.967 day

In particular, a reactor which burns

239

Pu and which contains

238

Urods,

can produce more Plutonium than it actually consumes owing to the chain

(6.16). This is the principle of fast breeder reactors.

6.5 Chain reactions

The induced ﬁssion of

235

U → A+B+νn , (6.18)

creates on average

ν ∼ 2.5 neutrons. These secondary neutrons can induce

the ﬁssion of other

235

U nuclei. When they are emitted in a ﬁssion reaction,

the neutrons have a large kinetic energy, 2 MeV on the average. They can

be brought back to thermal energies by exchanging energy with nuclei in the

medium via elastic scatters.

Since

ν>1, a multiplicative eﬀect can occur. The number of neutrons

will be multiplied from one generation to the next and the reaction rate

increases accordingly. This is called a chain reaction. In order to evaluate

the possibility for a chain reaction to occur, we must know the number k of

ﬁssion neutrons which will eﬀectively induce another ﬁssion. The number k

is less than

ν because a certain fraction of the neutrons will be absorbed by

non-ﬁssion reactions or diﬀuse out of the region containing the

235

If k>1, the chain reaction occurs. This case is called the supercritical

regime. If k<1, the reaction does not develop, i.e. the sub-critical regime.

The limit k = 1 is called the critical regime.

The only inherent neutron-loss mechanism is radiative capture on the

nucleus constituting the fuel

U → γ

A+1

U σ ≡ σ

(n,γ)

. (6.19)

If this is the only loss mechanism, then the number of neutrons that induce

ﬁssion will be



= ν

ﬁs

+ σ

(n,γ)

. (6.20)

Table6.2givesthevaluesof



for pure

235

238

U, and

239

Pu under

conditions where the neutrons are “fast” (E

∼ 2 MeV) and thermalized

∼ 0.025 eV). For fast neutrons, absorption on

235

Uand

239

Pu is unim-

portant but for

238

U the large absorption cross-section reduces the number

of available neutrons from

ν =2.88 to ν



=0.52, i.e. sub-critical. For thermal

neutrons, absorption reduces the number of available neutrons by ∼ 25% for

235

Uand

239

Pu while, as already noted, there are no ﬁssions of

238

298 6. Fission

Table 6.2. Comparison of selected conﬁgurations for nuclear reactors with the last

column giving the number k of ﬁssion-produced neutrons available to induce further

ﬁssions. It is necessary to have k ≥ 1 for a chain reaction to occur. The neutron en-

ergy E

∼ 2 MeV corresponds to “fast” neutron reactors while E

∼ 0.025 eV corre-

sponds to “thermal” neutron reactors. The fuels shown are pure isotopes of uranium

and plutonium as well as the natural terrestrial mixture of uranium (0.7%

235

U) and

a commonly used enriched mixture (2.5%

235

U). σ

ﬁs

and σ

(n,γ)

are the cross-sections

(in barns) for neutron induced ﬁssion and radiative neutron capture (appropriately

weighted for the isotopic mixtures).

ν is the mean number of neutrons produced per

ﬁssion and



is the mean number after correction for radiative capture on the fuel

mixture. Finally, for thermal neutrons we show, in the ﬁnal column, the number

of neutrons k after multiplying by δ (Table 6.3) to account for neutron losses from

radiative capture on the thermalizing medium (moderator). The three thermalizers

are normal water, heavy water, and carbon.

fuel σ

ﬁs

(n,γ)

ν ν



∼ 2 MeV

235

U 1.27 0.10 2.46 2.28 = ν



238

U 0.52 2.36 2.88 0.52 = ν



239

Pu 2 0.10 2.88 2.74 = ν



∼ 0.025 eV

233

U 524 69 2.51 2.29 1.72 (

2.2 (

2.0 (C)

235

U 582 108 2.47 2.08 1.56 (

2.0 (

1.8 (C)

238

U 02.7000

239

Pu 750 300 2.91 2.08 1.56 (

2.0 (

1.8 (C)

0.7%

235

U 4.07 3.5 2.47 1.33 0.99 (

1.3 (

1.16 (C)

2.5%

235

U 14.5 5.4 2.47 1.8 1.37 (

1.8 (

1.6 (C)

6.6 Moderators, neutron thermalization 299

Reactors using uranium as fuel generally have mixtures of the two iso-

topes

238

Uand

235

U. It is therefore necessary to take into account ﬁssion and

absorption by both isotopes. For mixtures not to far from the natural terres-

trial mixture, f

235

=0.007, fast neutron ﬁssion and absorption is dominated

by the primary isotope

238

U. On the other hand, for thermal neutrons ﬁssion

is due entirely to

235

U while absorption is due to both

235

Uand

238

Usofor

thermal neutrons



= ν

235

ﬁs,235

235

(σ

ﬁs,235

+ σ

(n,γ),235

)+(1− f

235

)σ

(n,γ),238

. (6.21)

As shown in Table 6.2, the natural mixture gives a number of available

neutrons



=1.33 while increasing f

235

to 0.025 increases the number to



=1.8.

At this point, the values of



in Table 6.2 tell us that fast neutron reactors

can work with

239

Pu or, with somewhat less eﬃciency, with pure

235

U. For

reactors using thermal neutrons, the values of



indicate that a variety of

fuels can yield chain reactions. However, before concluding, we must calculate

the number of neutrons lost in the thermalization process. This is done in

the next section.

6.6 Moderators, neutron thermalization

The cooling of ﬁssion neutrons is achieved through elastic collisions with

nuclei of mass ∼ Am

in a moderating medium, as represented in Fig. 6.8.

In such a collision, the ratio of ﬁnal to initial neutron energies as a function

of center-of-mass scattering angle θ is



/E =(A

+2A cos θ +1)/(A +1)

. (6.22)

Assuming isotropic scattering in the center-of-mass, a good approximation

for neutron energies less than ∼ 1 MeV, one has on the average :

E



/E =(A

+1)/(A +1)

. (6.23)

The energy exchange is most eﬃcient for

H(A = 1) where half the energy is

lost in a collision, and becomes very ineﬃcient for A  1. We will see shortly

that a number that is more useful than the mean of E



/E isthemeanofits

logarithm:

log(E/E



) = −



−1

log[E



/E]d cos θ

=1−

(A − 1)

log

(A +1)

A − 1

. (6.24)

(For A = 1 this expression reduces to log(E/E



) =1.)

300 6. Fission

ast

c scatters

Fig. 6.8. A series of neutron–nucleus elastic scatters leading to the thermalization

of the neutron.

Consider a series of collisions as represented in Fig. (6.8). The center-of-

mass scattering angles are θ

,θ

, ···θ

.Aftern collisions, the mean neutron

energy E

is given by



i=1

i−1

⇒ log E



i=1

log(E

i−1

) , (6.25)

and, in a series of random collisions, there will be after n collisions :

log(E

) = nlog(E



/E) . (6.26)

The average number of collisions N

col

which are necessary in order to

reduce the energy of ﬁssion neutrons from E

ﬁs

∼ 2 MeV to the thermal

energy E

∼ 0.025 eV, is given by :

col

log (E

ﬁs

)

log(E/E



)

, (6.27)

with the denominator as a function of A given by (6.24) For the three mod-

erators

H (light water

O) A = 1,

H (heavy water

O) A = 2, and

C (graphite or CO

) A = 12, the values of N

col

, are given in Table. 6.3.

As expected, hydrogen is the most eﬃcient thermalizer, requiring only ∼ 18

collisions, while carbon requires 115.

Neutrons may be lost during the thermalization process by radiative cap-

ture on the thermalizing nuclei. Per collision, the probability is

p =

(n,γ)

+ σ

(n,γ)

, (6.28)

where σ

(n,γ)

and σ

are the cross-sections for radiative capture and elastic

scattering. The value of p is given for the three moderators in Table 6.3.

The probability that the neutron not be absorbed during the thermaliza-

tion process,

δ =(1− p)

col

, (6.29)

6.7 Neutron transport in matter 301

Table 6.3. Comparison of the three most commonly used neutron moderators in

nuclear reactors, water, heavy water and graphite. The cross-sections per molecule

for elastic scattering and radiative absorption are σ

and σ

(n,γ)

. The probability p

for absorption per collision is given by the ratio of the elastic cross-section and the

total cross-section. The number of elastic collisions N

col

necessary to thermalize a

neutron with E

∼ 2 MeV is given by (6.27). The last column gives the probability

of neutron survival during thermalization.

(n,γ)

p = σ

(n,γ)

/σ

tot

col

δ =(1− p)

col

O 44.8 0.664 1.5 × 10

−2

18 0.76

O 10.4 10

−3

9.6 × 10

−5

25 0.998

C4.74.5×10

−3

9.6 × 10

−4

115 0.895

is given in the last column to Table 6.3.

For nuclear reactors using thermal neutrons, the ﬁnal number of available

neutrons for ﬁssion is found by multiplying



in Table 6.2 by δ from Table

6.3togetk as the last column in Table 6.2.

From the last column of Table 6.2, we see that there are three main types

of theoretically feasible reactors:

• Natural uranium reactors using heavy water or carbon as moderators.

• Enriched uranium reactors. A 2.5% enrichment in

235

U allows the use of

light water as the moderator.

• Fast neutron reactors work without moderators. The most eﬃcient fuel is

239

Pu with k =2.74. The neutron ﬂux is suﬃciently high that one often

adds a mixture of uranium (generally depleted in

235

U after previous use

as nuclear fuel) that results in a production of

239

Pu through neutron

capture on

238

U (6.16). Such breeder reactors can actually produce more

fuel (

239

Pu) than they consume. Breeder reactors are more complicated

than those using thermal neutrons because, in order to avoid thermalizing

the neutrons, a liquid containing only heavy nuclei (usually sodium) must

be used to evacuate heat from the reactor core.

6.7 Neutron transport in matter

In the previous two sections, we evaluated the possibility for creating nuclear

chain reactions by considering the number of neutrons produced in a ﬁssion

event, and the number of neutrons lost through radiative capture on fuel and

moderating nuclei. Here we will consider additional losses due to neutrons

escaping outside the sides of the reactor. Roughly speaking the fuel must have

302 6. Fission

a size at least as large as the neutron mean-free path so that the neutrons

have a reasonable probability of creating further ﬁssions before escaping.

To go beyond this rough estimate requires a very detailed and complicated

analysis. More generally, the construction and the operating of a nuclear

reactor require the mastery of the distribution of neutrons both in energy

and in space. This is called neutron transport in the reactor. It is a very

involved problem which necessitates the elaboration of complex computer

codes. Several processes occur in the history of an individual neutron; its

formation in a ﬁssion, its elastic collisions with the various nuclei which are

present inside the medium, in particular its slowing down by the nuclei of

the moderator, its radiative capture, and ﬁnally the new ﬁssion that it can

induce. Besides that, in a ﬁnite medium, one must also consider the number

of neutrons that will be lost because they diﬀuse out of the region containing

the fuel. This constraint corresponds to the concept of a “critical mass” of

fuel, below which geometric losses necessarily lead to a sub-critical situation.

A glance at Fig. 6.9, which shows an actual fuel element (which is itself

plunged into the water-moderator) illustrates why the neutron transport is

a complicated problem, although all basic ingredients, i.e. the elementary

cross-sections and the geometrical architecture of all materials are known.

A detailed study of neutron transport is far beyond the scope of this

text. It is both fundamental in nuclear technologies and very complicated

to solve. The transport equation is an integro-diﬀerential equation whose

numerical treatment is in itself an artistry which has been steadily developed

for decades in all nuclear research centers. Its complexity comes in part from

the fact that it treats the behavior of neutrons both as a function of energy

(they can lose energy in collisions) and in space (they scatter). All R&D

organizations involved in this problem possess their own “secrets” to address

it. Calculations of neutron transport use the Boltzmann equation formalism.

In Appendix D we give some indications about how this equation appears in

the speciﬁc case of neutron transport.

Here, we will consider the problem in a very simple approximation, in

order to exemplify why and how the concept of a “critical mass” emerges.

The problem is quite simpler if we make the, not totally absurd, assumptions

that the neutrons all have the same time-independent energy, and that the

medium is homogeneous, though ﬁnite in extent.

6.7.1 The transport equation in a simple uniform spherically

symmetric medium

We treat a simple system consisting a pure

239

Pu fuel with no moderator.

The lack of light nuclei in the medium allows us to make the approximation

that neutrons do not loose energy in elastic collisions, which simpliﬁes things

considerably.