Barnes D.J., Chu D. Introduction to Modeling for Biosciences

Подождите немного. Документ загружается.

7.4 Practical Implementation Considerations 293

1. Initialization:

• Set the simulation time to zero, and initialize the random number generator.

• Set up data for the reactions to be modeled: reaction constants and numbers of

each type of molecular species.

• Build a dependency graph of reactions.

• Calculate the propensity value a

for each reaction and the cumulative propen-

sity a

• Calculate the minimum propensity value a

min

• Assign each reaction to group n such that a

min

n−1

<=a

min

2. Iteration:

• Generate uniform random numbers, r

, r

, from the unit range.

• Set the time increment, τ =(1/a

) log

(1/r

• Use r

to select a group.

• Repeatedly generate random numbers r

and r

until a reaction, μ, is selected

from the group.

• Adjust the reactant and product levels according to reaction μ.

• Output the time and molecular levels, if required.

• Generate new a

values for reactions affected by the last reaction, adjusting

group membership accordingly.

Fig. 7.9 Outline of the SSA-CR method

of the group’s reactions have revised propensities. We will consider this step further

in Sect. 7.4 because its efﬁcient implementation is important to the scalability of the

algorithm.

If it is possible to determine accurately a

max

at the start of the model then mov-

ing groups does not present a problem because all possible groups will have been

provided for in the propensity tree. However, if a

max

could not be determined in

advance, and the number of groups expands into the range of the next power of two,

then the propensity tree will require rebuilding with an additional level in the mid-

dle of simulating the reactions. This is not disastrous, but the possibility needs to be

taken account of in the implementation and will have a small effect on the runtime,

as it is a relatively expensive operation.

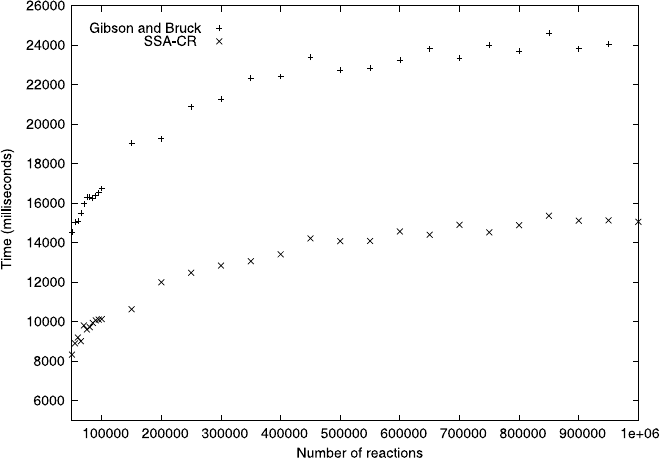
Figure 7.10 displays a comparison between the runtime performances of imple-

mentations of the Gibson-Bruck and SSA-CR methods. As can be observed, the

averaged runtime for the SSA-CR implementation rises less steeply than for the

Gibson-Bruck algorithm as the number of reactions increases. However, it is still

some way off being the O(1) we were looking for and we will discuss some of the

reasons for this in Sect. 7.4.

7.4 Practical Implementation Considerations

One of the reasons we have considered a number of different approaches to the

implementation of stochastic simulations is that, aside from the accuracy of the

294 7 Simulating Biochemical Systems

Fig. 7.10 Mean run times in milliseconds for 1,000,000 iteration steps for our implementations of

the Gibson-Bruck and SSA-CR algorithms, with random reaction sets

modeling, our primary concern is likely to be having a fast runtime for our models.

We have discussed the theoretical runtime scaling complexity of the different meth-

ods but, in practice, we may ﬁnd that our programs are unable to match up with

these. Why is this? The two principle reasons are: the way we have implemented

the algorithms and the environment in which we run the programs. In this section

we will look at the effect of both of these issues.

7.4.1 Data Structures—The Dependency Tree

In Sect. 7.2 we illustrated that Gibson and Bruck were able to signiﬁcantly reduce

the time complexity of Gillespie’s method, in part through the use of additional data

structures for storing reaction dependencies and putative reaction times. Appropriate

data structure selection is crucial to runtime performance, as we can easily illustrate

with the building of the reaction dependency graph.

In all these algorithms, there are clearly two distinct phases of the modeling

process: setup of the reaction structures prior to simulation, and the simulation itself.

In analyzing complexity, we have tended to completely ignore the setup element

because it occurs just once, whereas the simulation involves repeating a series of

steps an enormous number of times—suggesting that the simulation time will tend

to dominate the setup time. However, consider the approach we used in building

7.4 Practical Implementation Considerations 295

the dependency tree in Code 7.5 and note that its complexity is O(M

) because

each reaction is checked against every other for its effect. When dealing with large

numbers of reactions, this version would add signiﬁcantly to the overall runtime—

for practical purposes it does not scale. How can we improve on it? The key is

to recognize that dependency arises via the molecular species, and that both the

number of molecules affected by a single reaction, and the number of molecules

a reaction depends on will often remain fairly constant with increasing numbers

of reactions. So Code 7.9 offers a much more efﬁcient approach to building the

dependency graph. For each reaction, we record which molecules it depends on in

a temporary molecule-dependency list, and then use that intermediate data structure

to determine which reactions are affected by each other. It is worth noting that we

end up with exactly the same data structure for the dependency graph as in the

original version, but the complexity of the building process is more like O(M) rather

than O(M

7.4.2 Programming Techniques—Tree Updating

We can further illustrate the impact of our implementation choices on runtime with a

look at the way in which the propensity tree of the SSA-CR method is updated. The

tree holds the group propensity values in its leaves and the cumulative propensity

value, a

, in its root. Each time a reaction’s propensity is affected by the occurrence

of another reaction, its group’s propensity must be adjusted. In Sect. 7.3.2 we noted

that it is best to defer updating the propensity tree until all the group changes are

known at the end of a single step, rather than updating it each time a reaction’s

propensity is adjusted. That way we can avoid multiple updates to the tree for the

same group. We suggested storing the changed groups’ identities in a set to avoid

updating the tree multiple times for the same group. The idea is that, once all the

individual reaction changes have been implemented within the groups, each leaf

value for the changed groups is updated and trickled up to the root. However, the

process of updating the tree deserves further consideration because it still potentially

involves some duplication of effort. Consider the case where two groups’ leaves

have the same parent node in the tree and both group’s propensities have changed

following a reaction. If the leaf-to-root update is made separately for each leaf,

then most of the work of the ﬁrst update will be overwritten by the second. The

update process can be streamlined a little, therefore, by actually storing the set of

parent nodes of the group leaves that have been adjusted and recalculating the parent

values as the sum of their two child values, regardless of whether one or both child

values has been adjusted. However, we can take this even further by recognizing

that updating from two leaves with different parent nodes but a common grandparent

node will also involve duplication of update from the grandparent node upwards, and

the argument can be continued for different ancestry levels within the tree. What we

have actually done in our implementation, therefore, is to trickle each update only to

the next level above in the tree, and then repeated this process for each level, until all

the changes eventually accumulate in the root. Each changed node is only updated

once with this approach.

296 7 Simulating Biochemical Systems

/**

* Build the dependency graph for the reactions.

private void buildDependencyGraph()

{

// Map of molecules to the list of reactions depending on them.

Map<Molecule, List<Reaction>> moleculeDependencyList =

new HashMap<Molecule, List<Reaction>>(molecules.size());

// Build a map of which reactions depend on which molecules.

for(Reaction target : reactions) {

Set<Molecule> dependsOn = target.getDependsOn();

for(Molecule m : dependsOn) {

List<Reaction> dependency =

moleculeDependencyList.get(m);

if(dependency == null) {

dependency = new ArrayList<Reaction>();

moleculeDependencyList.put(m, dependency);

}

dependency.add(target);

}

// For each reaction, identify which molecules it affects

// and which reactions depend on those molecules.

for(Reaction source : reactions) {

// Create the set for affected reactions.

Set<Reaction> affectedReactions = new HashSet<Reaction>();

// Add the self dependency.

affectedReactions.add(source);

// Identify the reactions affected.

Set<Molecule> affects = source.getAffects();

for(Molecule m : affects) {

List<Reaction> dependency =

moleculeDependencyList.get(m);

if(dependency != null) {

affectedReactions.addAll(dependency);

}

dependencyGraph.put(source, affectedReactions);

}

Code 7.9 Improved building of a reaction dependency graph (see Code 7.5 for comparison)

7.4.3 Runtime Environment

Aside from implementational effects on overall runtime, there will be potentially

signiﬁcant effects from the hardware on which a program is run, the operating sys-

tem environment and the programming language. An obvious factor is the amount

of memory available to the program, and the way it is managed by the runtime en-

vironment and operating system. When discussing the comparison in Fig. 7.10,we

7.5 The Tau-Leap Method 297

noted that our implementation of SSA-CR did not appear to be giving the O(1)

behavior for increasing numbers of reactions we had anticipated. One of the po-

tential reasons for this is the effect of memory management within a Java runtime

environment. The garbage collector, responsible for recycling out-of-date objects,

is an ever-present element in Java programs. Depending on how the Java runtime

is conﬁgured, this can result in either periodic pausing of the model for garbage

collection, or a continual underlying overhead in the runtime. While this might be

seen as a disadvantage of Java, the corresponding advantage of memory security

is hard to dismiss. Furthermore, just because memory management is not always

automatically managed in other languages does not mean that the implementor is

thereby freed from having to worry about it. The need to manage memory carefully

will always be an issue with large simulations and is left entirely in the hands of the

programmer in many programming languages. Pitfalls for the unwary are legion!

In addition, memory and processor contention from other processes running on

the same machine may be hard to avoid without exclusive access to the available

resources, and will apply regardless of the programming language used.

7.5 The Tau-Leap Method

Aside from the work of Gibson and Bruck and Slepoy et al., there have been a num-

ber of variations of the SSA proposed for the purpose of improving performance.

The tau-leap method [22] is one of these. At its heart is the recognition that one of

the fundamental costs of the SSA is that the exact effect of every single reaction

taking place is explicitly modeled. With the tau-leap approach, a time frame, τ ,is

chosen and the multiple reactions that occur within it are all acted on together. This

approach necessarily represents an approximation in comparison to the exact SSA,

and the balance between simulation accuracy and speed up lies in the appropriate

selection of the leap distance.

The number of times that a given reaction with propensity a

will take place

within the τ period is calculated from a Poisson random distribution with mean

λ = a

τ . There is clearly a gotcha in this method in that there is potential for the

number of molecules in a species to become negative if τ is set too high; on the

other hand, setting it too low reduces the potential efﬁciency gains. The right value

is likely to vary with the dynamic state of the system.

While we do not discuss this method in any further detail, it is worth being aware

of it because it is often offered in modeling toolkits, such as Dizzy (which we look at

in Sect. 7.6), and it can offer a signiﬁcant reduction in execution time if appropriate

for the model.

7.6 Dizzy

So far in this chapter, we have introduced a succession of approaches to modeling

reactions stochastically. We have illustrated how they might be implemented in the

298 7 Simulating Biochemical Systems

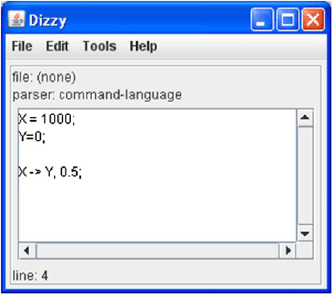
Fig. 7.11 The Dizzy editor

window with CMDL

commands for an

isomerization reaction

form of Java class deﬁnitions in order to provide insights into some of the practi-

calities of using the different algorithms. Although these sample programs could be

used to model reaction sets in the way we have illustrated, we have not sought to

provide a full programming environment to the reader, primarily because a number

of modeling environments already exist. One of these is Dizzy [32, 33].

Dizzy provides implementations of the Gillespie and Gibson-Bruck algorithms

as well as the tau-leap approximation (Sect. 7.5), for instance. It has a GUI that

incorporates features for displaying results, but its code can also be accessed in the

form of libraries via an application programmer interface (API) for incorporation

into other programs. Dizzy is freely distributed under the terms of the GNU Lesser

General Public License (LGPL) [15]. In this section, we will brieﬂy introduce the

features of Dizzy.

When Dizzy is started it brings up an editor window. A model can be created

directly within this window, or prepared externally in a text ﬁle and loaded via the

File menu option. The preferred sufﬁx for such ﬁles is .cmdl to match Chemical

Model Deﬁnition Language (CMDL), the language used to deﬁne the reaction sets.

Figure 7.11 illustrates the editor window with the following CMDL commands for

the isomerization reaction of (7.5):

// Reaction parameters

re1, X = 1000;

re2, Y = 0;

re3, X -> Y, 0.5;

Each command is terminated by a semicolon. Symbols for the molecular species

are deﬁned in assignment statements containing the initial species size (re1 and

re2). The reaction deﬁnition includes the value of the reaction constant parameter,

separated by a comma from the reactants and products (re3).

7.6 Dizzy 299

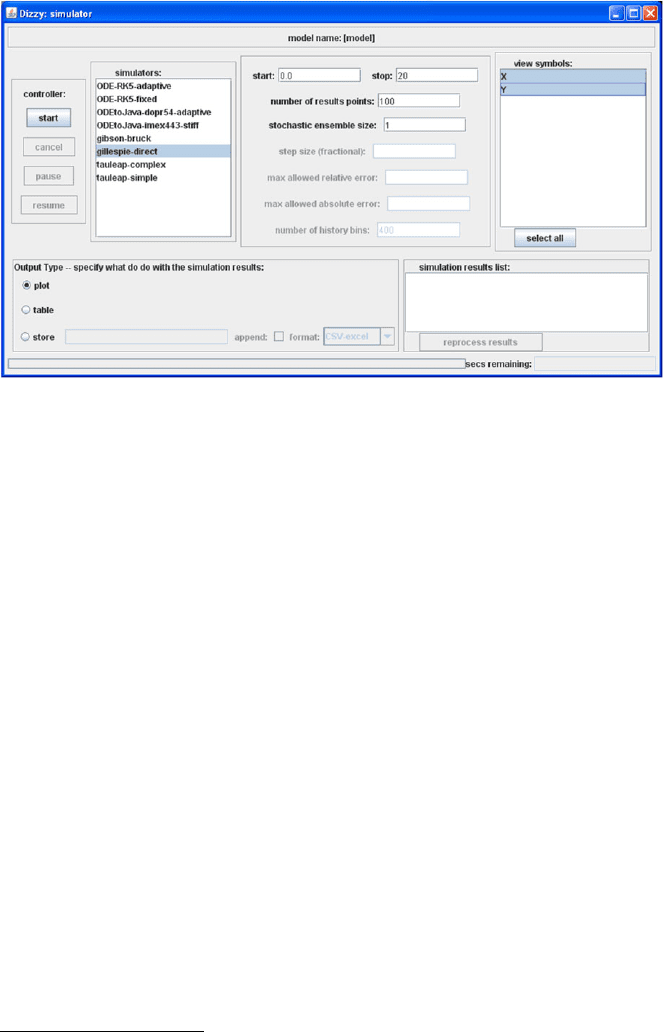
Fig. 7.12 The Dizzy simulator controller dialog window

Once a model has been deﬁned completely it can be run by selecting the Tools

→ Simulate menu item.

Figure 7.12 shows the simulator controller dialog window

where the simulator type (Gillespie, Gibson-Bruck, etc.) is selected, along with the

species to be monitored in the output, and the stop time. We have selected a stop

time of 20 and to view the population numbers of both species against time in the

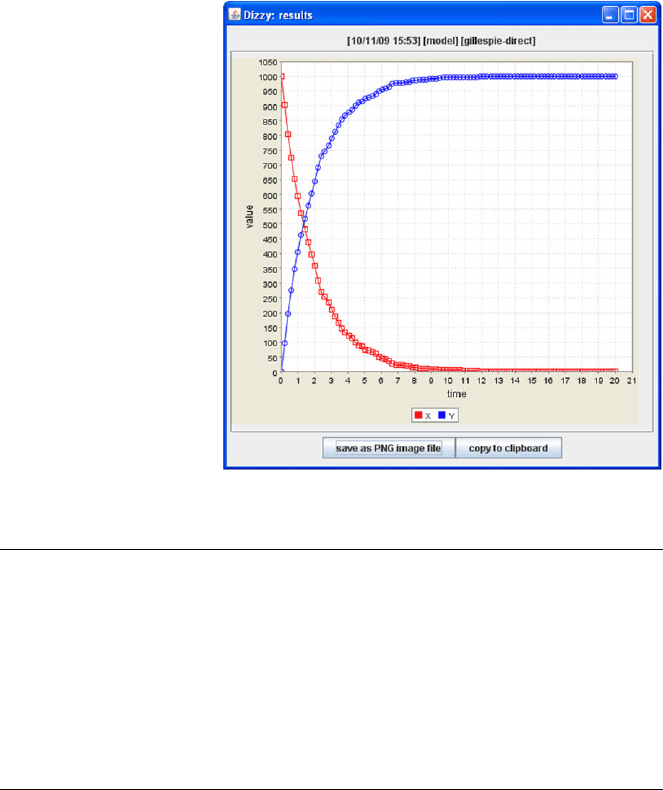
output. At the end of the run, a visualization of the output is displayed (Fig. 7.13).

Deﬁning species’ names and initial population levels is a particular example of

the ability to associate names with values and expressions. Code 7.10 is a CMDL

version of the reactions shown in (7.6) which illustrates this.

In the ab reaction, species B is preﬁxed with a dollar symbol to show that it is

a boundary species. Notice that we have used comments to make the model more

readable, and named the reaction constants. The deﬁnition of the constant ad_prob

involves an expression based on the value of ab_prob. Expressions written like

this are always evaluated immediately but there is also a syntax to delay evalua-

tion until runtime. This is particularly useful for reaction probabilities that are not

constant but either time-dependent or species-dependent. An expression written be-

tween square brackets is a deferred evaluation expression. Each time the reaction

probability is required the expression will be re-evaluated. In the following exam-

ple, the reaction ab uses a constant probability value while the reaction ac uses the

special symbol time to indicate that its probability is time dependent. Note, too,

If the model has been deﬁned directly in the editor window rather than loaded from ﬁle, it may be

necessary to specify a parser; select command-language.

300 7 Simulating Biochemical Systems

Fig. 7.13 Display of results

within Dizzy

// The species and initial population levels.

A = 1000; B = 1000; C = 1000; D = 1000; E = 1000;

// Reaction parameters.

ab_prob = 0.12;

ad_prob = 2 * ab_prob / 3;

ce_prob = 0.5;

// Reactions.

ab, A + $B -> C, ab_prob;

ad, A + D -> E, ad_prob;

ce, C + E -> A + A + D, ce_prob;

Code 7.10 CMDL implementation of (7.6)

that the population size of species A has to be explicitly included in the expression,

while it is implicit in ab.

// The species and initial population levels.

A = 100.0; B = 0.0; C = 0.0;

// Reaction ac is time-dependent.

ab, A -> B, 0.1;

ac, A -> C, [0.1 * A * time];

7.7 Delayed Stochastic Models 301

7.7 Delayed Stochastic Models

A characteristic of all of the modeling algorithms we have looked at so far is that

reactions are assumed to take place instantaneously: reactants are consumed and

products produced with no passage of time and no intervening reactions taking

place. While this assumption may work satisfactorily for many of the situations

we wish to model, there are also many scenarios where taking account of reaction

duration may have a signiﬁcant effect on the overall outcome. It is for this reason

that some effort has gone into the idea of introducing delay formulations into the

speciﬁcations of reaction systems.

A speciﬁc use for delays can be found in the technique of collapsing chains of

similar reactions, such as the following, taken from Gibson and Bruck [19]:

A +B →S

→S

...

n−1

→S

→C +D

Where the intermediate products, S

...S

, play no independent role in other reac-

tions, there are clearly advantages to not having to represent the intermediate reac-

tions separately. The number of intermediate reactions may be very large and this

will have a negative impact on the runtime of the model. Instead, we can conceptu-

ally represent the chain above in the following way:

A +B →P

int

→C +D

in which a single module of an artiﬁcial intermediate product, P

int

, is produced.

int

is then converted, after a calculated delay, into the ﬁnal products of the chain.

The length of the delay and its determination depend, of course, on the character-

istics of the chain being collapsed. In Gibson and Bruck’s example of a chain of n

identical ﬁrst-order intermediate reactions the delay is based on a probability drawn

from a gamma distribution. However, where there is implementational support for

the principle of delays, they could be based on anything, including absolute time

intervals.

Delayed production of products can be introduced relatively easily into the Gille-

spie direct method [4, 37], as partially illustrated in Code 7.11. The idea is that a

queue of delayed products is maintained in addition to the reaction set. The queue is

ordered by the time at which the products should be added to the system. Before a

selected reaction is acted on at time τ, the head of the queue is checked for a pending

product. If the next pending product is due to be produced prior to time τ then the

product is produced and the pending reaction canceled. Cancellation is necessary

302 7 Simulating Biochemical Systems

public void run()

{

int step = 0;

ReactionSet system = new ReactionSet();

initModel(system);

// Obtain the initial cumulative propensity.

double aZero = system.calculateAZero();

time = 0;

// Stop when the simulation time has passed or

// no change possible.

while(time < stopTime &&

!(aZero == 0.0 && delayedProducts.size() == 0)) {

double deltaT = (1.0 / aZero *

Math.log(1.0 / Math.random()));

// See if a delayed product should be produced first.

PendingProduct p = delayedProducts.peek();

if(p != null && p.getProductionTime() <= time + deltaT) {

delayedProducts.remove();

p.produce();

time = p.getProductionTime();

}

else {

Reaction r =

system.findReaction(Math.random() * aZero);

time += deltaT;

r.react();

}

aZero = system.calculateAZero();

}

Code 7.11 Gillespie’s direct method with support for delayed reaction products (compare

Code 7.2)

because reaction propensity values are likely to change as a result of the product

being added to the system. In our implementation, the queue is populated through

a change to the behavior of the produce method (see Code 7.1) for delayed prod-

ucts. Delayed product objects calculate the time of their production, based on the

current simulation time, and place a PendingProduct object into the queue.

We have already identiﬁed that the Gillespie algorithms have the worst scaling

complexity of all of the algorithms we have considered in this chapter; the addition

of the queue adds further overheads to the basic iteration. Every delayed product

that is added to the queue will result in the work done to identify a future reaction

being wasted, for instance. It follows that, for large reaction systems, the unmodiﬁed

SSA is unlikely to be the most efﬁcient choice where large numbers of delays are

involved.

The inefﬁciency in adding delayed reactions to the Gillespie approach is due, in

part, to the iteration loop dealing with two distinct entities—reactions and products.