Barnes D.J., Chu D. Introduction to Modeling for Biosciences
Подождите немного. Документ загружается.

7.1 The Gillespie Algorithms 283
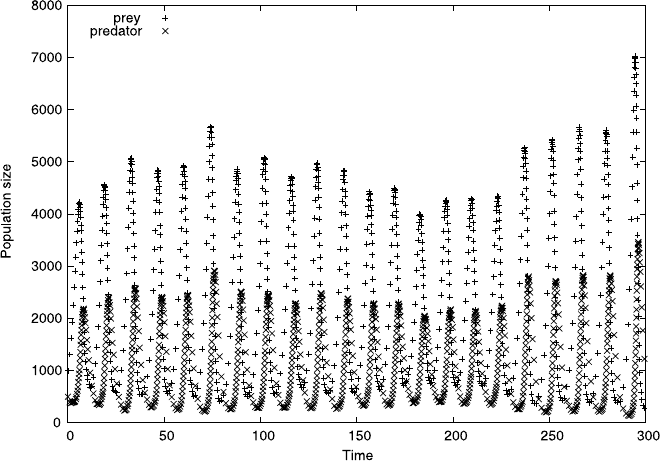
Fig. 7.6 Predator-prey population numbers from (7.9) with Y 1
0
= 1000, Y 2
0
= 500, c
1
= 0.5,
c
2
=0.0005, c
3
=0.5, c
4
=0.00025
and Z explicitly, or make a one-for-one replacement assumption, and (7.9)offersan
alternative formulation.
Y 1
c
1
→ 2Y 1 Prey reproduction
Y 1 +Y 2
c
2
→ Y 2 Prey death through predation
Y 2
c
3
→ Predator death
Y 1 +Y 2
c
4
→ Y 1 +2Y 2 Predator reproduction in the presence of prey
(7.9)
Figure 7.6 illustrates variations in population numbers of two species over a few
hundred iterations with a model based on (7.9). Notice how the peaks in predator
levels slightly trail those in prey levels and also that, from time to time, the levels of
both species come quite close to zero. Touching zero is perfectly possible within the
stochastic model; this would amount to a permanent population crash from which
the model cannot recover.
Having looked at Gillespie’s SSA approach, and a few small example models, we
will now look at some variations that seek to improve the scalability of the original
approach.
284 7 Simulating Biochemical Systems
1. Initialization:
• Set the simulation time to zero, and initialize the random number generator.
• Set up data for the reactions to be modeled: reaction constants and numbers of
each type of molecular species.
• Build a dependency graph of reaction products and reactants.
• Calculate the propensity value, a
i
, for each reaction.
• Calculate the next reaction time, τ
i
, for each reaction from an exponential
distribution with parameter a
i
. Store the τ
i
values in an indexed priority queue.
2. Iteration:
• Choose the reaction, μ, with smallest τ
i
.
• Set the current time to τ
μ
.
• Adjust the reactant and product levels according to reaction μ.
• Output the time and molecular levels, if required.
• Generate new a
i
and τ
i
values for reactions affected by the last reaction, and
update the indexed priority queue accordingly.
Fig. 7.7 Outline of the Gibson-Bruck next reaction method
7.2 The Gibson-Bruck Algorithm
Gibson and Bruck[19] developed a variation of Gillespie’s first reaction method
which they called the next reaction method. They sought to reduce the O(M) com-
plexity of the SSA by lowering the number of calculations on each iteration. In par-
ticular, they looked at the areas that produced the linear dependency on the number
of reactions, M:
• Recalculating the a
i
values.
• Recalculating the τ
i
values.
• Identifying the smallest τ
i
value.
It has already been noted in Sect. 7.1.1 that it is only necessary to recalculate the a
i
values of reactions whose reactant molecule levels were affected by the immediately
preceding reaction. As a result, the next reaction method is able to limit recalculation
of τ
i
values to only those reactions whose a
i
were changed. This optimization is
made possible by using absolute time for τ values rather than relative time.
Figure 7.7 shows an outline of how the next reaction method works. While very
similar in outline to the first reaction method, this more efficient version is often
overlooked in favor of the Gillespie methods. The reason for this appears to be
primarily because it requires additional data structures to support it; in particular, the
reactions’ dependency graph and the indexed priority queue of reaction times. There
is little rationale for avoiding Gibson-Bruck, if this is the reason, given the ready
availability of modern programming libraries of data structures. We will explore
these data structures in the following sections.

7.2 The Gibson-Bruck Algorithm 285
7.2.1 The Dependency Graph
The dependency graph has to be built just once, during the initialization stage. For
each reaction, it is necessary to identify which molecular species are affected by that
reaction. This is usually the set of all reactant and product molecules except (as in
the case of a catalytic reaction) where a reactant appears with equal multiplicity as a
product. In addition, we identify which species a reaction depends upon—typically
simply its reactants.
1
In Java, we can easily represent the dependency graph as a
map between a reaction and the set of reactions it affects:
Map<Reaction, Set<Reaction>> dependencyGraph
Code 7.5 shows the way in which a dependency graph can be built by iterating
over the full set of reactions and making the link between the molecular species
affected by each reaction and the reactions dependent on those species. We shall
come back to this task in Sect. 7.4 when we look further at wider efficiency consid-
erations.
7.2.2 The Indexed Priority Queue
The indexed priority queue can be represented as a binary tree data structure whose
nodes each consist of a reaction paired with its putative next reaction time. The tree
is ordered such that the time value of any node is always less than or equal to those
of both of its children. However, the children are not ordered. Such a data structure
is also called a heap. The advantage of maintaining this structure is that no search
is required to identify the next reaction—it is necessarily stored at the root of the
tree.
The tree can be implemented as an array with the property that a node stored at
index i has its parent node at index (i −1)/2 and child nodes at 2i +1 and 2i +2.
The length of the array is equal to the number of the reactions. Code 7.6 illustrates
the initial building of the tree during model setup. Note that the nodes are Reaction
objects, which we have modified from the version used with Gillespie to store their
putative next reaction time.
The ordering of the nodes in the tree will obviously change as reaction times
are updated. This is the most complex aspect of the next reaction method, yet it
is still straightforward to program. As long as the number of changes to the tree
is relatively modest compared with the number of reactions then this is one step
towards reducing the runtime speed complexity from O(M).
In addition to the tree that relates reactions to their time ordering, we need a data
structure to relate a reaction to its node in the tree. This is so that a node can be
1
We ignore here the indirect dependencies introduced through non-constant reaction probabilities
that are affected by non-reacting molecular species, although this is handled in the full version of
the code provided for this chapter.

286 7 Simulating Biochemical Systems
/**
* For each reaction, identify which molecular species it affects
* and which reactions depend upon those species.
*/
void buildDependencyGraph()
{
// Iterate over the list of reactions.
for(Reaction source : reactions) {
// Create a set for the reactions affected by
// the source reaction.
Set<Reaction> affectedReactions =
new HashSet<Reaction>();
// Get the species whose numbers are changed by
// this reaction.
Set<Molecule> affects = source.getAffects();
// Add the self edge.
affectedReactions.add(source);
// Identify all reactions affected.
for(Reaction target : reactions) {
Set<Molecule> dependsOn = target.getDependsOn();
for(Molecule m : dependsOn) {
if(affects.contains(m)) {
// target depends on one of
// the affected species.
affectedReactions.add(target);
}
}
}
// Store the set in the dependency graph.
dependencyGraph.put(source, affectedReactions);
}
}
Code 7.5 Building a reaction dependency graph (unoptimized)
updated with its new time when a reaction is affected by the occurrence of another.
In our case, we use a map relating a reaction to its integer index in timeOrdered-
Queue:
Map<Reaction, Integer> queueIndex;
Pseudo-code for updating the tree when a reaction’s next time is changed can be
seen in Code 7.7.
7.2.3 Updating the τ Values
What remains to be described is the way in which the τ
i
values of the affected
reactions are updated, as this is a key difference between the first reaction and next
reaction methods. Whereas the first reaction method requires new τ
i
values to be
generated afresh from an exponential distribution with the new a
i
values, the next

7.2 The Gibson-Bruck Algorithm 287
// The indexed priority queue.
private Reaction[] timeOrderedQueue;
...
/**
* Initialize the indexed priority queue.
*/
private void initQueue()
{
int numberOfReactions = reactions.size();
timeOrderedQueue = new Reaction[numberOfReactions];
for(int index = 0; index < numberOfReactions; index++) {
insertIntoQueue(index, reactions.get(index));
}
}
/**
* Insert reaction into the priority queue at the given index
* and bubble it upwards to its correct position.
*/
private void insertIntoQueue(int index, Reaction reaction)
{
timeOrderedQueue[index] = reaction;
// Make sure that the order is properly maintained.
int parentIndex = (index - 1) / 2;
Reaction parent = timeOrderedQueue[parentIndex];
// Bubble upwards, if necessary.
while(index > 0 &&
reaction.getNextTime() < parent.getNextTime()) {
swap(parentIndex, index, reaction);
index = parentIndex;
parentIndex = (index - 1) / 2;
parent = timeOrderedQueue[parentIndex];
}
}
Code 7.6 Building the initial state of the priority queue
reaction method only requires this for the reaction that has just taken place. For
all other affected reactions, their old τ values (τ
old
)areadjusted according to the
current time and the ratio between their old and new a
i
value in the way shown in
(7.10), where t is the (absolute) time of the most recent reaction.
2
τ
new
=t +(a
old
/a
new
)(τ
old
−t) (7.10)
The new τ values are then used to update the nodes in the priority queue, which will
be reordered as a consequence, leaving the next reaction at the root of the tree ready
for the following iteration.
2
Note that we ignore here the possibility that a
new
is zero, although this is handled in the full
version of the code provided for this chapter.
288 7 Simulating Biochemical Systems
updateTree(Node n)
{
Node parent = n.getParent();
if(n.getNextTime() < parent.getNextTime()) {
Swap n with its parent node;
// Continue upwards, recursively.
updateTree(n);
}
else {
Node child = child with smallest tau;
if(n.getNextTime() > child.getNextTime()) {
Swap n with child node;
// Continue downwards, recursively.
updateTree(n);
}
}
}
Code 7.7 Pseudo-code for recursively updating a node in the indexed priority queue
7.2.4 Analysis
There are several ways in which the next reaction method is faster for large numbers
of reactions than the first reaction method:
• Identification of the next reaction is immediate, given the indexed priority queue.
• Only one random number is generated per iteration—to calculate the new τ value
for the most recent reaction—rather than one per reaction
• Only the affected reactions must be considered for update at the end of the reac-
tion, and these are readily identified from the dependency graph.
The limiting factor for the complexity of the next reaction method is the dependen-
cies between the reactions. Where these are relatively few per reaction compared
with the overall number of reactions, M, then this method scales at the much slower
rate of O(log
2
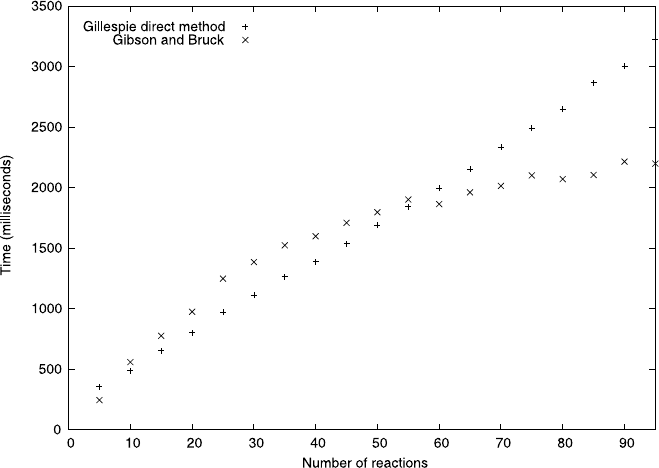
M) compared with O(M) for the first reaction method. Figure 7.8
provides illustrative timings from our implementations of both methods up to a few
hundred reactions. The difference is clear to see. Gibson and Bruck’s method is gen-
erally to be preferred over Gillespie’s, therefore, where the number of reactions is
large enough to be a consideration.
In their paper [19], Gibson and Bruck also discussed improvements to Gille-
spie’s direct method that improved its complexity to O(log
2
M). These involve the
use of a dependency graph, as in the next reaction method, and a binary tree to
store cumulative propensity values, which makes both the calculation of a
0
and
selection of the next reaction more efficient than in the original version. We will
look at the use of the binary tree in connection with another version of the SSA in
Sect. 7.3.
What we see in Gibson and Bruck’s approach is a reduction in runtime through
the use of more memory, in the form of the dependency tree and priority queue.
7.3 A Constant Time Method 289
Fig. 7.8 Mean runtime in milliseconds for 1,000,000 iteration steps for our unoptimized imple-
mentations of Gillespie’s direct method and the Gibson-Bruck algorithm, with random reaction
sets
While the data structures bring slightly increased implementational complex-
ity, they make practical both larger models and more runs of a model for in-
creased accuracy of results. This kind of tradeoff between speed and memory
is a recurring theme in algorithm design and implementation in computer sci-
ence.
7.3 A Constant Time Method
In 2008, Slepoy, Thompson and Plimpton [38] provided a further variation in the
implementation of the stochastic simulation algorithm. In ideal circumstances, their
algorithm scales as O(1)—in other words, independently of the number of reac-
tions. Where the number of reactions is very large, this has the potential to offer
significant speed advantages over both the Gillespie and Gibson-Bruck algorithms.
As one might expect, however, the speed improvements require a more complex
implementation.
Slepoy et al. noted that the SSA is a particular application from a general area
known as random variate generation (RVG) [13]. They took an existing RVG algo-
rithm and adapted it to apply to the SSA. Their approach is based on a technique
called composition and rejection, leading them to use the shorthand SSA-CR for it.
290 7 Simulating Biochemical Systems
The essence of the approach is to group together reactions with similar propensities
and select a group before selecting an individual reaction from within that group.
Each group has a lower-bound for the propensities of the reactions it contains. If
lwb(g) is the lower-bound propensity for group g, then a reaction with propensity
a
i
is placed in group g
n
, such that, lwb(g
n
)<= a
i
< lwb(g
n+1
). Successive pow-
ers of 2 times the minimum possible non-zero propensity value (a
min
) are used as
the boundary values for groups. The boundary values remain fixed for a particular
simulation run, but a reaction may move between groups as its propensity varies.
By grouping reactions in this way, much of the dependence of the algorithm on the
number of reactions, M, is removed, and hence a scaling independent of M becomes
possible. However, there are two assumptions required:
• The ratio of maximum to minimum probability for any two reactions must be
bounded.
• The average number of dependencies between reactions must remain fairly con-
stant and not grow in proportion to the total number of reactions.
Figure 7.9 shows an outline of the SSA-CR method.
7.3.1 Selection Procedure
The selection of the right group is based on the approach outlined in (7.2)forre-
action selection in Gillespie’s first reaction method. However, the implementation
illustrated in the findReaction method in Code 7.3 is a linear summation and
search, which is not particularly efficient—indeed, it is one of the elements that
contributes to the unoptimized first reaction method being O(M). An alternative,
which is applicable to both the first reaction method and the SSA-CR method, is to
store cumulative propensity values in a binary tree. In SSA-CR, the leaves corre-
spond to groups and store the sums of the reaction propensities within each group,
whereas in the first reaction method the leaves store the individual reaction propen-
sities. Each parent node stores the sum of the values in its two child nodes. As a
result, the root of the tree stores the sum of all group (and, therefore, all reaction)
propensities: a
0
. We can use the same style of tree implementation as that for the
indexed priority queue discussed in Sect. 7.2.2. An important difference is that the
propensity tree is not sorted; the leaves can be stored in group-number order, and
changes to propensities only result in node values changing rather than the tree
being reordered. Code 7.8 illustrates how the tree is constructed. For the sake of
simplicity, we assume that the number of groups, G, is a power of two, rounding
up and padding with empty groups at the upper end if necessary. The depth of the
tree is log
2
G, requiring 2
depth+1
− 1 nodes. The initial state of the tree is calcu-
lated by storing the group propensity values in the leaves, and then recursively sum-
ming the child values up to the root in the calculatePropensityChildren
method.
On each iteration of SSA-CR, the selection of the group using r
2
a
0
is performed
by working down from the root of the tree. If r
2
a
0
is less than the value in the left

7.3 A Constant Time Method 291
// The tree of cumulative propensity values.
private double[] propensityTree;
// The offset in propensityTree of the first leaf
// -- i.e. propensityTree[propensityTreeLeafOffset] is
// the value for groups[0].
private int propensityTreeLeafOffset;
/**
* Build the tree of cumulative propensity values.
* The sum for all groups will be at the root of the tree.
*/
private void buildPropensityTree()
{
// Calculate how much space is required for the tree,
// storing the group propensity values in its leaves.
int numGroups = groups.size();
int depth = (int) Math.ceil(logBase2(numGroups));
int nodes = (int) (Math.pow(2.0, depth + 1) - 1);
int leaves = (int) Math.pow(2.0, depth);
this.propensityTreeLeafOffset = nodes - leaves;
this.propensityTree = new double[nodes];
// Fill in the leaf values of the tree.
int leafNode = propensityTreeLeafOffset;
for(PropensityGroup group : groups) {
propensityTree[leafNode] =
group.getGroupPropensitySum();
leafNode++;
}
// Pull the leaf values cumulatively up to the root.
calculatePropensityChildren(0);
}
/**
* Sum the child values of node to give the value for node.
* @param node The node to be computed.
* @return The computed value of the node.
*/
private double calculatePropensityChildren(int node)
{
int leftChild = 2 * node + 1;
if(leftChild < propensityTree.length) {
return propensityTree[node] =
calculatePropensityChildren(leftChild) +
calculatePropensityChildren(leftChild + 1);
}
else {
return propensityTree[node]; // Leaf
}
}
Code 7.8 Building the binary tree of cumulative propensity values for SSA-CR

292 7 Simulating Biochemical Systems
child of the root then the left child is descended, otherwise the right child is de-
scended, subtracting the value in the child node from r
2
a
0
. This process is repeated
until a leaf is reached, corresponding to the selected group. The fact that the tree
has depth log
2
G means that this search is typically considerably faster than the un-
optimized linear search illustrated in Code 7.3, and is not directly dependent on the
number of reactions.
7.3.2 Reaction Selection
Selection of a reaction from within the chosen group involves the rejection element
of the algorithm: a reaction is selected and a random propensity generated. Two
random numbers are used for this, r
3
and r
4
in Fig. 7.9. If the random propensity is
larger than the selected reaction’s propensity then that particular reaction is rejected,
and both parts of the selection within the group are repeated until a match is found.
Clearly, it is important to minimize the chance of rejection once a group has been
selected, otherwise reaction selection could take an arbitrary length of time. Min-
imization is achieved by setting the upper limits of group membership to be suc-
cessive powers of 2 times the minimum possible non-zero propensity value (a
min
)
for the set of reactions. When selecting a reaction from within a group, a uniform
random number is generated between zero and the upper boundary of the group.
Because every reaction in the group has a propensity greater than half the up-
per bound, there is a less than a 50% chance that a reaction will be rejected by
the random number, significantly limiting the number of iterations of the rejection
cycle.
3
The number of groups required will be log
2
(a
max
/a
min
), where a
max
is the maxi-
mum possible propensity for the set of reactions. Notice that the number of groups
does not depend on the number of reactions, M, but bounding the number of groups
does depend on being able to calculate the maximum propensity, a
max
. We will dis-
cuss below the potential problems where it is difficult or impossible to determine
a
max
for a set of reactions.
SSA-CR uses the same dependency tree as described in Sect. 7.2 to determine
the impact of reaction selection on other reactions’ propensities. Once a reaction
has been selected, both reaction and group propensities are adjusted accordingly.
The adjustment of a reaction’s propensity may, of course, result in having to move
it from one group to another if its new propensity has crossed either the lower or
upper bound of the group’s range. Because updating the propensity tree is a rela-
tively expensive component of the iteration, the tree update is best done after all the
propensity revisions have been made, rather than as each reaction is adjusted. This
suggests maintaining a record of the changed groups, in the form of a set as part of
the revision step. This will save updating the tree twice for a group if two or more
3
In measurements with our implementation, using a large set of random reactions, the average
number of iterations was around 1.4.
