Барабаш С.Б. Экономико-математические методы и модели
Подождите немного. Документ загружается.

D. Поэтому работа D становится критической, и появляются два новых
критических пути:
кр
P
3
= {A, K, D} и = {A, G, G
кр
P
4
1
, D}.
Продолжим пошаговое сокращение времени выполнения проекта.
Заметим, для того чтобы уменьшить критическое время сетевого графика
еще на один день, теперь недостаточно сократить работу H, так как она не
принадлежит путям и . Поэтому необходимо выбрать иной способ
сокращения. Работа A входит во все критические пути, и удельные затраты
на ее ускорение равны 5 тыс. руб. Остальные способы сокращения
длительностей всех критических путей требуют сокращения одновременно
двух работ, причем удельные затраты на ускорение в этом случае
суммируются.
кр
P
3
кр
P
4
Рассмотрим все возможные варианты, указывая в скобках стоимость
сокращения: K и G (3 + 3 = 6), H и D (2 + 2 = 4), В и D (4 + 2 = 6).
Сравнение их стоимости показывает, что самым дешевым вариантом
является одновременное сокращение работ H и D на один день. Это
приведет к удорожанию стоимости проекта на 4 тыс. руб. и его новая
стоимость будет равна
738 + 4 = 742 (тыс. руб.).
После нового сокращения работы Н работа F становится критической
и появляется еще один критический путь = {F, B}. Сетевой график
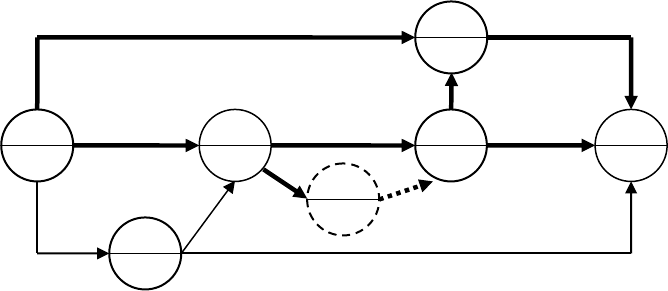
после второго шага сокращения изображен на рис. 4.13.
кр
Р
5
Рис. 4.13. Второй шаг сокращения сетевого графика
Итак, стратегия минимального удорожания комплекса работ при
сокращении сроков строительства на 2 дня (с 44 до 42 дней) состоит в
следующем: необходимо уменьшить продолжительность работы H на
2 дня, а работы D — на 1 день. Ускорение строительства павильона
обойдется в S
уск
= 742 тыс. руб., что на 6 тыс. руб. больше, чем при
нормальном режиме работы:
S
уск
– S =742 – 736 = 6 (тыс. руб.).
При ускоренном строительстве сроком 42 дня сетевой график
проекта будет иметь пять критических путей:
1
0
A
(
18
)
F
(
34
)
C
(
8
)
E
(
32
)
K
(
7
)
D
(
17
)
2
8
3
18
5
25
6
34
7
42
B
(
8
)
Н
(
9
)
4
24
G
(
7
)
L
(
8
)
G
(
0
)
1
кр
P
1
= {A, K, H, B}, = {A, G, G
кр
P
2
1
, H, B},
кр
P
3
= {A, K, D},
к
р
P
4
= {A, G, G
1
, D}, = {F, B}.
кр
Р
5
Задача 5. Построение и анализ уравнения парной линейной регрессии
Воспроизведем еще раз таблицу с исходными данными задачи:
№ 1 2 3 4 5 6 7 8
x
2.82 2.59 2.59 2.58 2.88 3.59 2.44 2.66
y
2.04 1.86 2.26 2.34 2.64 2.59 1.89 2.3
Здесь х = (х
1
,…, х
8
) и у = (у
1
,…, у
8
) — наблюдаемые значения
среднедушевых денежных доходов и потребительских расходов в
субъектах РФ, соответственно.
5.1. Построение математической модели
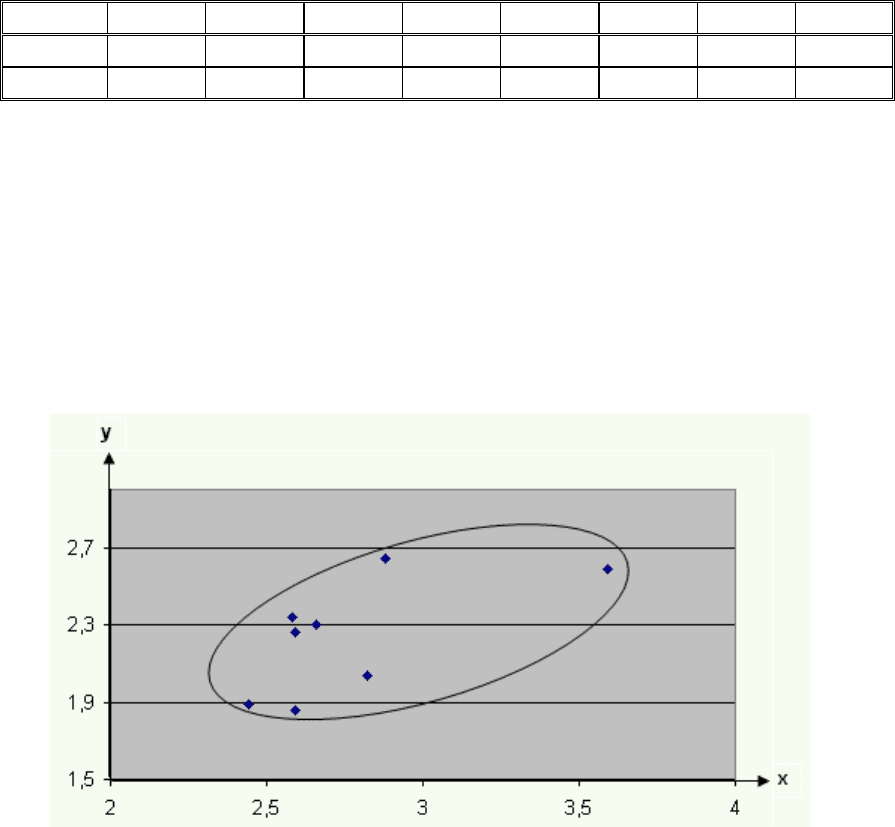
Полем рассеяния называется множество точек на плоскости,
координаты которых соответствуют наблюдаемым значениям
исследуемых показателей. В нашей задаче x
i
— среднедушевые денежные
доходы, y
i
— среднедушевые потребительские расходы в i-м субъекте РФ, i
= 1,…, 8.
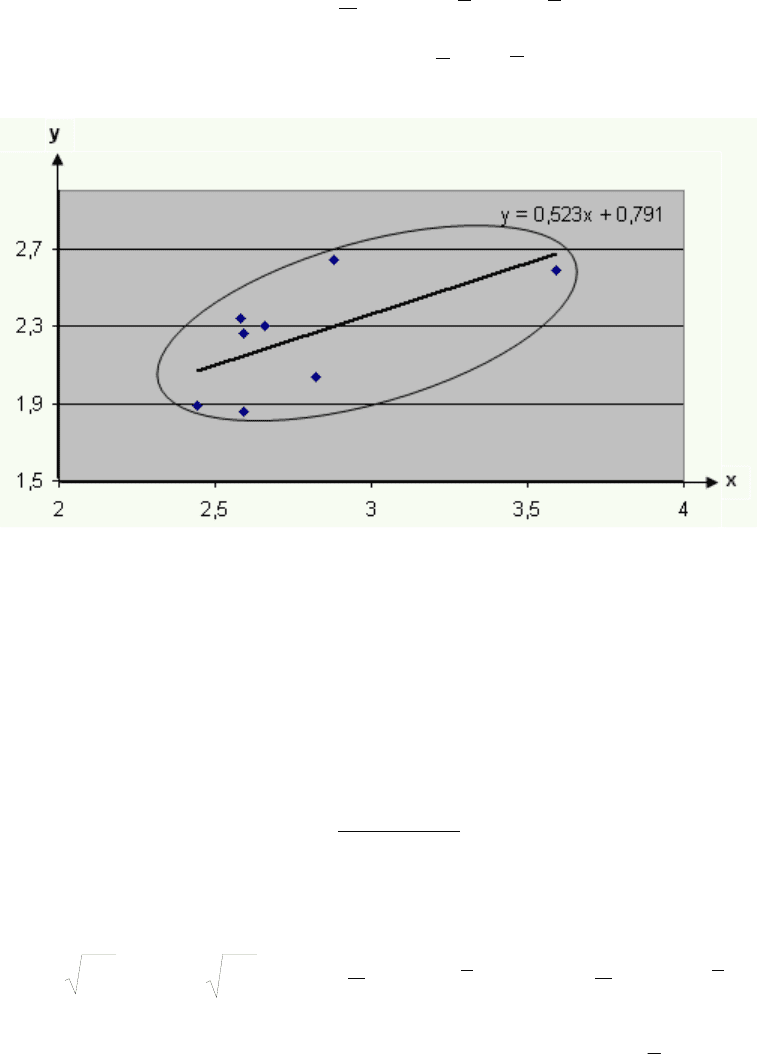
Рис. 5.1. Поле рассеяния наблюдаемых значений доходов и расходов
Визуальный анализ поля рассеяния позволяет выдвинуть гипотезу о
линейной зависимости потребительских расходов y от денежных доходов x
и записать эту зависимость в виде линейной модели
yxu
=
+
+
α
β
,
где
α
и
β
— неизвестные постоянные коэффициенты, а u — случайная
величина, характеризующая отклонения фактических значений расходов
от их теоретических значений
α
+
β
х.
Случайную величину u называют случайным отклонением или
случайным возмущением модели. Ее включение в модель призвано
отразить:
а) влияние не учтенных в модели факторов, влияющих на размер
потребительских расходов;
б) элемент случайности и непредсказуемости человеческих реакций;
в) ошибки наблюдений и измерений.
Отметим также, что переменную х называют независимой или
экзогенной переменной, а переменную y — зависимой или эндогенной.
5.2. Оценка неизвестных параметров модели методом наименьших
квадратов
После формулировки математической модели основная задача
состоит в получении оценок неизвестных параметров
α
и
β
по результатам
наблюдений над переменными x и y, т.е. задача состоит в получении так
называемого уравнения регрессии
ỹ = a + bx,
являющегося некоторой оценкой модели
yxu
=
+
+
α
β
, в котором
коэффициенты a и b есть оценки неизвестных параметров
α
и
β
соответственно. Решение задачи нахождения оценок a и b основывается на
применении метода наименьших квадратов (сокращенно — МНК), суть
которого состоит в следующем.
y
•
•
•
•
•
•
•
•
•
•
•
•
A (x
i
, y
i
)
y
abx=+
B
x
y
i
i
(
,
)
O
x
C (x
i
, 0)
•
•
•
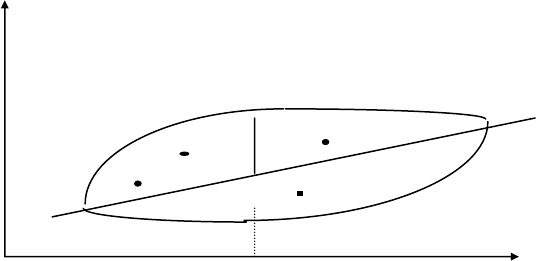
Рис. 5.2. Геометрическая иллюстрация метода наименьших квадратов
Предположим, что для исследуемых экономических показателей x и y
имеется n выборочных наблюдений (х
1
, y
1
), ..., (x
n
, y
n
). На рис. 5.2 в системе
прямоугольных координат нанесено поле рассеяния, точки которого имеют
координаты (x
i
, y
i
), и прямая, соответствующая искомому уравнению
ỹ = a +bx.
Рассмотрим точки A, B, C. Тогда |OC|=x
i
, |AC|=y
i
, |BC|=
y
i
=a+bx
i
.
Отклонение точки A от искомой прямой, измеренное по вертикали, будет
равно . Это отклонение может быть как положительным, так и
отрицательным. Если все отклонения возвести в квадрат и сложить, то
полученная величина будет непосредственно зависеть от разброса точек
iii
yye
~
−=

наблюдения от искомой линии. Различные значения a и b определяют
различные линии, и им будут соответствовать различные суммы квадратов.
Таким образом, сумма квадратов отклонений есть некоторая функция
от a и b, т.е.
∑
=
n
i
i
e
1
2
),()
~
(
22
baFyye
iii
=−≡
∑
∑
.
Метод наименьших квадратов заключается в выборе таких значений
a и b, для которых сумма квадратов
∑
2
i
e
становится минимальной.
Поскольку
∑
∑∑
−−=−≡
222
)()
~
(
iiiii
bxayyye
, то нахождение оценок a
и b
неизвестных параметров
α
и
β
сводится к определению минимума
функции двух переменных F(a, b):
∑
→−−≡ min)(),(
2
ii
bxaybaF
.
Необходимым условием минимума функции двух переменных F(a, b)
является равенство нулю ее первых частных производных
:
⎪
⎩
⎪
⎨
⎧
=−−−=
=−−−=
∑
∑
.x)bxay(
b
)b,a(F
,)bxay(
a
)b,a(F
iii
ii
02
02
∂
∂
∂
∂
После элементарных преобразований эта система сводится к системе
двух линейных уравнений с неизвестными a и b:
⎪
⎩
⎪
⎨
⎧
=+
=+
∑∑∑
∑
∑
.yxxbxa
,yxban
iiii
ii
2
(1)
Систему уравнений (1) называют системой нормальных уравнений.
Используя свойства функции F(a, b) можно показать, что решение системы
(1) является точкой ее минимума. Его можно найти по правилу Крамера:
22
2
)(
∑∑
∑
∑∑∑
−
×−×
=
ii
iiiii
xxn
xyxxy
a
,
22
)(
∑∑
∑
∑
∑
−
−
=
ii
iiii
xxn
yxyxn
b
.
Обозначим через
∑
=
i
x
n
x
1
,
∑
=
i
y
n
y
1
выборочные средние
наблюдаемых значений переменных x и y. Если поделить первое уравнение
системы (1) на n, то получим
∑∑
=+
ii
y
n
x
n
ba
11
или
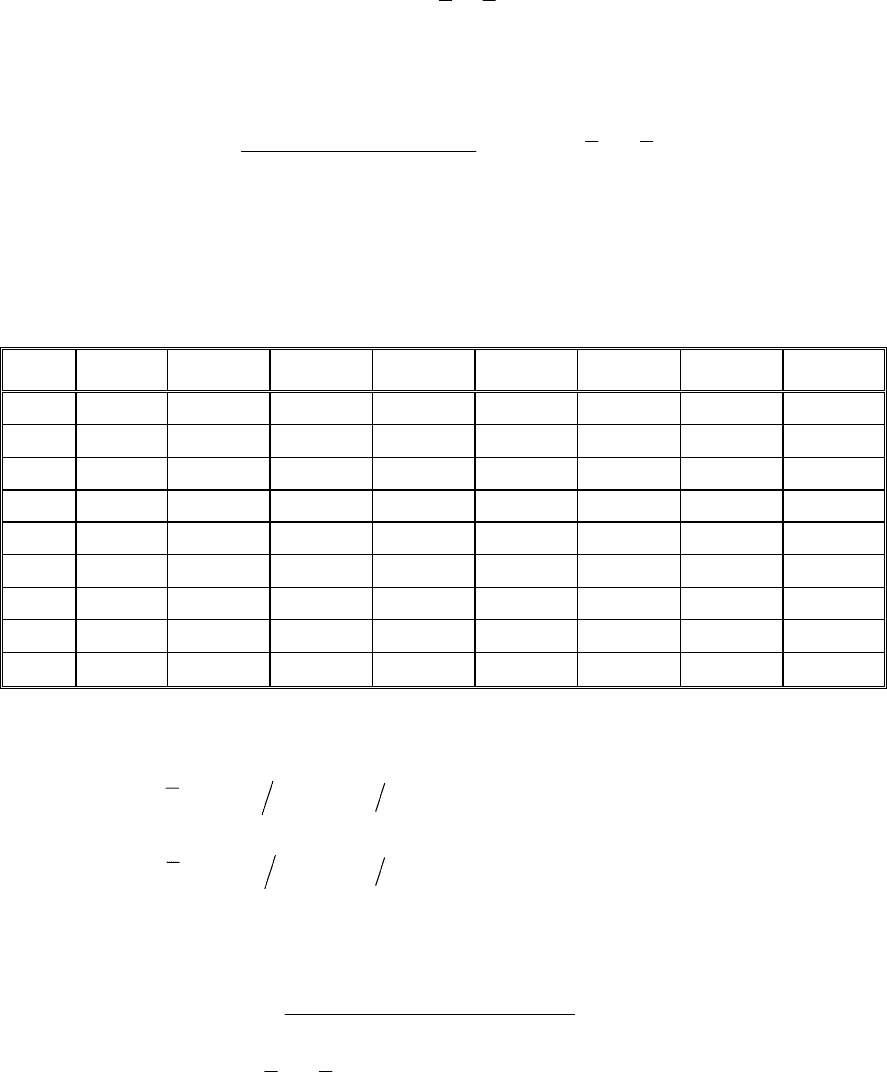
y
x
ba
=
+
.
Таким образом, оценки a и b можно искать по следующим
формулам:
22
)(
∑
∑
∑
∑
∑
−
−
=
ii
iiii
xxn
yxyxn
b
,
x
bya
−
=
, (2)
Для удобства вычисления оценок искомых коэффициентов модели
составляется табл. 1, в которой столбцы «ỹ», «ỹ – y» и «(ỹ – y)
2
»
заполняются после нахождения уравнения регрессии.
Таблица 1
№ x y x
2
xy y
2
ỹ ỹ – y
(ỹ – y)
2
1
2.82 2.04 7.952 5.753 4.162 2.267 0.227 0.051
2
2.59 1.86 6.708 4.817 3.460 2.146 0.286 0.082
3
2.59 2.26 6.708 5.853 5.108 2.146 -0.114 0.013
4
2.58 2.34 6.656 6.037 5.476 2.141 -0.199 0.040
5
2.88 2.64 8.294 7.603 6.970 2.298 -0.342 0.117
6
3.59 2.59 12.888 9.298 6.708 2.670 0.080 0.006
7
2.44 1.89 5.954 4.612 3.572 2.068 0.178 0.032
8
2.66 2.3 7.076 6.118 5.290 2.183 -0.117 0.014
∑
22.15 17.92 62.237 50.09 40.744 0.354
Воспользуемся формулами (2) и значениями последней строки табл. 1
для нахождения оценок a и b. Тогда
77.2815.228
=
=
=
∑
i
xx (тыс. руб.) — среднее значение
среднедушевых доходов;
24.2892.178
=
=
=
∑
i
yy (тыс. руб.) — среднее значение
среднедушевых потребительских расходов.
15.22=
∑
i
x ; ;92.17=
∑
i
y 09.50
=
∑
ii
yx
237.62
2
=
;
∑
i
x
; .
62.490)(
2
=
∑
i
x
Следовательно,
523.0
62.490237.628
92.1715.22092.508
=
−×
×
−
×
=b
;
791.027.2523.024.2
=
×
−
=
−=
x
bya .
Таким образом, искомое уравнение регрессии примет вид
ỹ = 0.791 + 0.523x.
После нахождения уравнения регрессии целесообразно заполнить
столбцы «ỹ», «ỹ – y» и «(ỹ – y)
2
табл. 1. Найденное уравнение регрессии
есть уравнение прямой, которая изображена на рис. 5.3.
5.3. Нахождение коэффициента корреляции
Мерой зависимости между переменными x и y может служить так
называемый выборочный коэффициент ковариации или просто
выборочная ковариация, которая обозначается через COV(x, y) и
определяется по формуле
∑
=
−−=
n
i
ii
yyxx
n
yxCOV
1
))((
1
),(
,
где x
i
, y
i
— выборочные значения, а
x
и
y
— выборочные средние
исследуемых показателей.
Рис. 5.3. График функции регрессии
Эта мера обладает двумя недостатками:
а) ее значение может быть произвольно увеличено в результате
добавления отдельных наблюдений с большими значениями x
i
, y
i
;
б) она может быть произвольно изменена путем выбора единиц
измерения переменных x и y.
Указанных недостатков лишен выборочный коэффициент парной
корреляции, который обозначается через r
xy
и определяется по формуле
yx
xy
SS
yxCOV
r
×
=
),(
, (3)
где S
x
, S
y
— выборочные среднеквадратические отклонения переменных x
и y, определяемые по формулам:
2
xx
SS =
;
2
yy
SS = ;
∑
−=
22
)(
1
xx
n
S
ix
;
∑
−=
22
)(
1
yy
n
S
iy
.
Коэффициент S
x
количественно характеризует меру разброса
выборочных наблюдений x
i
от их среднего значения
x
, причем эта
характеристика имеет ту же размерность, что и переменная x.
Аналогичный смысл имеет коэффициент S
y
.
Формула (3) мало пригодна для практических расчетов. Если
подставить в нее выражения для COV(x, y), S
x
, S
y
и провести некоторые
элементарные преобразования, то получим следующую формулу

∑∑∑∑
∑
∑
∑
−−
−
=
2222
)()(
iiii
iiii
xy
yynxxn
yxyxn
r
. (4)
15.22=
∑
i
x ; ;92.17=
∑
i
y 09.50
=
∑
;
ii
yx
237.62
2
=
∑
i
x
; .
62.490)(
2
=
∑
i
x
Подставляя соответствующие значения из последней строки табл. 1,
получим
642.0
)92.17(744.408)15.22(237.628
92.1715.2209.508
22
≈
−×−×
×
−
×
=
xy
r
.
Коэффициент парной корреляции r
xy
характеризует тесноту линейной
зависимости между x и y. Для коэффициента r
xy
выполняется соотношение
-1 ≤ r
xy
≤ 1. Чем ближе значение |r
xy
| к единице, тем теснее линейная связь
между x и y. Если |r
xy
| = 1, то между x и y существует функциональная
зависимость вида . Если величина |r
bxay +=
xy
| близка к нулю, то это
свидетельствует об отсутствии линейной зависимости между x и y, что не
исключает возможность наличия нелинейной взаимосвязи между x и y.
5.4. Нахождение точечных и интервальных прогнозов
Предположим, что мы хотим распространить нашу модель на другие
значения независимой переменной, отличные от значений x
1
, x
2
, ..., x
n
, т.е.
поставить вопрос о возможности прогнозирования значения зависимой
переменной y, соответствующего некоторому значению независимой
переменной x = x
0
, где x
0
≠ x
i
, i = 1,…, n. Значение x
0
может находиться как
между выборочными наблюдениями от x
1
до x
n
, так и вне
соответствующего интервала.
Прогноз может быть точечным или интервальным. Точечным
прогнозом значения зависимой переменной y, соответствующего
некоторому значению независимой переменной x = x
0
, называется значение
0
~
y
, получаемое путем подстановки в уравнение регрессии x = x
0
, т.е.
000
)(
~
~
bxaxyy
+
=
=
— точечный прогноз.
В реальной экономике точечные прогнозы имеют небольшую
практическую ценность. Для получения прогнозных оценок исследуемого
экономического показателя, которые можно использовать при выработке
практических рекомендаций, используют интервальный прогноз.
Интервальным прогнозом зависимой переменной y, соответствующим
некоторому значению независимой переменной x = x
0
, называется
доверительный интервал, границы которого находятся по формуле
ynНВ
Stxyy
2,210,
)(
~
~
−−
±
=
α
,
где
В
y
~
,
Н
y
~
— соответственно верхняя и нижняя границы доверительного
интервала;

)(
~
0
xy
— точечный прогноз;
221 −− n,
t
α
— квантиль распределения Стьюдента;
(1 –
α
) — доверительная вероятность;
(n – 2) — число степеней свободы;
∑
−
−
+=
2
2
0
)(
)(
1
xx
xx
n
SS
i
y
,
2
SS =
,
2
)
~
(
2
2
−
−∑
=
n
yy
S
ii
.
Доверительный интервал — это такой интервал, в котором с заданной
вероятностью будет находиться прогнозируемое значение зависимой
переменной y. Доверительная вероятность задается извне, т.е. лицом,
проводящем исследование зависимости между x и y. Она характеризует
степень уверенности в справедливости получаемого результата. Чем ближе
к единице значение доверительной вероятности р = (1 –
α
), т.е. чем ближе
к нулю значение
α
, тем с большей уверенностью можно утверждать, что
прогнозируемое значение зависимой переменной y будет находиться в
найденном доверительном интервале. Обычно полагают
α
= 0.1, или
α
= 0.05, или
α
= 0.01.
Следует иметь в виду, что ширина доверительного интервала
существенно зависит от значения (1 –
α
): чем ближе к единице величина (1
–
α
), тем шире доверительный интервал и, следовательно, хуже качество
прогноза. В самом деле, достаточно широкий интервал прогноза не имеет
никакого практического значения. Например, если мы получим результат
типа: «с вероятностью 0.999 среднедушевые среднемесячные расходы в
Томской области в 2009 году будут находиться в пределах от 0 до 10 тыс.
руб.», то от такого результата нет никакой практической пользы, несмотря
на то, что степень его достоверности оценивается в 99.9%.
Поэтому при определении интервального прогноза приходится искать
разумный компромисс между качеством прогноза и его достоверностью,
т.е. шириной доверительного интервала и значением доверительной
вероятности.
Найдем интервальный прогноз среднедушевых среднемесячных
потребительских расходов в Иркутской области, т.е. в 8-м (по таблице
исходных данных) субъекте РФ, в январе-марте 2009 г. в предположении,
что среднедушевые среднемесячные денежные доходы в этом периоде
превысят на 30% соответствующий показатель 2006 г.
Вычислим ожидаемое значение денежных доходов x
0
. Так как
x
8
= 2.66, то x
0
= x
8
+ 0.3x
8
= 2.66 + 0.3×2.66 = 3.458 (тыс. руб.).
Найдем точечный прогноз
0
~
y
:
60.2458.3523.0791.0)(
~
~
00
=
×
+
=
=
xyy
(тыс. руб.).
Пусть
α
= 0.1. Тогда 1-
α
= 0.9;
221 −− n,
t
α
= t
0.95; 6
= 1.943;
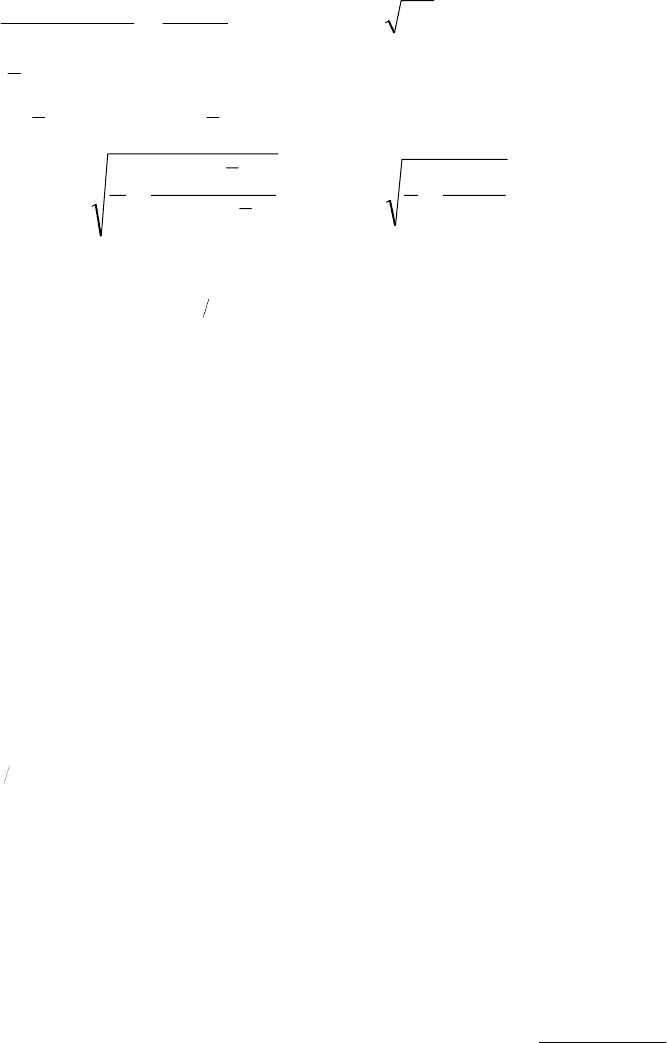
059.0
6
352.0
2
)
~
(
2
2
≈=
−
−∑
=
n
yy
S
ii
;
243.0
2
≈= SS
;
475.0)769.2458.3()(
22
0
≈−=− xx
;
768.2)769.2(8237.62)()(
2222
≈×−=−=−
∑∑
xnxxx
ii
;
Тогда
196.0
768.2
475.0
8
1
243.0
)(
)(
1
2
2
0
~
≈+×=
−
−
+=
∑
xx
xx
n
SS
i
у
.
Следовательно,
38.060.2196.0943.160.2)(
~
~
~
2,210,
±
=
×
±
=
±
=
−− ynНВ
Stxyy
α
,
т.е. (тыс. руб.), а
98.2=
В
y 22.2
=
Н
y
(тыс. руб.).
Это означает, что при увеличении среднедушевых среднемесячных
денежных доходов на 30%, т.е. с 2.66 тыс. руб. до 3.458 тыс. руб., средний
размер среднедушевых среднемесячных потребительских расходов с
вероятностью 0.9 будет колебаться в пределах от 2.22 тыс. руб. до 2.98
тыс. руб. Слова «с вероятностью 0.9» в предыдущем предложении можно
интерпретировать так: «с 90%-й уверенностью можно ожидать, что
средний размер потребительских расходов будет колебаться в пределах от
2.22 тыс. руб. до 2.98 тыс. руб.»
Допустим, мы решили увеличить степень достоверности
интервального прогноза с 90% до 95%. В этом случае 1-
α
= 0.95, т.е.
α
= 0.05. Тогда по таблице квантилей распределения Стьюдента находим
221 −− n,
t
α
= t
0,975; 6
= 2.447 и 48.060.2196.0447.260.2
~
,
±=
×
±
=
НВ
y .
Следовательно,
08.3
~
=
В
y
(тыс. руб.);
12.2
=
Н
y
(тыс. руб.), т.е.
средний размер потребительских расходов будет колебаться от 2.12 тыс.
руб. до 3.08 тыс. руб., и степень достоверности этого результата составляет
95%. В первом случае ширина интервального прогноза составила 2.98 –
2.22 = 0.76 (тыс. руб.), а во втором случае — 3.08 – 2.12 = 0.96 (тыс. руб.).
Таким образом, увеличение степени достоверности с 90% до 95% повлекло
увеличение ширины интервального прогноза на 26%
⎟
⎠
⎞
⎜
⎝
⎛
×
−
%100
76.0
76.096.0
.
Отметим одно важное обстоятельство, которое заключается в том, что
не существует точного правила или формулы, по которым можно задать
«требуемую» в данной конкретной задаче доверительную вероятность. Все
определяется целями исследования. Если степени достоверности прогноза
отдается приоритет по отношению к качеству (ширине интервала
прогноза), то
α
следует выбирать ближе к нулю. В противном случае, т.е.
когда важнее качество прогноза, доверительная вероятность может быть
выбрана на уровне 80-90%.

5.5. Содержательная интерпретация полученных результатов
Рассмотрим найденное уравнение регрессии
x
y 523.0791.0
~
+= .
Коэффициент a = 0.791 не имеет экономического смысла, поскольку
формально соответствует размеру потребительских расходов при нулевом
уровне денежных доходов. Коэффициент b = 0.523 определяет прирост
потребительских расходов, обусловленный приростом денежных доходов.
Действительно, пусть прирост денежных доходов составил Δx.
Определим прирост потребительских расходов Δy:
x
x
x
x
x
y
x
x
yy
Δ
=
+
−
Δ
+
+
=
−
Δ+=Δ 523.0)523.0791.0()(523.0791.0)(
~
)(
~
.
Следовательно,
523.0=
Δ
Δ
x
y
, т.е. прирост денежных доходов, например,
на 100 руб. вызовет прирост потребительских расходов на 52.3 руб.
Содержательная интерпретация всех остальных понятий и формул,
использованных в данной задаче, была приведена по ходу решения.
В заключение выпишем итоговые результаты.
1.
u
x
y
+
+=
β
α
— математическая модель зависимости расходов от
доходов.
2.
x
y 523.0791.0
~
+= — уравнение регрессии, количественно
выражающее зависимость расходов от доходов.
3.
r
xy
= 0.64 — коэффициент корреляции между x и y; его значение
свидетельствует о достаточно тесной линейной зависимости расходов
и доходов.
4.
60.2
~
0
=y
(тыс. руб.) — точечный прогноз;
22.2
~
=
Н
y
(тыс. руб.) интервальный прогноз с 90%-й
98.2
~
=
В
y
(тыс. руб.) доверительной вероятностью;
}
12.2
~
=
Н
y
(тыс. руб.) интервальный прогноз с 95%-й
08.3
~
=
В
y
(тыс. руб.) доверительной вероятностью.
}
ЛИТЕРАТУРА
1. Барабаш С.Б., Воронович Н.В. Экономико-математические методы. —
Новосибирск: НГУЭУ, 2004.
2.
Бахтин А.Е. Математическое моделирование в экономике. —
Новосибирск: НГАЭиУ, 1995.
3.
Бахтин А.Е., Пудова М.В. Математическое моделирование в
экономике. — Новосибирск: НГАЭиУ, 2001.
4.
Доугерти К. Введение в эконометрику. — М: ИНФРА-М, 2001.
