Барабаш С.Б. Экономико-математические методы и модели
Подождите немного. Документ загружается.


где h — любое число, то имеем:
4
2.2766
6
8.81259 tt
−
=
−
.
Отсюда
5036 – 35.2t = 4596 – 13.2t
и, значит, 22t = 440. Таким образом, t
*
= 20.
Итак, из проведенного выше графического анализа следует, что при
10 ≤ t < 20 оптимальным решением задачи (1) – (4) является точка С, а при
20 < t ≤ 40 — точка В. При t = 20 решение определено неоднозначно: им
будет любая точка отрезка [BC].
Теперь мы можем построить функцию спроса S
*
(t) на трудовые
ресурсы.
• При 10 ≤ t < 20 спрос на трудовые ресурсы равен ранее найденной при
t = 10 величине спроса в точке С, т.е. S
*
(t) = S
*
(10) = 2080;
• При 20 < t ≤ 40 спрос на трудовые ресурсы равен ранее найденной при
t = 40 величине спроса в точке В, т.е. S
*
(t) = S
*
(40) = 1280.
• При t = 20 спрос на трудовые ресурсы определен неоднозначно.
В зависимости от того, какое оптимальное решение из отрезка [BC]
будет выбрано, он может принять любое значение из числового
отрезка [1280, 2080], т.е. 1280 ≤ S
*
(t) ≤ 2080.
Зная спрос на трудовые ресурсы, можно определить величину
необходимого кредита V
*
(t) как функцию от ставки труда t, используя
формулу V
*
(t) = t S
*
(t).
• При 10 ≤ t < 20 размер кредита V
*
(t) = t S
*
(t) = 2080t, так как спрос на
трудовые ресурсы не изменяется и равен 2080.
• При 20 < t ≤ 40 размер кредита V
*
(t) = t S
*
(t) = 1280t, так как спрос на
трудовые ресурсы не изменяется и равен 1280.
• При t = 20 размер кредита определен неоднозначно. Так как спрос на
трудовые ресурсы может принять любое значение из отрезка
[1280, 2080], размер кредита V
*
(20) может быть любым числом из
отрезка [1280×20, 2080×20] = [25600, 41600].
Найдем зависимость величины прибыли Р
*
(t) от ставки оплаты труда
t, используя формулу
Р
*
(t) = (1259 – 8.8t) + (766 – 2.2t) ,
*
1
х
*
2
х
где ( , ) — оптимальное решение задачи.
*
1
х
*
2
х
• При 10 ≤ t < 20 оптимальное решение — точка С = (260, 0). Поэтому
величина прибыли Р
*
(t) = (1259 – 8.8t)×260 = 327340 –2288t.
• При 20 < t ≤ 40 оптимальное решение — точка В = (100, 240). Значит
величина прибыли Р
*
(t) = (1259 – 8.8t)×100 + (766 – 2.2t)×240, т.е.
Р
*
(t) = 309740 – 1408t.
• При t = 20 оптимальное решение задачи — любая точка отрезка [BC].
Однако во всех точках этого отрезка величина прибыли одинакова и
равна Р
*
(20) = 309740 – 1408×20 = 281580.
Полученные результаты представлены в табл. 1, а на рис. 2.4 – 2.6
изображены графики функций S
*
(t), PP
*
(t) и V
*
(t).
Таблица 1. Результаты решения задачи
Ставка
оплаты
труда t
(руб.)
Оптимальный
план выпуска
Х
*
(t) = ( , )
x
1
*
x
2
*
Спрос на
трудовые
ресурсы S
*
(t)
(чел.-час)
Размер
кредита V
*
(t)
(руб.)
Величина
прибыли
PP
*
(t)
(руб.)
10 ≤ t < 20 точка С = (260, 0) 2080 2080t 327340 –2288t
t = 20
любая точка
отрезка [В, С]
[1280, 2080] [25600, 41600] 281580
20 < t ≤ 40 точка В = (100, 240) 1280 1280t 309740 – 1408t
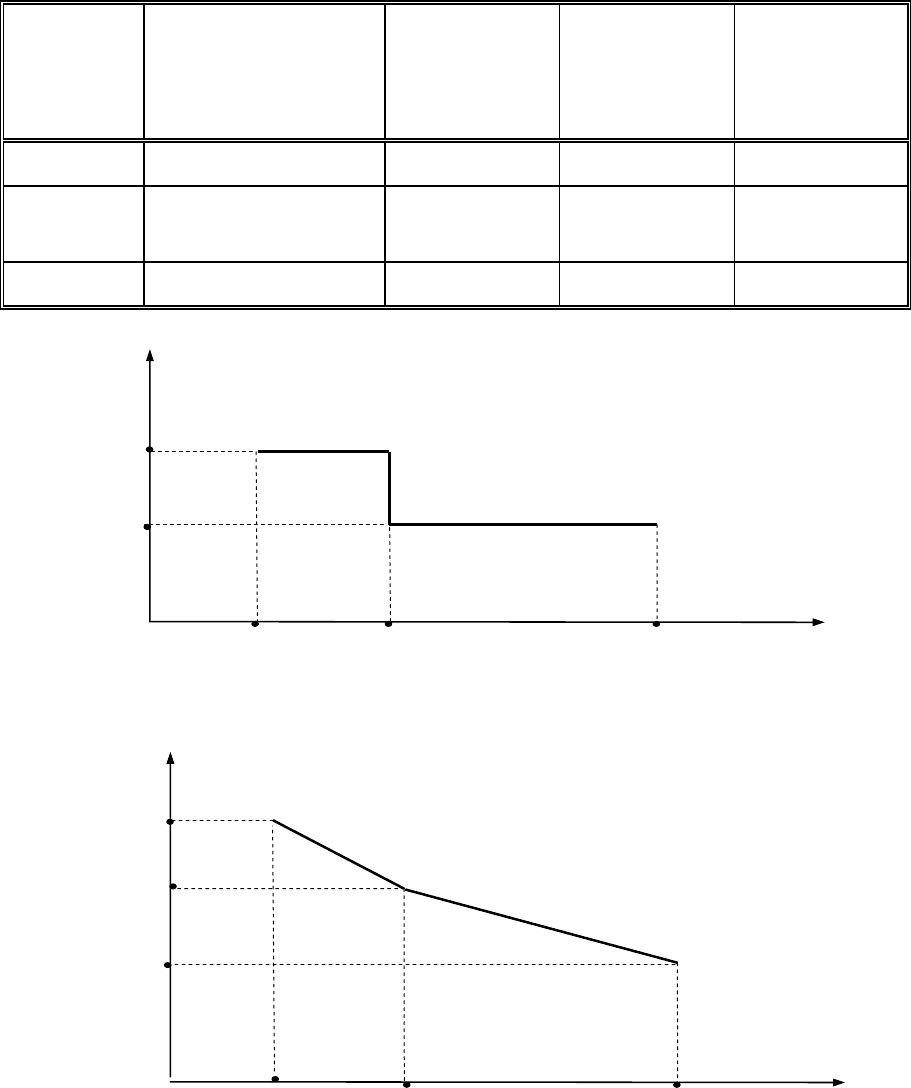
S
*
(t)
0
20
40
t
10
2080
1280
Рис. 2.4. График спроса на трудовые ресурсы
Р
*
(t)
0
t
20 40 10
304460
281580
253420
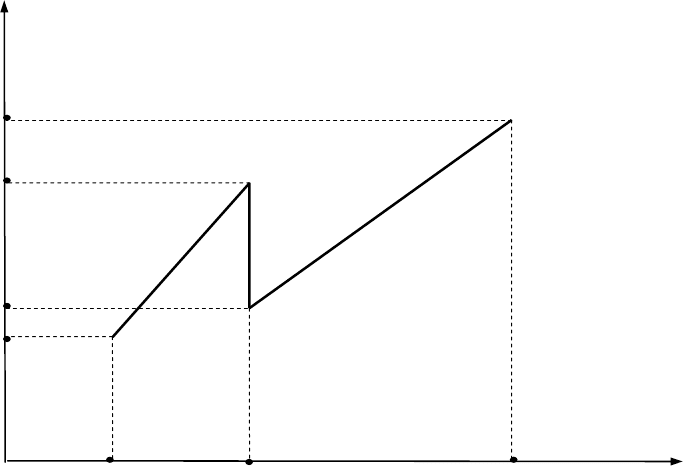
Рис. 2.5. График максимальной прибыли
V
*
(t)
25600
0
20 40
t
10
41600
20800
51200
Рис. 2.6. График потребности в кредите
Замечание 1. Если при t = 10 решением задачи окажется точка В (см.
рис. 2.1), то возможны две ситуации:
1. вектор grad P(T) проходит выше grad P(10),
2. вектор grad P(T) проходит ниже grad P(10.
В первом случае при увеличении параметра t от 10 до Т вектор grad P(t)
поворачивается против часовой стрелки, как в рассмотренной выше задаче.
Поэтому при некотором значении t = t
*
оптимальными решениями будут все
точки отрезка [АВ], а затем – точка А.
Во втором случае при увеличении параметра t от 10 до Т вектор grad P(t)
поворачивается по часовой стрелке. Поэтому при некотором значении параметра
t = t
*
оптимальными решениями задачи будут все точки отрезка [ВС], а затем –
точка С.
Если оказалось, что t
*
> Т, то это означает, что при изменении ставки труда
t в интервале [10, Т] оптимальное решение не изменяется. Но такая ситуация
встретиться в контрольной работе не должна.
Замечание 2. Графический метод не всегда позволяет правильно
определить оптимальное решение задачи, особенно в тех случаях, когда чертеж
выполнен не очень аккуратно. Известно, что решение задачи линейного
программирования всегда является одной из вершин многоугольника
допустимых решений. Поэтому, если нет полной уверенности в том, что
графически оптимальное решение найдено правильно, целесообразно вычислить
значения целевой функции в соседних вершинах многоугольника допустимых
решений и сравнить с найденным «оптимальным» значением целевой функции.
Они не должны быть больше этого значения.

Косвенным свидетельством того, что задача решена неверно, является
неравенство: S
*
(10) < S
*
(Т), которое означает, что потребность в рабочей силе
увеличивается с ростом ставки труда. На самом деле всегда должно выполняться
противоположное неравенство: S
*
(10) ≥ S
*
(Т).
Задача 3. Задача максимизации объема выпускаемой продукции в
условиях ограниченных финансовых ресурсов
1) Производственная функция (ПФ) — функция, описывающая
зависимость максимального объема производимого продукта от затрат
ресурсов (факторов), используемых в производственном процессе. В
задаче в качестве ресурсов выступают рабочая сила (L, тыс. чел.-час.) и
оборудование (K, тыс. ст.-час.). Производственная функция фирмы,
построенная путем обработки статистических данных, имеет вид:
,LKY
.. 3020
25=
где Y — объем выпуска продукции (ед.).
Построим графики производственной функции при фиксированном
значении одной из переменных.
а) Пусть K = 20. Тогда ПФ — степенная функция следующего вида:
Y =
.L.L
... 303020
5452025 ≈⋅
Вычислим значения этой функции в двух точках, например, L = 9 и
L = 27. Имеем, что Y(20, 9) = 88.96, а Y(20, 27) = 122.3. График функции
представлен на рис. 3.1(а).
б) Пусть L = 18. Тогда ПФ — степенная функция следующего вида:
Y =
.К.К
... 203020
5591825 ≈
Также вычислим значения этой функции в двух точках, например K =
6 и K = 35. Имеем, что Y(6, 18) = 85.14, а Y(35, 18) = 121.15. График
функции представлен на рис. 3.1(б).
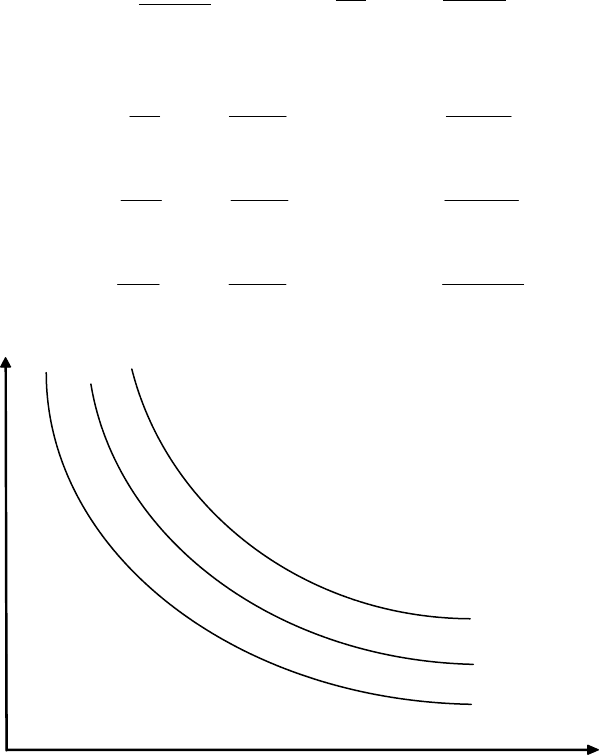
122.3
88.96
121.15
85.14
(а) (б)
6 35
К
Y
0
Y
20
559
.
К.=
Y
Y
30
545
.
L.
=
9 27
L
0
Рис. 3.1. Графики производственной функции при фиксированном
значении одной из переменных
Отметим, что заданная ПФ удовлетворяет основным свойствам
производственных функций:
• при отсутствии хотя бы одного ресурса объем выпуска продукции
равен нулю, то есть Y(0, 0) = Y(K, 0) = Y(0, L) = 0;
• с ростом затрат хотя бы одного ресурса объем выпуска Y растет;
• с ростом затрат одного ресурса при неизменном количестве другого
величина прироста выпуска на каждую дополнительную единицу
увеличивающегося ресурса убывает, т.е. имеет место закон
убывающей эффективности ресурсов.
2) Изокванта — совокупность всех комбинаций факторов
производства (K, L), обеспечивающих одинаковый объем выпускаемой
продукции. Изокванты дают графическое представление двухфакторной
производственной функции Y(K, L) в виде ее линий уровня.
Выпишем соответствующие этим значениям уравнения изоквант:
Y
= = 69;
3020
25
..
LК
Y = 103;
3020
25
..
LК=
Y = = 137.
3020
25
..
LК
Для построения на плоскости OKL изоквант целесообразно из их
уравнений в явном виде выразить переменную L как функцию от
переменной K:
20
30
25
.
.
K
Y
L =
или
32
310
1
25
/
/
K
Y
L ⋅
⎟
⎠
⎞
⎜
⎝
⎛
=
.
Итак, уравнения трех изоквант запишем в следующем виде:
3/2
3/10
1
25
69
K
L ⋅
⎟
⎠
⎞
⎜
⎝
⎛
=
, отсюда
3/2
49.29
K
L = ;
3/2
3/10
1
25
103
K
L ⋅
⎟
⎠
⎞
⎜
⎝
⎛
=
, отсюда
3/2
11.112
K
L = ;
3/2
3/10
1
25
137
K
L ⋅
⎟
⎠
⎞
⎜
⎝
⎛
=
, отсюда
3/2
14.290
K
L = .
L
0
K
B B
Y
B
1
B = 69
Y
3
= 137
Y
2
= 103
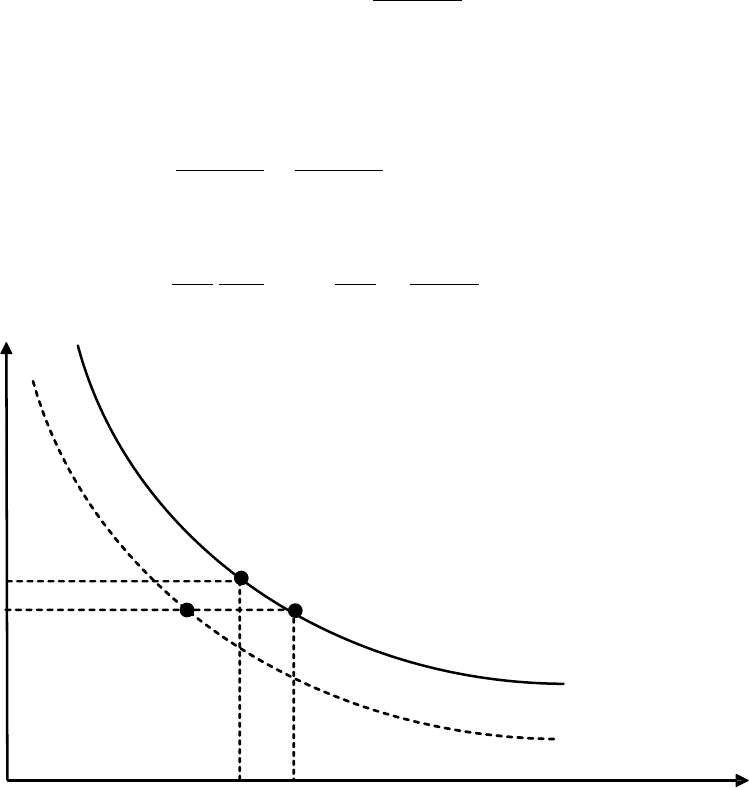
Рис. 3.2. Изокванты производственной функции
3) Известны объем выпуска продукции Y
баз
= 102 (ед.) и наличные
трудовые ресурсы L
баз
= 20 (тыс. чел.-час.) в базовом периоде. Определим
потребность в оборудовании в плановом периоде при увеличении объема
выпуска продукции на 10%, если возможность увеличения трудовых
ресурсов составляет не более 5%.
При заданном увеличении объем выпуска продукции составит
Y = 1.1⋅Y
баз
= 1.1⋅102 = 112.2 (ед.).
Существует множество комбинаций факторов производства (K, L),
обеспечивающих выпуск продукции в объеме 112,2 ед. Потребность в
оборудовании в плановом периоде можно выразить как функцию от
объема трудовых ресурсов. Используя уравнение изокванты
211225
3020
.LКY
..
== ,
имеем:
23
811820
/
L
.
K =
.
Таким образом, если объем трудовых ресурсов, используемых в
производстве, не изменится и останется на уровне L
баз
=20 (тыс.чел.-час.),
то потребность в оборудовании в плановом периоде составит
35720
20
811820811820
2323
.
.
L
.
K
//
≈==
(тыс. ст.-час.).
В базовом периоде потребность в оборудовании составляла
6412
20
1
25
1021
25
102
23
55
30
.
L
K
/.
≈
⎟
⎠
⎞
⎜
⎝
⎛
=
⎟
⎠
⎞
⎜
⎝
⎛
= (тыс. ст.-час.).
K
L
0
(18,921; 21)
(12,64; 20)
(20,357; 20)
Y = 112,2
Y = 102

Рис. 3.3. Потребность в ресурсах в плановом периоде
Если же объем трудовых ресурсов увеличится на 5% по отношению к
базовому и составит
L = 1.05⋅L
баз
= 1.05⋅20 = 21 (тыс. чел.-час.),
то потребность в оборудовании в плановом периоде составит
92118
21
811820811820
2323
.
.
L
.
K
//
≈==
(тыс. ст.-час.).
Итак, при объеме трудовых ресурсов
[
]
базбаз
L.;LL 051
∈
потребность
в оборудовании в плановом периоде составит некоторую величину
, определяемую соотношением
[
3572092118 .;.K ∈
]
23
811820
/
L
.
K =
.
На рис. 3.3 изображена изокванта ПФ уровня Y = 112.2 и отмечены
комбинации факторов производства (20.357; 20) и (18.921; 21),
обеспечивающие выпуск продукции в объеме 112.2 ед.
4) Согласно условию фирма может приобрести на рынке
используемые в производстве ресурсы по ценам p
K
= 14 (ден. ед. / тыс. ст.-
час.) и p
L
= 8 (ден. ед. / тыс. чел.-час.). Величина ее затрат C на покупку L
единиц рабочей силы и К единиц оборудования составит
С
= p
K
К + p
L
L = 14К + 8L.
Задача фирмы состоит в нахождении максимального объема выпуска
продукции при условии, что уровень затрат на покупку ресурсов не
превосходит 560 ден. ед. Математическая модель этой задачи может быть
записана так: найти объемы ресурсов К и L, удовлетворяющие
ограничениям
14К + 8L ≤ 560, (1)
К ≥ 0, L ≥ 0 (2)
и доставляющие максимальное значение целевой функции
Y = 25K
0.2
L
0.3
→ max. (3)
Так как Y — нелинейная функция, то эта модель представляет собой
задачу нелинейного программирования. Ограничение (1) называется
бюджетным ограничением.
Ее решение можно найти графическим методом. Для этого построим
область допустимых решений, задаваемую условиями (1) и (2). Она
представляет собой заштрихованный треугольник ОАВ (см. рис. 3.4).
Граничная прямая АВ бюджетного ограничения задается уравнением

14K + 8L = 560.
Для определения оптимального решения проведем несколько линий
уровня (изоквант) целевой функции, имеющих общие точки с областью
допустимых решений. Как было показано в п. 2, чем выше находится
изокванта, тем большему уровню целевой функции она соответствует (Y
2
> Y
1
) (см. рис. 3.4). Поэтому изокванта, соответствующая максимально
возможному объему выпуска, должна касаться граничной прямой
бюджетного ограничения (1), а точка ее касания D будет оптимальным
решением задачи.
Рис. 3.4. Графическое решение задачи производителя
Для нахождения значений координат точки D используем тот факт,
что градиент целевой функции grad Y =
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
L
Y
,
K
Y
, вычисленный в точке
касания, перпендикулярен прямой АВ. Это означает, что вектор grad Y и
вектор нормали ОС = (p
K
, p
L
) этой прямой пропорциональны, т.е.
справедливо равенство
LK
pp
L
Y
K
Y
=
∂
∂
∂
∂
. (4)
Поскольку
,
K
.
L.
L
K
.
LK.
L
Y
K
Y
..
..
⋅
⋅
=
⋅
⋅
=
∂
∂
∂
∂
−
−
30
20
2530
2520
7020
3080
отсюда имеем, что
.
p
p
K.
L.
L
K
4
7
8
14
30
20
===
⋅
⋅
Следовательно, 21K = 8L или K = (8/21)L. Подставляя полученное
выражение K через L в уравнение граничной прямой АВ, получаем:
8L + 14(8/21)L = 560 или (40/3)L = 560.
Y = Y
1
K
L
14K + 8L = 560
И
зокоста
A
B
14
D = (K
*
, L
*
)
О
8
40 16
42
70
C = (p
К
, р
L
)
Точка рыночного равновесия
фирмы
Y = Y
2
Y = Y
*
= 133.58
И
зокванта
grad Y =
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
∂
∂
L
Y
,
K
Y

Отсюда имеем, что оптимальная величина трудовых ресурсов равна
L
*
= 3·560/40 = 42.
Оптимальный объем оборудования равен
K
*
= (8/21)L = (8/21)42 = 16,
а соответствующий объем выпуска Y
*
= 25·16
0.2
·42
0.3
≈ 133.58.
Граничная прямая ограничения (1) является линией уровня функции
издержек фирмы C(K, L) = 14K + 8L и называется изокостой. Таким
образом, оптимальное решение (K
*
, L
*
) задачи фирмы геометрически
представляет собой точку касания изокванты и изокосты. Эта точка
называется точкой рыночного равновесия фирмы.
Частная производная
K
Y
∂
∂
в формуле (4) — это предельная
производительность оборудования. Она показывает, на сколько единиц
увеличится объем выпуска продукции, если объем затрат оборудования
увеличится на одну (малую) единицу, а затраты рабочей силы останутся на
прежнем уровне. Соответственно, частная производная
L
Y
∂
∂
— это
предельная производительность рабочей силы. Само равенство (4)
означает, что в точке рыночного равновесия отношение предельных
производительностей ресурсов равно отношению их цен.
Отношение предельных производительностей оборудования и
рабочей силы называется предельной нормой технологического замещения
оборудования рабочей силой и обозначается MRTS
KL
. Эта величина
показывает, на сколько единиц нужно увеличить затраты рабочей силы,
чтобы при уменьшении затрат оборудования на одну единицу объем
выпуска продукции остался на прежнем (оптимальном) уровне. Таким
образом, предельная норма технологического замещения оборудования
рабочей силой в точке рыночного равновесия равна отношению цен этих
ресурсов, т.е.
751814 .ppMRTS
LKKL
=
=
=
.
Равенство (4) можно записать иначе:
LK
p
L
Y
p
K
Y
∂
∂
=
∂
∂
. (5)
Равенство (5) означает, что в точке равновесия отношения предельных
производительностей ресурсов к их рыночным ценам равны между собой.
Величину этого отношения можно интерпретировать как предельную
эффективность финансовых ресурсов
С
Y
∂
∂
. Она показывает, на сколько

увеличится выпуск продукции Y, если увеличить объем капитала С,
затрачиваемого на ресурсы, на 1 ден. ед. В нашей задаче предельная
эффективность финансовых ресурсов
С
Y
∂
∂
=
K
p
K
Y
∂
∂
= (0.2·25·16
-0.8
·42
0.3
)/14
≈ 0.12,
что означает следующее: при увеличении затрат на 1 ден. ед. объем
выпускаемой продукции возрастет на 0.12 ед.
Итак, получены следующие результаты.
1.
Фирма должна взять в аренду K
*
= 16 тыс. ст.-час. оборудования и
нанять по контракту L
*
= 42 тыс. чел.-час. рабочей силы. В этом
случае при имеющемся бюджетном ограничении будет выпущено
максимальное количество продукции Y
*
= 133.58 ед.
2.
Предельная норма технологического замещения оборудования
рабочей силой MRTS
KL
= 1.75.
3.
Предельная эффективность финансовых ресурсов равна 0.12.
Задача 4. Построение и анализ сетевых графиков. Оптимизация
сетевого графика
Сетевая модель представляет собой план выполнения некоторого
комплекса взаимосвязанных работ, заданный в специфической форме сети,
графическое изображение которой называют сетевым графиком.
Главными элементами сетевой модели являются события и работы.
Событие — это момент достижения некоторого результата. Событие не
имеет протяженности во времени. Понятие «работа» может иметь разный
смысл и обозначать:
• действительную работу, требующую затрат времени и ресурсов;
• ожидание, не требующее затрат ресурсов, но занимающее
определенное время;
• фиктивную работу, которая вводится для отображения логической
связи между событиями, не требует затрат ресурсов и не имеет
продолжительности во времени.
Для каждой работы сетевой модели должны быть определены такие
работы, на результаты которых она непосредственно опирается и которые
должны быть завершены к моменту начала ее выполнения.
Среди событий сетевой модели выделяют начальное,
промежуточные и конечное. Начальное событие не имеет
предшествующих работ, а конечное — последующих работ. У
промежуточных событий есть и предшествующие, и последующие работы.
