Baez J.C. (Ed.) Knots and Quantum Gravity (Oxford Lecture Series in Mathematics and Its Applications)

Подождите немного. Документ загружается.

BF Theories and 2-knots 189

22. J. S. Carter and M. Saito, Reidemeister moves for surface isotopies

and their interpretation as moves to movies, J. Knot Theory Rami-

ﬁcations, 2 (1993) 251–28 4.

23. D. Roseman, Reidemeis ter-type moves for surfaces in four-

dimensional space, preprint (1992).

24. J. S. Carter and M. Saito, Knotted s urfaces, braid movies, and be-

yond, this volume.

25. J. E. Fischer, Jr, Geometry of 2-categories, PhD Thesis, Yale Uni-

versity (1993).

26. A. B. Zamolodchikov, Tetrahedra equations and integrable systems

in 3-dimensional space, Sov. Phys. JETP 52 (1980) 32 5–336.

27. P. Cotta-Ramusino, E. Guadagnini, M. Martellini, and M.

Mintchev, Quantum ﬁeld theory and link invariants, Nucl. Phys.

B330 (1 990) 557–574 .

28. J. S. Carter and M. Saito, On formulations and s olutions of simplex

equations, preprint (1992).

29. R. J. Lawrence, Algebras and triangle relations, preprint (1992).

190 Paolo Cotta-Ramusino and Maurizio Martellini

Knotted Surfaces, Braid Movies, and Beyond

J. Scott Carter

Department of Mathematics, University of South Alabama,

Mobile, Alabama 36688, USA

(email: carter@mathstat.usouthal.edu)

Masahico Saito

Department of Mathematics, University of Texas at Austin,

Austin, Texas 78712, USA

(email: saito@math.utexas.edu)

Abstract

Knotted surfaces embedded in 4-space can be visualized by means

of a variety of diagrammatic methods. We review recent develop-

ments in this direction. In particular, generalizations of b raids are

explained. We discuss generalizations of the Yang–Baxter equation

that correspond to diagrams appearing in the study of knotted sur-

faces. Our diagrammatic methods of producing new solutions to

these generalizations are reviewed. We observe 2-categorical aspects

of these diagrammatic methods. Finally, we present new observa-

tions on algebraic/algebraic-topological aspects of these approaches.

In particular, they are related to identities among relations that ap-

pear in combinatorial group theory, and cy cles in Cayley complexes.

We propose generalizations of these concepts from braid groups to

groups that have certain types of Wirtinger presentations.

1 Introduction

It ha s been hoped that ideas from physics can be use d to generalize quan-

tum invariants to higher-dimensional knots and manifolds. Such possibili-

ties were discussed in this conference.

In dimension 3 Jones-type invariants were deﬁned algebraically via braid

group representations or diagrammatically via Kauﬀman brackets. The

ﬁrst step, then, in the 1-dimensionally higher case is to get algebraic or

diagrammatic ways to describe knotted surfaces embedded in 4-space.

In this paper, we ﬁrst re view recent developments in this direction.

Reidemeister-type moves were generalized by Roseman [38] and their movie

versions were clas siﬁed by the authors [4, 7]. On the other hand, various

braid forms for surfaces were considered by several other authors. In partic-

ular, Kamada [26] proved generalized Alexander’s and Markov’s theorems

for surfa c e braids deﬁned by Viro. We combined the movie and the surface

braid approaches to obtain moves for the braid movie form of knotted sur-

191

192 J. Scott Carter and Masahico Saito

faces. The braid movie description is rich in algebraic and diagrammatic

ﬂavor.

The exposition in Section 2 provides the basic topological to ols for ﬁnd-

ing new invariants along these lines if they exist.

On the other hand, knot theoretical, diagrammatic techniques have

been used to solve algebraic problems related to statistical physics. In par-

ticular, we gave solutions to various types of generalizations of the quan-

tum Yang–Baxter equation (QYBE). Such generalizations originated in

the work of Zamo lodchikov [43]. In Section 3 we review our diagrammatic

methods in solving these equations.

Such generalizations appeared in the context o f 2-categories [27] and

higher algebraic structures [33]. In Section 4 we follow Fischer [14] to show

that braid movies form a braided monoidal 2-category in a natural way.

New obser vations in this paper are in Section 5, where we discus s close

relations between braid movie moves and various concepts in alg e bra and

algebraic topology. Some of the moves correspond to 2-cycles in Cayley

complexes. Others are related to Peiﬀer equivalences that are studied in

combinatorial group theory and homotopy theory. The charts deﬁned in

Section 2 can be regarded as ‘pictures’ (that a re deﬁned for any group

presentations) of null homotopy disks in classifying spaces. We pr op ose

generalized chart moves for groups that have Wirtinger presentations.

2 Movies, surface braids, charts, and isotopies

2.1 Movie moves

The motion picture method for studying knotted surfaces is o ne of the most

well known. It originated with Fox [15] and has been developed and used

extensively (for example [15, 23, 29, 30, 36]). In [4, 7] we gave a set of

Reidemeister moves for movies of knotted surfaces such that two movies

described isotopic knottings if and only if one could be obtained fro m the

other by means of certain local changes in the movies. In order to depict

the movie moves, we ﬁrst projected a knot onto a 3-dimensional subspace

of 4-space.

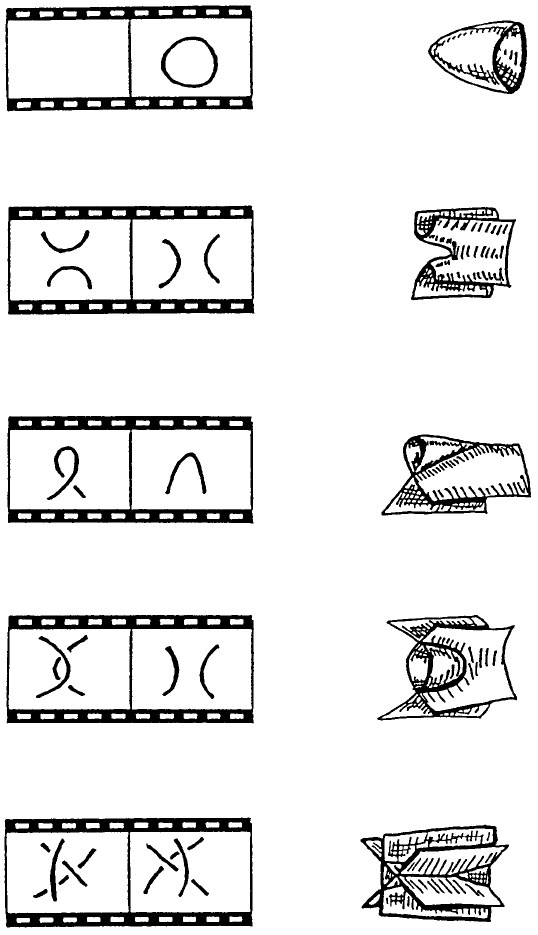
Here a map from a surface to 3-space is called generic if every po int

has a neighborhood in which the surface is either (1) embedded, (2) two

planes intersecting along a double-point curve, (3 ) three planes intersecting

at an isolated triple point, or (4) the cone on the ﬁgure eight (also called

Whitney’s umbrella). Such a map is called generic because the collection

of maps of this form is an open dense subset of the space of all the smooth

maps; see [18]. Local pictures of these are depicted in Fig. 1.

Then we ﬁx a height function on the 3-space . By cutting 3- space by

level planes, we get immersed circles (with ﬁnitely many exceptions where

critical p oints occur). We also can include crossing information by br e ak-

ing circles at underpasses. By a movie we mean a sequence of such curves

Knotted S urfaces, Braid Movies, and Beyond 193

Fig. 1. Generic intersection points

194 J. Scott Carter and Masahico Saito

on the planes. Each element in a sequence is called a still. Again without

loss of generality we can assume that s ucc e ssive stills diﬀer by at most a

classical Reidemeister move or a critical point of the surface. The Reide-

meister moves are interpreted as critical points of the double points of the

projected surface, and so the movies contain critical information for the

surface and for the projection of the surface. Finally, the moves to these

movies were classiﬁed following Roseman [38] by means of an analysis of

fold-type singularities and intersection sets.

The movie moves are depicted in Figs 3 and 4. In these ﬁg ures each still

represents a local picture in a larger knot diagram. The diﬀerent stills diﬀer

by either a Reidemeister move or critical point (birth/death or saddle) on

the surface. These are called the elementary string interactions (ESIs).

Figure 2 depicts ESIs. The moves indicate when two diﬀerent sequences

of ESIs depict the same knotting. Any two movie descriptions of the same

knot are related by a sequence of these moves. One rather large class of

moves is not explicitly given in this list: na mely, distant ESIs commute;

that is, when two string interactions occur on widely separated se gments,

the order of the interactions can be switched.

2.2 Surface braids

In April 1992, Oleg Viro described to us the bra ided form of a knotted

surface. Similar notions had been considered by Lee Rudolph [39] and X.

S. Lin [35]. Kamada [22- 26] has studied Viro’s version of surface braids;

we follow Kamada’s descriptions.

2.2.1 Deﬁnitions

Let B

and D

denote 2-disks. A surface braid is a compact oriented surface

F properly embedded in B

× D

such that

(1) the projection p: B

×D

→ D

to the second factor restricted to F ,

: F → D

, is a branched covering;

(2) The boundary of F is the s tandard unlink: ∂F = (n points) ×∂D

⊂

× ∂D

⊂ ∂(B

× D

) where n points are ﬁxed in the interior of

Here the positive integer n is called the (surface) braid index. A surface

braid is called simple if every branch point has branch index 2. A surface

braid is simple if the covering in condition (1) above is simple. Throughout

the paper we consider simple sur face braids only.

Two surface braids ar e equivalent if they are isotopic under level-

preserving isotopy relative to the boundary, wher e we regard the projection

p: B

× D

→ D

as a disk bundle over a disk.

2.2.2 Closed surface braids

Let F ⊂ B

× D

be a sur fa c e braid with braid index n. Embed B

× D

in 4- space standardly. Then ∂F is the unlink in the 3-sphere ∂(B

× D

)

Knotted S urfaces, Braid Movies, and Beyond 195

Fig. 2. The elementary string interactions

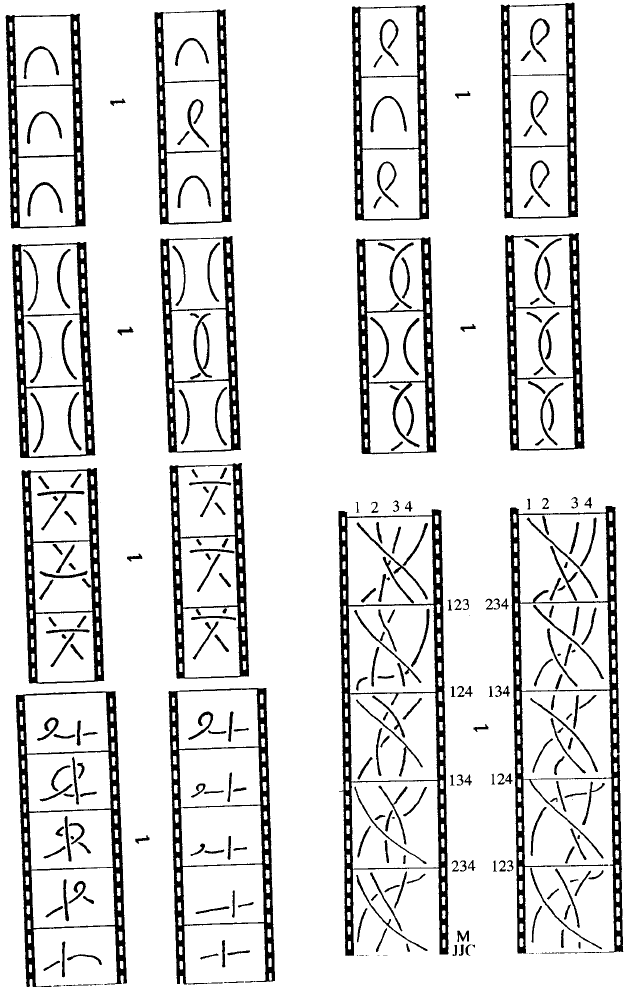
196 J. Scott Carter and Masahico Saito

Fig. 3. The Roseman moves

Knotted S urfaces, Braid Movies, and Beyond 197

Fig. 4. The remaining movie moves

198 J. Scott Carter and Masahico Saito

so that we can cap oﬀ these circles with the s tandard embedded 2-disks in

4-space to obtain a closed, orientable embedded surface in 4-space. The

closed surface,

F (called the closure of F ), is deﬁned up to ambient isotopy.

A surface obtained this way is called a closed surface braid.

Viro a nd Kamada [23] have proven an Alexander theorem for surfaces.

Thus, any orientable surface embedded in R

is isotopic to a closed surface

braid. Furthermore, Ka mada [26] has recently proven a Markov theorem

for closed surface braids in the PL category. However, in his proof he does

not assume that the bra nch points are simple. An open problem, then, is

to ﬁnd a proof of the Markov theorem for closed surface bra ids in which

each branch point is simple. Such a theorem would show a clear analogy

between classical and higher-dimensional knot theory.

2.2.3 Braid movies

Write B

and D

as products of closed unit intervals: B

= B

× B

= D

×D

. Factor the projection p: B

×D

→ D

into two pr ojections

: B

× B

× D

→ B

× D

and p

: B

× D

→ D

Let F be a surfac e braid. We may assume without loss of genera lity

that p

restricted to F is generic. We further regard the D

factor in

× D

= B

× D

as the time direction. In other words, we

consider families {P

= B

× D

× {t} : t ∈ D

}. Except for a ﬁnite

number of va lues of t ∈ D

the intersection p

(F ) ∩ P

is a collection of

properly immersed curves on the disk P

Exceptions occur when P

passes through branch points, o r local max-

ima/minima of the double-point set, or triple points. We may assume that

for a ny t ∈ D

there exists a pos itive  such that at most only one of such

points is contained in ∪

s∈(t−,t+)

. If one of such points is contained,

the diﬀerence between p

(F ) ∩ P

, s = t ± , is one of the following: (1)

smoothing/unsmoothing of a crossing (corresponding to a branch point),

(2) type II Reidemeister move (corresponding to the maximum/minimum

of the double-point set), or (3) type III Reidemeister move (corresponding

to a triple po int).

Except for such t, p

(F ) ∩P

is the projection o f a classical br aid. Fur-

thermore, we can include cro ssing informatio n by breaking the under-arc as

in the classical case. Here the under-arc lies below the over-arc with respect

to the projection p

. To make this convention more precise we identify the

image of p

with an appropriate subset in B

×D

. This idea was used by

Kamada when he constructed a surface with a given chart. See [22] and

also the next section.

By this convention we can describe s urface braids by a sequence of

classical braid words. Including another braid group relation (σ

= σ

|i − j| > 1) we deﬁne a braid movie as follows.

A braid movie is a sequence (b

, . . . , b

) of words in σ

±1

, i = 1, . . . , n,

such that for any m, b

m+1

is obtained from b

by one of the following