Baez J.C. (Ed.) Knots and Quantum Gravity (Oxford Lecture Series in Mathematics and Its Applications)

Подождите немного. Документ загружается.

Knotted Surfaces, Braid Movies, and Beyond 199

changes:

(1) inse rtion/deletion of σ



(2) inse rtion/deletion of a pair σ



−

(3) replacement of σ



by σ



where |i − j| > 1,

(4) replacement of σ



by σ



where |i − j| = 1.

These changes ar e called elementary braid changes (or E BCs, for short).

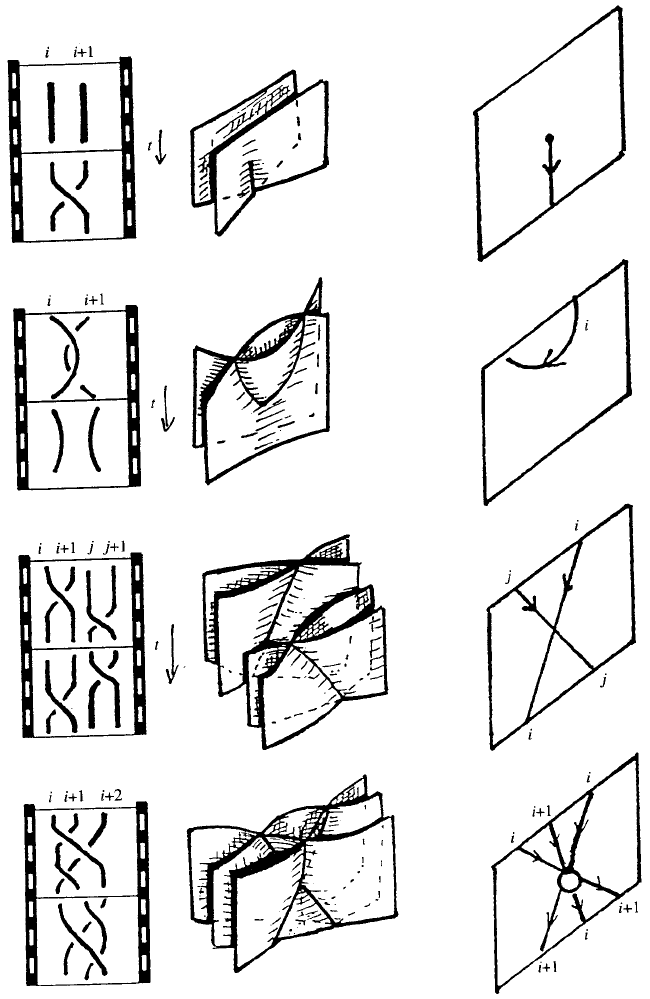
This situation is illustrated in Fig. 5.

Two braid movies are equivalent if they represent e quivalent surface

braids.

2.3 Chart descriptions

A chart is an oriented labelled graph embedded in a dis k, the edges are

labelled with g e nerators of the braid group, and the vertices are of one of

three type s:

(1) A black vertex has valence 1.

(2) A 4-valent vertex can also be thought of as a crossing point of the

edges of the gr aph. The labels on the edges at such a crossing must

be braid generators σ

and σ

where |i − j| > 1.

(3) A white vertex on the chart has valence 6. The edges around the vertex

in cyclic order have labels σ

, σ

where |i −j| = 1. Here,

the orientations are such that the ﬁrst three edges in this labelling

are incoming and the last three edges are outgoing.

Consider the double point set of F under the projection p

: B

×D

⊃

F → B

× D

which is a subset of B

× D

. Then a chart depicts the

image of this double point set under the projection p

: B

× D

→ D

the following sense :

(1) The birth/death of a braid generator occurs at a saddle point of the

surface at which a double-point arc ends at a branch point. This

projects to a black vertex on a chart.

(2) The projection of the braid exchange σ

= σ

for |i − j| > 1 is a

4-valent vertex or a crossing in the graph.

(3) The 6 -valent vertex c orresponds to a Reidemeister type III move, and

this in turn is a triple point of the projected surface.

(4) Maximal and minimal points on the graph cor respond to the birth or

death of σ

−1

, and this is an optimum on the double-point set.

The re lationships among surface projections, braid movies, and charts

is depicted in Fig. 5.

2.3.1 Reconstructing the surface braid from a chart

A chart gives a complete description o f a surface braid in the following way.

Recall that the D

factor of D

is interpreted as a time direction. Thus

200 J. Scott Carter and Masahico Saito

Fig. 5. Braid movies, charts, and diagrams

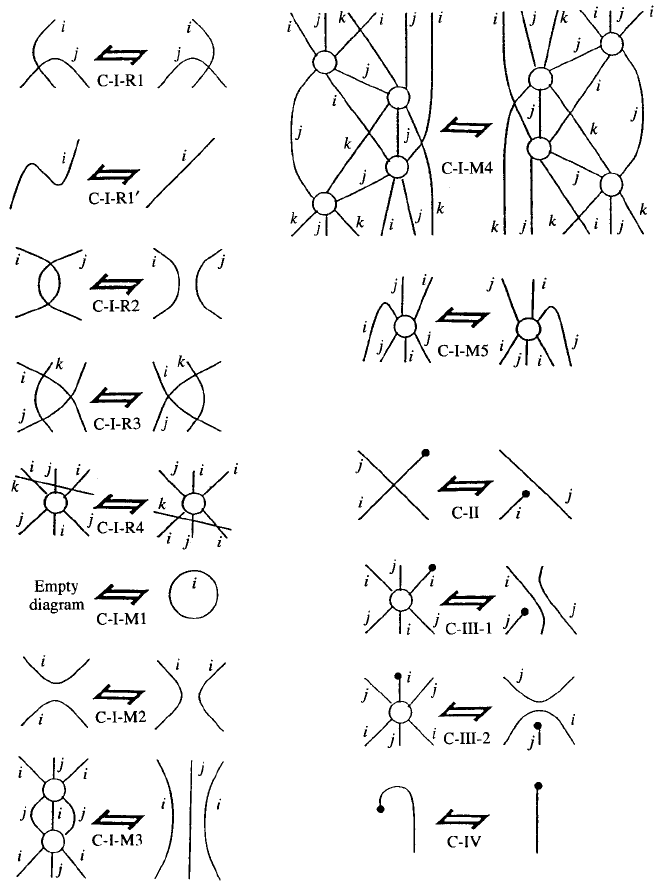
Knotted S urfaces, Braid Movies, and Beyond 201

Fig. 6. Chart moves

202 J. Scott Carter and Masahico Saito

the vertical axis of the disk points in the direction of increasing time. Each

generic intersection of a horizontal line with the graph (generic intersections

will miss the vertices and the critical points on the graph) gives a sequence

of braid words. The letters in the word are the labels associated to the

edges; the exponent on such a generator is positive if the edge is oriented

coherently with the time direction, otherwise the exponent is negative. By

taking a single slice on either side of a vertex or a critical point o n the

graph, we can reconstruct a braid movie from the sequence of braid words

that results. Therefore, given a chart and a braid index, we can construct

a surface braid and, indeed, a knotted surface by closing the surface braid.

Theorem 2.1 (Kamada) Every surface braid gives rise to an oriented

labelled chart, and every oriented labelled chart completely describes a sur-

face braid.

Further more, Kamada provided [25] a set of moves on charts. His list

consists of three moves called CI, II, and III. From the braid movie point of

view, we need to reﬁne his list incorporating movie moves. Such generalized

chart moves, yielding braid movie moves that will be discuss e d in the next

section, are listed in Fig. 6.

2.4 Braid movie moves

The following 14 types of changes among braid movies are called braid

movie moves:

(C-I-R1)

(σ

, σ

−1

, σ

−1

) ↔ (σ

, σ

−1

, σ

−1

where |i − j| > 1.

(C-I-R1

)

(σ

, σ

−1

, σ

) ↔ (σ

(C-I-R2)

(σ

, σ

) ↔ (σ

where |i − j| > 1.

(C-I-R3)

(σ

, σ

) ↔ (σ

, σ

where |i − j| > 1, |j − k| > 1, |k − i| > 1.

(C-I-R4)

(σ

, σ

)

↔ (σ

, σ

where |i − j| = 1 and |i − k| > 1, |j − k| > 1.

Knotted Surfaces, Braid Movies, and Beyond 203

(C-I-M1)

(empty word) ↔ (empty word, σ

−1

, empty word).

(C-I-M2)

(σ

−1

, empty word, σ

−1

) ↔ (σ

−1

(C-I-M3)

(σ

, σ

) ↔ (σ

where |i − j| = 1.

(C-I-M4)

(σ

, σ

)

↔ (σ

, σ

where k = j + 1 = i + 2 or k = j − 1 = i − 2.

(C-I-M5)

(σ

, σ

−1

, σ

−1

) ↔ (σ

, σ

−1

, σ

−1

where |i − j| = 1.

(C-I I)

(σ

, σ

) ↔ (σ

, σ

where |i − j| > 1.

(C-I II- 1)

(σ

, σ

) ↔ (σ

, σ

where |i − j| = 1.

(C-I II- 2)

(σ

−1

, σ

−1

, σ

−1

) ↔ (σ

−1

, empty word, σ

−1

, σ

−1

where |i − j| = 1.

(C-IV)

(empty word, σ

−1

, σ

) ↔ (empty word, σ

Further more, we include the variants obtained from the above by the fol-

lowing rules:

(1) replace σ

with σ

−1

for a ll or so me of i appearing in the s e quences if

possible,

(2) if (b

, . . . , b

) ↔ (b

, . . . , b

) is one of the above, add (b

, . . . , b

) ↔

, . . . , b

204 J. Scott Carter and Masahico Saito

(3) if (b

, . . . , b

) ↔ (b

, . . . , b

) is one of the above, add (c

, . . . , c

) ↔

, . . . , c

) where c

(resp. c

) is the word obtained by reversing the

order of the word b

(resp. b

(4) combinations of the above.

The braid movie moves are depicted in Figs 7 and 8. There is an overlap

between the braid movie moves and the ordinary movie moves; that overlap

is to be expected.

2.5 Deﬁnition (locality equivalence)

Let (b

, . . . , b

) and (b

, . . . , b

) be two braid movies that satisfy the fol-

lowing co ndition. There exists i, 1 ≤ i ≤ n, such tha t

(1) b

= b

for a ll j 6= i − 1, i, i + 1,

(2) b

(resp. b

), j = i − 1, i, i + 1, are written as b

= u

(resp.

= u

) where u and v satisfy

(2a) u

(resp. v

) is obtained from u

i−1

(resp. v

i−1

) by one of

the elementary braid changes, say η, and v

= v

i−1

(resp.

= u

i−1

(2b) v

i+1

(resp. u

i+1

) is obtained from v

(resp. u

) by one of

the elementary braid changes, say ξ, and u

= u

i+1

(resp.

= v

i+1

Then we s ay that (b

, . . . , b

) is obtained from (b

, . . . , b

) by a locality

change (or vice versa). If two braid movies are r e lated by a se quence of lo-

cality changes then they are called equivalent under locality. Loosely speak-

ing, equivalence under locality changes means that distant EBCs commute.

Theorem 2.2 [12] Two braid movies are equivalent if and only if they

are related by a sequence of braid movie moves and locality changes.

It is interesting to note that in the braid movie point of view, the move

that corresponds to a quadruple point g ives a movie move corresponding to

the permutohedral equation rather than to the tetrahedral equation. We

will discuss these equations at some length in Section 3.

3 The permutohedral and tetrahedral equations

In [43], Zamolodchikov presented a system of equations and a solution

to this system that corresponded to the interaction of straig ht strings in

statistical mechanics. This system of equations is related to the Yang–

Baxter equations , and this relationship suggests topological applica tions.

Baxter [1] showed that the Zamolodchikov solution worked. And in

[2] higher-dimensio nal analogues were deﬁned. In [37], these systems are

interpreted as consistency conditions for the obstructions to the lower di-

mensional e quations having solutions. Frenkel and Moore [16] produced

a formulation and a solution of a variant of the Zamolodchikov tetrahe-

dral eq uation. And Kapranov and Voevodsky [27] consider the solution of

Knotted S urfaces, Braid Movies, and Beyond 205

Fig. 7. The braid movie moves

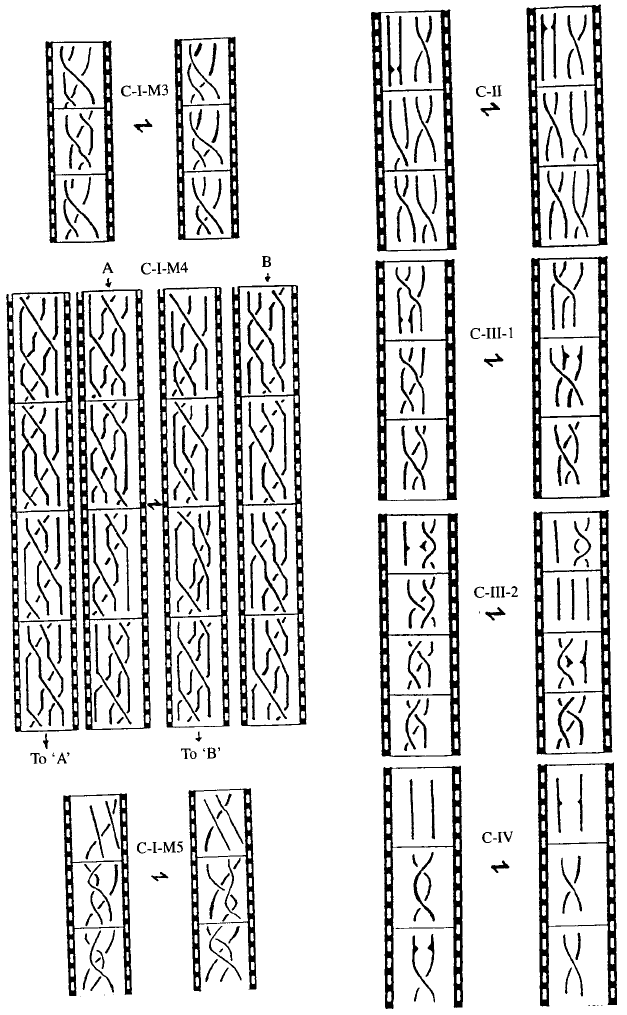
206 J. Scott Carter and Masahico Saito

Fig. 8. The braid movie moves

Knotted Surfaces, Braid Movies, and Beyond 207

the Zamolodchikov equation to be a key feature in the construction of a

braided monoidal 2-category. In a parallel development, Ruth Lawrence

[33] describe d the permutohedral equation and two others as natural e qua-

tions for which solutions in a 3-algebra could be found.

There are other so lutions o f these higher-order equations known to us.

In particular, we mention [13], [19], [28], and [31]. In [32], solutions are

studied in relation to quasicrystals. We expect there are even more solu-

tions in the literature and would appreciate being to ld of these.

Here we review these e quations a nd our methods for solving them.

3.1 The tetrahedral equation

The Frenkel–Moore version of the tetrahedral equation is for mulated as

123

124

134

234

= S

234

134

124

123

(3.1)

where S ∈ End(V

⊗3

), V a module over a ﬁxed ring k. Each side of the

equation acts on V

⊗4

= V

⊗ V

, and S

123

, for example, acts o n

as the identity. Notice here that eqn (3.1) has the nice property that

each index appears three times on either side of the equation.

Compare this equation with the movie move that involves ﬁve frames

on either side. On the left-hand movie, the e lementary string interactions

that occur are Reidemeister type III moves. Label the strings 1 to 4 from

left to right in the ﬁrst frame of the movie. (This index is one more than the

number of string s that cross over the given string.) Then the Reidemeister

type III moves occur in order among the s trings (123), (124), (134), (234).

Thus we think of the tensor S as corresponding to a type III Reidemeister

move. The equation corresponds to the given movie move as these type

III moves occur in opposite order on the right-hand side of the move. This

correspondence was also pointed out by Towber.

3.1.1 A variant

There is a natural variant of this equation:

124

135

236

456

= S

456

236

135

124

(3.2)

where each side of the equation now acts on V

⊗6

. In this equation each

index appears twice in each side. This tetrahedral equation was also for-

mulated in [27, 33, 37].

We review how to obtain eqn (3.2) from eqn (3.1) (cf. [27]). Deﬁne a

set of pa irs of integers among 1 to 4:

C(4, 2) = { 12, 13, 14, 23, 24, 34}

with the lexicographical ordering as indicated. There are six elements and

the ordering deﬁnes a map ξ: C(4, 2) → {1, . . . , 6}. The ﬁrst factor of the

left-hand side of the equation (3.1) is S

123

. Consider the pairs of integers

among this subscript: {12, 13, 23} in the lexicographical ordering. Under

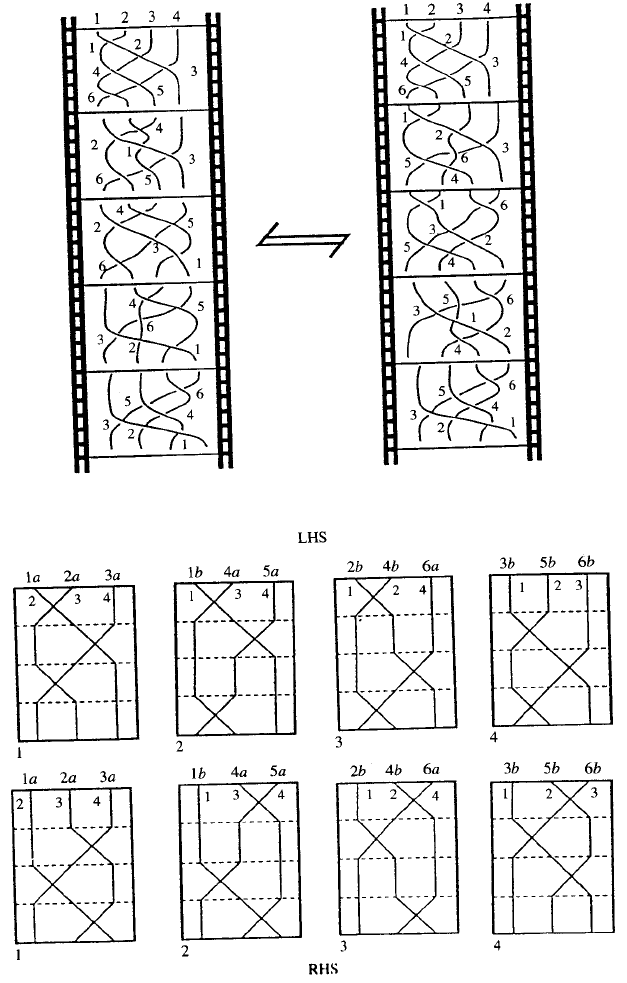
208 J. Scott Carter and Masahico Saito

Fig. 9. Solving the Zamo lodchikov equation