Awange J.,Grafarend E., Palancz B., Zaletnyik P. Algebraic Geodesy and Geoinformatics

Подождите немного. Документ загружается.

96 7 Solutions of O verdetermined Systems







:= 2(X

− X

)dX

− 2(X

− X

)dX + 2(Y

− Y

)dY

−

−2(Y

− Y

)dY − 2S

= 0

:= 2(X

− X

)dX

− 2(X

− X

)dX + 2(Y

− Y

)dY

−

−2(Y

− Y

)dY − 2S

= 0.

(7.39)

Arranging (7.39) with the unknown terms {X

, Y

} = {x

, x

} ∈ x on the left-hand-side

and the known terms

, Y

, X

, Y

, S

} = {y

, y

} ∈ y,

on the right-hand-side leads to





= J













, (7.40)

with







∂f

∂X

∂f

∂Y

∂f

∂X

∂f

∂Y









−2(X

− X

) −2(Y

− Y

)

−2(X

− X

) −2(Y

− Y

)



, (7.41)

and













∂f

∂S

∂f

∂X

∂f

∂Y

0 0 0

0 0

∂f

∂S

∂f

∂X

∂f

∂Y









−2(X

− X

) −2(Y

− Y

) 0 0 0

0 0 0 2S

−2(X

− X

) −2(Y

− Y

)



(7.42)

If we consider that

D{x} = Σ





D{y} = Σ













(7.43)

we obtain with (7.40), (7.41) and (7.42) the dispersion (7.31) of the unknown variables

, Y

} = {x

, x

} ∈ x.

7-3 Gauss-Jacobi combinatorial algorithm 97

7-334 The Gauss-Jacobi combinatorial algorithm

The Gauss-Jacobi combinatorial program operates in three phases. In the ﬁrst

phase, one forms minimal combinations of the nonlinear equations using (7.28) on

p. 93. Using either Gro ebner basis or polynomial resultants, the desired combina-

torial solutions are obtained. The combinatorial results form pseudo-observations,

which are within the solution space of the desired values. This ﬁrst phase in essence

projects a nonlinear case into a linear case.

Once the ﬁrst phase is successfully carried out with the solutions of the vari-

ous subsets forming pseudo-observations, the nonlinear variance-covariance/error

propagation is carried out in the second phase to obtain the weight matrix. This

requires that the stochasticity of the initial observational sample be known in-order

to propagate them to the pseudo-observations.

The ﬁnal phase entails the adjustment step, which is performed to obtain the

barycentric values. Since the pseudo-observations are linearly independent, the

special linear Gauss-Markov model (see Deﬁnition 7.1 on p. 87) is employed.

Stepwise, the Gauss-Jacobi combinatorial algorithm proceeds as follows:

• Step 1: Given an overdetermined system with n observations in m unknowns,

using (7.28), form minimal combinations from the n observations that comprise

m equations in m unknowns.

• Step 2: Solve each set of m equations from step 1 ab ove for the m unknowns

using either Groebner basis or polynomial resultant algebraic techniques.

• Step 3: Perform the nonlinear error/variance-covariance propagation to obtain

the variance-covariance matrix of the combinatorial solutions obtained in Step

• Step 4: Using the pseudo-observations of step 2, and the variance-covariance

matrix from step 3, adjust the pseudo-observations via the special linear Gauss-

Markov model to obtain the adjusted position of the unknown station.

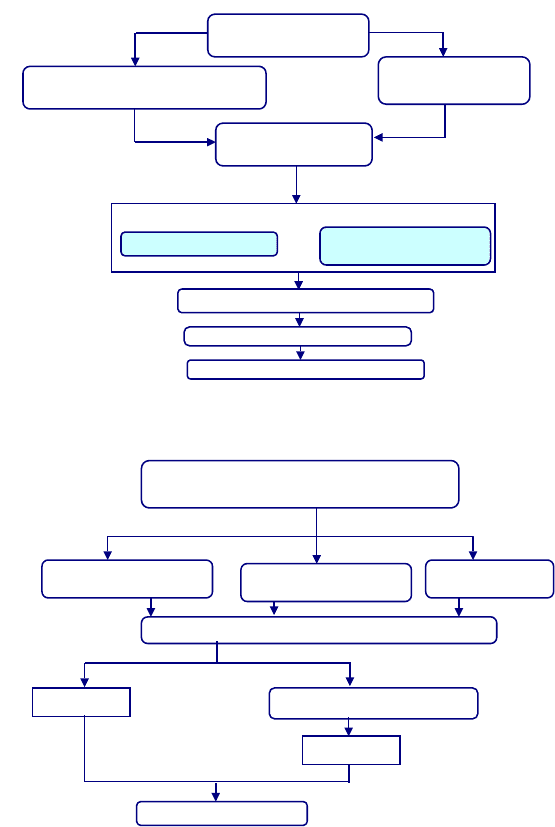
Figure 7.4 summarizes the operations of the Gauss-Jacobi combinatorial algorithm

which employs Groebner basis or p olynomial resultants as computing engines to

solve nonlinear systems of equations (e.g., Fig.7.5).

98 7 Solutions of O verdetermined Systems

Combinatorial

appoach

C.F.GaussPosthumous~(1828)

C.G.I.Jacobi(1841)

Overdetermined

problems

Gröbnerbasis

Resultantapproach

Computationalengine

Nonlinearerrorpropagation

LinearGaussMarkov

Solution

Figure 7.4. Gauss-Jacobi combinatorial algorithm

Matlab/Mathematica/Maple

Nonlinearsystemofmultivariatepolynomials

GröbnerBasis

Solution

Multipolynomial

Resultant

Univariatepolynomial

Backsubstitution

Solution

Linear

Homotopy

Figure 7.5. Combinatorial computing engine

7-4 Concluding remarks

In C haps. 4 and 5, Groebner basis and polynomial resultants algorithms were

presented for solving in exact form the nonlinear sys tems of equations. It was

demonstrated in this chapter how they play a leading role in overcoming the ma-

jor diﬃculty that was faced by C. F. Gauss and C. G. I. Jacobi. The key to success

is to use these algebraic techniques as the computing engine of the Gauss-Jacobi

7-4 Concluding remarks 99

combinatorial algorithm. In s o doing, an alternative procedure to linearized and

iterative numerical procedures that peg their operations on approximate starting

values was presented. Such algebraic technique for solving overdetermined prob-

lems requires neither approximate starting values nor linearization (except for the

generation of the weight matrix). With modern computing technology, the com-

binatorial formation and computational time for geodetic or geoinformatics’ alge-

braic computational problems is immaterial. In the chapters ahead, the power of

this technique will be demonstrated. Further materials on the topic are presented

in [199, 201].

ALESS method has provided a diﬀerent approach for solving overdetermined

systems by transforming them into square systems. Using this method, the num-

ber of equations equals the number of the unknown variables, independently from

the number of equation of the original system. Consequently, overdetermined sys-

tem can be solved eﬃciently with this method (unlike Gauss-Jacobi combinatorial

algorithm where the combinatorial explosion impedes the solution of big overde-

termined systems). The s olution of the transformed square system is pos sible also

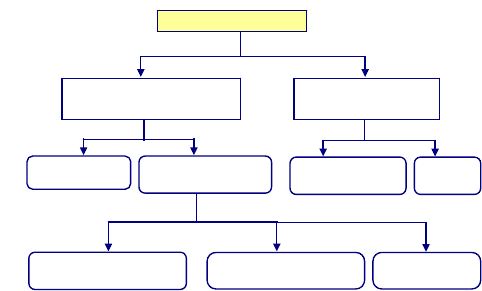
with local and with global methods. Fig. 7.6 gives a summary of the algebraic

algorithms and show when each procedure can be applied.

NonlinearProblems

Nonlinearsystemof

polynomialequations

Overdetermined

problems

Gröbnerbases

Multipolynomial

resultant

Gauss‐Jacobi

combinatorial

F.Macaulay(1902)

formulation

B.Sturmfels(1998)

formulation

ALESS

Dixon‘s

formulation

Figure 7.6. Algebraic solution approach. Here, the nonlinear system of equations implies

determined nonlinear system of equations.

8 Extended Newton-Raphson method

8-1 Introductory remarks

In Chap. 7, we have seen that overdetermined nonlinear systems are common in

geodetic and geoinformatic applications, that is there are frequently more mea-

surements than it is necessary to determine unknown variables, consequently the

number of the variables n is less then the number of the equations m. Mathemati-

cally, a solution for such systems can exist in a least square sense. There are many

techniques to handle such problems, e.g.,:

• Direct minimization of the residual of the system, namely the minimization

of the sum of the least square of the errors of the equations as the objective.

This can be done by using local methods, like gradient type methods, or by

employing global methods, like genetic algorithms.

• Gauss-Jacobi combinatorial solution. Having more independent equations, m,

than variables, n, so m > n, the solution - in a least-squares sense - can be

achieved by solving the





combinatorial square subsets (n×n) of a set of m equations, and then weighting

these solutions properly. The square s ystems can be solved again via local meth-

ods, like Newton-type methods or by applying computer algebra (resultants,

Groebner basis) or global numerical methods, like linear homotopy presented

in Chap. 6.

• Considering the necessary con dition of the minimum of the least square error,

the overdetermined system can be transformed into a square one via computer

algebra (see ALESS in Sect. 7-2). Then, the square system can be solved again

by local or global methods. It goes without saying that this technique works for

non-polynomial cases as well.

• For the special type of overdetermined systems arising mostly from datum

transformation problems, the so called Procrustes algorithm can be used. There

exist diﬀerent types of them, partial, general and extended Procrustes algo-

rithms. These methods are global and practically they need only a few or no

iterations.

In this chapter, a special numerical method is introduced, which can solve

overdetermined or underdetermined nonlinear systems directly. In addition, it

is robust enough to also handle determined systems when the Jacobian is ill-

conditioned. Our problem is to solve a set of nonlinear equations

f(x) = 0 (8.1)

where f:R

→ R

, namely x ∈ R

and f ∈ R

If n = m and the Jacobi matrix has a full rank everywhere, in other words the

system of equations is regular, and if in addition, the initial value of the iteration

J.L. Awange et al., Algebraic Geodesy and Geoinformatics, 2nd ed.,

DOI 10.1007/978-3-642-12124-1 8,

 Springer-Verlag Berlin Heidelberg 2010

102 8 Extended Newton-Raphson method

is close enough to the solution, the Newton-Raphson method ensures quadratic

convergence. If one of these conditions fails, for example the system is over or under

determined, or if the Jacobi matrix is singular, one can use the Extended Newton-

Raphson method, see e.g. [68, 69, 137, 214, 336]. In addition isolated multiple roots

may cause low convergency. To restore quadratic conve rgence, a deﬂation method

can be used, see Zhao [435]. Let us illustrate these problems with the following

examples.

8-2 The standard Newton-Raphson approach

Consider the set of nonlinear equations,

, x

, . . . , x

) = 0, i = 1, . . . , n

which can be written in compact form as

f(x) = 0

We wish to ﬁnd the set of x

satisfying this system, therefore let us to expand it in

a Taylor series about the x

iterate, where the superscript k denotes the iterative

number



k+1



= f





j=1

∂f

∂x





k+1

− x



+ . . .

which deﬁne the Jacobian matrix,

i,j

∂f

∂x



and the set f



k+1



= 0. Then,



k+1

− x



+ f





= 0

or the x

k+1

iteration can be expressed as

k+1

= x

−





−1





Quadratic convergence means that the number of the correct signiﬁcant digits is

doubled at each iteration.

8-3 Examples of limitations of the standard approach

8-31 Overdetermined polynomial systems

Let us consider a simple monomial system (see Sommese and Wampler [367]

8-3 Examples of limitations of the standard approach 103

= x

= 0

= xy = 0

= y

= 0

(8.2)

This system is a “monomial ideal” and trivial for computer algebra. Its Groebner

basis is

G =



, xy, x



(8.3)

whose solutions are,

S = {{y = 0, y = 0}, {x = 0, y = 0}, {x = 0, x = 0}}. (8.4)

We can see that the origin is an isolated s ingular root with multiplicity of 3.

Global polynomial solvers using numerical Groebner basis can also solve this sys-

tem. However, the standard Newton-Raphson method fails, since the system is

overdetermined, although we can transform the overdetermined s ystem into a de-

termined one in a least squares sense. The objective function is the sum of the

square of the residium of the equations,

W = x

+ x

+ y

. (8.5)

Considering the necessary conditions for the minimum, we obtain the following

system,

= 4x

+ 2xy

= 0

= 2x

y + 4y

= 0

(8.6)

Then, using the Newton-Raphson metho d, with initial values ( x

= 1, y

= 1), the

result is,

x = 1.78642 × 10

−8

, y = 1.78642 × 10

−8

The convergence is slow and the accuracy of the solution is poor (even if the initial

guess are changed) because of the existence of multiple roots, see e.g. Chapra and

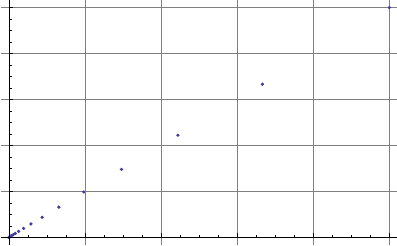
Canale [106]. Fig. 8.1 s hows the steps of the iterations.

0.2

0.4

0.6

0.8

1.0

0.2

0.4

0.6

0.8

1.0

Figure 8.1. Slow convergence for the case of multiple roots (i.e., a plot of x versus y

solutions starting with x = 1, y = 1).

104 8 Extended Newton-Raphson method

The norm of the e rror of the pro ce dure after 45 iteration steps is 2.52639 × 10

−8

Even global minimization with genetic algorithm will give a bad approximation,

x = 1.82247 × 10

−8

, y = 5.29274 × 10

−9

The reason for the s low convergence, as well as for the poor accuracy, is the

increasing multiplicity of the roots (x = 0, y = 0) from 3 up to 9, after transforming

the overdetermined system (f

, f

) into a s quare one (g

, g

8-32 Overdetermined non-polynomial system

A usual test problem for parameter estimation procedures is the Bard [56] problem.

The prototype equation of the system of these nonlinear equations is,

+ d

− a

= 0 (8.7)

where the numerical values of the coeﬃcients are presented in Table 8.1.

Table 8.1 (Coeﬃcients of the Bard equations):

i a

1 0.14 1 15 1

2 0.18 2 14 2

3 0.22 3 13 3

4 0.25 4 12 4

5 0.29 5 11 5

6 0.32 6 10 6

7 0.35 7 9 7

8 0.39 8 8 8

9 0.37 9 7 7

10 0.5 10 6 6

11 0.73 11 5 5

12 0.96 12 4 4

13 1.34 13 3 3

14 2.1 14 2 2

15 4.39 15 1 1

We have 15 equations and 3 unknown parameters, (p

, p

). The system is

overdetermined and not a polynomial one. In this case, the global polynomial

solver, as well as the Newton-Raphson method, fail. The minimization of the sum

of square of errors of the equations,

W (p

, p

) =

i=1

(8.8)

can be done directly via global minimization using, e.g., genetic algorithm leading

to,

8-3 Examples of limitations of the standard approach 105

= 0.0679969, p

= 0.889355, p

= 2.57247.

Alternatively, the overdetermined problem can be transformed into a determined

one, like in the case of polynomials (see ALESS). The necessary conditions of the

minimum.

, p

) =

∂W

∂p

= 0, j = 1, 2, 3 (8.9)

To solve this system (g

, g

), the Newton-Raphson method can be successful,

with initial values (p

, p

) = (1, 1, 1) leading to,

= 0.0679969, p

= 0.889355, p

= 2.57247

However, the method may fail, when the starting values are far from the solution

and the Jacobian becomes singular, which is the case when (p

, p

) = (-1, 1,

1). A global polynomial solver provides a solution, but besides the correct solution,

other real solutions also arise (see Table 8.2 ).

Table 8.2 Solution of the square system (g

, g

0.170869 + 0.0606932i −5.99409 + 7.168i 9.59168 −7.07904i

0.170869 −0.0606932i −5.99409 − 7.168i 9.59168 + 7.07904i

0.22783 −4.44817 8.44473

0.147587 + 0.0939871i −3.42647 + 2.4683i 6.98725 − 2.33614i

0.147587 −0.0939871i −3.42647 − 2.4683i 6.98725 + 2.33614i

0.216599 −2.61935 6.70349

0.114883 + 0.112266i −1.99681 + 1.21785i 5.51067 − 1.06593i

0.114883 −0.112266i −1.99681 − 1.21785i 5.51067 + 1.06593i

0.181359 −1.55169 5.58774

0.077954 + 0.114988i −1.15986 + 0.720556i 4.62469 − 0.570547i

0.077954 −0.114988i −1.15986 − 0.720556i 4.62469 + 0.570547i

0.120499 −0.852832 4.69769

0.0413009 + 0.102133i −0.621754 + 0.449866i 4.04119 −0.321571i

0.0413009 −0.102133i −0.621754 − 0.449866i 4.04119 + 0.321571i

0.0450109 −0.386462 3.96801

0.0119518 + 0.0689036i −0.227926 + 0.275464i 3.61455 − 0.192522i

0.0119518 −0.0689036i −0.227926 − 0.275464i 3.61455 + 0.192522i

0.0679969 0.889355 2.57247

However, only one positive real solution appears, see last row in Table 8.2. This

is because the determined system has more solutions than the original overdeter-

mined system. In addition, the computation time will also increase.

8-33 Determined polynomial system

Now let us consider a determined system of polynomial equations, which is a

somewhat modiﬁed version of the example of Ojika [314],

(x, y) = x

+ y − 3

(x, y) = x +

− 1

(8.10)

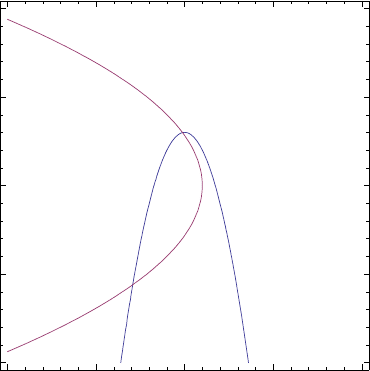
106 8 Extended Newton-Raphson method

First, let us try to solve the problem using the Newton-Raphson method, starting

with (x

= -1, y

=-1). The result is

x = 1.56598, y = 1.27716

which is not correct (compare with Fig. 8.3). The norm of error is 1.06057. The

situation is the same with (x

= 1, y

= -1) which gives

x = 1.27083, y = 1.57379.

Again, this is not a s olution. The norm of error is 0.061036, so the Newton-Raphson

method fails.

x,y

1



1



Figure 8.2. Real roots of the system of the two polynomials of Eqn. 8.10

8-34 Underdetermined polynomial system

Let us consider the following underdetermined system, see Quoc-Nam Tran [337]

= (x − u)

+ (y − v)

− 1

= 2v(x − u) + 3u

(y − v)



3wu

− 1



(2wv − 1)

(8.11)

It goes without saying that the system has inﬁnite roots. To make the solution

unique, one may consider the solution with the minimal norm. This constraint

leads to the following minimization problem,