Awange J.,Grafarend E., Palancz B., Zaletnyik P. Algebraic Geodesy and Geoinformatics

Подождите немного. Документ загружается.

8-4 Extending the Newton-Raphson approach using pseudoinve rse 107

W (x, y, u, v, w) =

+ y

+ u

+ v

+ w

→ min W

x,y , u,v,w

(8.12)

under the constrains,

= 0, i = 1, 2, 3 (8.13)

It is clear that the Newton-Raphson method can not be used. Employing genetic

algorithm, we get,

x = 0.187018, y = −1.08919 × 10

−6

, u = 0.81298, v = 0.000124852, w = 0.504332

with a norm of 0.975.

8-4 Extending the Newton-Raphson approach using

pseudoinverse

Now, in order to avoid these diﬃculties an extension of the Newton - Raphson

method can be introduced, see [337]. This method uses the pseudoinverse of the

Jacobian, instead of its inverse. The computation of the pseudoinverse is based on

the singular value decomposition technique. Every A matrix m ×n, m ≥ n can be

decomposed as

A=UΣV

(8.14)

where (.)

denotes the transposed matrix, U an m × n matrix, and V an n × n

matrix satisfying

U=V

V = VV

= I

(8.15)

and Σ =< σ

, ..., σ

> a diagonal matrix. These σ

’s, σ

≥ σ

≥, ..., σ

≥ 0 are

the square root of the non negative eigenvalues A

A and are called the singular

values of matrix A. As it is known from linear algebra e.g. Bernstein [73], singular

value decomposition (SVD) is a technique used to compute the pseudoinverse for

a singular or ill-conditioned matrix of linear systems. In addition, this method

provides a least square solution for overdetermined systems and minimal norm

solutions for the case of undetermined systems.

The pseudoinverse of a matrix A of m ×n is a matrix A

of n ×m satisfying

A = A, A

= A





∗

= A





∗

= AA

(8.16)

where (.)

∗

denotes the conjugate transpose of the matrix. There always exists a

unique A

which can be computed using SVD: (a) If m ≥ n and A = UΣV

then

= VΣ

−1

(8.17)

where Σ

−1

=< 1 /σ

, ..., 1 /σ

> . b) If m < n then compute the



)

, pseu-

doinverse of A

and then





)



(8.18)

108 8 Extended Newton-Raphson method

The idea of using pseudoinverse in order to generalize the Newton-Raphson method

is not new. It means that in the iteration formula (8.19), the pseudoinverse of the

Jacobian matrix will be em ployed instead,

i+1

= x

− J

) f (x

) (8.19)

The pseudoinverse can be computed in a symbolic as well as a numeric form.

For e xample, considering the ﬁrst example, see Sommese and Wampler’s [367]

equations in Sect. 16-21, the Jacobi matrix is

J(x, y) =





2x 0

y x

0 2y





(8.20)

and its pseudoinverse

(x, y) =

+4xy

2(x

+4x

)

+4x

−

2(x

+4x

)

−

2(x

+4x

)

+4x

y +y

2(x

+4x

)

(8.21)

The Jacobian matrix at the point (x

= 1 , y

= 1) is,

J(1, 1) =





2 0

1 1

0 2





(8.22)

and the pseudoinverse is

(1, 1) =



−



(8.23)

The new values ( x

i+1

, y

i+1

) in the next iteration step are





− J

(1, 1)





(1, 1)









(8.24)

8-5 Applications of the Extended Newton-Raphson method

Example 8.1 (Overdetermined polynomial system). Let us recall the Sommese

and Wampler’s [367] equations solved in Sect. 8-31. Using the Extended Ne wton-

Raphson method with initial values (x

= 1, y

= 1), we get the solution (after 40

iterations) as

x = 1.8189894035458573 × 10

−12

, y = 1.81899 × 10

−12

The convergence is shown in Fig. 8.3 and the norm of error is 2.5724394843074972×

−12

. We therefore achieved a considerably more accurate result with approxi-

mately the same number of iteration steps as that of Sect. 8-31. This means faster

convergency.

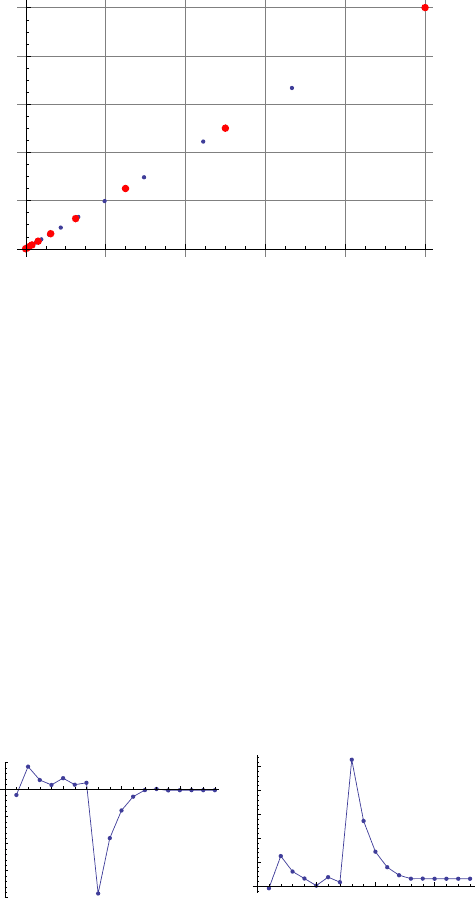
8-5 Applications of the Extended Newton-Raphson method 109

0.2

0.4

0.6

0.8

1.0

0.2

0.4

0.6

0.8

1.0

Figure 8.3. Convergence of the Extended Newton-Raphson method (big points) while

that of the standard Newton-Raphson (small points)

Example 8.2 (Overdetermined non-polynomial system). Extended Newton-Raphson

method can solve directly the original overdetermined system of Sect. 8-32 with

both initial conditions more quicker than the standard methods (see Chap. 7)

when solving the transformed square one system of equations. In addition, no

transformation of the overdetermined model into a square one is necessary.

Example 8.3 (Determined system with singular Jacobian). The Extended Newton

Raphson method converge s from all of the diﬀerent initial values for the c ase

of the Ojika [314] problem that we attempted to solve in Sect. 8-33 using the

standard Newton-Raphson method (i.e., obtaining the roots of the system of the

two polynomials of Eqn. 8.10). Figs.8.4- 8.6 illustrate the fast convergence obtained

when Extended Newton-Raphson is obtained as opposed to the standard Newton-

Raphson (see Fig. ).

2

1



Figure 8.4. Convergence when starting values are (-1, -1)

Example 8.4 (Underdetermined system). The result produced by the Extended

Newton-Raphson method depends on the initial condition, which is natural in

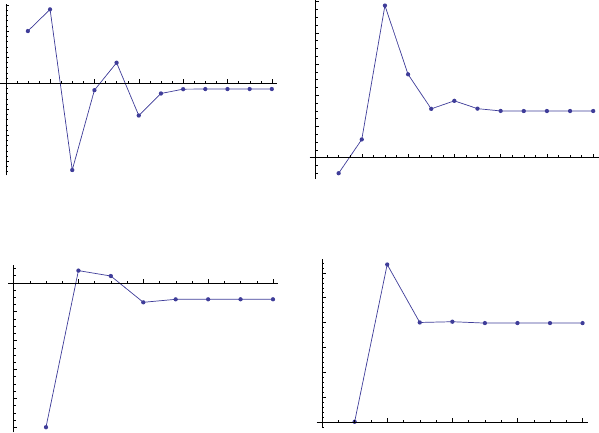
110 8 Extended Newton-Raphson method

1

0

0.5

1.0

1.5

Figure 8.5. Convergency when starting values are (1, -1)

1

0

1.5

2.0

2.5

3.0

3.5

4.0

Figure 8.6. Convergency when starting values are (-1, 1)

the case of a local me thod, but no divergence takes place. In order to get the so-

lution with the minimal norm, we computed the solutions with 500 initial values

generated randomly in the interval [- 0.5, 0.5]. The computation took 1.422 sec

and the norm of the solution was 0.977. While using global constrained minimiza-

tion via ge netic algorithm, the computation needed 2.390 sec and the norm of the

solution was 0.975.

8-6 Concluding remarks

The examples demonstrate the eﬃciency and eﬀectiveness of the suggested method,

especially for cases of overdetermined systems. Although the Extended Newton-

Raphson procedure is a local method, the solution of a square subset of the overde-

termined system can provide a good initial guess for the computation. As a side

eﬀect, the method can also solve determined ill- conditioned problems frequently

arising from geometrically ill-posed conﬁgurations e.g. in GPS positioning [41] or

in solving datum transformation problems, see [430]. In addition, the implementa-

tion of this method is quite easy, since the computation of inverse of the Jacobian

matrix could be simply replaced by the pseudoinverse in any Newton - Raphson

procedure.

9 Procrustes solution

“It seems very strange that up to now Procrustes analysis has not been

widely applied in geodetic literature. With this technique linearization prob-

lems of non linear equations system and iterative procedures of computation

could be avoided, in general, with signiﬁcant time saving and less analytical

diﬃculties” F. Crosilla.

9-1 Motivation

This chapter presents the minimization approach known as “Procrustes” which

falls within the multidimensional scaling techniques discussed in Sect. 9-22. Pro-

crustes analysis is the technique of matching one conﬁguration into another in-

order to produce a measure of match. In adjustment terms, the partial Procrustes

problem is formulated as the least squares problem of transforming a given matrix

A into another matrix B by an orthogonal transformation matrix T such that

the sum of squares of the residual matrix E = A − BT is minimum. This tech-

nique has been widely applied in shape and factor analysis. It has also been used

for multidimensional rotation and also in scaling of diﬀerent matrix conﬁgura-

tions. In geodesy and geoinformatics, data analysis often require scaling, rotation

and translation operations of diﬀerent matrix conﬁgurations. Photogrammetrists,

for example, have to determine the orientation of the camera during aerial pho-

togrammetry and transform photo coordinates into ground coordinates. This is

achieved by employing scaling, translation and rotation operations. These ope ra-

tions are also applicable to remote sensing and Geographical Information System

(GIS) where map coordinates have to be transformed to those of the digitizing

table. In case of robotics , the orientation of the robotic arm has to b e determined,

while for machine and computer visions, the orientation of the Charge-Coupled

Device (CCD) cameras has to be established. In practice, positioning with satel-

lites, particularly the Global Navigation Satellite Systems (GNSS) such us GPS

and GLONASS has been on rise. The anticipated GALILEO satellites will further

increase the use of satellites in positioning. This has necessitated the transfor-

mation of c oordinates from the Global Positioning System (WGS 84) into local

geodetic systems and vice versa.

A classical problem in geodesy and geoinformatics that would beneﬁt from this

technique is transformation, and in particular the 7–parameter datum transfor-

mation problem. The traditional approach of solving this problem, for instance,

has been to linearize the nonlinear equations and then apply least squares method

iteratively. With the proposed Procrustes approach, all that is required of the user

is to insert the coordinates of one system (e.g., local coordinate system) in say, the

matrix A, and those of the other system (e.g., GPS in WGS-84) into the matrix B.

Using Procrustes analysis technique presented in this chapter, and later in Chap.

17, the desired scale, rotation and translation parameters can be obtained directly.

J.L. Awange et al., Algebraic Geodesy and Geoinformatics, 2nd ed.,

DOI 10.1007/978-3-642-12124-1 9,

 Springer-Verlag Berlin Heidelberg 2010

112 9 Procrustes solution

Although long applied in other ﬁelds such as; sociology, to map crime versus

cities, and also in medicine as we will see in Sect. 9-23, Procrustes method is rela-

tively new to the ﬁelds of geodesy and geoinformatics. Its ﬁrst entry into geodesy

can be traced back to the work of [120, 121] where the method was used in the

creation of the criterion matrix used for deformation analysis. Further applications

include the works of [16, 168, 169] who applies it to compute the three-dimension

orientation parameters, deﬂection of the vertical, and 7-parameter datum trans-

formation.

Recent application of the approach in geoinformatics can be found in the works

of [123] who employs it to solve the photogrammetric block adjustment by inde-

pendent models, [65] who applies it for size and shape three-dimensional object

reconstructions, and [66] who uses the technique to update cadastral maps. At the

beginning of the Chapter, we quoted F. Crosilla [122], the father of Procrustes in

geodesy and geoinformatics. He wonders why such an amazing technique has not

been widely applied in geodesy.

Procrustes method is a very eﬀective method for determining the Helmert’s

datum transformation parameters since it requires neither initial starting values

nor iteration. Due to this attractive attribute, the ABC-Procrustes algorithm ex-

tended it to solve the 3D aﬃne transformation problem where scale factors are

diﬀerent in the 3 principal directions X, Y, Z. In this study, it is illustrated that

such direct extension is restricted to cases of mild anisotropy in scaling. For strong

anisotropy, however, the procedure fails. The PZ-method is proposed as an exten-

sion of the ABC algorithm in case of strong anisotropy. The procedures are applied

to determine transformation parameters for; (i) transforming Australian Geodetic

Datum (AGD 84) to Geocentric Datum Australia (GDA 94), i.e., mild anisotropy

and (ii) the Hungarian datum (strong anisotropy). The results indicate that the

PZ-algorithm leads to a global minimization as opposed to the ABC-algorithm al-

beit with slightly longer computational time. However, the ABC-method is found

to be useful for computing proper initial values for PZ-method thereby increasing

its eﬃciency.

In this chapter, the partial, also called simple Procrustes algorithm which is

suﬃcient for solving only the rotation elements is presented. It will be demon-

strated how the approach solves the three-dimensional orientation and the vertical

deﬂection (direction of local gravity vector) problems. In Chap. 17, the general

Procrustes algorithm will be presented and used to solve the 7-parameter similar-

ity transformation problem which is often encountered in practice.

9-2 Procrustes: Origin and applications

9-21 Procrustes and the magic bed

The origin of the name, and perhaps the concept is traced back to Greece. Some-

where in Attica in Greece lived a robber whose name was Procrustes. His house

was so well positioned besides the road such that he was frequented by visitors

9-2 Procrustes: Origin and applications 113

who had to spend the night. In his house, Procrustes also known as Damastes kept

a special bed: So special was the bed such that the visitors were required to ﬁt

in it. Unfortunately for Procrustes, neither were all his visitors of the same height

nor length of the magic bed. All the same, the visitors were somehow forced in

some “magic” way to ﬁt into the magic bed. This was not done by adjusting the

bed, but to the contrary its occupants! Procrustes devised ways to ﬁt his quests

onto his bed. Guests who were shorter for the bed were stretched by hammering

or racking their bodies to ﬁt the bed, while those who were longer had their legs

chopped oﬀ! In both cases, the victims died. As fate would have it, Procrustes was

himself adjusted to ﬁt his own bed by Theseus, a young Attic hero whose mission

was to eliminate robbers. The Encyclopedia of Greek Mythology writes

“Procrustes (proh-KRUS-teez). A host who adjusted his guests to their

bed. Procrustes, whose name means “he who stretches”, was arguably the

most interes ting of Theseus’s challenges on the way to becoming a hero.

He kept a house by the side of the road where he oﬀered hospitality to

passing strangers, who were invited in for a pleasant meal and a night’s

rest in his very special bed (see Fig. 9.1

). Procrustes described it as having

the unique property that its length exactly matched whomsoever lay down

upon it. What Procrustes didn’t volunteer was the method by which this

“one-size-ﬁts-all” was achieved, namely as soon as the guest lay down

Procrustes went to work upon him, stretching him on the rack if he was

too short for the bed and chopping oﬀ his legs if he was too long. Theseus

turned the tables on Procrustes, fatally adjusting him to ﬁt his own b e d.”

Figure 9.1. Procrustes and his “magical” bed

This magic bed of Procrustes has become a saying for arbitrarily - and perhaps

ruthlessly - forcing someone or something to ﬁt into an unnatural scheme or pat-

tern.

http://www.mythweb.com/encyc/gallery/procrustes c.html

Mythweb.com

114 9 Procrustes solution

9-22 Multidimensional scaling

Multidimensional scaling (MDS) is a method that represents meas urements of

similarity (or dissimilarity) among pairs of objects such as distances between points

of low-dimensional multidimensional space. Let us consider for example that data

consists of intelligence tests and that one desires to see the correlation between the

tests. MDS can be used to represent these data in a plane such that the correlation

can be studied. The more closer the points are (i.e., the shorter the distances

between the points), the more correlated they are. MDS thus gives an advantage

of graphical visualization of hidden adherent properties between objects. MDS has

been described by [87] as:

• An approach for representing similarity and dissimilarity data as exempliﬁed

by distances of low dimensional space. This is done in-order to make this data

accessible for visual inspection and exploration.

• An approach for testing if and how certain criteria by which one distinguishes

among diﬀerent objects of interest are mirrored in a corresponding empirical

diﬀerences of this object (i.e., correlated).

• A data analytic approach that allows one to discover the three-dimensions that

underlie judgements of dissimilarity and similarity.

• A psychological model that explains judgements of diss imilarity in terms of a

rule that mimics a particular type of distance function.

Procrustes approach therefore is a procedure that is applied to realize the goals

of MDS. In other words, it is a tool of MDS concerned with the ﬁtting of one

conﬁguration into another as close as possible.

9-23 Applications of Procrustes in medicine

As a m otivational urge to embrace this long overdue powerful tool, this section

presents brieﬂy two areas where Procrustes procedure has found practical appli-

cation. These are:

• Procrustes application software for gene recognition [150].

• Identiﬁcation of malarial parasites [130].

The technique has also been applied in various ﬁelds ranging from biology, psy-

chology, to structural analysis etc.

9-231 Gene recognition

Gene recognition started as a statistical analysis and splicing sites. The statis-

tical procedures however could not deal with other types of genes such as eu-

karyotic (i.e., a single-celled or multicellular organism whose cells contain a dis-

tinct membrane-bound nucleus). To solve this problem, researchers in the ﬁeld

developed PROCRUSTES software, which uses similarity-based approach to gene

9-2 Procrustes: Origin and applications 115

recognition [150]. This was achieved using spliced alignment technique. The soft-

ware is reported by Human Genome News

to be able to identify with remarkable

accuracy human version of genes that are in other forms of life. The human genes

are broken into smaller segments known as exons. Searching for exons is analo-

gous to following a magazine article that appears in, say, pp. 5, 23, 84, and 93,

with almost identical advertisement and other articles appearing between. The

software is applied to construct all these pages that contain the required article

and automatically combine them into a best ﬁtting set. The technique is said to

work best when a “target protein” from the nonhuman sample guides the search,

thus ensuring an accuracy that approaches 100%. In this technique, if a genomic

sequence and a set of candidate exons are given, the algorithm explores all possible

exon as semblies and ﬁnds a chain with the best ﬁt to relate target protein. Instead

of trying to identify the correct exons by statistical means (which predicts the

correlation between the predicted and the actual gene to 70%, with just 40-50%

exons predicted correctly), PROCRUSTES considers all possible chain with the

maximum global similarity to the target protein. The procedure predicts a corre-

lation of about 99% between the predicted and the actual gene [150]. The tool is

useful in pinp ointing elusive human version of cancer-causing gene!

9-232 Identiﬁcation of malaria parasites

Dryden [130] applies Procrustes to identify proteins by comparing the elec-

trophoretic gel images (Fig. 9.2

). The gels are obtained from strains of parasite

which carry malaria. The procedure uses Procrustes matching and aﬃne shape

registration to match the gels. It applies some biological material to the left corner

of the two images of gels A and B in Fig. 9.2. The material is then separated down

the gel according to molecular weight (with the highest on top) and across the

gel according to isoelectric point (with the highest on the right of the gel). Gel

image is then used to identify strains of parasites using pattern of spots marked

by (+). Dark spots appearing on the gels indicate the composition of protein and

are marked by some expert in both gels A and B. Ten spots are marked in each

gel and then classiﬁed as either invariant or variant spots.

The invariant spots are considered to be present for all parasites. The arrange-

ment of the variant spots is of particular interest as it helps in the identiﬁcation

of malarial parasite. The ﬁeld problem sighted by [130] however is that gels are

prone to deformation such as translation, scaling, rotation, aﬃne transformation

and smooth-linear bending. Gel images therefore need to be registered by matching

each image using a set of transformation to alleviate the deformations above [130].

This is achieved through the use of Procrustes analysis.

July-September 1996; 8:(1)

Chapman and Hall Press

116 9 Procrustes solution

Figure 9.2. The electrophoretic gels from gel A and gel B. Ten invariant spots have

been marked by (+) in white above

Chapman and Hall Press

9-3 Partial procrustes solution

9-31 Conventional formulation

Procrustes being a technique of matching one conﬁguration into another and pro-

ducing a measure of match, seeks the isotropic dilatation and the rigid translation,

reﬂection and rotation needed to best match one conﬁguration to another [116, p.

92]. In this chapter, the term partial shall be used to mean optimal rotation

in-order to avoid confusion since the term is used diﬀerently by diﬀerent authors.

For example, [197, 198] considers a case where the conﬁguration matrix has sev-

eral unknown elements in the minimization of the Frobenius norm as the partial

Procrustes problem. Dryden [130] on the other hand uses the term partial Pro-

crustes to refer to minimization of the Frobenius norm only over the translation

and rotation. The general Procrustes solution is used as the minimization over the

full set of similarity transformation as shall be seen in Chap. 17. In the solution of

partial Procrustes problem, we refer to Table 9.1 for some matrix properties which

will be of use.

The Procrustes problem is concerned with ﬁtting a conﬁguration B into A as

close as possible. The simplest Procrustes case is one in which both conﬁgurations

have the same dimensionality and the same number of points, which can be brought

into a 1 − 1 correspondence by substantive considerations [87, p. 339]. Let us

consider the case where both A and B are of the same dimension. The partial

Procrustes problem is then formulated as

A = BT (9.1)

The rotation matrix T in (9.1) is then solved by measuring the distances between

corresponding points in both conﬁgurations, square these values, and add them to