Awange J.,Grafarend E., Palancz B., Zaletnyik P. Algebraic Geodesy and Geoinformatics

Подождите немного. Документ загружается.

6-4 Solving nonlinear equations via homotopy 65

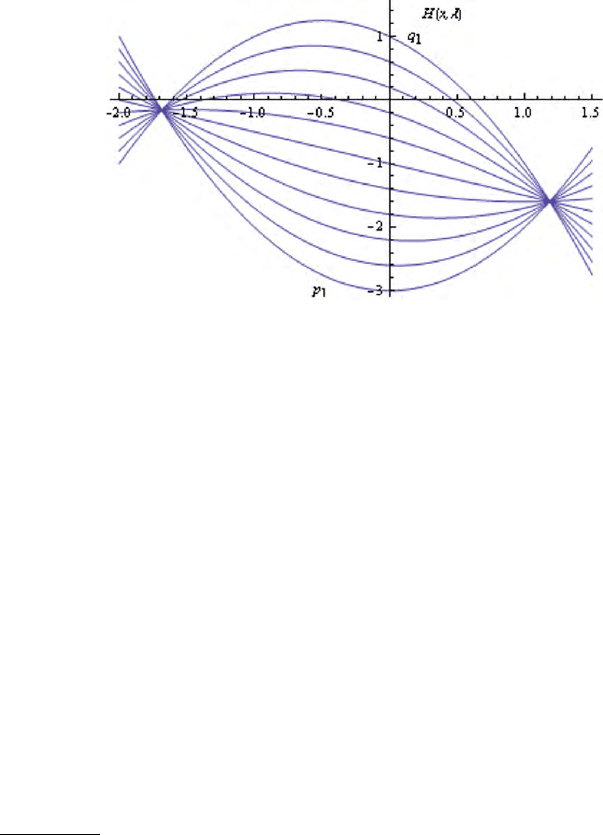
In geometric terms, the homotopy H provides us with a continuous deformation

from p

, which is obtained for λ = 0 by H(x, 0), to q

, which is obtained for λ = 1

by H(x, 1). The homotopy function for diﬀerent λ values, λ = 0, 0.1, . . . , 1 can be

seen on Fig. 6.1. It is called linear homotopy because H is a linear function of the

variable λ.

Figure 6.1. The homotopy H for the polynomials p

and q

(Eqns. 6.1 to 6.3) for diﬀerent values of λ. Note λ = 0 (p

) and λ = 1 (q

The polynomial p

is called the start system and the polynomial q

is called

the target system.

6-4 Solving nonlinear equations via homotopy

The homotopy continuation method deforms continuously the known roots of the

start system into the roots of the target system. Now, let us look at how homotopy

can be used to solve a simple polynomial equation. Considering a polynomial of

degree two (i.e., a quadratic equation),

q(x) = x

+ 8x − 9, (6.4)

whose roots (q(x) = 0) are desired. Instead of this polynomial, we consider a

simpler one by deleting the middle term. The roots of this simpler polynomial can

be found easily by inspection,

p(x) = x

− 9. (6.5)

Remark: In some cases when the starting values are not complex, it is reasonable

to use the “gamma trick” (see [367]), introducing a random complex constant gamma in

the homotopy function: H(x, λ) = (1 −λ)p(x) + λγq(x), because some singular solutions

may lead to problems for Newton’s method.

66 6 Linear homotpy

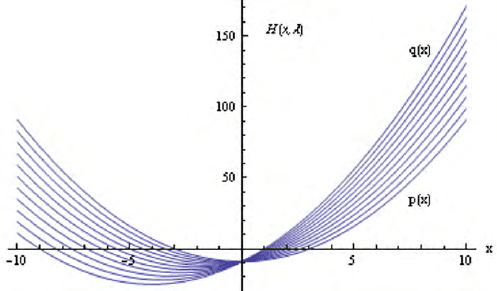
This polynomial also has two roots and will be considered as the start system

for the target system, equation (6.4). The linear homotopy can then be deﬁned as

follows (see Fig. 6.2)

H(x, λ) = (1 − λ)p(x) + λq(x)

= (1 − λ)



− 9



+ λ



+ 8x − 9



= x

+ 8xλ − 9.

(6.6)

Figure 6.2. The homotopy H (Eqn. 6.6) for the polynomials p(x) and q(x)

(Eqns. 6.4 and 6.5, respectively)

The homotopy continuation method deforms continuously the known roots of the

start system p(x) = 0, into the roots of the target system q(x) = 0 (see Fig. 6.3

and Fig. 6.5). Let us solve the equation H(x, λ) = 0 for diﬀerent values of λ as a

parameter. Considering x

= 3, one of the solutions of p(x) = 0, as an initial guess

value, and solving H(x, λ

) = 0, where λ

= 0.2, we employ the Newton-Raphson

method repeatedly, with λ

= 0.2, 0.4, 0.6, 0.8, 1.0 (see Table 6.1 and Fig. 6.3) by

= NewtonRaphson (H (x, λ

) , {x, x

i−1

}) , (6.7)

where x

i−1

is the initial value for the Newton-Raphson method.

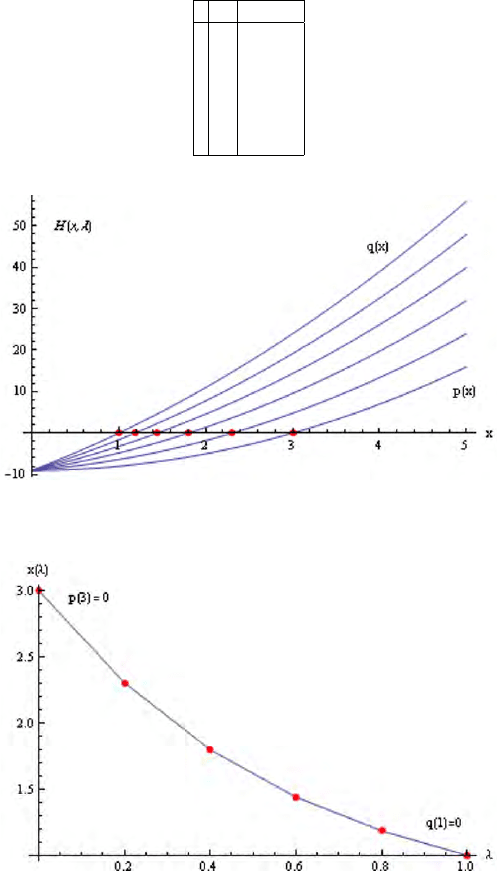
The homotopy path is the function x = x(λ), where in every point H(x, λ) = 0,

see Fig. 6.4. The points in Fig. 6.4. represent the discrete points of the homotopy

path, where H(x

, λ

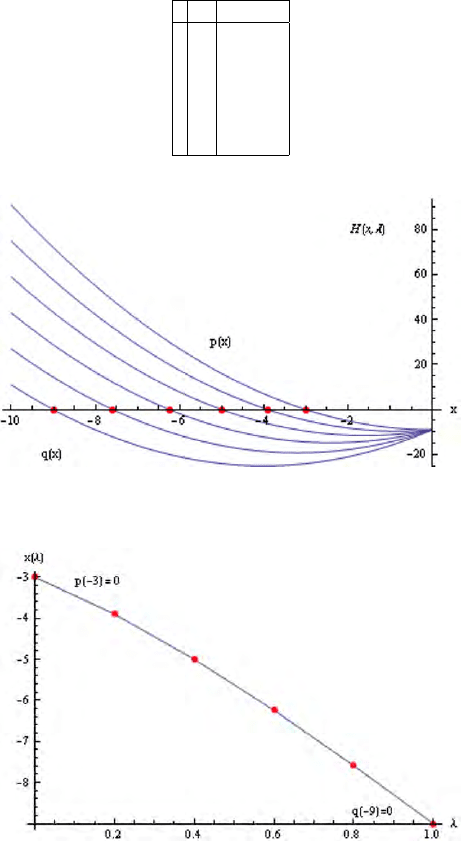
) = 0 for every i = 0, . . . , 5. The second root of Eq(6.4) can be

computed similarly by starting from x

= −3. We now obtain the following values,

shown in Table 6.2 and Fig. 6.5, with the points of the homotopy path shown in

Fig. 6.6.

6-4 Solving nonlinear equations via homotopy 67

Table 6.1. The roots of the deforming polynomials for the case of x

= 3 (Eqn. 6.7)

i λ

0 0.0 3.00000

1 0.2 2.30483

2 0.4 1.80000

3 0.6 1.44187

4 0.8 1.18634

5 1.0 1.00000

Figure 6.3. Deformation of a root of the p olynomial p(x) into a root of the polynomial

q(x) for the case of x

= 3

Figure 6.4. The path of homotopy transforming the root of p(x) into the root of q(x)

for the case of x

= 3

68 6 Linear homotpy

Table 6.2. The roots of the deforming polynomials for the case of x

= −3

i λ

0 0.0 -3.00000

1 0.2 -3.90483

2 0.4 -5.00000

3 0.6 -6.24187

4 0.8 -7.58634

5 1.0 -9.00000

Figure 6.5. Deformation of a root of the p olynomial p(x) into a root of the polynomial

q(x) for the case of x

= −3

Figure 6.6. The path of homotopy transforming the root of p(x) into the root of q(x)

for the case of x

= −3

6-4 Solving nonlinear equations via homotopy 69

6-41 Tracing homotopy path as initial value problem

Comparing the homotopy solution with the traditional Newton-Raphson solution,

if ∆λ is small enough, the convergence may be ensured in every step. One can

consider this root-tracing problem as an initial value problem of an ordinary dif-

ferential equation. Considering H(x, λ) = 0 for every λ ∈ [0, 1], therefore

dH(x, λ) =

∂H

∂x

dx +

∂H

∂λ

dλ ≡ 0 λ ∈ [0, 1]. (6.8)

Then the initial value problem is

dx(λ)

dλ

+ H

= 0 (6.9)

with

x(0) = x

. (6.10)

Here, H

is the Jacobian of H with respect to x

, i = 1, . . . , n, for the case of

n nonlinear equations with n variables. In our single variable case, see Eq(6.6),

∂H

∂x

= 2x + 8λ (6.11)

and

∂H

∂λ

= 8x. (6.12)

Considering that x = x(λ), we obtain

dx(λ)

dλ

= −

8x(λ)

2x(λ) + 8λ

= −

4x(λ)

x(λ) + 4λ

(6.13)

with the initial value

x(0) = 3. (6.14)

The initial value problem given by Eqns. (6.13) and (6.14) can be solved by

any numerical integration technique. The most simple is the Euler method and the

most popular is the Runge-Kutta method and its numerous variations, see [106].

Here we employed the built-in solver of Mathematica, NDSolve, see [208, 320]).

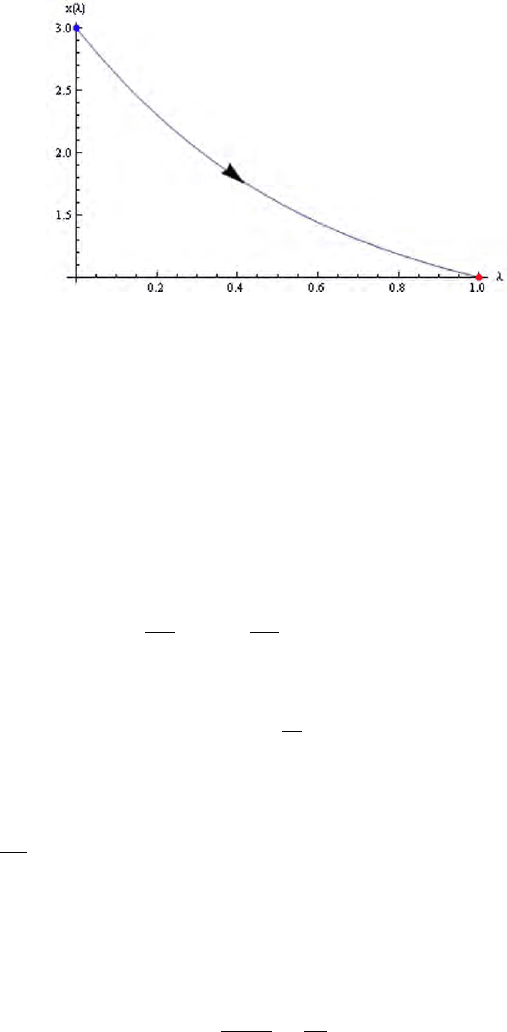
The numerical solution of this initial value problem can be seen in Fig. 6.7. for the

case of x

= 3.

This is the continuous path of the homotopy function, Eq(6.6), where in every

point H(x, λ) ≡ 0. Then one of the roots of the target system, Eq(6.4) is x(1) = 1.

Considering x

= −3 as the initial value, we get the other root, x(1) = −9. In

the multivariate c ase we have to compute the inverse of the Jacobian, namely the

initial value problem which is expressed as

dx(λ)

dλ

= −H

−1

(6.15)

70 6 Linear homotpy

Figure 6.7. Solution of homotopy equation as an the initial value problem

with

x(0) = x

. (6.16)

Here H

−1

is the inverse of the Jacobian H

with respect to x

, i = 1, . . . , n, in

the case of n nonlinear equations with n variables. To carry out the numerical

integration, any numerical method can be used, for example the Runge-Kutta

method. The inverse can be computed in a symbolic way for a limited size like n= 6

or 8. For larger systems, a special method is employed, which is more eﬀ ective than

any other standard numerical computation of the inverse of a matrix, see [147].

We consider a new parameter in equation (6.8), namely the parameter t, then

dH(x(t), λ(t)) =

∂H

∂x

dx(t) +

∂H

∂λ

dλ(t) ≡ 0 λ(t) ∈ [0, 1]. (6.17)

This means that with s(t) = {x(t), λ(t)} we obtain

(s(t))

= 0, (6.18)

where H

is the Jacobian of the homotopy function with respec t to s having n + 1

dimensions. Then the i

derivative function can be expressed as

= (−1)

i+1

det



(1)

, . . . , H

(i−1)

, H

(i+1)

, . . . , H

(n+1)



, (6.19)

where H

(i)

is the i

column of the Jacobian matrix H

(s(t)), see [147]. However,

in that case one needs to check the upper bound of the integration parameter,

since integration should be c arried out up to t

∗

, where λ(t

∗

) = 1, see e.g., [80].

Therefore, it is reasonable to eliminate the last derivative of vector s, namely

n+1

dλ

. (6.20)

Considering that

6-4 Solving nonlinear equations via homotopy 71

dλ

n+1

, (6.21)

and

dλ

n+1

, (6.22)

for i = 1, 2, . . . , n. The integration now can be carried out with the independent

variable λ on [0, 1].

Sometimes the integration can fail because of a singularity in the Jacobi ma-

trix of H(x, λ). In order to avoid this, we consider a modiﬁed complex homotopy

function,

H(x, λ) = γ(1 − λ)p

(x) + λq

(x) (6.23)

where γ is a random complex numbe r. For almost all choices of a complex constant

γ, all solution paths deﬁned by the homotopy above are regular, i.e.: for all λ ∈

[0, 1], the Jacobian matrix of H(x, λ) is regular and no path diverges.

6-42 Types of linear homotopy

As we have seen, the start system can be constructed intuitively, reducing the

original system (target system) to a more simple system (start system), whose

roots can be easily computed. In order to obtain all roots of the target sys tem, the

start system should have as many roots as the target system

. The start system

can be constructed in many ways, however there are two typical types of the start

systems which are usually employed.

6-421 Fixed point homotopy

The start system can be considered as

p(x) = x − x

(6.24)

where x

is a guess value for the root of the target system q(x) = 0. In this case,

the homotopy function is

H(x, λ) = (1 − λ) (x − x

) + λq(x). (6.25)

6-422 Newton homotopy

Another construction for the start system is to consider p(x) as

p(x) = q(x) − q(x

). (6.26)

In this case the homotopy function is

Remark: However, there are certain theorems that place smoothness restrictions on

the input functions, under which all solutions of the target system are found. See [9]

72 6 Linear homotpy

H(x, λ) = (1 − λ)(q(x) − q(x

)) + λq(x) (6.27)

H(x, λ) = q(x) − (1 − λ)q(x

). (6.28)

Although the Newton homotopy is one of the easiest homotopies to use, one

does not have guarantees that all solutions will be found, see [109]. There are

other methods to construct start systems for linear homotopy. In the following

section, we shall see how one can deﬁne a start system for polynomial systems

automatically.

6-423 Start system for polynomial systems

A fundamental question is, how can we ﬁnd the proper start system, which will provide

all solutions of the target system ? This problem can be solved if the nonlinear system

is specially a system of polynomial equations.

Let us consider the case where we are looking for the homotopy solution of

f(x) = 0, where f (x) is a polynomial system, f(x) : R

→ R

. To get all solutions,

one should ﬁnd a proper polynomial system as the start system, g(x) = 0, where

g(x) : R

→ R

with known and easily computable solutions. An appropriate start

system can be generated in the following way, see [215].

Let f

, . . . , x

), i = 1, . . . , n be a system of n polynomials. We are interested

in the common zeros of the system, namely f = (f

(x), . . . , f

(x)) = 0. Let d

denote the degree of the j

polynomial - that is the degree of the highest order

monomial in the equation. Then such a starting system is,

(x) = e

iφ



−



iθ





= 0, j = 1, . . . , n (6.29)

where φ

and θ

are random real numbers in the interval [0, 2 π] and here i is

the imaginary value. If no random complex numbers are introduced for the initial

values, this may lead to singularity in the Jacobian of the Newton’s method. The

equation above has the obvious particular solution x

= e

iθ

and the complete set

of the starting solutions for j = 1, . . . , n is given by



2πk



, k = 0, 1, . . . , d

− 1. (6.30)

Bezout’s theorem, see [249], states that the number of isolated roots of such a

system is bounded by the total degree of the system, d = d

···d

. We illustrate

the discussion above by means of Example 6.1. However, we should mention, that

there is a tighter upper bound for the number of the solutions introduced as the

BKK-bound (due to contributions by Bernstein, Khovanskii and Kushnirenko) and

using “mixed volumes”, see [74, 75]. For dense systems, i.e., if all monomials have

non-zero coeﬃcients, this quantity gives us back the Bezout bound, whereas in

many other cases it might b e much smaller.

6-4 Solving nonlinear equations via homotopy 73

Example 6.1. Let us consider the following system

(x, y) = x

+ y

− 1 (6.31)

(x, y) = x

+ y

− 1. (6.32)

With the degree s of the polynomials being d

= 2 and d

= 3, this system has six

pairs of roots (i.e., d

= 2×3 = 6) listed in Table 6.3 resulting from the direct solution.

Table 6.3. Roots of system Eqs. (6.31)-(6.32)

x y

0 1

1 0

−1 −

√

−1 +

√

−1 +

√

−1 −

√

Now we compute a start system and its solutions by considering equations (6.29) and

(6.30) with n = 2 and x

= x, and x

= y, the resulting start system consisting of two

equations. Employing Eq (6.29), the ﬁrst equation is

(x, y) = e

iφ

−



iθ



) (6.33)

or in its trigonometric form

(x, y) = (cos φ

+ i sin φ

)



− (cos θ

+ i sin θ

)



(6.34)

which can be simpliﬁed as

(x, y) =



− cos 2θ

− i sin 2θ



(cos φ

+ i sin φ

) (6.35)

Generating two real random numbers, θ

and φ

in the interval [0, 2 π], we may get

(x, y) = (0.673116 + 0.739537i)



−0.933825 + 0.35773i + x



. (6.36)

The second equation can be generated in the same way with randomly generated real

numbers, θ

and φ

(x, y) = (−0.821746 − 0.569853i)



−0.957532 −0.288325i + y



. (6.37)

The ﬁrst equation has the following roots, considering Eq (6.30) with d

= 2

= e

(

2π0

)

= 0.983317 −0.1819i, (6.38)

and

74 6 Linear homotpy

= e

(

2π1

)

= −0.983317 + 0.1819i. (6.39)

Similarly, the second equation has three roots, d

= 3

= e

(

2π0

)

= −0.413328 −0.910582i (6.40)

= e

(

2π1

)

= 0.995251 + 0.0973382i (6.41)

= e

(

2π2

)

= −0.581923 + 0.813244i. (6.42)

All combinations of these roots {x

, y

} are the roots of the start system,

, y

} = {0.983317 −0.1819i, −0.413328 − 0.910582i} (6.43)

, y

} = {0.983317 −0.1819i, 0.995251 + 0.0973382i} (6.44)

, y

} = {0.983317 −0.1819i, −0.581923 + 0.813244i} (6.45)

, y

} = {−0.983317 + 0.1819i, −0.413328 − 0.910582i} (6.46)

, y

} = {−0.983317 + 0.1819i, 0.995251 + 0.0973382i} (6.47)

, y

} = {−0.983317 + 0.1819i, −0.581923 + 0.813244i} (6.48)

The homotopy function is given by

H(x, y, λ) = (1 − λ)



(x, y)



+ λ



(x, y)



, (6.49)

and the corresponding diﬀerential equation system

dλ



x(λ)

y(λ)



= −H

−1

x,y

(6.50)

where

x,y

∂f

∂x

+ (1 − λ)

∂g

∂x

∂f

∂y

+ (1 − λ)

∂g

∂y

∂f

∂x

+ (1 − λ)

∂g

∂x

∂f

∂y

+ (1 − λ)

∂g

∂y

(6.51)

and



(x, y) − g

(x, y)

(x, y) − g

(x, y)



. (6.52)

Hence, we must solve this system with six initial values. These initial values - the

solutions of the start system - will provide the start points of the six homotopy paths.

The end points of these paths are the six desired solutions of the original system f

= 0

and f

= 0. In this case, the trajectories of the solution of the system of diﬀerential

equations, Eq (6.50) will be complex. The curves in Fig. 6.8. shows the homotopy paths

belonging to the six initial values given by, Eq (6.43) - Eq (6.48). The curves show the

paths on the complex plane, where axis Re stands for the real and axis Im stands for

the imaginary parts of a complex number. The parameter value λ is increasing along the

path from the solution of the start system, λ = 0 up to the solution of the target system,

λ = 1, the end point of the curve. Along the paths the homotopy function is H = 0 for

all λ. The end points of the homotopy paths are listed in Table 6.4