Atkinson K. An Introduction to Numerical Analysis
Подождите немного. Документ загружается.


FINITE
DIFFERENCES
AND
TABLE-ORIENTED INTERPOLATION
FORMULAS
147
directly,
=
Limitf[x,x
0
,
..•
,xn,x+h]
h-+0
=
j[x,
Xo,
X1•···•
Xn,
x]
d
-j[x
0
,x
1
,
•••
,xn,x]
=J[x
0
,x
1
,
•.•
,xn,x,x]
dx
(3.2.17)
The existence and continuity of the right-hand side
is
guaranteed using (3:2.13).
There
is
a rich theory involving polynomial interpolation and divided differ-
ences, but
we
conclude at this point with one final straightforward result.
If
f(x)
is
a polynomial of degree m, then
_ ( polynomial of degree
m - n - 1
f[xo····•xn,x]-
am
0
n < m
-1
n =
m-
1 (3.2.18)
n > m
-1
where
f(x)
=
amxm
+lower
degree terms. For the proof,
see
Problem 14.
3.3 Finite Differences
and
Table-Oriented
Interpolation Formulas
In this section,
we
introduce forward and backward differences, along with
interpolation formulas that
use
them. These differences are referred to collec-
tively as
finite differences, and they are used to produce interpolation formulas
for tables in which the abscissae
{X;}
are evenly spaced. Such interpolation
formulas are also used in the numerical solution of ordinary and partial differen-
tial equations. In addition, finite differences can be used to determine the
maximum degree of interpolation polynomial that can be used safely, based
o.n
the accuracy of the table entries. And finite differences can be used to detect
noise in data, when the noise
is
large with respect to the rounding errors or
uncertainty errors of physical measurement. This idea
is
developed in Section 3.4.
For a given
h >
0,
define
!::.hf(z)
=
f(z
+h)-
f(z)
Generally the h
is
understood from the context, and
we
write
Af(z)
=
f(z
+h)-
f(z)
(3.3.1)

148 INTERPOLATION THEORY
This quantity
is
called the forward difference of f
at
z,
and
b.
is
called the
forward difference operator. We will always be working with evenly spaced node
points
X;
= x
0
+ ih, i = 0, 1,
2,
3,
....
Then we write
or
more concisely,
(3.3.2)
For
r
~
0,
define
IJ..'+
1
f(z)
= b..'f(z
+h)-
D!f(z)
(3.3.3)
with
!::..
0
f(z)
=
f(z).
The term D!f(z)
is
the
rth-order
forward difference
off
at
z.
Forward differences are quite easy to compute,
and
examples are given later in
connection with
an
interpolation· formula.
We first derive results for the forward difference operator by applying the
results on the
Newton
divided difference.
Lemma I
For
k
~
0,
(3.3.4)
Proof
For
k = 0, the result
is
trivially true.
For
k =
1,
f1-
fo
1
f[x
0
,
x
1
]
= =
-h
b..fo
xt-
Xo
which shows (3.3.4). Assume the result (3.3.4) is true for all forward
differences
of
order
k.::;;
r. Then for k = r + 1, using (3.2.7),
Applying the induction hypothesis, this equals
I
!J..'+
IJr.
(r
+
l)!hr+l
n
•
We now modify the Newton interpolation formula (3.2.9) to a formula
involving forward differences in
place·
of
divided differ.ences. For a given value of
x
at
which we will evaluate the interpolating polynomial, define
X - x
0
!J.=--
h

FINITE
DIFFERENCES
AND TABLE-ORIENTED INTERPOLATION FORMULAS
149
to indicate the position of x relative
to
x
0
.
For example,
p.
=
1.6
means
xis
6j10
of the distance from x
1
to x
2
.
We
need a formula for
with respect to the variable
p.:
x-
xj
= x
0
+
p.h-
(x
0
+
jh)
=
(p.-
j)h
(x-
x
0
) • • •
(x-
xk)
=
p.(p.-
1)
· · ·
(p.-
k)hk+l
(3.3.5)
Combining (3.3.4) and (3.3.5) with the divided difference interpolation formula
(3.2.9),
we
obtain
!lfo
!1%
Pn(x) =
fo
+
p.h
·-
+
p.(p.-
1)h
2
• -
2
h 2!h
t;.nJ;
+
..
·
+p.(p.-
1)
..
·
(p.-
n +
l)hn
· -
0
n!hn
Define the binomial coefficients,
(
}-t)
=
p.(p.-
1)
...
(p.-
k +
1)
k
k!
k>O
and (
~)
=
1.
Then
X-
Xo
p.=
h
This is the Newton forward difference form
of
the interpolating polynomial.
Table 3.6
Fonnat for constructing forward differences
X;
/;
f./;
t,.2ji
f.3/;
Xo
fo
f.Jo
xl
ft t.
2
fo
t.jl
t.
3
fo
x2
/2
t,.2jl
t.j2
t,.3jl
XJ
/3
t,.2j2
t.j3
t,.3j2
x4
!4
t,.2j3
t.j4
xs
fs
(3.3.6)
(3.3.7)

150
INTER
PO
LA
T!ON
THEORY
Table 3.7 Forward difference table
for-
f(x)
=
Vx
x,
/;
!:J.j,
t:J.2/,
2.0 1.414214
.034924
2.1
. 1.449138
-.000822
.034102 .000055
2.2 1.483240
-;-.000767
-.000005
.033335 .000050
2.3
1.516575
-.000717
.032618
2.4 1.549193
Example
For
n =
1,
P!(x)
=
fo
+
p.t..fo
(3.3.8)
This is the formula that most people use when doing linear interpolation
in
a
table.
For
n = 2,
(3.3.9)
which is
an
easily computable form
of
the quadratic interpolating polynomial.
The
forward differences are constructed in a pattern like that for divided
differences,
but
now there are no divisions (see Table 3.6).
Example
The
forward differences for
f(x)
=
Vx
are given in Table 3.7. The
values
of
the interpolating polynomial
will
be the same
as
those obtained using
the
Newton
divided difference formula, but the forward difference formula (3.3.7)
is much easier
to
compute.
Example Evaluate Pn(x) using Table 3.7 for n =
1,
2,
3,
4,
with x = 2.15. Note
that
v'2.15 = 1.4662878; and
p.
=·1.5.
p 1
(X)
= 1.414214 + 1.5( .034924) = 1.414214 + 0.52386 = 1.4666
(1.5)(
.5)
P2
(X)
= p 1 (X) + 2 ( - .000822) = 1.4666 - .00030825 = 1.466292
(1.5)(
.5)(-
.5)
P3
(X)
=
P2
(X) + 6 ( .000055) = 1.466292 - .0000034
= 1.466288
( )
-
()
<
1
-
5
)(.
5
)(-
·
5
)(-
15
)(-
000005)-
1.466288-
.00000012
P4
X - P3 X + 24 . -
= 1.466288

ERRORS IN DATA AND FORWARD DIFFERENCES
151
The correction terms are easily computed; and by observing their
size,
you obtain
a generally accurate idea of when the degree
n is sufficiently large. Note that the
seven-place accuracy in the table values of
Vx
leads to at most one place of
accuracy in the forward difference
6.
4
/
0
•
The forward differences of order greater
than three are almost entirely the result of differencing the rounding errors in the
table entries; consequently, interpolation in this table should be limited to
polynomials of degree
less
than four. This idea
is
given further theoretical
justification in the next section.
There are other
forms· of differences and associated interpolation formulas.
Define the
backward difference by
'V/(z) =
f(z)-
f(z-
h)
\l'+
1
f(z)
=
\l:f(z)-
'V'i(z- h)
r
?:.
1
(3.3.10)
Completely analogous results to those for forward differences can be derived.
And
we
obtain the Newton backward difference interpolation formula,
Pn(x) =
fo
+ (
~")vfo
+ (
-p/
1
)'V%
+ · · · + (
-p
\n-
1
)'Vn/
0
(3.3.11)
In this formula, the interpolation nodes are x
0
,
x_
1
,
x_
2
,.
:.
, x
-n>
with
x_j
=
x
0
-
jh,
as
before. The value P
is
given
by
Xo-
X
p=---
h
reflecting the fact that x will generally be
less
than x
0
when using this formula.
A backward difference diagram can be constructed in an analogous way
to
that
for forward differences. The backward difference formula
is
used in Chapter 6 to
develop the Adams family of formulas (named after John Couch Adams, a
nineteenth-century astronomer) for the numerical solution of differential equa-
tions.
Other difference formulas and associated interpolation formulas can be given.
:Smce
they are used much
less
than the preceding formula,
we
just refer the reader
to Hildebrand (1956).
3.4
Errors
in Data
and
Forward
Differences
We can use a forward difference table to detect noise in physical data, as long
as
the noise
is
large relative
to
the usual limits of experimental error. We must begin
with some preliminary lemmas.

152 INTERPOLATION THEORY
Proof
/(r)(~)
"'f=h''J[
]-h'l
i
-h'j(r)(t)
u;;
r.
x,.,
..
. ,
xi+r
-
r.
-
s;
r!
using Lemma 1 and
(3.2.12).
Lemma
3
For
any
two
functions f and
g,
and for any two constants a and
/3,
tl'(af(x)
+ /3g(x)) =
atl'f(x)
+ f3tl'g(x) r
~
0
Proof The result
is
trivial if r = 0 or r =
1.
Assume the result
is
true
for
all
r.::;;
n, and prove it for r = n +
1:
tln+l[af(x) + f3g(x)] =
tln[af(x
+h)+
f3g(x
+h)]
-tln[af(x)
+ f3g(x)]
= atlnf(x
+h)+
f3tlng(x
+h)
-atlnf(x)-
f3tlng(x)
using the definition (3.3.3) of
tln+I
and the
ind~ction
hypothesis. Then
by recombining,
we
obtain
a[tlnf(x
+h)-
tl"f(x)] + f3[tl"g(x
+h)-
tl"g(x)]
= atl"+Y(x) +
f3tln+Ig(x)
Lemma 2 says that if the derivatives of
f(x)
are bounded, or if they do not
increase rapidly compared with
h-",
then the forward differences tlnf(x) should
become smaller
as
n increases.
We
next look at the effect of rounding errors and
other errors
of
a larger magnitude than rounding errors. Let
f(x,.) =
[;
+ e(x,.)
i=0,1,2,
...
(3.4.1)
with
[; a table value that
we
use
in
constructing the forward difference table.
Then
tl'i; = tlrf(x;) - Li'e(x;)
=
h'f(r)(~;)
- tl'e(x,.)
(3
.4.2)
The first term becomes smaller
as
r increases,
as
illustrated in the earlier forward
difference table for
f(x)
=/X.
To
better understand the behavior of
tlre(x,.
),
consider the simple case in
which
.
e(x,.) =
{~
i
=I=
k
i = k
(3.4.3)

ERRORS IN DATA AND FORWARD DIFFERENCES 153
Table 3.8 Forward differences of error function
e(x)
X;
e(x;)
toe(x;)
t.
2
e(x;)
t.
3
e(x;)
0 0
xk-2
0 0
0
(
xk-1
0
(
-3c
xk
(
-2c
-(
3c
xk+l
0
(
0
-(
xk+2
0
0
0
The forward difference of this function are given in Table
3.8.
It can be proved
that the column for
t{e(x;)
will
look like
(3.4.4)
Thus the effect of a single rounding error
will
propagate and increase in value as
larger order differences are formed.
With rounding errors defining a general error function as in
(3.4.1), their effect
can be looked upon
as
a sum of functions of the form (3.4.3). Since the values of
e(x;)
in general will vary in sign and magnitude, their effects
will
overlap in a
seemingly random manner. But their differences will still grow in
size,
and the
higher order differences of table values
i;
will
eventually become useless. When
differences
!::.'!;
begin to increase in
size
with increasing
r,
then these differences
are most likely dominated by rounding errors and should not be used. An
interpolation formula of degree less than
r should be used.
Detecting noise
in
data This same analysis can be used to detect and correct
isolated errors that are large relative to rounding error. Since
(3.4.2) says that the
effect
of
the errors will eventually dominate,
we
look for a pattern like (3.4.4).
The general technique
is
illustrated in Table
3.9.
From (3.4.2)
!::.'e(x;)
= !::.'f(x;)-
!::.'[
Using r = 3 and one of the error entries chosen arbitrarily, say the first,
( = -
.00002
- (
.00006)
= - .00008
Try this to see how it will alter the column of
t::.'f
(see Table 3.10). This will not
be improved on by another choice of
t:, say £ =
-.00007,
although the results
154
INTERPOLATION
TI-IEORY
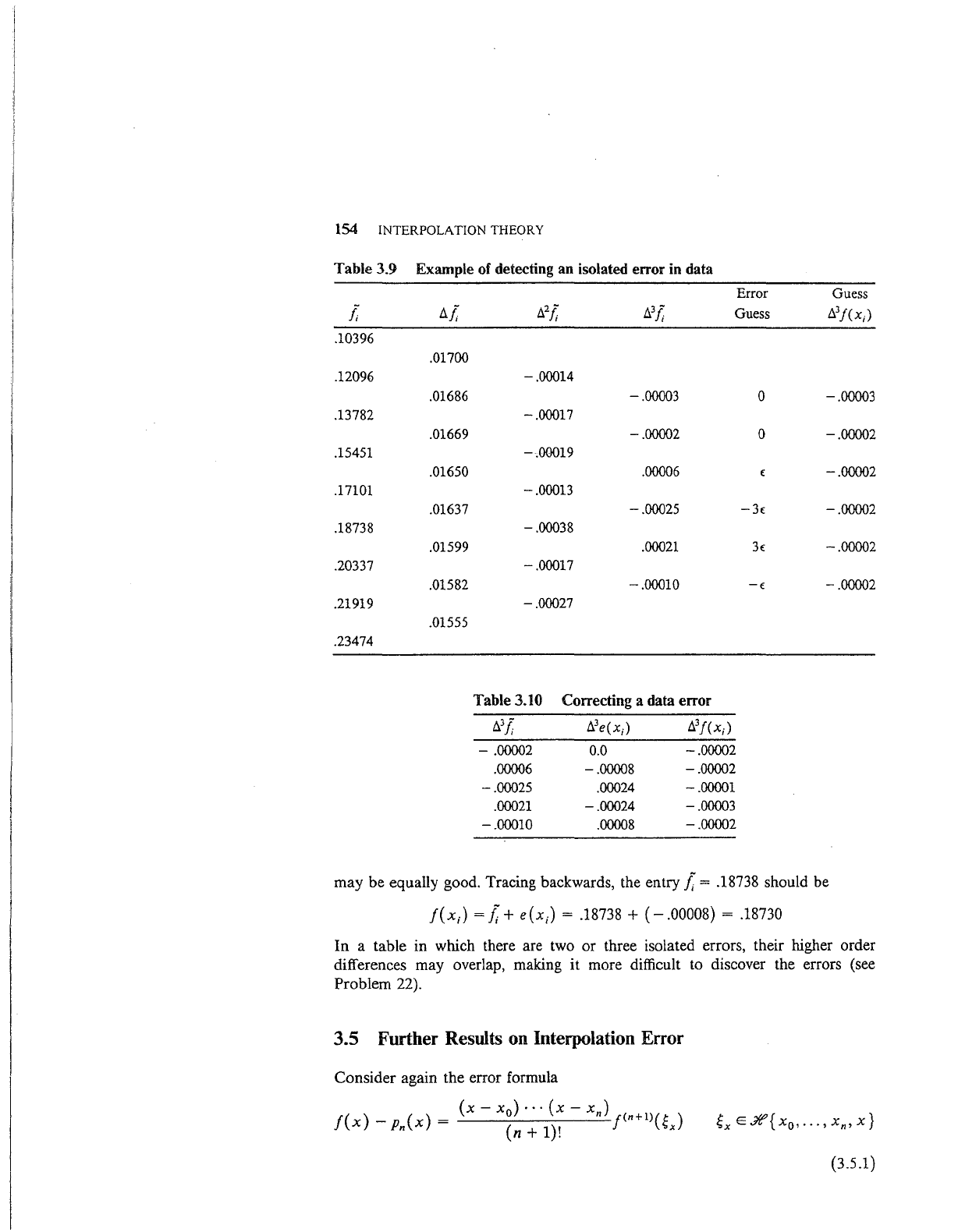
Table3.9
Example of detecting an isolated
error
in data
Error
Guess
i
t:.i
t:,.2j;
t:,.3j;
Guess
t:,.3j(x;)
.10396
.01700
.12096
-.00014
.01686
-.00003
0 -.00003
.13782
-.00017
.01669
-.00002
0
-.00002
.15451
-.00019
.01650
.00006
-.00002
.17101
-.00013
.01637
-.00025
-3(
-.00002
.18738
-.00038
.01599
.00021
3€
-.00002
.20337
-.00017
.01582
-.00010
-(
-.00002
.21919
-.00027
.01555
.23474
Table 3.10 Correcting a data
error
t:,.3j;
t:.
3
e(x;)
t:,.3j(x;)
-.00002
0.0
-.00002
.00006
-.00008
-.00002
-.00025
.00024
-.00001
.00021
-.00024
-.00003
-.00010
.00008
-.00002
may be equally good. Tracing backwards, the entry i; = .18738 should be
f(x;)
= i; + e(x;) = .18738 +
(-
.00008) = .18730
In a table in which there are two or three isolated errors, their higher order
differences may overlap, making it more difficult
to
discover the errors (see
Problem 22).
3.5 Further Results on Interpolation Error
Consider again the error formula
(3.5.1)

FURTHER RESULTS
ON
INTERPOLATION ERROR
155
We assume that
j(x)
is
n + 1 times continuously differentiable on an interval I
that contains
£'{x
0
,
••.
,
xn,
x} for all values x
of
interest. Since
gx
is
unknown,
we
must replace j<n+ll(gx) by
cn+t
= MaxiJ<n+t>(t)l
tEl
(3.5.2)
in order to evaluate (3.5.1). We will concentrate our attention on bounding the
polynomial
'(3.5.3)
Then from (3.5.1), for
cn+l
Maxlf(x)-
Pn(x)l
~
( ) Maxl'l'n(x)l
xel
n + 1 !
xe/
(3.5.4)
We will consider only the use of evenly spaced nodes:
x
1
= x
0
+
jh
for
j =
0,
1,
...
, n. We first consider cases of specific values of n, and later
we
comment
on
the
"case
of general n.
Case
1 n = 1.
'l'
1
(x)
=
(x-
x
0
)(x-
x
1
).
Then easily
h2
Max l'l'l(x)l = -
Xo,X.:SX
1
4
See Figure 3.2 for an illustration.
Case 2 n =
2.
To
bound
'l'
2
(x)
on [x
0
,
x
2
],
shift it along the x-axis to obtain
an equivalent polynomial
ir
2
(x)
=
(x
+
h)x(x-
h)
whose graph is shown in Figure 3.3. Its shape
and
size are exactly the same
as
with the original polynomial 'lt
2
(x), but it is easier to bound analytically. Using
y
Figure3.2 y =
'l'
1
(x).
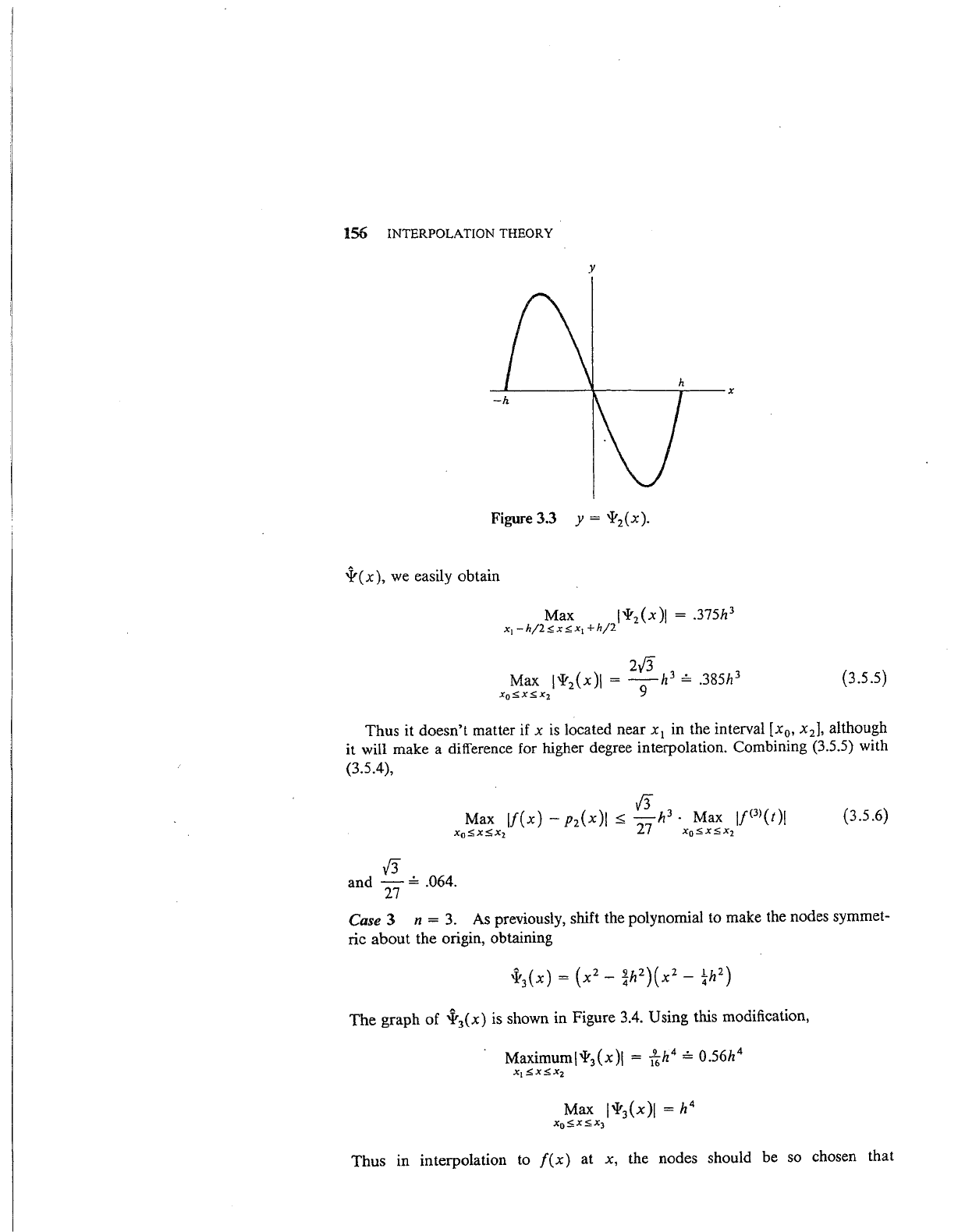
156 INTERPOLATION THEORY
y
Figure
3.3 y = 'l'
2
(x).
-}(x), we easily obtain
Max
l'l'
2
(x)l = .375h
3
x
1
-hj2,;x,;x
1
+h/2
(3.5.5)
Thus
it doesn't matter if x
is
located near x
1
in the interval [x
0
,
x
2
],
although
it will make a difference for higher degree interpolation. Combining (3.5.5) with
(3.5.4),
f3
Max
lf(x)-
p
2
(x)l
~
-h
3
•
Max
IJ(3>(t)l
x
0
:;;x5,x
2
27 x
0
,;x,;x
2
f3
and-=
.064.
27
(3.5.6)
Case 3 n = 3. As previously, shift the polynomial to make the nodes symmet-
ric
about
the origin, obtaining
The
graph
of
-}
3
{x) is shown in Figure 3.4. Using this modification,
Maximuml'l'
3
(x)l = ft;h
4
= 0.56h
4
x
1
,;x,;x
2
Max
l'l'
3
(x)l = h
4
x
0
=s;x.s;x
3
Thus
in interpolation to
f(x)
at x, the nodes should be so chosen that
