ASM Metals HandBook Vol. 8 - Mechanical Testing and Evaluation

Подождите немного. Документ загружается.

Fatigue Testing of Brittle Solids

J.A. Salem, Glenn Research Center at Lewis Field; M.G. Jenkins, University of Washington

Strength-Based Test Methods

Strength-based methods or “indirect” methods employ smooth test specimens, such as flexural beams or tensile

specimens, and estimate fatigue properties from strengths measured over different time intervals. Strength-

based methods directly sample the flaw distribution within or on the surface of the test specimens. The cracks

thus develop from at least some of the same sources as in a component of the same material. However, the

results are subject to the scatter inherent in the strength distribution of the material, and thus a relative large

number of tests are required. Further, strength-based methods do not measure the actual crack size but infer it

from the measured strength.

Three basic strength test methods and accompanying analytical relations have been developed for determining

the fatigue parameters and behavior of ceramics and glasses: static loading, dynamic loading, and cyclic

Static Loading. Typically, tensile specimens or flexure specimens (e.g., beams or plates) are subjected to a

constant load in the environment of interest. The time-to-failure and the applied stress are recorded and used to

determine the fatigue parameters according to any of the Eq 1, 2, 3, 4, and 5. The generalized slow crack

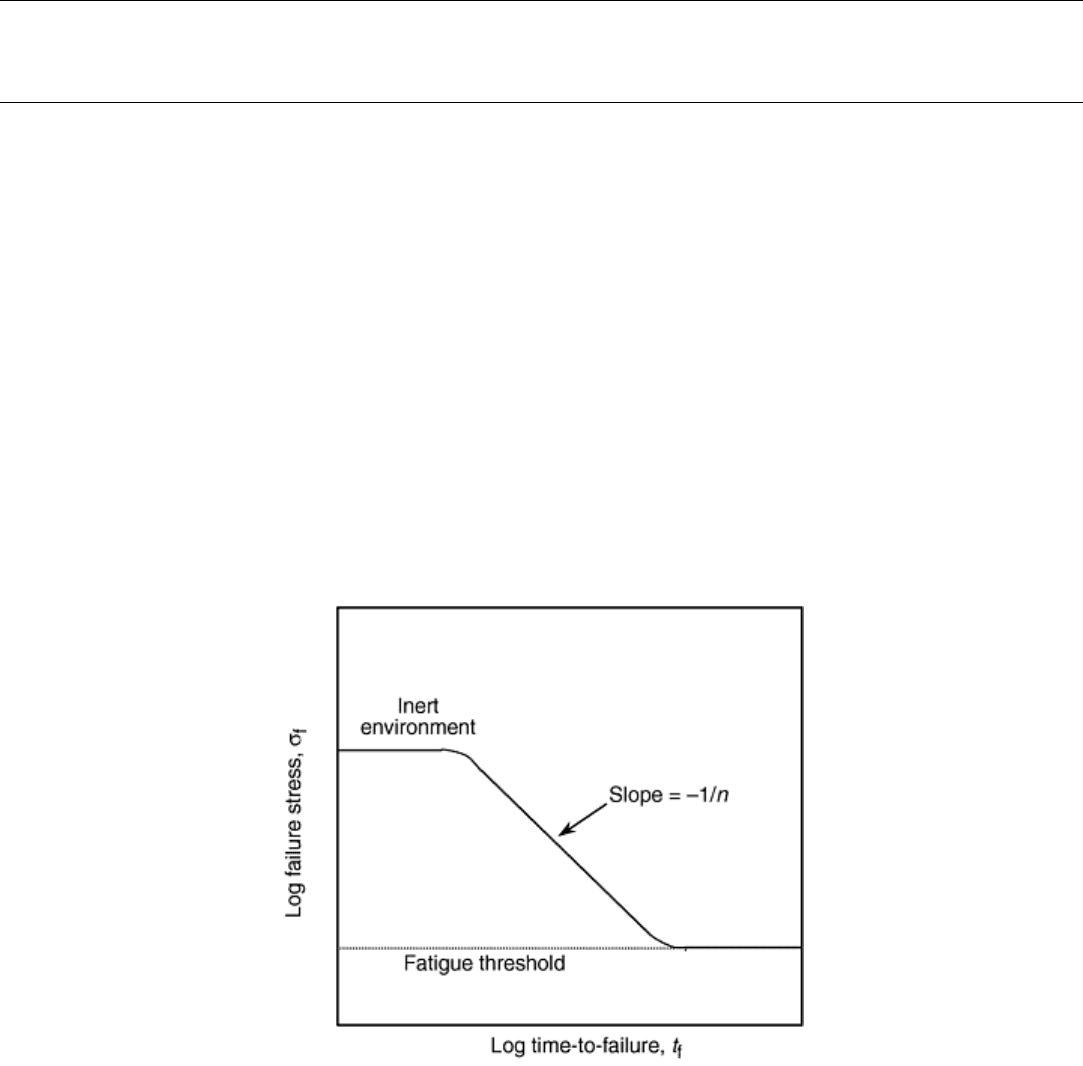
growth behavior for static loading is shown in Fig. 2.

Fig. 2 Generalized failure stress as a function of time-to-failure on a logarithmic scale for ceramics and

glasses exhibiting environmentally induced slow crack growth

One test method, Japanese Industrial Standard (JIS) 1632 “Test Methods for Static Bending Fatigue of Fine

Ceramics,” has been standardized for the determination of fatigue strength by static loading (Ref 18) at room or

elevated temperatures. The standard gives guidance on the test method but not in the calculation of fatigue

parameters such as A and n.

Uniaxial flexural test specimens are manufactured and tested in three- or four-point loading in accordance with

JIS R 1601, “Test Method for Flexural Strength (Modulus of Rupture) of Fine Ceramics” (Ref 56). The use of

at least three stress levels is recommended, and the breaking times at one of the stress levels must be distributed

between 0 and 100 h, minimum. No requirement on the number of test pieces is specified; however, three tests

per stress level are recommended. Tests may be stopped after 100 h if failure has not occurred. An initial

fatigue stress equal to 75% of the fracture strength is used. Subsequent stresses differing by 5 to 10% from the

initial fatigue load are applied, depending on the initial time-to-failure and scatter in the data. An example of

failure stress data as a function of the failure time is shown in Fig. 3 (Ref 18).

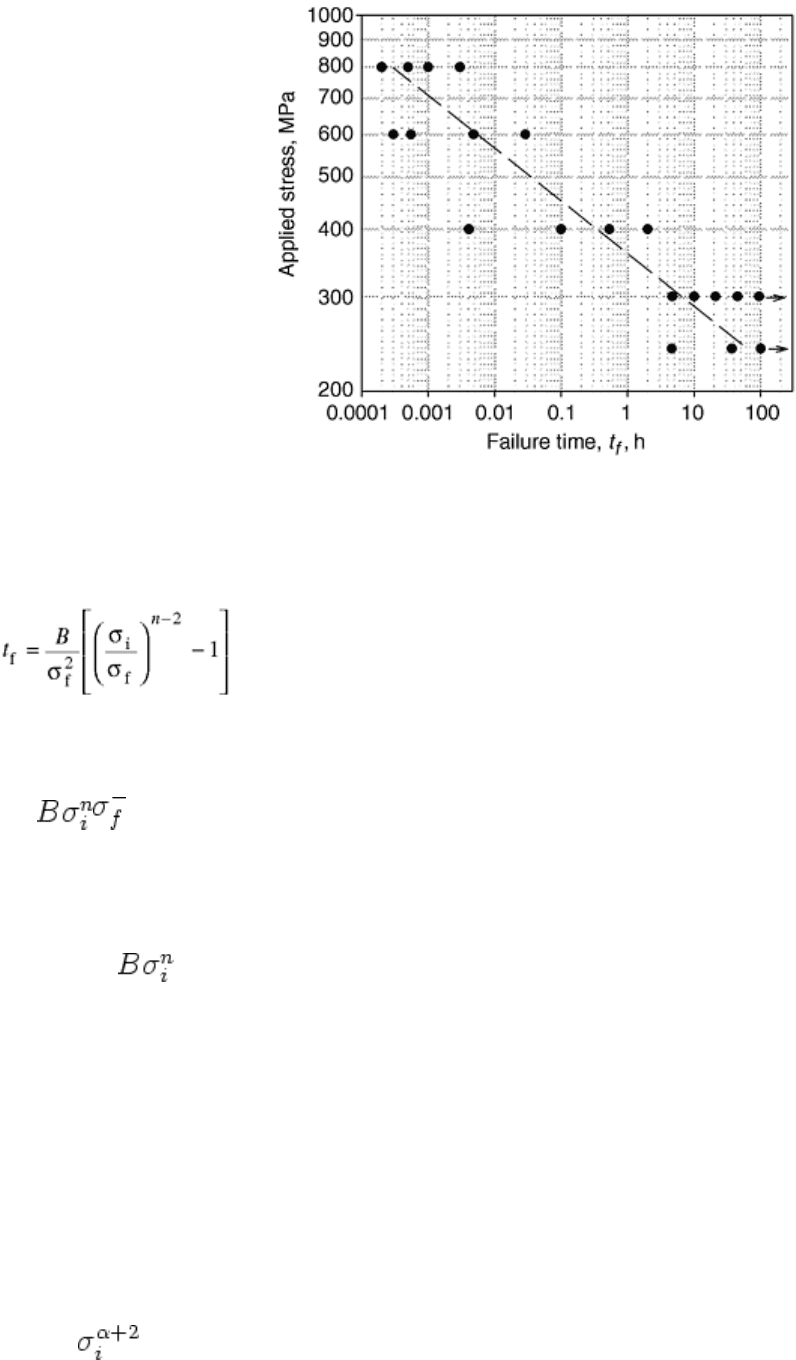
Fig. 3 Example of failure stress as a function of time-to-failure on a logarithmic scale for ceramics and

glasses exhibiting environmentally induced slow crack growth. Adapted from Ref 18

The stress at fracture or fatigue strength σ

, is related to the time-to-failure, t

, by (Ref 43, 57, and 58):

(Eq 7)

where B is a parameter associated with A, n, fracture toughness, crack geometry, and loading configuration, and

is the “inert” strength or the strength under noncorrosive conditions for which no crack extension occurs. For

most ceramics and glass, n > 10 so that Eq 7 can generally be simplified to:

(Eq 8)

The fatigue parameter n can be determined from the slope of a log t

versus log σ

plot by writing Eq 8 as:

log t

= -n log σ

+ log D

(Eq 9)

where

log D = log( )

(Eq 10)

Once the slope and intercept of Eq 9 are estimated, the parameters n and D and the standard deviation SD

and

can be estimated by a Taylor series expansion of the random variable of interest (Ref 59):

n = -α

(Eq 11)

≈ SD

(Eq 12)

D = 10

(Eq 13)

≈ (ln 10)(SD

)(10

)

(Eq 14)

where α is the slope and β is the intercept estimated by linear regression of Eq 9. For some design codes, the

fatigue parameters B and A are necessary (Ref 60, 61, 62). The parameter B and the standard deviation can be

estimated from:

B = 10

(Eq 15)

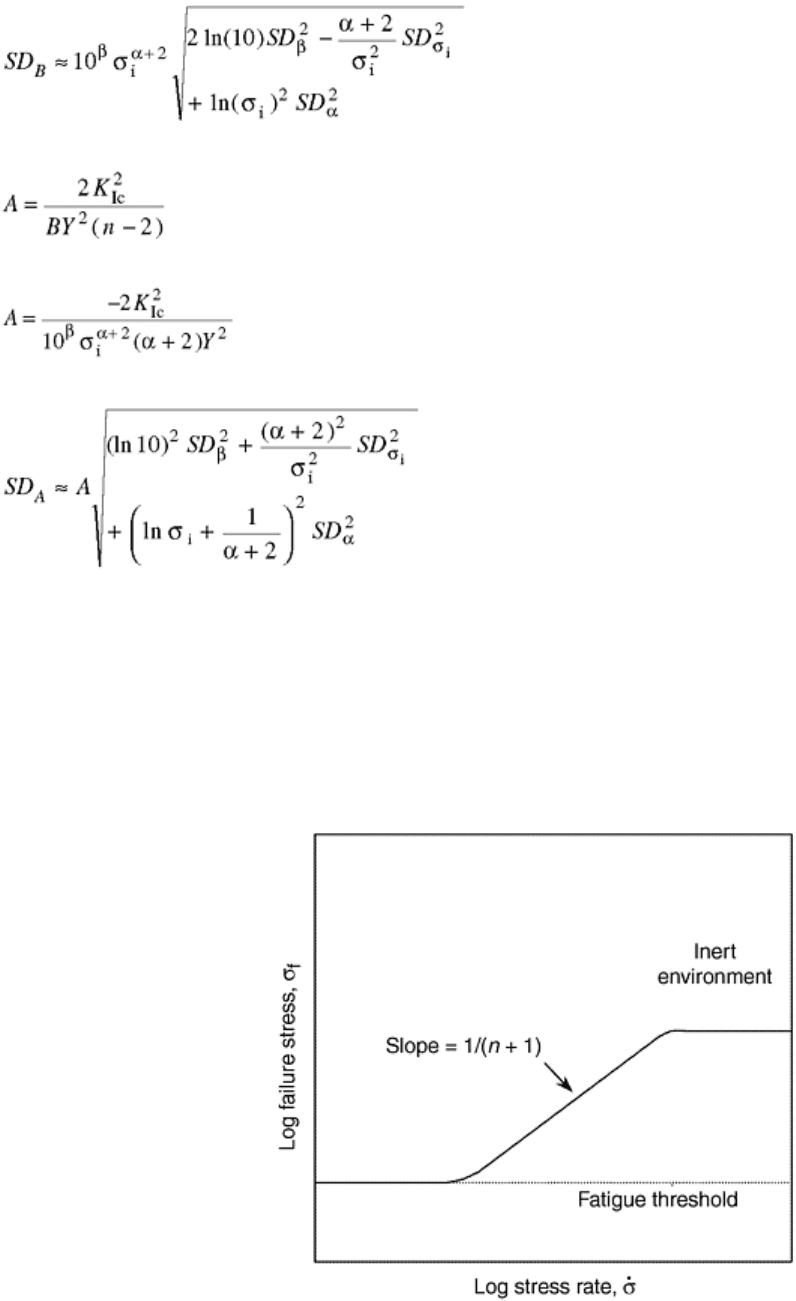
(Eq 16)

The parameter A in Eq 2 can be calculated from:

(Eq 17a)

(Eq 17b)

with

(Eq 18)

where Y is the stress-intensity factor coefficient and treated as a constant.

Note that plots of static fatigue data (e.g., Fig. 3) are usually made with the applied stress appearing as the

dependent variable; however, the dependent variable actually is the time-to-failure, and it must be minimized in

the regression analysis.

Dynamic Loading. Typically, tensile or flexure test specimens (e.g., beams or plates) are subjected to a constant

stress rate in the environment of interest. The failure stress and the applied stress rate are recorded and used to

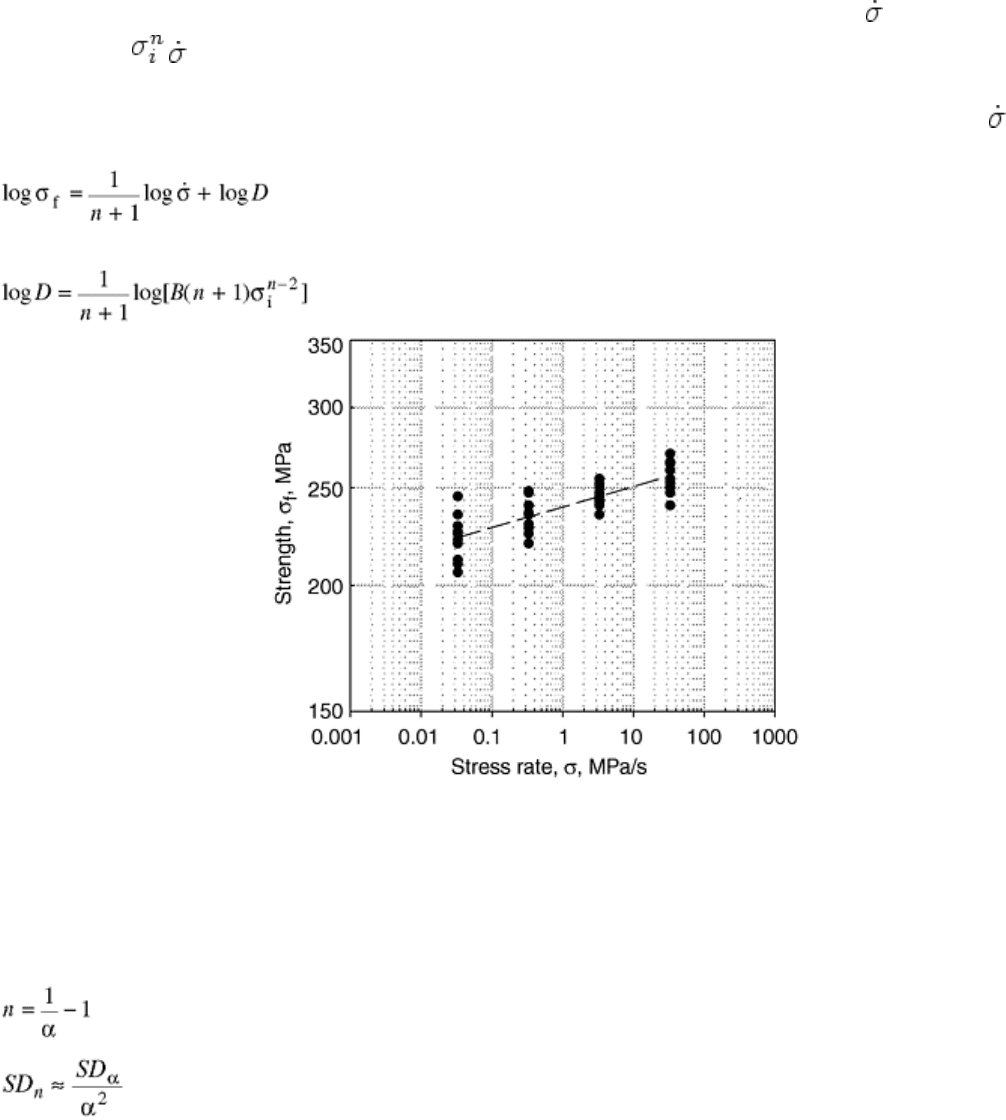
determine the fatigue parameters according to any of the Eq 1, 2, 3, 4, and 5. Figure 4 illustrates the observed

strength as a function of stress rate for dynamic loading. A detailed error analysis has been conducted for

dynamic loading (Ref 63).

Fig. 4 Generalized fracture strength as a function of stress rate on a logarithmic scale for ceramics and

glasses exhibiting environmentally induced slow crack growth

Two test methods have been standardized for the determination of fatigue strength by dynamic loading (Ref 15,

17). One standard (Ref 17), ASTM C 1368 “Standard Test Method for Determination of Slow Crack Growth

Parameters of Advanced Ceramics by Constant Stress-Rate Flexural Testing at Ambient Temperature” also

gives detailed guidance in the calculation of the fatigue parameter n, based on Eq 2. The standard uses uniaxial

flexural test specimens that are manufactured in accordance with ASTM C 1161 “Standard Test Method for

Flexural Strength of Advanced Ceramics at Ambient Temperature” (Ref 64) and tested in four-point flexure.

A total of 40 test specimen loaded at four stress rates that cover at least three orders of magnitude are required,

with a minimum of four tests at any of the rates. An example of failure stress data as a function of the stress rate

is shown in Fig. 5. The stress at fracture or fatigue strength, σ

, is related to the stress-rate, , by (Ref 57, 58):

= [B(n + 1) ]

1/n+1

(Eq 19)

where B is a parameter associated with A, n, fracture toughness, crack geometry, and loading configuration, and

is the inert strength. The fatigue parameter n can be determined from the slope of a log σ

versus log plot by

writing Eq 19 as:

(Eq 20)

where

(Eq 21)

Fig. 5 Example of failure stress as a function of stress rate on a logarithmic scale for ceramics and

glasses exhibiting environmentally induced slow crack growth. Adapted from Ref 17

The dependent variable is the fracture stress, and regression is performed to minimize fracture stress variation.

Once the slope and intercept of Eq 20 are estimated, the parameters n and D and the standard deviation SD

and

are estimated from:

(Eq 22)

(Eq 23)

D = 10

(Eq 24)

≈ (ln 10)(SD

)(10

)

(Eq 25)

where α and β are the slope and the intercept, respectively, estimated by linear regression of Eq 20. These

formulation follow a recently published standard (Ref 17) and provided values of n and D. For some design

codes, however, the parameters B and A are necessary (Ref 60, 61, and 62). The parameter B and the standard

deviation can be estimated from:

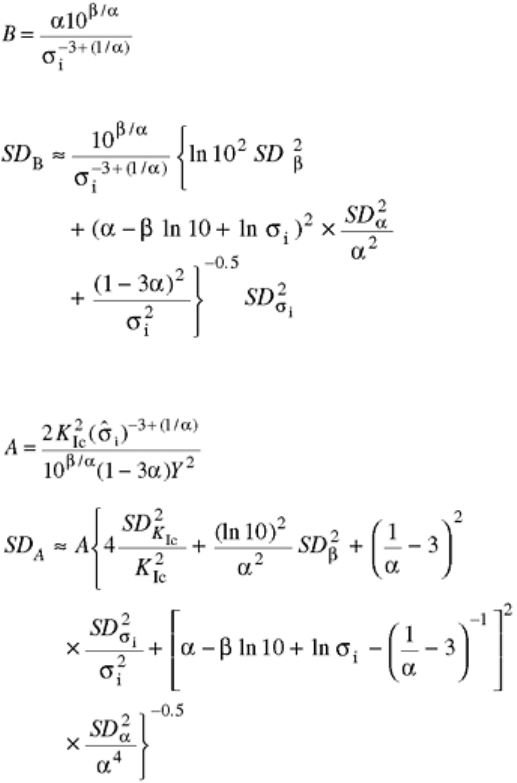
(Eq 26)

and

(Eq 27)

The parameter A corresponding to Eq 2 can be calculated from Eq 17aa or with the standard deviation of A

from:

(Eq 28)

(Eq 29)

In order to verify that the dynamic fatigue methodology is sufficiently robust for industrial use in the

development of design data, several round-robin test programs have been performed (Ref 65, 66, 67,and 68).

One round-robin involved dynamic fatigue testing of eight ceramic materials (Ref 65), with a given material

being tested by only one research institute and one manufacturer. A total of 30 specimens were tested in

distilled water at three to four stress rates ranging from 10

-2

to 10 MPa/s. In addition, the inert strength and

Weibull modulus were measured at 100 MPa/s. As Fig. 6 illustrates, good agreement occurred between the

research and industrial laboratories for materials with a low fatigue parameter, n, but poor agreement for

materials with a high fatigue parameter. It was believed that increasing the number of test specimens would

improve the results, as a single data point tended to have an unduly large effect on the slope for materials with

high n values.

Fig. 6 Round-robin results comparing fatigue parameters of various ceramics determined by using

dynamic loading. SSN, sintered silicon nitride; RBSN, reaction-bonded silicon nitride; ZTA, zirconia-

toughened alumina; HPSN, hot pressed silicon nitride. Source: Ref 66

A second round-robin tested alumina flexure specimens in distilled water (Ref 66, 67). The participants were

instructed to test 15 specimens in the as-received condition and 15 specimens with a 5 kg indentation. Most

participants covered less than two orders of magnitude in the stress rate, and the combined participant data

covered nearly five orders of magnitude. Figure 7 summarizes the fatigue parameters generated by the

participants for the as-received condition. Generally, the results improve as the number of specimens increases

from 15 to 33. However, even 33 test specimens can be inadequate. Most troublesome is the fact that the fatigue

parameter has been overestimated two out of three times. If the data points that appear to be outliers are

removed, a slight improvement results, as shown in Fig. 8. Although the final recommendations from the

round-robin were not published, the initial recommendations were that at least three orders of magnitude be

covered. Also, for testing at rates greater than 100 MPa/s, a piezoelectric load cell was recommended.

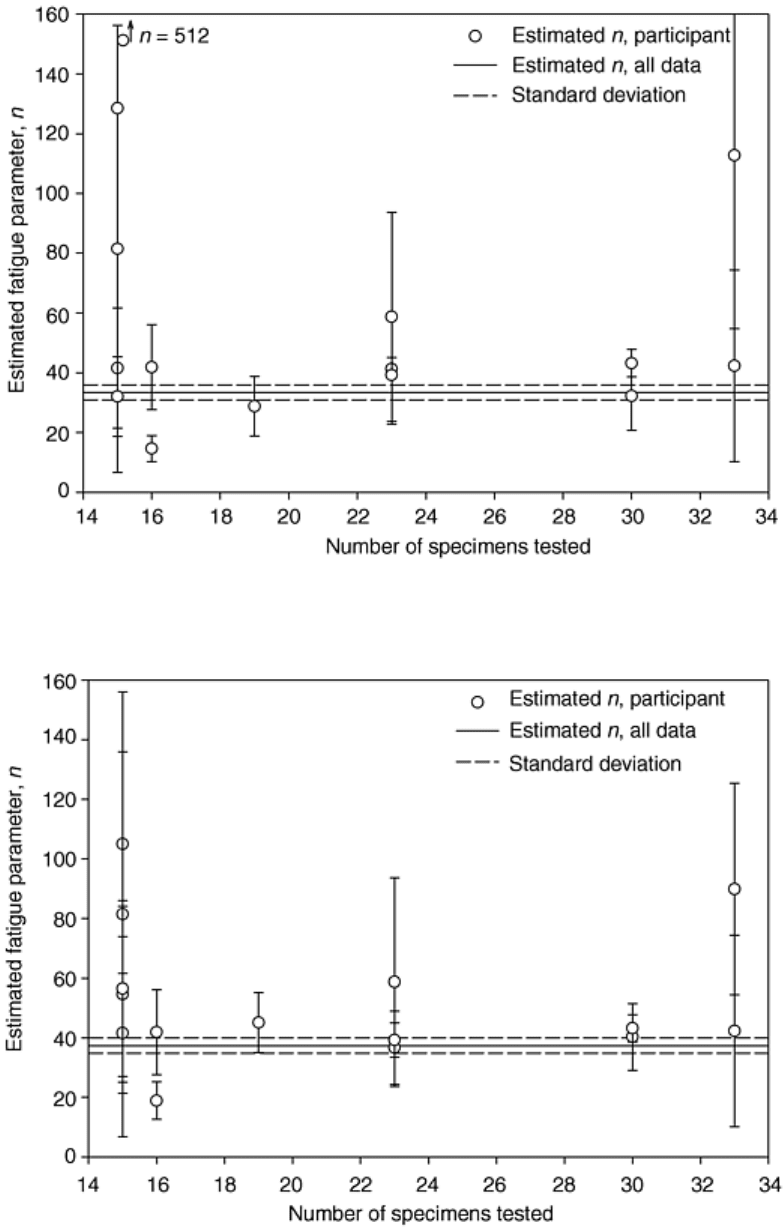
Fig. 7 Round-robin results comparing estimated fatigue parameters measured by dynamic loading of an

alumina in distilled water

Fig. 8 Round-robin results comparing estimated fatigue parameters for an alumina in distilled water.

Outlying data were censored.

The effect of the range of the stress rate can be seen in Fig. 9. If three orders of magnitude are covered, the

estimated value of n improves somewhat; however, more data are needed. It is not effective to increase the

number of tests without increasing the stress range. For example, one data set consisting of 33 tests measured

over 2.4 orders of magnitude still resulted in an estimated fatigue parameter three times greater than that for all

the data. Based on these results, it appears that at least 30 specimens and three orders-of-magnitude separation

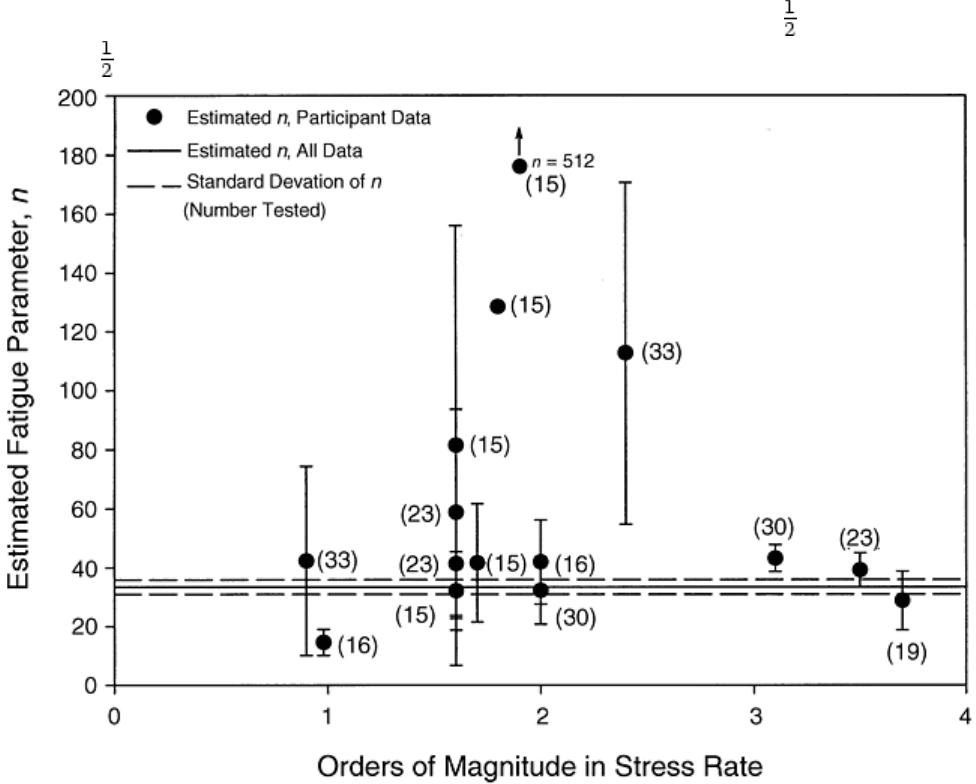
are required. Better results from a statistical viewpoint could be attained by testing of the specimens at the

lowest rate and at the highest rate (Ref 63).

Fig. 9 Round-robin results comparing estimated fatigue parameters for an alumina tested in distilled

water. Numbers in parentheses represent the number of specimens tested.

The round-robin results prompted the National Physical Laboratory to sponsor a follow-up, United Kingdom

only, round-robin (Ref 68). This led to another testing standard, ENV 843-3 “Determination of Subcritical

Crack Growth Parameters from Constant Stressing Rate Flexural Strength Tests” (Ref 15).

Cyclic Loading. Cyclic loading of ceramics and glasses has been performed for quite some time (e.g., Ref 1).

Initial results on glasses and materials with glass boundaries indicated little synergy of cycling on the life. Thus,

simpler test methods such as static and dynamic loading have generally been used, and the analysis adjusted to

account for load variation (Ref 45). However, as ceramics materials have been made less glasslike by

devitrification treatments and have been toughened by elongating the grain structure, transformation

toughening, or adding second phase particles, cyclic loading has been recognized as a significant issue (Ref 22,

23, 24, 25, 26, 27, 28, 29, 30, 31, and 32), and fatigue effects independent of the environment have been

measured.

Two testing methods have been standardized for the determination of cyclic fatigue strength of ceramics (Ref

16, 19). The standards focus on the method of data generation and give no guidance on how the data are to be

used. The two standards are somewhat complementary because one uses flexure of rectangular beam (Ref 16),

while the other uses uniaxial tension (Ref 19).

Test method JIS R 1621 “Testing Method for Bending Fatigue of Fine Ceramics” (Ref 16) recommends

applying a 20 Hz sinusoidal wave with an R-ratio of 0.1 to standard three- or four-point flexure configurations

(Ref 56). Other waveforms and frequencies are allowed. Three tests at three different maximum stress levels

that result in specimen fracture before 10

cycles are recommended. If three tests in a row result in lives greater

than 10

cycles, the remaining tests are conducted at a higher stress. The initial stress level is based on the

monotonic strength of the materials as measured with the same specimen and testing configuration. Testing can

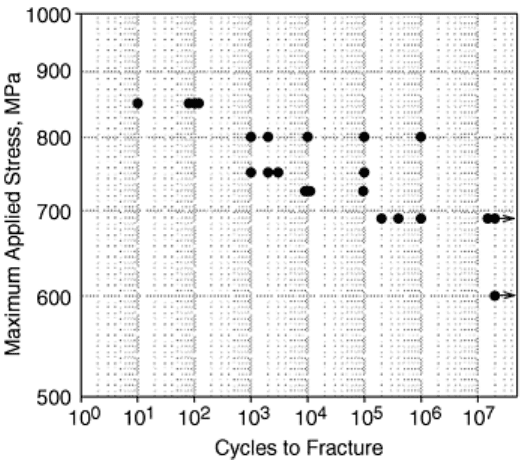
be halted after 10

cycles. An example of failure stress data as a function of the applied cycles is shown in Fig.

10.

Fig. 10 Example of the cycles to fracture for a ceramic material subjected to cyclic loading. Adapted

from Ref 16

Axial cyclic tensile fatigue testing can be performed with ASTM C 1361 “Standard Practice for Constant-

Amplitude, Axial Tension-Tension Cyclic Fatigue of Advanced Ceramics at Ambient Temperatures” (Ref 19).

Any of the tensile test specimens specified in ASTM C 1273 “Standard Test Method for Tensile Strength of

Monolithic Advanced Ceramics at Ambient Temperatures” (Ref 69) are allowed. These include a variety of

cylindrical button-head specimens, pin-loaded dog-bone specimens, and shoulder-loaded dog-bone specimens.

The standard allows any frequency, waveform, and R ratio as needed for a particular application. A test may be

terminated for any of four reasons: specimen fracture, reaching a predetermined number of run-out cycles,

reaching a predetermined specimen compliance or material elastic modulus, or reaching a predetermined phase

lag between control mode and response.

Tension-compression cyclic fatigue has been attained by use of the button-head tensile specimen and a

clamping and alignment fixture (Ref 39). Fully reversed bending fatigue can also be attained with flexure

specimens by use of two symmetric sets of load and support pins (Ref 70).

Another cyclic fatigue test method that has been applied to ceramics is rotary bending (Ref 71, 72). This

approach is particularly relevant to applications involving shafts, such as ceramic turbocharger rotors. The

method avoids problems associated with edge finish by using cylindrical specimens, and a wide range of

frequencies is easily attained. Tests run on alumina and silicon nitride at 57 Hz indicate a linear S-N curve to

cycles at which an indistinct knee occurs, implying a fatigue limit at ~10

cycles. The endurance stress

corresponded to about ¼ of the strength of the alumina and about ½ that of the silicon nitride. The fatigue

parameter n was 13 for the alumina and 25 for the silicon nitride, respectively, which is lower than those

typically determined for aluminas and silicon nitrides by static or dynamic techniques. The differences in the

fatigue parameters were attributed to the effect of reversed bending.

Cyclic fatigue of ceramics has also been performed by using cantilever bending of rectangular, dog-bone, and

tapered-beam test specimens at a variety of frequencies. Tapered beams and dog-bone specimens reduce the

probability that failure will occur at the support where the stress is a maximum. Figure 11 illustrates a tapered-

cantilever beam used to obtain 3000 Hz accelerated fatigue data on silicon nitride (Ref 39).

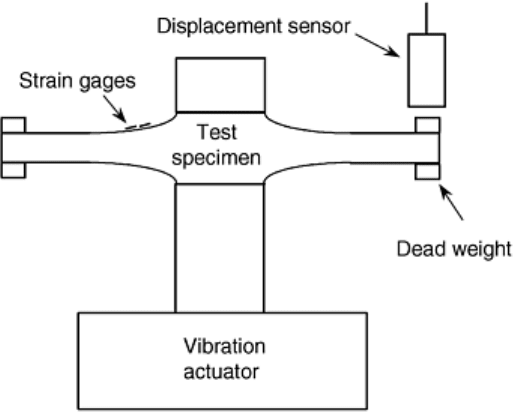
Fig. 11 Schematic of a high-frequency, tapered-cantilever beam test apparatus. Source: Ref 39

Testing of silicon nitride using tapered-cantilever beams at frequencies as high as 3000 Hz indicated a fatigue

limit at 40% of the monotonic strength (Ref 39). Interestingly, the life depended on the number of cycles rather

than the time and was well described by the modified Goodman diagram used to describe metallic fatigue. The

probability of failure was well described by the Weibull model. Axial tension-compression testing of the same

sintered silicon nitride indicated a fatigue limit around 10

cycles at a stress of 60% of the strength and an

increase in fatigue strength with increasing R ratio. The implication for this particular silicon nitride is that a

cyclic effect, rather than environmentally induced stress corrosion, dominated crack growth.

Tests using dog-bone specimens at 30 Hz (Ref 73) indicated no effect of cycling on the strength of two

different silicon nitrides for less than 10

cycles; however, relatively few specimens were tested. At

temperatures of 1200 and 1300 °C (2190 and 2370 °F), the effects of fatigue were more pronounced.

In contrast to the reversed fatigue results, tension-tension flexure fatigue of reaction-bonded, hot pressed, and

sintered silicon nitrides indicated environmentally related crack growth to be the failure-controlling mechanism

(Ref 74).

Fatigue testing of magnesia-partially-stabilized zirconia by using straight cantilever beams indicated a fatigue

limit around 10

cycles at a stress of 50% of the tensile strength (Ref 40). Reversed loading significantly

shortened the life of the material as compared with tension-tension loading.

Generally, servohydraulic actuators are used to generate cyclic fatigue loading of test specimens. However,

piezoelectric actuators in the form of stacks and cantilever spring plates also have been used (Ref 75, 76). These

systems allow relatively high frequencies (30 to 550 Hz) and compact test frames that do not require a

hydraulic pressure source. Figure 12 illustrates the test apparatuses.