ASM Metals HandBook Vol. 8 - Mechanical Testing and Evaluation
Подождите немного. Документ загружается.


Technology, Volume 18 of ASM Handbook.) Continuous rotation of one of the races can help prevent fretting
under these circumstances (Ref 11).
For convex washers and other convex contacts, a coating, nonmetallic shim, or lubricating film can help reduce
the surface shear forces.
References cited in this section
5. Proc. Specialists Meeting on Fretting in Aircraft Systems, AGARD-CP-161, Advisory Group for
Aerospace Research and Development, 1974
8. D.J. White, Proc. Inst. Mech. Eng., Vol 185, 1970–1971, p 709–716
9. C. Ruiz and K.C. Chen, Life Assessment of Dovetail Joints between Blades and Disks in Aero-Engines,
paper C241/86, Proc. Conf. Fatigue of Engineering Materials and Structures, Institute of Mechanical
Engineers, 1986, p 187–194
10. M. Takeuchi and R.B. Waterhouse, Fretting-Corrosion-Fatigue of High Strength Steel Roping Wire and
Some Protective Measures, Proc. Int. Conf. Evaluation of Materials Performance in Severe
Environments, EVALMAT 89, Iron and Steel Institute of Japan, 1989, p 453–460
11. J.A. Collins, Fretting, Fretting Fatigue, and Fretting Wear, Failure of Materials in Mechanical Design—
Analysis, Prediction, Prevention, 2nd ed., John Wiley & Sons, 1992, p 504–524
Fretting Fatigue Testing
S.J. Shaffer and W.A. Glaeser, Battelle Memorial Institute
Testing, Modeling, and Analysis
When fretting fatigue is encountered or anticipated, laboratory tests are usually required to find a solution. Test
results can also be used to develop an empirical model and are required for validation if a model is to be used
for design changes. This section presents types of fretting fatigue tests, the forms of results found in the
literature, and the effect of variables on fretting fatigue from different research test programs.
Types of Fretting Fatigue Tests. Fretting fatigue tests are designed to accomplish one of three goals. The first is
a test to predict or duplicate field failures and evaluate the effect of design changes or treatments based on
replication or simulation of service components and conditions. This is most useful if all the service conditions
are known and can be replicated or appropriately scaled, but the results will have limited applicability. A
second type of test uses a simple geometry and setup. The contact conditions may not be well defined or
directly applicable to a specific application, but they are assumed to be the same for every specimen set and
many tests can be conducted at a reasonable cost for screening new material combinations. In the third type of
fretting fatigue test, well-defined geometries and controlled and/or monitored loads and displacements are used.
These more fundamental tests are intended to evaluate the effect of specific variables such as amplitude,
clamping loads, reciprocating stresses, environments, or palliative methods, and to develop and validate fretting
fatigue models. In order to apply published test results to a specific component, the test parameters must be well
defined and understood for each engineering application. At present, work is under way to standardize test
methods in order to assist with this endeavor (Ref 2).
For most fretting fatigue testing, fretting pads are positioned on opposite faces of the sample and can be either
single or double footprints of flat or convex contact geometry. The relative displacement between the pads and
the sample can be driven independently or can be controlled by the loads and motion of the system (Fig. 10). Of
the four methods for cyclic loading of fretting fatigue specimens, general trends indicate that torsional
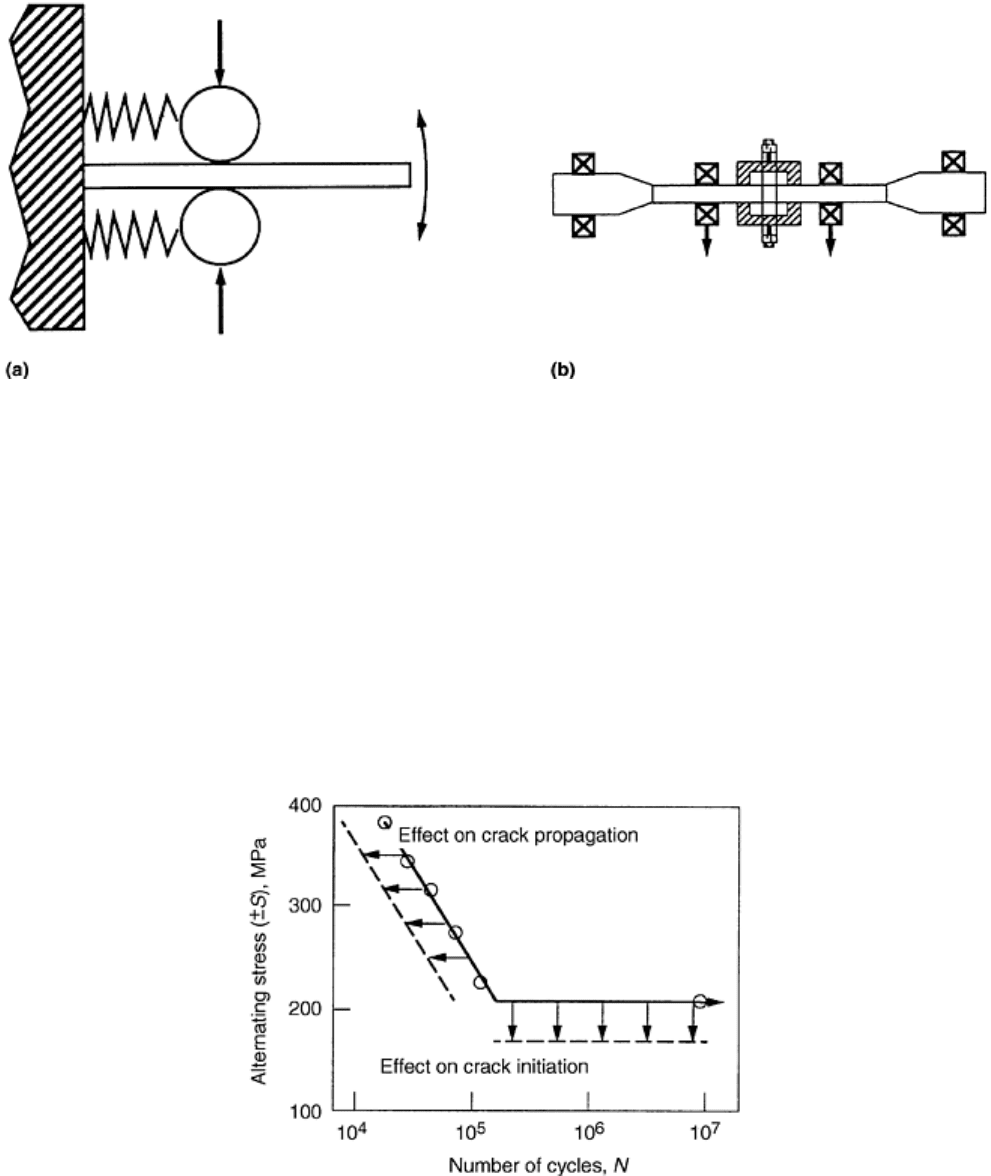
specimens have the smallest drop in fatigue strength, while the largest drop is for tests carried out under
rotating-bending or plane-reverse-bending conditions, with plane push-pull testing falling in between (Ref 7).
Fig. 10 Examples of fretting fatigue test configurations. (a) Cantilever beam reverse bending with single
pads. (b) Rotating fully reversing bending with double foot-pad bridges and proving ring
The influence of fretting on fatigue strength can be determined by two basic methods. In one method, a sample
is subjected to a certain number of cycles of fretting, followed by standard fatigue testing to failure without
fretting. Plots of fretting cycles versus total cycles are recorded. This method has been used to determine the
number of cycles for fatigue-crack detection under the given geometry, material, normal stress, applied
reversing stress, and relative slip amplitude (Ref 12).
Influence of Fretting on S-N Plot. In the second method, the sample is subjected to fretting for the entire test.
The fretting fatigue life or strength is determined by plotting the number of cycles to failure on an S-log N curve
where ±S is the alternating stress. The strength-reduction factor (SRF) is defined by the ratio of the plain fatigue
strength to the fretting fatigue strength as shown in Fig. 11 and is attributed to a decrease in crack nucleation
time. A shift in cycles to failure at a given strength level is attributed to an increase in crack propagation rate
and is often observed under corrosive environments.
Fig. 11 Effect of fretting on fatigue strength reduction through crack initiation. Fatigue strength
reduction is equal to the difference between the solid and dashed lines.
The number of cycles to failure can be defined either as full specimen rupture or by initiation of a propagating
(into the bulk stress region) crack. Crack length can be determined either from cross-sectional metallography or
by specimen compliance methods.
Stress Analysis, Modeling, and Prediction of Fretting Fatigue. Testing, stress analysis, and modeling are
complementary techniques required for understanding and predicting fretting fatigue behavior. For well-defined
conditions, test results provide input to models. These models aim to predict crack-initiation location, time,
propagation rate, and the effect of changes in variables on these factors. At present, prediction of fretting
fatigue is less developed than for plain (unnotched) fatigue. The main limitation is that continuum-mechanics
approaches do not consider microstructural inhomogeneities, and crack nucleation is controlled by such factors
as well as “short” fatigue-crack propagation.
Most of the early work in stress-field modeling for fretting fatigue uses, as a starting point, analysis similar to
that used by Mindlin (Ref 6) of a sphere pressed into a half plane and expands this to consider other geometries
and imposed shear loads. If stress fields are computed using FEM analysis, an assumed contact geometry and
coefficient of friction are used, and loads are imposed at various mesh locations in order to compute stresses
and subsequent strains. Alternatively, displacements can be imposed and strains and stresses computed. To
facilitate modeling, the stress singularity associated with an abrupt contact geometry change, such as at the edge
of a bolted flange or a hub/shaft interface, is accommodated by plastic deformation, and a limiting stress is
assumed. Current models are limited in that changes in contact geometry due to wear and variations in
coefficient of friction due to lubrication or debris accumulation are difficult to take into account.
Experiments have been undertaken and models have been proposed for both the full- and partial-slip regimes
and are based on empirical observations. Full-slip and partial-slip conditions can be achieved by varying the
test configurations.
In addition, while most fretting contacts are some combination of load- and displacement-controlled conditions,
laboratory experiments can be designed either to drive the fretting pads independently (displacement
controlled) or to allow them to move as a consequence of the clamping force and displacement of the “beam”
sample (load controlled).
For fretting under conditions of full slip, two early models predict the SRF due to fretting. Nishioka and
Hirakawa (Ref 13) derived the following equation to describe the fretting fatigue strength limit determined
using their displacement-controlled experiment setup with full-slip conditions under the fretting pads (Fig. 10).
σ
fw1
= σ
w1
- μp
o
{1 - e
(-d/K)
}
(Eq 2)
where σ
fw1
is the fretting fatigue strength, σ
w1
is the plain fatigue strength, p
o
is the clamping pressure, δ is the
slip amplitude (in mm), and K is a constant dependent on the material and surface condition (on the order of 3.4
× 10
-3
mm, or 1.34 × 10
-4
in., in Ref 13).
In later work of Wharton et al. (Ref 14), a similar form was developed in which notch sensitivity of the base
material was taken into account. The reduction in fatigue strength due to fretting was then proposed to also be
proportional to the shear stress resulting from the contact pressure of the cylindrical fretting pads, inversely
proportional to the contact width, and given by the equation:
σ
wf
= σ
wo
-q(8μP/πb)
(Eq 3)
where σ
wf
is the fatigue strength with fretting, σ
wo
is the fatigue strength without fretting, q is the notch
sensitivity factor, P is the load per unit length, and b is the contact width under the fretting pads (mm). Note
that both these predictions show that SRF is worse as μP or μP
o
is increased.
For probable location of fretting fatigue crack nucleation in the partial-slip regime, the approach of Ruiz and
Chen (Ref 9) can be used. In their analysis of a dovetail interface, a fretting parameter representing the energy
available for causing fretting damage, and given by the product of the slip amplitude, δ, and shear stress, τ, at
points under the interface, was computed. Next, the product στδ, called the fretting fatigue parameter, is
computed, where σ is the maximum surface tensile stress (resulting from the bulk cyclic loading). A fretting
fatigue crack is predicted to occur where the local value of στδ in the interface exceeds an empirically
determined critical value, or, fretting occurs when:
στδ ≥ στδ
crit
(Eq 4)
If στδ and στδ
crit
can be experimentally determined, then the designer can use this value as a design guide. Note
that both the slip amplitude and the shear stress depend on the coefficient of friction (with opposite responses)
and the imposed loading. Analysis by Nowell and Hills (Ref 15) of this work provided a theoretical justification
and a possible method for predicting “initiation” (or nucleation) time based on the total accumulated
incremental strain. With further effort, it appears that the composite parameter approach can be applied to
fretting fatigue in the full-slip regime and can be expanded to include plasticity.
Other models may be used to determine whether the conditions at the interface will be of full or partial slip and
to predict the location of the partial slip. These are generally FEM studies and make use of assumed
macroscopic contact conditions and bulk material properties. The text by Hills and Nowell covers this area; yet

it is claimed that no current models exist that can predict crack-initiation times strictly from the knowledge of
the states of stress, strain, and displacement on a macroscopic scale (Ref 16). Though experiments are required
to determine στδ
crit
, the most probable location of cracking may be predicted using FEM analysis and the
criteria of Ruiz and Chen (Ref 9). If conditions are sufficiently well defined, the slip characteristics of the
interfaces may also be predicted. Whether the interface is in full slip or the extent of partial slip will help guide
the choice of palliative. This article presents some palliatives that have been applied successfully in the past for
fretting abatement. However, the designer is advised to apply discretion in applying techniques listed because
results depend on the particular condition. In their review, Gordelier and Chivers (Ref 17) attribute
contradictory effects of similar treatments on fretting fatigue to the differing effects on the base materials and to
the different contact conditions.
References cited in this section
2. M.H. Attia and R.B. Waterhouse, Ed., Standardization of Fretting Fatigue Test Methods and
Equipment, STP 1159, ASTM, 1992
6. R.D. Mindlin, Compliance of Elastic Bodies in Contact, J. Appl. Mech., Vol 16, 1949, p 259–268
7. R.B. Waterhouse, Theories of Fretting Processes, Fretting Fatigue, Applied Science, 1981, p 203–220
9. C. Ruiz and K.C. Chen, Life Assessment of Dovetail Joints between Blades and Disks in Aero-Engines,
paper C241/86, Proc. Conf. Fatigue of Engineering Materials and Structures, Institute of Mechanical
Engineers, 1986, p 187–194
12. K. Nishioka and K. Hirakawa, Fundamental Investigations of Fretting Fatigue, Part 3, Some Phenomena
and Mechanisms of Surface Cracks, Bull. Jpn. Soc. Mech. Eng., Vol 12 (No. 51), 1969, p 397–407
13. K. Nishioka and K. Hirakawa, Fundamental Investigations of Fretting Fatigue, Part 5: The Effect of
Relative Slip Amplitude, Bull. Jpn. Soc. Mech. Eng., Vol 12 (No. 52), 1969, p 692–697
14. M.H. Wharton, R.B. Waterhouse, K. Hirakawa, and K. Nishioka, The Effect of Different Contact
Materials on the Fretting Fatigue Strength of an Aluminum Alloy, Wear, Vol 26, 1973, p 253–260
15. D. Nowell and D.A. Hills, Crack Initiation Criteria in Fretting Fatigue, Wear, Vol 136, 1990, p 329–343
16. D.A. Hills and D. Nowell, Mechanics of Fretting Fatigue, Kluwer Academic Publishers, 1994, p 210
17. S.C. Gordelier and T.C. Chivers, A Literature Review of the Palliatives for Fretting Fatigue, Wear, Vol
56, 1979, p 177–190
Fretting Fatigue Testing
S.J. Shaffer and W.A. Glaeser, Battelle Memorial Institute
Variables Investigated during Fretting Fatigue Tests
Of the dozens of variables that can potentially affect fretting (Ref 18), the three primary variables that control
fatigue-crack initiation are surface contact stress, slip amplitude, and coefficient of friction. All other variables
are secondary and affect fretting and fretting fatigue through their influence on the primary variables.
Unfortunately, many contradictory data appear in the literature (Ref 17). The contradictions concern whether
the fretting conditions were displacement controlled or load controlled and the interactions of the secondary
variables between each other and the primary variables. This section presents the results of various
investigations into the effect of variables on fretting fatigue.
Contact Stress and Alternating Stress. Contact stresses include both normal and shear stresses imposed at the
sample surface. The cyclic shear stresses at the surface are the cause of crack nucleation (where the propensity
to cracking from the stress state is also affected by pits, corrosion, and other forms of surface degradation). The
magnitude of shear stresses depend on the imposed forces and displacements, the coefficient of friction,
macroscopic stress concentrations, and local asperity geometries and distribution. Nishioka and Hirakawa (Ref
19) reported that fretting fatigue strength based on fatigue-crack initiation (or nucleation) was found to decrease
linearly with increasing normal force. For fretting fatigue strength based on fracture, they found a critical
contact pressure, above which no further degradation occurred. Although their experiments did not reach this
level, a sufficiently high normal force can sometimes result in the closure of cracks initiated by fretting through
the superposition of a compressive stress.
Alternating stress is the stress imposed on the bulk sample, characterized by an amplitude and a mean stress.
For fully reversing bending (which occurs on a rotating shaft), the mean stress is zero. Nishioka and Hirakawa
performed experiments in reverse bending on annealed and induction-hardened medium-carbon steel under
displacement-controlled conditions (full slip). They found that the mean stress did not affect the range of
alternating stress amplitude for fatigue-crack initiation due to fretting, but that it did affect crack propagation
(Ref 19).
Wharton et al. also found that the percentage of fatigue life reduction due to fretting, defined by crack
propagation to failure, was independent of applied alternating stress level for 70/30 brass and for a 0.7% carbon
steel (Ref 20). These experiments were performed in rotating bending using flat fretting pad contacts (Ref 21,
22). Ruiz and Chen found that peak contact stress was important at 600 °C (1112 °F), but at room temperature
the fretting parameter, τδ, dominated (Ref 9). This was attributed to the nature of the oxide and the influence of
the wear debris.
Displacement (Slip Amplitude) and Direction. For conditions of full slip, there is general agreement in the
literature that the effect is most severe for slip amplitudes of 20 to 25 μm (787–984 μin.). In work on 4130
steel, Gaul and Duquette (Ref 23) found that for clamping pressures of 20 to 41 MPa (3–6 ksi), a minimum in
the fatigue life at a given alternating stress occurred at a slip amplitude of 20 μm (787 μin.). At amplitudes
higher than this, the wear rate due to fretting exceeded the rate of crack growth rate just after initiation and the
fretting fatigue strength increased. A similar critical amplitude of relative slip, on the order of 15 to 20 μm
(590–787 μin.), was found by Nishioka and Hirakawa (Ref 13) for both induction-hardened and quenched-and-
tempered medium-carbon steel samples. Clamping pressures of 120 MPa (17 ksi) were used in their work. They
also concluded that the fatigue strength-reduction factor due to fretting can be minimized if the fretting
amplitude (relative slip) can be kept below 5 μm (197 μin.).
An effect related to slip amplitude is that of contact width. Experiments showed that larger-diameter cylinders
had a greater detrimental effect on fretting fatigue life for the same line contact stress than small-diameter
cylinders (Ref 24). This may be caused by increased partial slip or more asperity contacts per stress cycle.
Nowell and Hills (Ref 15) looked at the effect of slip amplitude through elastic modeling of fretting fatigue in
the partial-slip regime. In low-amplitude fretting experiments using cylindrical-radii fretting pads pressed
against an in-plane tension/compression loaded Al-4Cu alloy sample, they found a critical contact width for
fretting fatigue damage. They also found that a transition between long and short fatigue lives occurred for
microslip amplitudes of 0.9 to 1.2 μm (35–47 μin.) in the slip zones. This is considerably smaller than the
maximum damage displacement of 20 to 30 μm (787–1181 μin.) found by Nishioka and Hirakawa and others in
their full-slip experiments on steel samples.
The results of work by Collins and Tovey (Ref 25) indicate that fretting motion in the same direction as the
cyclic stress has a greater effect than fretting in the perpendicular direction. They used this result to conclude
that cracks are nucleated by adhesive wear rather than by abrasive plowing via the expected orientation from
each mode.
Coefficient of Friction. The coefficient of friction probably has the greatest influence on fretting fatigue. It
influences both slip amplitude and shear stress, though in opposite ways. The influence of different material
combinations on fretting fatigue life has been reported to be due to the coefficient of friction (Ref 14). For load-
controlled fretting, an increase in coefficient of friction can prevent slip over the whole contact region and
reduce or eliminate fretting fatigue. For amplitude-controlled fretting, the opposite effect can be expected, and a
reduction in the coefficient of friction is desired because the surface shear stresses are reduced. Reduction in the
coefficient of friction for clamped (bolted or riveted) joints has been shown to be detrimental in some cases
because the lower coefficient of friction between the overlapping plates increases the load-carrying
requirements of the bolts or rivets leading to failures initiating at the hole edges (Ref 17).
High Temperature. Fretting fatigue strength decreases with increasing temperature for titanium alloys (Ref 26),
but was found to increase for the nickel-base alloy Inconel 718 (Ref 27) due to the formation of a protective
oxide glaze. Such glazes typically lower the coefficient of friction. For iron-base alloys, both hard and soft
flame-sprayed coatings based on molybdenum have shown success in improving the fretting fatigue strength at
300 °C (572 °F). Overs et al. (Ref 28) attribute the improvement to MoO
2
glaze formation.
Environment and Corrosive Media. The effect of environment on fretting fatigue depends on the material and
its corrodibility. Fretting action readily destroys passivating films on materials that are normally corrosion
resistant. Poon and Hoeppner found that when fretting and corrosion occur simultaneously, the effect of
corrosion on fatigue is dominant (Ref 29). As such, many palliatives or remedies for fretting fatigue can be
viewed in terms of their effectiveness on corrosion fatigue.
In mildly corrosive aqueous environments, such as weak sodium-chloride solutions representative of human
body fluids, the fretting fatigue strength of materials not resistant to corrosion is reduced compared with fretting
fatigue in air. Corrosion-resistant materials, such as austenitic stainless steel and titanium, have reduced fretting
fatigue strengths in both environments due to the disruption by fretting of the otherwise protective oxide (Ref
30).
Endo found that ductile carbon steels are not affected by water vapor in fretting fatigue (Ref 31). Nishioka and
Hirakawa found corrosion to be a secondary factor in fretting fatigue in their work on medium-carbon steels by
comparing test data from argon and air experiments (Ref 32). Somewhat in contrast, Endo found that the
fretting fatigue strength of carbon steel was higher in argon than in air, explaining that while the crack initiation
rate is almost the same, the crack propagation rate is lower in argon (Ref 31).
Aluminum alloys are known to be very sensitive to water corrosion under dynamic conditions. Endo found that
both crack initiation and propagation are accelerated by traces of water vapor due to corrosive attack, but not by
oxygen. In the case of argon versus air experiments, the removal of oxygen was found to decrease the tangential
stress due to soft aluminum wear debris accumulating between the mating surfaces (Ref 31). The alumina
formed on aluminum would, if broken, be expected to be more abrasive and give rise to higher shear stresses
than soft metallic wear debris.
Compared with tests in air, Ti-6Al-4V alloy was found to be adversely affected by corrosive atmospheres of
humid argon and 1% NaCl at alternating stress levels above 120 MPa (17 ksi), but improved fatigue life was
observed below 90 MPa (13 ksi) (Ref 33). The nature of the corrosion product was proposed to play a major
role, in some cases forming a compacted layer that shielded the metal against crack initiation. Hoeppner reports
that steel does not exhibit such a strong dependence on corrosion product (Ref 34).
Corrosion or oxidation are not required in the fretting process. Metallic fretting debris will form with gold or
platinum contacts or other nonoxidizable materials (Ref 35).
Microstructure and Material. If the design requirements permit their use, annealed materials were found to be
less susceptible to fretting fatigue than materials in the work-hardened state (Ref 20). Similarly, cast structures
were less susceptible than forged structures (Ref 36). These results imply that if fatigue-crack nucleation takes
place through a wear mode involving exhaustion of work hardening, then prior-worked materials have a
significantly shorter nucleation period.
Reeves and Hoeppner (Ref 37) found that carbon steel in the martensitic condition is more resistant to fretting
fatigue than in the normalized (ferrite-plus-pearlite) steel due to the higher hardness and wear resistance of the
martensitic steel. Nishioka and Hirakawa also found the fatigue limit to be higher on induction-hardened versus
annealed steel (Ref 19). These results imply that more wear-resistant materials have better fretting fatigue
properties.
Copper-Base Alloys. Wharton et al. (Ref 20) found that 70/30 brass does not show a strength limit in either
plain fatigue or fretting fatigue. However, they found that the fretting fatigue strength at a given number of
cycles is reduced by a fixed proportion over the plain fatigue strength for two microstructural conditions,
independent of applied stress. The reduction was 61 and 74%, for annealed and work-hardened brass,
respectively.
Ferritic Alloys. Endo and Goto (Ref 38) found that fatigue cracks generally initiate in ferrite grains, and
propagate perpendicular to the sliding direction through a pearlitic region, irrespective of the orientation of the
pearlite plates. Their experiments were performed under reverse bending. They also reported that for two-stage
tests on a medium-carbon steel (ferrite-plus-pearlite microstructure), no further reduction in fatigue life
occurred if the fretting was continued for the entire test or was stopped after one-quarter of the total life. They
concluded that the saturation point in the curve representing fretting cycles versus total fatigue cycles
corresponds to the point at which cracks that were initiated during fretting had grown to a depth where they
propagated solely due to the macroscopic repeated stress (Ref 38).
Titanium Alloys. For three alpha + beta titanium microstructures, a fine or acicular microstructure was found to
be more resistant to damage, defined by the number of propagating cracks found after a given number of cycles
at a fixed stress, than a coarser-annealed structure (Ref 7). The finer alloy structure also had a lower SRF.
References cited in this section
7. R.B. Waterhouse, Theories of Fretting Processes, Fretting Fatigue, Applied Science, 1981, p 203–220
9. C. Ruiz and K.C. Chen, Life Assessment of Dovetail Joints between Blades and Disks in Aero-Engines,
paper C241/86, Proc. Conf. Fatigue of Engineering Materials and Structures, Institute of Mechanical
Engineers, 1986, p 187–194
13. K. Nishioka and K. Hirakawa, Fundamental Investigations of Fretting Fatigue, Part 5: The Effect of
Relative Slip Amplitude, Bull. Jpn. Soc. Mech. Eng., Vol 12 (No. 52), 1969, p 692–697
14. M.H. Wharton, R.B. Waterhouse, K. Hirakawa, and K. Nishioka, The Effect of Different Contact
Materials on the Fretting Fatigue Strength of an Aluminum Alloy, Wear, Vol 26, 1973, p 253–260
15. D. Nowell and D.A. Hills, Crack Initiation Criteria in Fretting Fatigue, Wear, Vol 136, 1990, p 329–343
17. S.C. Gordelier and T.C. Chivers, A Literature Review of the Palliatives for Fretting Fatigue, Wear, Vol
56, 1979, p 177–190
18. J.A. Collins and S.M. Marco, The Effect of Stress Direction during Fretting on Subsequent Fatigue Life,
Proc. ASTM, Vol 64, 1964, p 547–560
19. K. Nishioka and K. Hirakawa, Fundamental Investigations of Fretting Fatigue, Part 4: The Effect of
Mean Stress, Bull. Jpn. Soc. Mech. Eng., Vol 12 (No. 51), 1969, p 408–414
20. M.H. Wharton, D.E. Taylor, and R.B. Waterhouse, Metallurgical Factors in the Fretting Fatigue
Behaviour of 70/30 Brass and 0.7% Carbon Steel, Wear, Vol 23, 1973, p 251–260
21. R.B. Waterhouse and D.E. Taylor, The Initiation of Fatigue Cracks in a 0.7% Carbon Steel by Fretting,
Wear, Vol 17, 1971, p 139–147
22. R.B. Waterhouse and M. Allery, The Effect of Powders in Petrolatum on the Adhesion between Fretted
Surfaces, Trans. ASLE, Vol 9, 1966, p 179
23. D.J. Gaul and D.J. Duquette, The Effect of Fretting and Environment on Fatigue Crack Initiation and
Early Propagation in a Quenched and Tempered 4130 Steel, Metall. Trans. A, Vol 11, Sept 1980, p
1555–1561
24. R.B. Waterhouse, Fretting Fatigue, Int. Mater. Rev., Vol 37 (No. 2), 1992, p 77–97
25. J.A. Collins and F.M. Tovey, Fretting-Fatigue Mechanisms and the Effect of Motion on Fatigue
Strength, J. Mater., Vol 7 (No. 4), 1972, p 460–464

26. M.M. Hamdy and R.B. Waterhouse, The Fretting Fatigue Behavior of Ti-6Al-4V at Elevated
Temperatures, Wear, Vol 56, 1979, p 1–8
27. M.M. Hamdy and R.B. Waterhouse, The Fretting Fatigue Behavior of a Nickel-Based Alloy (Inconel
718) at Elevated Temperatures, Wear of Materials, American Society of Mechanical Engineers, 1979, p
351–355
28. M.P. Overs, S.J. Harris, and R.B. Waterhouse, in Wear of Materials, American Society of Mechanical
Engineers, 1979, p 379–387
29. C. Poon and D.W. Hoeppner, The Effect of Environment on the Mechanism of Fretting Fatigue, Wear,
Vol 52, 1979, p 175–191
30. R.B. Waterhouse, Fretting Fatigue in Aqueous Electrolytes, Fretting Fatigue, R.B. Waterhouse, Ed.,
Applied Science, 1981, p 159–177
31. K. Endo, Practical Observations of Initiation and Propagation of Fretting Fatigue Cracks, Fretting
Fatigue, R.B. Waterhouse, Ed., Applied Science, 1981, p 127–141
32. K. Nishioka and K. Hirakawa, Some Further Experiments on the Fatigue Strength of Medium Carbon
Steel, Proc. Mech. Behav. Mater., Vol 3, 1971, p 308–318
33. M.H. Wharton and R.B. Waterhouse, Environmental Effects in the Fretting Fatigue of Ti-6Al-4V, Wear,
Vol 62, 1980, p 287–297
34. D.W. Hoeppner, Environmental Effects in Fretting Fatigue, Fretting Fatigue, R.B. Waterhouse, Ed.,
Applied Science, 1981, p 143–158
35. D. Godfrey and J. Bailey, Early Stages of Fretting of Copper, Iron and Steels, Lub. Eng., Vol 10, 1954,
p 155–159
36. G. Sachs and P. Stefan, Chafing Fatigue Strength of Some Metals and Alloys, Trans. ASM, Vol 29,
1941, p 373–401
37. R.K. Reeves and D.W. Hoeppner, Microstructural and Environmental Effects on Fretting Fatigue, Wear,
Vol 47, 1978, p 221–229
38. K. Endo and H. Goto, Initiation and Propagation of Fretting Fatigue Cracks, Wear, Vol 38, 1976, p 311–
324
Fretting Fatigue Testing
S.J. Shaffer and W.A. Glaeser, Battelle Memorial Institute
Prevention or Improvement
Fretting can be minimized or eliminated in many cases by one or more of the methods outlined in Table 1.
Additional techniques in the design stages to diminish the effect of fretting on fatigue are discussed in more
detail in this article in terms of:
• Modification of the surface stress state by introduction of compressive stresses, reduction of surface
shear stresses, or elimination or reduction of relative motion
• Application of principles for wear and fracture toughness in selection of materials, coatings, and
lubricants
Surface Stress Modification
Design for Introduction of Residual Compressive Stress. The only treatment or remedy that has been shown to
be universally effective in improving fretting fatigue is the introduction of residual compressive stresses. The
compressive stress will reduce the driving force for both crack initiation and propagation. Residual compressive
stresses can be imparted through high and uniform clamping forces or interference fits, plastic deformation of
the surfaces, phase changes, and precipitation or diffusion/thermal treatments. If sufficiently deep,
superposition of the compressive stress can also decrease the tensile stress field on the propagating crack in the
base material.
Plastic deformation by means of shot peening, surface rolling, or ballizing the inside diameter of through-holes
has the secondary effect of work hardening of the surface. In some cases, this work hardening leads to higher
resistance to fretting wear. Waterhouse and Saunders (Ref 39) have attributed the increase in fretting fatigue
strength of austenitic stainless steels by shot peening to an increase in surface hardness to 400 HV, compared to
150 HV for the bulk material, resulting in an increase in the fretting fatigue strength to that of the plain fatigue
strength without fretting. In contrast, Leadbeater et al. (Ref 40) found that the improved fretting fatigue life in
an aluminum 2014A alloy by shot peening was most likely due only to residual compressive stresses. They
determined that while increasing surface roughness had a small beneficial effect, work hardening did not
influence fretting fatigue properties.
Cold-working methods are not effective in applications where temperatures during service, or those generated
locally due to fretting, would lead to annealing of the previously work-hardened surface.
Nitriding is a very effective palliative for steels. It introduces residual compressive stresses in the surface, and
local hardening through solid solution strengthening can decrease the areas of real contact of self-mated ferrous
material couples. Both chemical and ion implantation nitriding methods can be used. The effectiveness of
carburizing will vary. Although the strength and hardness of the surface will be increased, the heat treatment
required to create the martensitic transformation, carburizing, can produce either compressive or tensile residual
stresses depending on the section size and shape. Tensile stresses, of course, would be detrimental.
Avoidance of Stress Raisers. Reducing geometric stress raisers in the vicinity of the contact will help prevent
fretting fatigue-crack nucleation. Examples were presented in the section “Parallel Surfaces without External
Loading” and in Fig. 7 and 8. Local stress raisers due to pitting by wear or pits caused by corrosion can be
prevented by corrosion-resistant coatings, such as zinc, or by cathodic protection.
Spacers or Shims. If the amplitude of relative displacement is small, it may be possible to absorb all of the
transmitted shear stresses through the elasticity of a thin, flexible layer such as rubber. The effectiveness of this
method depends on the modulus of the layer, its thickness, the severity of the normal load, and whether the
relative motion is displacement controlled. For aluminum alloys used for aircraft skins at temperatures up to
150 °C (302 °F), Taylor reports in work by Harris (Ref 41) that several investigations have shown the success
against fretting fatigue of a joint bonded with isocyanate epoxy resin loaded with MoS
2
. It is likely that the
solid lubricant lowered the transmitted shear stresses while the resin prevented metal-to-metal contact. It has
also been reported that both pure aluminum and copper are effective shim materials to be used against steel for
reducing the transmitted shear stresses (Ref 24).
Lubricants. By using lubricants to lower the coefficient of friction, shear stresses resulting from the normal load
will be decreased. Again, the amplitude of displacement may be increased. Oils and greases tend to be forced
from the interface. Rough surfaces, such as those left by a shot-peening operation, can help retain liquid
lubricants. Surface finishes that deliver oil to the fretting site are beneficial. Liquid lubricants can be effective
on wire rope, where there is some containment of the lubricant due to the outer strands. Solid lubricants tend to
be worn away over time and therefore have limited effectiveness.
Relative Motion. If the relative motion of the two members can be eliminated, the fatigue life can then be
computed using standard methods found elsewhere in this Volume. The design concern then shifts to
minimizing the stress concentration at the edges of the contact. Methods for eliminating motion include
increasing the normal load and/or increasing the coefficient of friction of the interface to expand the region of
no slip to the entire contact.
Surface Roughness. Surprisingly, a deliberately rough surface finish may be the best for minimizing fretting
fatigue damage. Waterhouse suggests machining grooves in the surface of one of the two contacting members,
preferably the one that is not subjected to the major cyclic stresses (Ref 42). It was suggested that the benefit
found in this work on aluminum was due to a minimization of the extent of any one contact area. An alternative
explanation is that the debris generated during fretting may be more readily trapped in the grooves, thus
promoting both a lubricating effect and a reduction in the local stresses due to support by the compacted debris.
Wear and Cracking Resistance
Material Selection for Fretting Fatigue Resistance. Two guides for materials selection choices should be used.
The first is based on materials and treatments selected for avoidance of fretting damage, hence minimizing
crack nucleation (see Table 2). Materials with low propensity for adhesion are described by Rabinowicz (Ref
44) in terms of the inverse of metallurgical compatibility. Typically, dissimilar couples are preferred. Self-
lubricating components, such as porous metal washers impregnated with lubricant, can be used. Materials with
high work-hardening capacity or dynamic recrystallization characteristics can also minimize fatigue-crack
initiation.
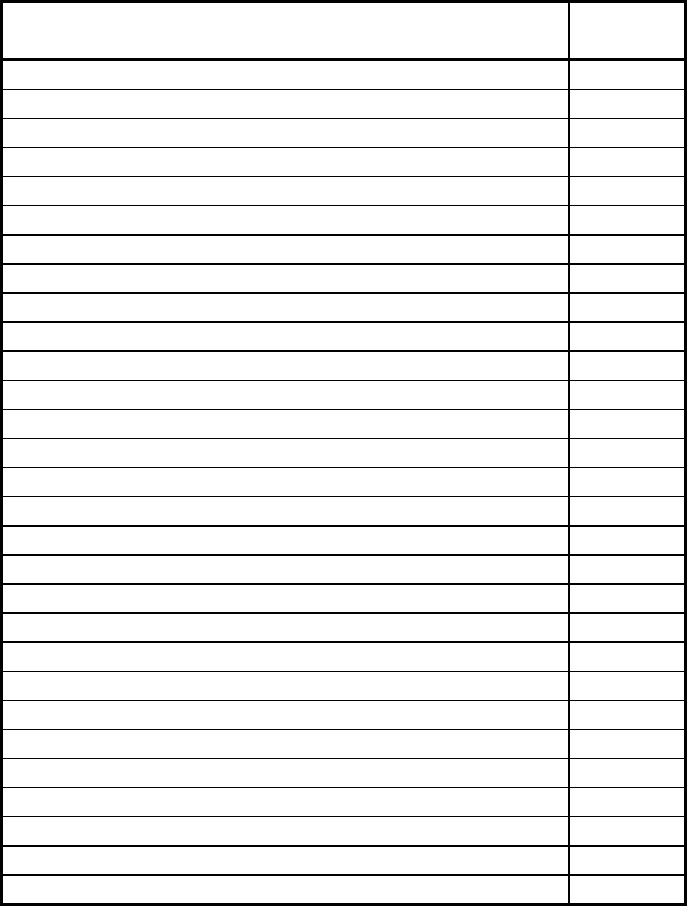
Table 2 Relative fretting resistance of various material combinations
Combination
Fretting
resistance
Aluminum on cast iron
Poor
Aluminum on stainless steel
Poor
Bakelite on cast iron
Poor
Cast iron on cast iron, with shellac coating
Poor
Cast iron on chromium plating
Poor
Cast iron on tin plating
Poor
Chromium plating on chromium plating
Poor
Hard tool steel on stainless steel
Poor
Laminated plastic on cast iron
Poor
Magnesium on cast iron
Poor
Brass on cast iron
Average
Cast iron on amalgamated copper plate
Average
Cast iron on cast iron
Average
Cast iron on cast iron, rough surface
Average
Cast iron on copper plating
Average
Cast iron on silver plating
Average
Copper on cast iron
Average
Magnesium on copper plating
Average
Zinc on cast iron
Average
Zirconium on zirconium
Average
Cast iron on cast iron with coating of rubber cement
Good
Cast iron on cast iron with Molykote lubricant
Good
Cast iron on cast iron with phosphate conversion coating
Good
Cast iron on cast iron with rubber gasket
Good
Cast iron on cast iron with tungsten sulfide coating
Good
Cast iron on stainless steel with Molykote lubricant
Good
Cold-rolled steel on cold-rolled steel
Good
Hard tool steel on tool steel
Good
Laminated plastic on gold plating Good
Source: Ref 43
