ASM Metals HandBook Vol. 8 - Mechanical Testing and Evaluation

Подождите немного. Документ загружается.

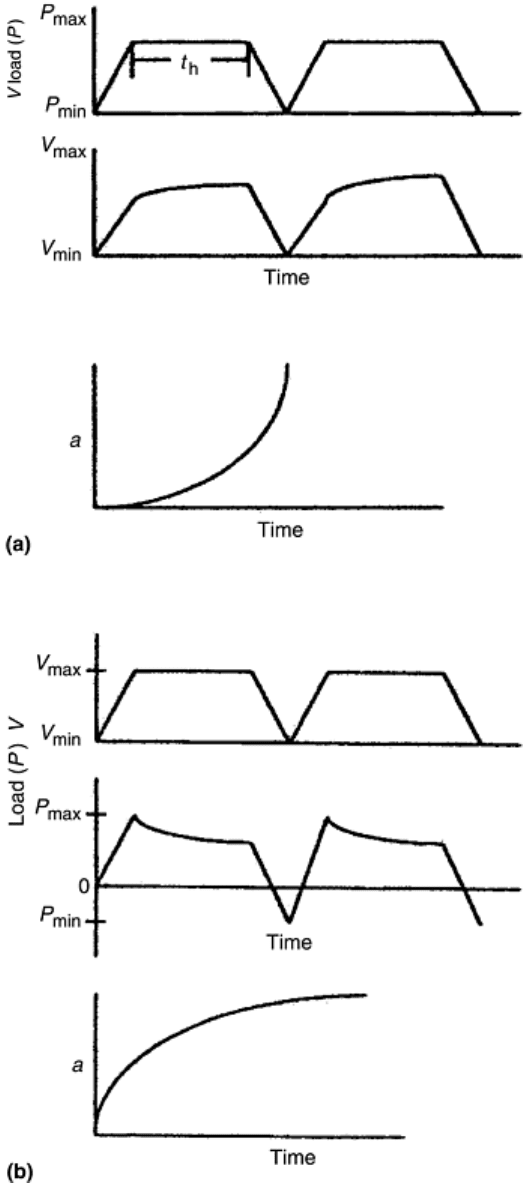
Fig. 4 Schematic comparison of (a) load-controlled and (b) displacement-controlled testing under

trapezoidal loading. Source: Ref 5

Due to matters of convenience, tests are most frequently conducted under load-controlled conditions. However,

there are a few advantages of displacement-controlled testing that should be considered. For instance, due to a

continuous rise in the net section stress ahead of the crack in load-controlled tests during crack growth, K

continually increases as the size of the remaining ligament decreases. Consequently, this means that the scale of

creep in the specimen increases as the test progresses, which causes ratcheting in the specimen as the inelastic

deflection accumulates with the completion of each cycle (Ref 5). Comparatively, as can be seen in Fig. 4(b),

the applied load decreases with crack extension in displacement-controlled tests, so ratcheting is avoided (Ref

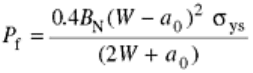
44). Also, data can be collected for greater crack extensions in displacement-controlled tests than in load-

controlled tests. Overall, load-controlled tests are more suitable for low crack growth rates, and displacement-

controlled tests are suited for higher crack growth rates (greater than 4 × 10

-6

mm/cycle) and tests with

extensive hold times (Ref 5).

Grips and Fixtures. For the CT specimen, a pin and clevis assembly should be used at both the top and bottom

of the specimen. This assembly will allow in-plane rotation as the specimen is loaded. Materials for the grips

and pull rods should be creep resistant and able to withstand the temperature environment to which they will be

exposed during the test. Examples of current elevated-temperature materials being used include AISI grade 304

and 316 stainless steels, grade A 286 steel, Inconel 718, and Inconel X750. The loading pins should be

machined from temperature-resistant steels, such as A 286, and should be heat treated to ensure that they

acquire a high resistance to creep deformation and rupture.

Heating Devices. Samples are generally heated by means of either an electric resistance furnace or a laboratory

convection oven. Before the application of load and for the duration of the test, the difference between the

temperature indicated by the device and the nominal test temperature is not to exceed ±2 °C (±3 °F) for

temperatures at or below 1000 °C (1800 °F). It is to remain within ±3 °C (±5 °F) for temperatures above 1000

°C (1800 °F). In the initial heating of the specimen, it is important to avoid temperature overshoots that could

potentially affect test results. In order to measure the specimen temperature, a thermocouple must be attached to

the specimen. The thermocouple should be placed in the uncracked ligament region of the sample 2 to 5 mm

(0.08–0.2 in.) above or below the crack plane. If the width of the specimen exceeds 50 mm (2 in.), it is

advisable to attach multiple thermocouples at evenly spaced intervals in the uncracked ligament region around

the crack plane, as stated previously. Thermocouples must be kept in intimate contact with the specimen. In

order to avoid short circuiting, ceramic insulators should cover the individual wires of the temperature circuit.

Fatigue Precracking. In order to eliminate the effects of the machined notch and to provide a sharp crack tip for

crack initiation, it is necessary to precrack creep and/or creep-fatigue test specimens. An extensively detailed

method for the process can be found in ASTM E 399, “Test Method for Plane-Strain Fracture Toughness of

Metallic Materials” (Ref 45). Specimen precracking must be conducted in the same condition as it is going to

be tested. The temperature is to be at or above room temperature and must not exceed the designed test

temperature. For the process of precracking, equipment must be used that is capable of applying a symmetric

load with respect to the machined notch and must be able to control the maximum stress intensity factor, K

max

to within ±5%. The fatigue load used during the process must remain below the following maximum value (Ref

23):

(Eq 42)

where B

is the corrected specimen thickness, W is the specimen width, a

is the initial crack length measured

from the load line, and σ

is the yield strength. While the fatigue precrack is in the final 0.64 mm (0.025 in.) of

extension, the maximum load shall not exceed P

or a load such that the ratio of the stress intensity factor range

to Young's modulus (ΔK/E) is equal to or less than 0.0025 mm 1/2 (0.0005 in. 1/2), whichever is less (Ref 23).

In this manner, it is ensured that the final precrack loading will not exceed that of the initial creep or creep-

fatigue crack growth test.

The crack length for the fatigue precrack can be measured using the same methods described in the next

section, “Test Procedure,” for monitoring crack length during crack growth testing. Measurements of the

fatigue precrack must be accurate to within 0.1 mm (0.004 in.). Measurements must be taken on both surfaces,

and their values must not differ by more than 1.25 mm (0.05 in.). If surface cracks are allowed to exceed this

limit, further extension will be required until the aforementioned criteria are met (Ref 5). The total initial crack

length (the starter notch plus fatigue precrack) must be at least 0.45 times the width, but no longer than 0.55

times the width.

References cited in this section

5. R.H. Norris, P.S. Grover, B.C. Hamilton, and A. Saxena, Elevated Temperature Crack Growth, Fatigue

and Fracture, Vol 19, ASM Handbook, ASM International, 1996

22. P.K. Liaw, A. Saxena, and J. Schaefer, Estimating Remaining Life of Elevated Temperature Steam

Pipes, Part I: Material Properties, Eng. Fract. Mech., Vol 32, 1989, p 675

23. “Standard Test Method for Measurement of Creep Crack Growth Rates in Metals,” ASTM E 1457,

American Society for Testing and Materials, 1998

42. A. Saxena, Limits of Linear Elastic Fracture Mechanics in the Characterization of High-Temperature

Fatigue Crack Growth, Basic Questions in Fatigue, Vol 2, STP 924, R. Wei and R. Gangloff, Ed.,

ASTM, 1989, p 27–40

43. “Practices of Load Verification of Testing Machines,” E 4 94, Annual Book of Standards, Vol 3.01,

ASTM, 1994

44. A. Saxena, R.S. Williams, and T.T. Shih, Fracture Mechanics—13, STP 743, ASTM, 1981, p 86

45. “Test Method for Plane-Strain Fracture Toughness of Metallic Materials,” E 399, Annual Book of ASTM

Standards, Vol 3.01, ASTM, 1994, p 680–714

Creep Crack Growth Testing

B.E. Gore, Northwestern University, W. Ren, Air Force Materials Laboratory, P.K. Liaw, The University of Tennessee

Test Procedure

Number of Tests. Data collected during creep crack growth rate testing will inherently exhibit scatter. Values of

da/dt at a given value of C*(t) can vary by as much as a factor of two (Ref 23, 46). This inherent scatter can be

further augmented by variables, such as microstructural differences, load precision, environmental control, and

data processing techniques (Ref 23). It is thus advised that replicate tests be conducted; when this is

impractical, multiple specimens must be tested in order to obtain regions of overlapping da/dt versus C*(t) data.

Assurance of the inferences drawn from the data is augmented by increasing the number of tests conducted.

Test Setup. Prior to testing, it is necessary to take measures to prepare for the measurements of the crack length,

load-line displacement, temperature, and number of completed cycles. As discussed in subsequent sections, the

electric potential drop method, in which fluctuations in potential in a constructed voltage loop are monitored, is

often used to calculate the crack length during testing. In order to prepare for this method, the specimen must be

fitted with current input and voltage leads to the current source and potentiometer, respectively. The fitting can

be conducted either prior to or just after specimen installation according to preference. In order to avoid contact

with other components in the test setup that could potentially skew results, the leads can be covered with

protective ceramic insulators. In order to begin installation of the specimen, both clevis pins must be inserted,

after which a small load of approximately 10% of the intended test load should be applied in order to bolster the

axial stability of the load train. At this point, the extensometer must be placed along the load line of the

specimen in order to monitor load-line displacements. Care must be taken to make sure that the device is in

secure contact with the knife edges. Subsequently, the thermocouples must be attached to the specimen by

being placed in contact with the crack plane in the uncracked ligament region. Lastly, the furnace must be

brought into position, and heating of the specimen should begin. The initialization of the current for the electric

potential system must be in concordance with the point of turning on the furnace. This is because resistance

heating of the specimen will occur as a result of the applied current.

In order to avoid overshoots in temperature exceeding the limits set forth previously, it is recommended that the

heating of the specimen be slow and steady. It may even be desirable to stabilize the temperature at an

increment of 5 to 30 °C (10–50 °F) below the final testing temperature and then make adjustments as necessary.

Once the appropriate test temperature is achieved and stabilized, it should be held for a given amount of time

necessary to ensure that the temperature will be able to be maintained within the aforementioned limits. This

time is to be, at minimum, 1 hour per 25 mm (1 in.) of specimen thickness. After these requirements have been

met, a set of measurements must be recorded while in the initial no-load state for reference. It follows that the

next step is the application of the load. The load must be applied carefully in order that shock loads or inertial

loads can be avoided, and the length of time for the application of the load should remain as short as possible.

The load or K-level chosen depends on the required crack growth rates during the test. For effective testing, the

crack growth rates must be selected to mimic those encountered during the service life of a material. Without

delay, upon the completion of loading the sample, another set of measurements of electric potentials and

displacements must be taken to be used as the initial loading condition (time = 0).

Data Acquisition during Testing. The electric potential voltage, load, load-line displacement, test temperature,

and number of cycles must be monitored and recorded continuously throughout the test if autographic strip

chart recorders or voltmeters are used. If digital data acquisition systems are employed, a full set of readings

must be taken no less frequently than once every fifteen minutes. The resolution of these data acquisition

systems must be at least one order of magnitude better than the measuring instrument (Ref 5).

Crack Length Measurement. When monitoring creep crack propagation, the chosen technique should be able to

resolve crack extensions of at least 0.1 mm (0.004 in.). Surface crack length measurements by optical means,

such as a travelling microscope, are not considered reliable as a primary method due to the fact that crack

extension across the thickness of the specimen is not always uniform. However, optical observation may be

used as an auxiliary measurement method. For the aforementioned reason, the selected crack length

measurement technique must be capable of measuring the average crack length across the specimen thickness.

The most commonly used method for the determination of crack length in creep-fatigue crack growth testing is

the electric potential drop method. This method involves applying a fixed electric current and monitoring any

changes in the output voltage across the output locations. Because any increase in crack length (corresponding

to a decrease in the uncracked ligament) would result in an increase in the electric resistance, the final result is

an increase in the output voltage (Ref 5). The electric potential drop method is considered to be the most

compatible with elevated-temperature creep crack growth testing.

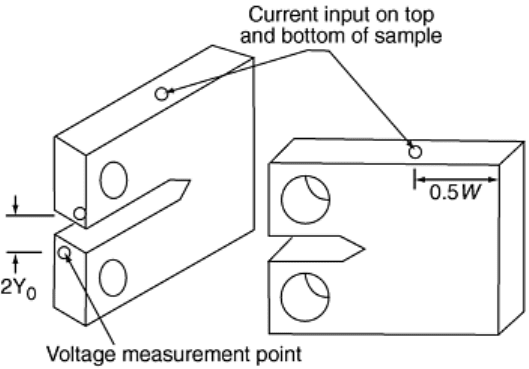
The input current and voltage lead locations for a typical CT specimen are shown in Fig. 5. The leads may be

attached either by welding them to the material or by connecting them to the material with screws. The choice

of the method essentially depends on the material and test conditions. For a soft material tested at relatively low

temperatures, threaded connections are fine, but for harder materials, it is recommended that the leads be

welded, especially for tests conducted at elevated temperatures (Ref 5). The leads must be long enough to allow

current input devices and output voltage measuring instruments to be far enough away from the furnace so as to

avoid excessive heating. In addition, leads should be about the same length to minimize lead resistance, which

contributes to the thermal voltage, V

, as described below. Concerning material choice for the leads, 2 mm

(0.08 in.) diameter stainless steel wires have been shown to work very well due to excellent oxidation resistance

at elevated temperatures. Nonetheless, any material that is resistant to oxidation and is capable of carrying a

current that is stable at the test temperature should be suitable. In the past, nickel and copper wires have been

effectively used as a lead material for tests conducted at lower temperatures (Ref 5).

Fig. 5 Input current and voltage lead locations for which Eq 43 applies. Source: Ref 22

In order to calculate the crack size for the setup shown in Fig. 5 from the measured output voltage and initial

voltage values, V and V

, the following closed-form equation should be used (Ref 47, 48):

(Eq 43)

where a

is the instantaneous crack length, W is the specimen width, Y

is the half distance between the output

voltage leads, V is the instantaneous output voltage, and a

is the reference crack size with respect to the

reference voltage, V

. Usually a

is the initial crack size after precracking, and V

is the initial voltage. Often the

voltages, V and V

, used for determining the crack size in the equation differ from their respective indicated

readings when using a direct current technique. This is due to V

, which can be caused by many factors,

including differences in the junction properties of the connectors, differences in the resistance of the output

leads, varying output lead lengths, and temperature fluctuations in output leads themselves (Ref 5). Measured

values of V

should be recorded before the load application and periodically throughout testing. To make these

measurements, the current source must be turned off; then the output voltage should be recorded. Before

calculations are made, the V

value must be subtracted from the respective V and V

so that the actual crack

extension length can be established.

When testing materials that have high electrical conductivity, fluctuations in V

are often seen. This type of

fluctuation can be of the same magnitude as the fluctuation in voltage that accompanies crack growth and

could, therefore, veil this information. Because of this potential variation, it is recommended that the direct

current electric potential drop method not be the only nonvisual method for crack length measurements chosen.

Other more sophisticated techniques, such as the reversing current potential method, are recommended for use.

The reversing direct current electrical potential drop (RDCEPD) method is simply a variation of the electrical

potential drop method described by Johnson (Ref 47). This method is more sensitive to crack growth near the

specimen surface. In the RDCEPD method, a direct current is used, but the polarity is reversed at a fairly low

frequency (Ref 49). This step compensates for zero drift errors. Refer to Caitlin, et al. (Ref 50) for a more

detailed description of this crack length monitoring method.

It is imperative to keep in mind, while performing creep crack propagation tests, the importance of maintaining

a nearly straight crack front. The initial and final crack lengths must fluctuate no more than 5% across the

specimen thickness. Often the maintenance of a straight crack front depends on the material and the sample

thickness. It has been noted before that thicker specimens sometimes experience crack tunneling, or nonstraight

crack extension. Crack tunneling (thumbnail-shaped crack fronts) is common in specimen configurations that

are not side grooved (parallel-sided) (Ref 5, 7). Side-grooving the specimens can minimize the occurrence of

crack tunneling. Side grooves of 20% reduction have been found to work well in several materials, although

reductions of up to 25% are considered to be acceptable. The included angle of the grooves is usually less than

90° with a root radius less than or equal to 0.4 ± 0.2 mm (0.016 ± 0.008 in.). It is important to perform the

precracking of the specimen before the side grooving, as it is difficult to detect the precrack when located in the

grooves.

Load-Line Displacement Measurements. Load-line displacements can be described as those that occur at the

loading pins due to the crack associated with the accumulation of creep strains. In order to be able to ultimately

determine the crack-tip parameters, it is necessary to continually record the displacement measurements. These

displacement measurements must be taken as close to the load line as possible. The measuring device must be

attached on the knife edges of a CT specimen. Alternatively, for CCT specimens, the displacement should be

measured on the load line at points ±35 mm (±1.40 in.) from the crack centerline (Ref 5). In order to directly

measure the displacement, an elevated-temperature clip gage may be attached to the specimen (strain gages for

up to approximately 150 °C, or 300 °F, or capacitance gages for higher temperatures), and then the entire

assembly should be placed in the furnace. Instead, if the devices mentioned previously are not available, the

displacements can be transferred outside the furnace using a rod and tube assembly. In this case, the

transducer—a direct current displacement transducer (DCDT), linear variable displacement transducer (LVDT),

or capacitance gage—is placed outside the furnace. It is important that the rod and tube be made of materials

that are thermally stable and be fabricated of the same material to avoid any adverse effects caused by

differences in thermal expansion coefficients (Ref 23). The deflection measurement devices should have a

resolution of at least 0.01 mm (0.0004 in.) (Ref 5).

Post-Test Measurements. When the test has been completed, whether due to specimen failure or to the

acquisition of sufficient crack growth data, the load should be removed, and the furnace be turned off. Once the

specimen has cooled down adequately, it should be removed from the machine. The initial crack length (due to

precracking) and the final crack length (resulting from creep crack growth) should be measured at nine points

equidistant from each other along the face of the crack. The collected data can be processed using a computer

program that uses either the secant method or the seven-point polynomial method to calculate the deflection

rates, dV/dt, crack growth rates, da/dt, and the crack-tip parameters. For a more detailed description of these

methods refer to ASTM E 1457 (Ref 23).

References cited in this section

5. R.H. Norris, P.S. Grover, B.C. Hamilton, and A. Saxena, Elevated Temperature Crack Growth, Fatigue

and Fracture, Vol 19, ASM Handbook, ASM International, 1996

7. A. Saxena, “Recent Advances in Elevated Temperature Crack Growth and Models for Life Prediction,”

Advances in Fracture Research: Proc. Seventh Int. Conf. on Fracture, March 1989 (Houston, TX), K.

Salama, K. Ravi-Chander, D.M.R. Taplin, and P. Rama Rao, Ed., Pergamon Press, 1989, p 1675–1688

22. P.K. Liaw, A. Saxena, and J. Schaefer, Estimating Remaining Life of Elevated Temperature Steam

Pipes, Part I: Material Properties, Eng. Fract. Mech., Vol 32, 1989, p 675

23. “Standard Test Method for Measurement of Creep Crack Growth Rates in Metals,” ASTM E 1457,

American Society for Testing and Materials, 1998

46. A. Saxena and J. Han, “Evaluation of Crack Tip Parameters for Characterizing Crack Growth Behavior

in Creeping Materials,” ASTM Task Group E24-04-08/E24.08.07, American Society for Testing and

Materials, 1986

47. H.H. Johnson, Mater. Res. Stand., Vol 5 (No. 9), 1965, p 442–445

48. K.H. Schwalbe and D.J. Hellman, Test Evaluation, Vol 9 (No. 3), 1981, p 218–221

49. P.F. Browning, “Time Dependent Crack Tip Phenomena in Gas Turbine Disk Alloys,” doctoral thesis,

Rensselaer Polytechnic Institute, Troy, NY, 1998

50. W.R. Caitlin, D.C. Lord, T.A. Prater, and L.F. Coffin, The Reversing D-C Electrical Potential Method,

Automated Test Methods for Fracture and Fatigue Crack Growth, STP 877, W.H. Cullen, R.W.

Landgraf, L.R. Kaisand, and J.H. Underwood, Ed., ASTM, 1985, p 67–85

Creep Crack Growth Testing

B.E. Gore, Northwestern University, W. Ren, Air Force Materials Laboratory, P.K. Liaw, The University of Tennessee

Life-Prediction Methodology

In recent years, the subject of remaining-life prediction has drawn considerable attention. The interest in the

issue of remaining-life prediction stems from the necessity to avoid costly forced outages, from the need to

extend the component life beyond the original design life for economic reasons, and from safety considerations

(Ref 7, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, and 62). A closer look at the method of predicting the life

of materials can be found in Ref 61. Here, high-temperature structural components in power plants are

analyzed. Steam pipes, for example, are generally subject to elevated-temperature operating conditions.

Because of the high-temperature exposure and the simultaneous internal-pressure loading, the pipes are prone

to creep damage. Thus, material properties including creep data of in-service or ex-service steels are critical

input parameters for accurate life assessment of steam-pipe systems.

Figure 1, again, shows a schematic of the general remaining-life-prediction methodology for high-temperature

components (Ref 52). The life-prediction methodology can be separated into three steps. In step 1, two kinds of

pertinent material testing are performed (i.e., creep crack growth and creep deformation and rupture

experiments). By combining the results of these two tests and tensile tests, the rates of creep crack propagation,

da/dt, can be characterized by the creep crack growth rate correlating parameter (C

) (Ref 9, 31, 51, 52, and 63).

In step 2, the value of C

for a structural component containing a defect is calculated and used to estimate the

creep crack growth rate. In step 3, the creep crack propagation rate equation—da/dt versus C

—and the

calculated value of C

for the structural component are combined to develop residual life curves, such as a plot

of initial crack size versus remaining life. The final life of the structural component can be determined based on

certain failure criteria (e.g., fracture toughness).

References cited in this section

7. A. Saxena, “Recent Advances in Elevated Temperature Crack Growth and Models for Life Prediction,”

Advances in Fracture Research: Proc. Seventh Int. Conf. on Fracture, March 1989 (Houston, TX), K.

Salama, K. Ravi-Chander, D.M.R. Taplin, and P. Rama Rao, Ed., Pergamon Press, 1989, p 1675–1688

9. P.K. Liaw, A. Saxena, and J. Schaefer, Predicting the Life of High-Temperature Structural Components

in Power Plants, JOM, Feb 1992

31. A. Saxena, Creep Crack Growth Under Nonsteady-State Conditions, ASTM STP 905, Seventeenth

ASTM National Symposium on Fracture Mechanics, American Society for Testing and Materials, 1986,

p 185–201

50. W.R. Caitlin, D.C. Lord, T.A. Prater, and L.F. Coffin, The Reversing D-C Electrical Potential Method,

Automated Test Methods for Fracture and Fatigue Crack Growth, STP 877, W.H. Cullen, R.W.

Landgraf, L.R. Kaisand, and J.H. Underwood, Ed., ASTM, 1985, p 67–85

51. P.K. Liaw, A. Saxena, and J. Schaefer, Eng. Fract. Mech., Vol 32, 1989, p 675, 709

52. P.K. Liaw and A. Saxena, “Remaining-Life Estimation of Boiler Pressure Parts—Crack Growth

Studies,” Electric Power Research Institute, EPRI CS-4688, Project 2253-7, final report, July 1986

53. P.K. Liaw, M.G. Burke, A. Saxena, and J.D. Landes, Met. Trans. A, Vol 22, 1991, p 455

54. P.K. Liaw, G.V. Rao, and M.G. Burke, Mater. Sci. Eng. A, Vol 131, 1991, p 187

55. P.K. Liaw, M.G. Burke, A. Saxena, and J.D. Landes, Fracture Toughness Behavior in Ex-Service Cr-

Mo Steels, 22nd ASTM National Symposium on Fracture Mechanics, STP 1131, ASTM, 1992, p 762–

789

56. P.K. Liaw and A. Saxena, “Crack Propagation Behavior under Creep Conditions,” Int. J. Fract., Vol 54,

1992, p 329–343

57. W.A. Logsdon, P.K. Liaw, A. Saxena, and V.E. Hulina, Eng. Fract. Mech., Vol 25, 1986, p 259

58. A. Saxena, P.K. Liaw, W.A. Logsdon, and V.E. Hulina, Eng. Fract. Mech., Vol 25, 1986, p 289

59. V.P. Swaminathan, N.S. Cheruvu, A. Saxerna, and P.K. Liaw, “An Initiation and Propagation Approach

for the Life Assessment of an HP-IP Rotor,” paper presented at the EPRI Conference on Life Extension

and Assessment of Fossil Plants, 2–4 June 1986 (Washington, D.C.)

60. N.S. Cheruvu, Met. Trans. A, Vol 20, 1989, p 87

61. R. Viswanathan, Damage Mechanisms and Life Assessment of High-Temperature Components, ASM

International, 1989

62. C.E. Jaske, Chem. Eng. Prog., April 1987, p 37

63. P.K. Liaw, A. Saxena, and J. Schaefer, Creep Crack Growth Behavior of Steam Pipe Steels: Effects of

Inclusion Content and Primary Creep, Eng. Fract. Mech., Vol 57, 1997, p 105–130

Creep Crack Growth Testing

B.E. Gore, Northwestern University, W. Ren, Air Force Materials Laboratory, P.K. Liaw, The University of Tennessee

Acknowledgments

B.E. Gore is thankful for the support of the University of Tennessee, Knoxville, especially her fellow group

members, Dr. Yuehui He, Bing Yang, Liang Jiang, J.T. Broome, Glen Porter, and Leslie Miller. P.K. Liaw is

grateful for the financial support provided by the National Science Foundation (DMI-9724476 and EEC-

9527527 with Dr. D. Durham and Ms. M. Poats as contract monitors, respectively).

Creep Crack Growth Testing

B.E. Gore, Northwestern University, W. Ren, Air Force Materials Laboratory, P.K. Liaw, The University of Tennessee

References

1. W. Ren, “Time-Dependent Fracture Mechanics Characterization of Haynes HR160 Superalloy,” Ph.D.

dissertation, School of Material Science and Engineering, University of Tennessee, 1995

2. H. Riedel and J.R. Rice, Tensile Cracks in Creep Solids, Fracture Mechanics: Twelfth Conf., STP 700,

ASTM, 1980, p 112–130

3. M. Okazaki, I. Hattori, F. Shiraiwa, and T. Koizumi, Effect of Strain Wave Shape on Low-Cycle

Fatigue Crack Propagation of SUS 304 Stainless Steel at Elevated Temperatures, Metal. Trans. A, Vol

14, 1983, p 1649–1659

4. A. Saxena and P.K. Liaw, “Remaining Life Estimations of Boiler Pressure Parts—Crack Growth

Studies,” Final Report CS 4688 per EPRI Contract RP 2253-7, Electric Power Research Institute, 1986

5. R.H. Norris, P.S. Grover, B.C. Hamilton, and A. Saxena, Elevated Temperature Crack Growth, Fatigue

and Fracture, Vol 19, ASM Handbook, ASM International, 1996

6. A. Saxena, “Life Assessment Methods and Codes,” EPRI TR-103592, Electric Power Research

Institute, 1996

7. A. Saxena, “Recent Advances in Elevated Temperature Crack Growth and Models for Life Prediction,”

Advances in Fracture Research: Proc. Seventh Int. Conf. on Fracture, March 1989 (Houston, TX), K.

Salama, K. Ravi-Chander, D.M.R. Taplin, and P. Rama Rao, Ed., Pergamon Press, 1989, p 1675–1688

8. W.A. Logsdon, P.K. Liaw, A. Saxena, and V.E. Hulina, Residual Life Prediction and Retirement for

Cause Criteria for Ships Service Turbine Generator (SSTG) Upper Casings, Part I: Mechanical Fracture

Mechanics Material Properties Development, Eng. Fract. Mech., Vol 25, 1986, p 259–288

9. P.K. Liaw, A. Saxena, and J. Schaefer, Predicting the Life of High-Temperature Structural Components

in Power Plants, JOM, Feb 1992

10. J.T. Staley, Jr., “Mechanisms of Creep Crack Growth in a Cu-1 wt. % Sb Alloy,” MS thesis, Georgia

Institute of Technology, 1988

11. J.L. Bassani and V. Vitek, Proc. Ninth National Congress of Applied Mechanics—Symposium on Non-

Linear Fracture Mechanics, L.B. Freund and C.F. Shih, Ed., American Society of Mechanical

Engineers, 1982, p 127–133

12. A. Saxena, Fracture Mechanics Approaches for Characterizing Creep-Fatigue Crack Growth, Int. J.

JSME A, Vol 36 (No. 1), 1993, p 15, 16

13. J.D. Landes and J.A. Begley, A Fracture Mechanics Approach to Creep Crack Growth, Mechanics of

Crack Growth, STP 590, ASTM, 1976, p 128–148

14. K.M. Nikbin, G.A. Webster, and C.E. Turner, Relevance of Nonlinear Fracture Mechanics to Creep

Cracking, Cracks and Fracture, STP 601, ASTM, 1976, p 47–62

15. S. Taira, R. Ohtani, and T. Kitamura, Application of J-integral to High-Temperature Crack Propagation,

J. Eng. Mater. Technol. (Trans. ASME), Vol 101, 1979, p 154

16. V. Kumar, M.D. German, and C.F. Shih, “An Engineering Approach to Elastic-Plastic Analysis,”

Technical Report EPRI NP-1931, Electric Power Research Institute, 1981

17. J. Hutchinson, Singular Behavior at the End of a Tensile Crack in a Hardening Material, J. Mech. Phys.

Solids, Vol 16, 1968, p 13

18. J. Rice and G.F. Rosengren, Plane Strain Deformation near a Crack Tip in a Power-Law Hardening

Material, J. Mech. Phys. Solids, Vol 16, 1968, p 1–12

19. N.L. Goldman and J.W. Hutchinson, Fully Plastic Crack Problems: The Center-Cracked Strip Under

Plane Strain, Int. J. Solids Struct., Vol 11, 1975, p 575–591

20. C.P. Leung, D.L. McDowell, and A. Saxena, Consideration of Primary Creep at Stationary Crack Tips:

Implications for the C

Parameter, Int. J. Fract., Vol 36, 1988

21. A. Saxena, Creep Crack Growth in Creep-Ductile Materials, Eng. Fract. Mech., Vol 40 (No. ), 1991, p

721

22. P.K. Liaw, A. Saxena, and J. Schaefer, Estimating Remaining Life of Elevated Temperature Steam

Pipes, Part I: Material Properties, Eng. Fract. Mech., Vol 32, 1989, p 675

23. “Standard Test Method for Measurement of Creep Crack Growth Rates in Metals,” ASTM E 1457,

American Society for Testing and Materials, 1998

24. H. Riedel, Creep Deformation at Crack Tips in Elastic-Viscoelastic Solids, J. Mech. Phys. Solids, Vol

29, 1981, p 35

25. K. Ohji, K. Ogura, and S. Kubo, Stress-Strain Field and Modified J-Integral in the Vicinity of a Crack

Tip Under Transient Creep Conditions, Int. J. JSME, Vol 790 (No. 13), p 18, 1979

26. J.D. Bassani and F.A. McClintock, Creep Relaxation of Stress Around a Crack Tip, Int. J. Solids Struct.,

Vol 7, 1981, p 479

27. R. Ehlers and H. Riedel, A Finite Element Analysis of Creep Deformation in a Specimen Containing a

Macroscopic Crack, Advances in Fracture Research: Proc. of the Fifth Int. Conf. of Fracture, ICF-5

,Vol 2, Pergamon Press, 1981, p 691–698

28. J.L. Bassani, K.E. Hawk, and A. Saxena, Evaluation of the C

Parameter for Characterizing Creep Crack

Growth Rate in the Transient Regime, Time-Dependent Fracture, Vol 1, Nonlinear Fracture

Mechanics, STP 995, ASTM, 1986, p 7–26

29. H. Riedel and V. Hetampel, Creep Crack Growth in Ductile, Creep Resistant Steels, Int. J. Fract., Vol

34, 1987, p 179

30. D.L. McDowell and C.P. Leung, Implication of Primary Creep and Damage for Creep Crack Extension

Criteria, Structural Design for Elevated Temperature Environments—Creep, Ratchet, Fatigue and

Fracture, Pressure Vessel and Piping Division, Vol 163, July 23–27 1989 (Honolulu), American

Society of Mechanical Engineers

31. A. Saxena, Creep Crack Growth Under Nonsteady-State Conditions, ASTM STP 905, Seventeenth

ASTM National Symposium on Fracture Mechanics, American Society for Testing and Materials, 1986,

p 185–201

32. B.E. Jaske and J.A. Begley, An Approach to Assessing Creep/Fatigue Crack Growth, Ductility and

Toughness Considerations in Elevated Temperature Service, MPC-8, ASTM, 1978, p 391

33. S. Taira, R. Ohtani, and T. Komatsu, Application of J-Integral to High Temperature Crack Propagation,

Part II: Fatigue Crack Propagation, J. Eng. Mater. Technol. (Trans. ASME), Vol 101, 1979, p 162

34. R. Ohtani, T. Kitamura, A. Nitta, and K. Kuwabara, High-Temperature Low Cycle Fatigue Crack

Propagation and Life Laws of Smooth Specimens Derived from the Crack Propagation Laws, STP 942,

H. Solomon, G. Halford, L. Kaisand, and B. Leis, Ed., ASTM, 1988, p 1163

35. K. Kuwabara, A. Nitta, T. Kitamura, and T. Ogala, Effect of Small-Scale Creep on Crack Initiation and

Propagation under Cyclic Loading, STP 924, R. Wei and R. Gangloff, Ed., ASTM, 1988, p 41

36. R. Ohtani, T. Kitamura, and K. Yamada, A Nonlinear Fracture Mechanics Approach to Crack

Propagation in the Creep-Fatigue Interaction Range, Fracture Mechanics of Tough and Ductile

Materials and Its Application to Energy Related Structures, H. Liu, I. Kunio, and V. Weiss, Ed.,

Materials Nijhoff Publishers, 1981, p 263

37. K. Ohji, Fracture Mechanics Approach to Creep-Fatigue Crack Growth in Role of Fracture Mechanics

in Modern Technology, Fukuoka, Japan, 1986

38. K.B. Yoon, A. Saxena, and P.K. Liaw, Int. J. Fract., Vol 59, 1993, p 95