Арменский Е.В., Фалк Г.Б. ??Электромеханические устройства автоматики

–61–

сигнала принимают sinβ. При sinβ = 1 поле статора круговое; при (1 > sinβ

> 0) – эллиптическое, при sinβ = 0 – пульсирующее.

Амплитудно - фазовый способ управления с конденсатором в цепи

возбуждения (конденсаторный) (рис. 2.20,а). Обмотку управления У

подключают к сети переменного тока через регулятор напряжения;

напряжение управления U

y

совпадает по фазе с напряжением сети U

1

.

Сдвиг по фазе тока, а, следовательно, и напряжения на обмотке

возбуждения по отношению к обмотке управления осуществляется

конденсатором, который включают последовательно с обмоткой

возбуждения. Управление двигателем производится за счет изменения

амплитуды напряжения управления.

Рис. 2.20

Причем, несмотря на то, что фаза напряжения управления не

изменяется (совпадает с фазой напряжения сети), при

изменении

напряжения управления наблюдается одновременное изменение как

амплитуды, так и фазы напряжения на обмотке возбуждения U

в

(рис. 2.20,

б). Такое же явление наблюдается и при изменении угловой скорости

ротора за счет изменения момента нагрузки при неизменном напряжении

управления. Это объясняется тем, что напряжение возбуждения U

в

равно

геометрической разности напряжений сети и на конденсаторе

•

вU

=

•

1

U

-

•

Uc .

–62–

Напряжение на конденсаторе U

c

при изменении напряжения

управления или угловой скорости ротора меняется вследствие изменения

тока в цепи возбуждения, который является функцией скольжения и

коэффициента сигнала:

•

Uc

= - j

•

вI

х

с.

Следовательно, меняется по

амплитуде и фазе напряжение на обмотке возбуждения U

в.

Поскольку круговое поле существует в двигателе только при

соблюдении условия

•

Uв

= j 'Uу

•

, при заданном значении емкости

конденсатора в цепи возбуждения круговое поле возможно только при

строго определенном коэффициенте сигнала

α

0

= U

y0

/U

1

и определенном

значении скольжения s. Конкретные значения напряжения управления и

емкости конденсатора, обеспечивающие круговое поле при заданном

скольжении, определяют расчетным или экспериментальным путем. В

паспортах исполнительных асинхронных микродвигателей эти данные

наиболее часто указывают для режима пуска (s=1).

Реверсирование исполнительных асинхронных микродвигателей

при амплитудном и конденсаторном способах управления производят

изменением фазы напряжения управления на 180

°, например, путем

переключения выводов обмотки У. При фазовом и пространственном

способах управления реверсирование осуществляют изменением знака

угла

β или γ. В любом из рассмотренных случаев поле статора начинает

вращаться в противоположную сторону и изменяется направление

вращения ротора.

Электромагнитный момент. Форма магнитного поля в двигателе в

общем случае эллиптическая, причем эллиптичность вызвана асимметрией

МДС обмоток В и У. Поскольку в большинстве исполнительных

двигателей угол между обмотками

γ,=90°, то можно перейти от

асимметрии МДС к асимметрии приведенных токов в обмотках В и У

статора двигателя. Это значит, что угол сдвига

β векторов I

в

и I

y

во времени

отличен от 90

°, а значения модулей, приведенных к числу витков обмотки

возбуждения, не равны: I

y

′= I

y

/К

т

. ≠ I

в.

Для того чтобы при определении токов и вращающего момента в

исполнительном микродвигателе можно было использовать методику

расчета асинхронных двигателей с симметричным питанием, приведенную

в §2.4, воспользуемся методом симметричных составляющих в

применении к двухфазным системам.

Согласно этому методу несимметричная двухфазная система

векторов токов I

в

и I

y

неодинаковой длины, сдвинутых между собой на

произвольный угол, может быть разложена на две симметричные системы,

состоящие каждая из двух векторов, одинаковых по длине и сдвинутых

между собой на угол 90

°. Система векторов прямой последовательности

(I

впр

, I′

yпр

) имеет то же чередование фаз, что и исходная система. Система

–63–

векторов обратной последовательности (I

вобр

, I′

yобр

) имеет

противоположное чередование фаз. При этом

•

I

упр

= -j

•

I

впр

;

•

I

уобр

= j

•

I

вобр

.

(2.35)

Эквивалентность исходной и полученной систем имеет место, если

•

I

впр

+

•

I

вобр

=

•

I

в

;

•

I

′

yпр

+

•

I

′

yобр

=

•

I

′

y

. (2.36)

Составляем схемы замещения двигателя, необходимые для

определения токов в обмотках статора и ротора. При одинаковой схеме

обмоток параметры схем замещения фаз В и У в приведенной форме

практически равны и схему замещения достаточно составить только для

фазы В.

–64–

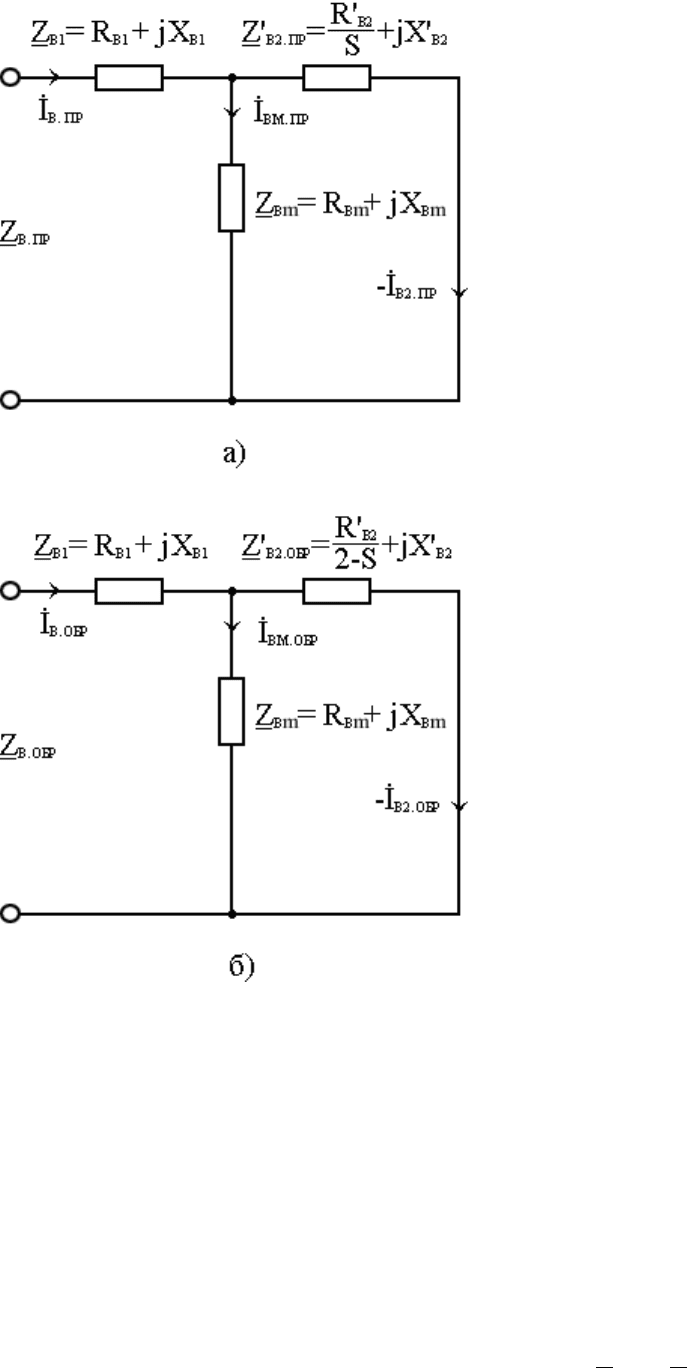
Рис. 2.21

Схемы замещения составляют по аналогии со схемой замещения

трехфазного асинхронного двигателя (рис. 2.10), но раздельно для прямой

(рис. 2.21,а) и обратной (рис. 2.21,б) последовательностей, поскольку поля

прямой и обратной последовательностей вращаются относительно ротора с

разной скоростью, что определяет выражения для скольжения и значения

полных сопротивлений в схемах замещения.

На рис

. 2.21: R

в1

и Х

в1

- активное и индуктивное сопротивления

статорной обмотки; R

′

в2

и Х′

в2

– активное и индуктивное сопротивления

ротора, приведенные к числу фаз статора и числу витков обмотки В; R

вm

и

Х

вm

– активное и индуктивное сопротивления фазы, соответствующие

магнитному потоку взаимоиндукции статора и ротора; Z

впр

и Z

вобр

– полное

–65–

сопротивление схемы замещения для прямой и обратной

последовательностей.

Если в цепь обмотки возбуждения двигателя включают

последовательно фазосдвигающий элемент, то его сопротивление Z

ф

должно быть введено в статорный участок схемы замещения фазы В, т.е.

последовательно с Z

в1

. При этом методика расчета токов и вращающего

момента не изменяется, однако расчетные уравнения несколько

усложняются.

Напряжения, подаваемые на обмотки возбуждения и управления,

уравновешиваются падениями напряжения от токов обеих

последовательностей на сопротивлениях соответствующих схем

замещения, т.е.

•

U

1

=

•

I

впр

(Z

впр

+ Z

ф

) +

•

I

вобр

(Z

вобр

+ Z

ф

), (2.37)

•

U

y

′ =

•

I

′

yпр

Z

впр

+

•

I

′

yобр

Z

вобр

.

Решая систему (2.37) с учетом (2.35), получаем выражения

симметричных составляющих токов фаз I

впр

и I

вобр

и по схемам замещения

(см. рис. 2.21) определяем симметричные составляющие тока ротора I

в2пр

и

I

в2обр

.

Для определения электромагнитных моментов прямой М

пр

и

обратной М

обр

последовательностей исполнительного асинхронного

микродвигателя можно воспользоваться выражением (2.21), так как

вращающиеся магнитные поля прямой и обратной последовательностей

образованы симметричными системами токов :

М

пр

=

s

RI

ВПРВ

1

2

)(2

ω

′′

, (2.38)

М

обр

=

)2(

)(2

1

2

s

RI

ВОБРВ

−

′′

ω

.

Результирующий электромагнитный момент равен разности

моментов прямой и обратной последовательностей:

М

эм

= М

пр

– М

обр

. (2.39)

Статические характеристики. Механические и регулировочные

характеристики исполнительных асинхронных микродвигателей в

относительных единицах представлены на рис. 2.22 (скорость в

–66–

Рис.2.22а

относительных единицах ω

∗

= ω

2

/ ω

1

= 1 – s; момент в относительных

единицах М

∗

= М

эм

/ М

по

, где М

п0

– пусковой момент при круговом поле). В

качестве примера характеристики построены для амплитудного способа

управления.

Анализ механических характеристик по уравнениям момента (2.38) –

(2.39) показывает, что при всех способах управления характеристики

нелинейны и их жесткость уменьшается с уменьшением сигнала

управления (см. рис. 2.22а). Повышению линейности механических

характеристик способствует увеличение активного сопротивления ротора.

Однако, как

известно, увеличение активного сопротивления ротора

ухудшает энергетические показатели двигателя. У исполнительных

асинхронных микродвигателей, работающих в системах автоматики,

допускается нелинейность порядка 10%.

Наиболее линейными являются характеристики при фазовом способе

управления; причем жесткость характеристик мало меняется при

изменении коэффициента сигнала. Наименее линейны механические

характеристики при амплитудно - фазовом способе управления. При всех

способах управления

механические характеристики обеспечивают

устойчивость работы во всем диапазоне двигательного режима и с

уменьшением коэффициента сигнала смещаются в сторону меньших

моментов и скоростей.

–67–

Рис. 2.22б

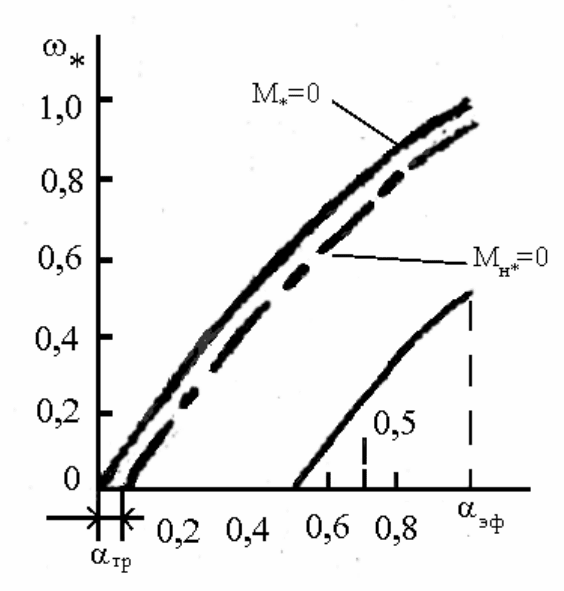
Анализ регулировочных характеристик показывает ( рис. 2.22б), что

при всех способах управления они в общем нелинейны. Наибольшая

нелинейность – в режиме холостого хода и зависит в основном от тех же

параметров двигателя, что и нелинейность механических характеристик.

Ближе всех к линейным характеристики микродвигателей с фазовым

способом управления, затем следует амплитудный

и амплитудно - фазовый

способы. Наибольшую линейность и крутизну характеристики имеют в

начальной части, поэтому для обеспечения линейности регулирования

двигатель должен работать при малых сигналах и относительных

скоростях. Уменьшение относительных скоростей наиболее эффективно

достигается повышением рабочей частоты напряжения питания двигателя,

так как при этом пропорционально повышается синхронная угловая

скорость. При нелинейности

механических характеристик меньше 10%

степень нелинейности регулировочной характеристики холостого хода не

превышает 20% в диапазоне изменения коэффициента сигнала 0

÷ 0.7

У исполнительных асинхронных микродвигателей в режиме

реального х.х. (М

н∗

=0) регулировочная характеристика выходит не из нуля

(пунктирная линия на рис.2.22б). Объясняется это тем, что ротор начнет

вращаться только при сигнале, называемом сигналом трогания

α

тр

, при

котором электромагнитный момент двигателя превысит момент трения

покоя на валу двигателя. Значение сигнала трогания, определяющего зону

нечувствительности исполнительного микродвигателя, не должно

превышать 0,05.

Рассмотренные способы управления обеспечивают весьма широкий

диапазон регулирования. У исполнительных микродвигателей с полым

–68–

немагнитным ротором он достигает D=(100÷200):1. Пусковой момент при

всех способах управления прямо пропорционален сигналу управления и в

относительных единицах равен эффективному коэффициенту сигнала.

Анализ мощности управления P

y

=U

y

I

y

cosϕ

y

показывает, что при

амплитудном и амплитудно-фазовом способах управления она примерно

одинаковая и с уменьшением сигнала уменьшается примерно

пропорционально квадрату коэффициента сигнала. При фазовом способе

управления эта мощность с уменьшением коэффициента сигнала

практически не меняется. В этом отношении амплитудный и амплитудно-

фазовый способы управления имеют существенное преимущество перед

фазовым. КПД

исполнительных асинхронных микродвигателей несколько

ниже, чем у одинаковых по мощности асинхронных микродвигателей

общего применения, из-за повышенного активного сопротивления ротора.

Среди схем питания исполнительных асинхронных микродвигателей

наибольшей простотой отличается схема конденсаторного

микродвигателя, так как она не имеет сложных устройств для сдвига по

фазе напряжений управления и возбуждения.

Таким образом, амплитудно-фазовый

способ управления с

конденсатором в цепи возбуждения двигателя имеет ряд преимуществ;

поэтому его широко применяют в схемах автоматики. Однако в каждом

конкретном случае выбор способа управления должен определяться

условиями работы системы, звеном которой является двигатель, и

требованиями, предъявляемыми к этому звену.

Динамические характеристики. Динамические характеристики

представляют собой временные зависимости и показатели, определяющие

качество работы исполнительных двигателей в переходных режимах: при

пуске, торможении, реверсировании и регулировании скорости. К числу

важнейших динамических показателей относится быстродействие –

способность развивать заданную угловую скорость ротора с минимальным

запаздыванием во времени по отношению к соответствующему изменению

электрического сигнала.

У исполнительных

микродвигателей время электромагнитных

переходных процессов, связанных с индуктивностью обмоток, значительно

меньше времени электромеханических переходных процессов, связанных с

моментом инерции ротора. Поэтому на начальном этапе анализа

динамических характеристик электромагнитными переходными

процессами можно пренебречь и провести этот анализ на основе уравнения

равновесия моментов (2.29). Для упрощения анализа принимаем М

ст

=0,

тогда

( 2.40)

.

d

t

Jd

M

эм

ω

=

–69–

Однако механические характеристики исполнительных асинхронных

микродвигателей нелинейные и для получения передаточной функции

двигателя необходима их линеаризация.

Рис. 2.23

На рис. 2.23 сплошной линией показана механическая

характеристика при

произвольном коэффициенте сигнала α(при фазовом

управлении вместо

α можно подставить sinβ).

Если угловая скорость изменяется во всем диапазоне от нуля до

скорости холостого хода, то линеаризацию можно провести посредством

секущей АС (штрих-пунктирная линия на рис. 2.23). Это наиболее грубый

способ линеаризации, но он позволяет получить качественно наглядные и

достаточно точные результаты. При более точном анализе может

применяться кусочно-линейная аппроксимация механической

характеристики.

При выбранном нами способе линеаризации механическая

характеристика представляет собой прямую линию, проходящую через

точки скорости холостого хода

ω

оα

и пускового момента М

пα

,

соответствующие произвольному значению коэффициента сигнала.

Уравнение этой прямой линии при данном сигнале

α имеет вид

(2.41)

Подставим М

эм

из (2.41) в (2.40) и получаем дифференциальное уравнение

движение ротора:

(2.42)

).1(

οα

α

ω

−=

Пэм

ММ

.)(

οα

α

οα

ωω

ω

=+

П

M

J

dt

d

–70–

Решая уравнение(2.42)при нулевых начальных условиях (t=0, ω=0),

получаем переходную функцию двигателя:

ω = ω

оα

(1-е

-t/τм

). (2.43)

Рис. 2.24

График переходной функции

ω = f(t) изображен на рис. 2.24, а. Уравнение

экспоненты (2.43) и указанный график характеризуют, в частности,

переходный процесс при пуске двигателя. Величина

τ

м

входящая в

выражение (2.43) - это электромеханическая постоянная времени

двигателя, равная коэффициенту при производной от угловой скорости в

уравнении (2.42):

(2.44)

Поскольку выражение (2.43) является уравнением экспоненты, то

τ

м

- это время, в течение которого двигатель после подачи сигнала

управления развивает угловую скорость, равную 0,632 от установившегося

значения (это определение соответствует ГОСТу).

Физически величину

τ

м

можно представить как время, в течение

которого ротор ненагруженного двигателя разгоняется от неподвижного

состояния до скорости идеального холостого хода при неизменном

вращающем моменте, равном пусковому. Практическое время разгона, за

которое ротор достигает скорости 0,95-0,98 от заданной, составляет (3

÷4)

τ

м

.

Уравнение (2.42) в операторной форме имеет вид:

.

α

οα

ω

τ

П

м

M

J=

Арменский Е.В., Фалк Г.Б. ??Электромеханические устройства автоматики

Подождите немного. Документ загружается.