Арефьев К.П., Нагорнова А.И. и др. Высшая математика. Часть 1
Подождите немного. Документ загружается.


5.3. Основные правила дифференцирования
181
x
y
2
sin
1
−=
′
,
где n
x
π≠ , п ∈ Z.
Доказательство. Воспользуемся формулой
x
x
x
sin
cos
ctg = и теоремой
3.
Тогда
=
⋅−⋅−
=
′
−
′
=
′
x
xxxx
x
xxxx
y
22
sin
coscossinsin
sin
cos)(sinsin)(cos
xx
xx
22
22
sin
1
sin
cossin
−=
+
−=
.
Следовательно,
x
y
2
sin
1
−=
′
.
Производная логарифмической функции. Производная
функции
xy
a
log= , где а > 0, a ≠ 1, х > 0, выражается формулой
ax
y
ln
1
=
′
.
Доказательство. Придадим фиксированному значению х ∈ D(y)
приращение Δх. Тогда
⎟
⎠
⎞
⎜
⎝
⎛
Δ
+=
Δ+
=−Δ+=Δ
x
x
x
xx
xxxy
aaaa
1logloglog)(log .
Найдём по определению y
′
:
=
⎟
⎠
⎞
⎜
⎝
⎛
Δ
+=
Δ
⎟
⎠
⎞
⎜
⎝
⎛
Δ
+
=
Δ
Δ
=
′
Δ
→Δ→Δ→Δ
x
x
a
x
a
xx
x
x
xx
x
x
x
y
y 1loglim
1
1log
limlim
000
ax
e
xx
x
x
a
x
x
x
a
ln
1
log
1
1limlog
1
0
==
⎟
⎠
⎞
⎜
⎝
⎛
Δ
+=
Δ
→Δ
.
Здесь мы воспользовались вторым замечательным пределом
()
ex
x
x
=+
→
1
0
1lim и формулой
a
x
x
b
b
a
log
log
log = .
Таким образом,
ax
y
ln
1
=
′
.

Глава 5. Дифференцирование функции одной переменной
182
Замечание.
В частности, при а = е, производная функции у = lnx на-
ходится по формуле
x
y
1
=
′
.
Производная степенной функции. Производная функции
α
= xy , где α ∈ R, выражается формулой
1
−
α
α=
′
xy .
Доказательство. Пусть х > 0. Прологарифмируем обе части равен-
ства
α
= xy по основанию е:
α
= xy lnln , или
x
y lnln
α
=
.
Продифференцируем полученное равенство почленно по правилу
дифференцирования сложной функции, считая у функцией от х (см. форму-
лу 5.1.10):
1
)ln()(ln
−α
α
α=⇒
α
=
′
⇒
α
=
′
⇒
α
=
′
⇒
′
α=
′
xy
x
x
y
x
y
y
xy
y
xy
.
Производная показательной функции. Производная функции
x
ay = , где а > 0, a ≠ 1, выражается формулой
aay
x
ln=
′
.
Доказательство. Имеем
(
)
1−=−=−=Δ
Δ
Δ
Δ
+
xxxxxxxx
aaaaaaay .
Таким образом,
=
Δ
Δ
=
Δ
−
=
Δ
⎟
⎠
⎞
⎜
⎝
⎛
−
Δ
=
Δ
Δ
=
′
→Δ
Δ
→Δ→Δ→Δ
x
ax
a
x
a
a
x
x
aa
x
y
y
x
x
x
x
x
x
xx
ln
lim
1
lim
1
limlim
0000
aa
x
ln
⋅
=
.
При вычислении предела воспользовались эквивалентностью беско-
нечно малых:
1
−
Δx
a ∼ Δхlna при Δх → 0.
В частности, при а = е производная функции
x
ey = выражается фор-
мулой
x
ey =
′
.
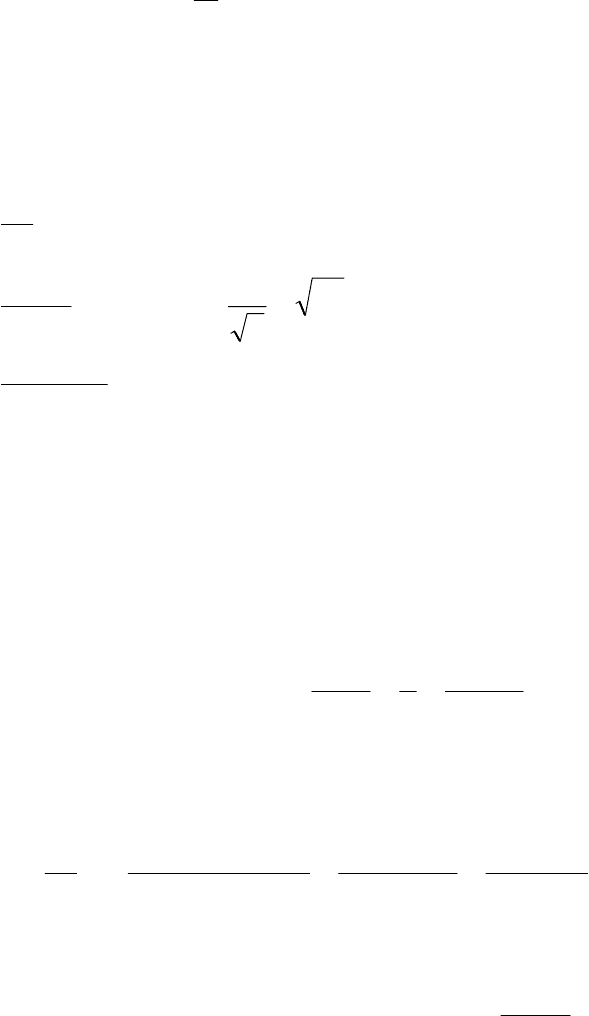
5.3. Основные правила дифференцирования
183
Приведём ещё один вывод данной формулы. Прологарифмируем вы-
ражение
x
ay = по основанию е:
axyay
x
lnlnlnln =⇒= .
Дифференцируем левую и правую часть полученного равенства по
правилу дифференцирования сложной функции, считая у функцией от х.
Тогда
aayayya
y
y
x
lnlnln =
′
⇒=
′
⇒=
′
.
Окончательно aaa
xx
ln)( =
′
.
Пример 6. Найти производные следующих функций:
6.1. xxxxf sin5cos34)(
3
+−= ; 6.2. xxxf lnlog)(
2
+
=
;
6.3.
x
e
xf
x
=)( ; 6.4. xxxf ctg)(
2
⋅= ;
6.5.
1
1
)(
2
2
+
−
=
x
x
xf ; 6.6.
3
3
1
)( x
x
xf += ;
6.7.
x
x
xf
sin21
cos
)(
+
= ; 6.8. 153)(
3
−++= xxxf
x
.
Решение. 6.1. Применяя правило дифференцирования суммы, получа-
ем
=
′
+
′
−
′
=
′
+−=
′
)sin5()cos3()4()sin5cos34()(
33
xxxxxxxf
x
x
x
cos5sin312
2
+
+
= .
6.2. Применяя правило дифференцирования суммы, получаем
2ln
2ln11
2ln
1
)(ln)(log)(
2
xxx
xxxf
+
=+=
′
+
′
=
′
.
6.3. Применяя правило дифференцирования частного функций, получа-
ем
222
)1()(
)(
x
xe
x
exe
x
exxe
x
e
xf
xxxxxx
−
=
−⋅
=
⋅
′
−⋅
′
=
′
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
′
.
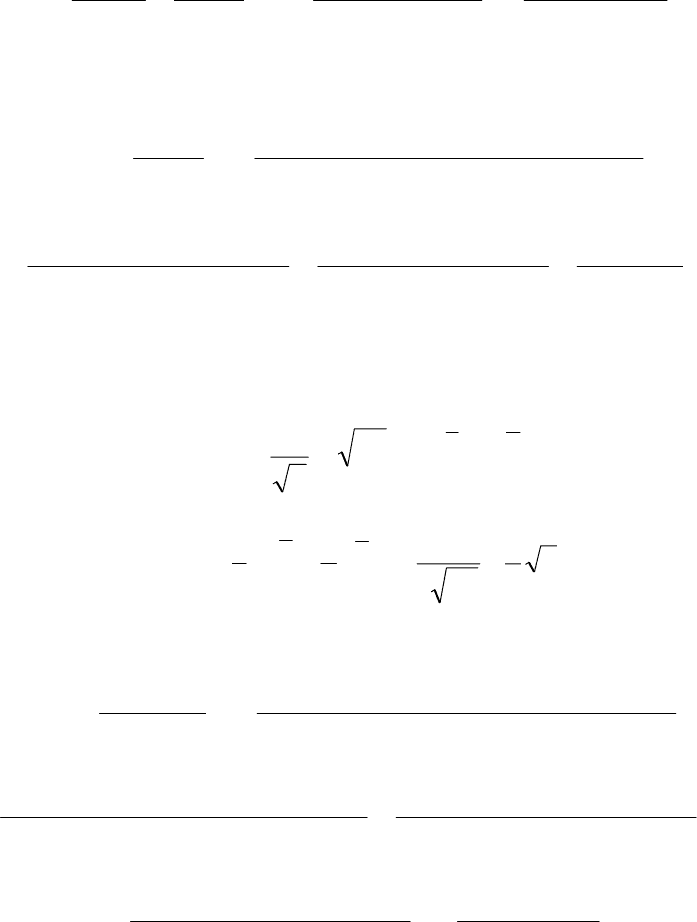
6.4. По правилу дифференцирования произведения получаем
=⋅−=
′
+
′
=
′
⋅=
′
2
2
222
sin
1
ctg2)ctg(ctg)()ctg()( x
x
xxxxxxxxxf
Глава 5. Дифференцирование функции одной переменной
184
x
xxx
x
xxx
x
x
x
x
x
x
222
sin
)2(sin
sin
sincos2
sin
sin
cos2 −
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
.
6.5. По правилу дифференцирования частного получаем
=
+
−
′
+−+
′
−
=
′
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
−
=
′
22
2222
2
2
)1(
)1()1()1()1(
1
1
)(
x
xxxx
x
x
xf
2222
33
22
22
)1(
4
)1(
2222
)1(
)1(2)1(2
+
=
+
+−+
=
+
−−+
=
x
x
x
xxxx
x
xxxx
.
6.6. Преобразуем функцию и применим правило дифференцирования
суммы:
2
3
3
1
3
3
1
)( xxx
x
xf +=+=
−
,
x
x
xxxf
2
3
3
1
2
3
3
1
)(
3
4
2
1
3
4
+−=+−=
′
−
.
6.7. По правилу дифференцирования частного получаем
=
+
′
+−+
′
=
′
⎟
⎠
⎞
⎜
⎝
⎛
+
=
′
2
)sin21(
cos)sin21()sin21()(cos
sin21
cos
)(
x
xxxx
x
x
xf
=
+
−−−
=
+
⋅−+−
=
2
22
2
)sin21(
cos2sin2sin
)sin21(
coscos2)sin21(sin
x
xxx
x
xxxx
22
22
)sin21(
2sin
)sin21(
)cos(sin2sin
x
x
x
xxx
+
+
−=
+
++
−=
.
6.8. По правилу дифференцирования суммы получаем
533ln3)1()5()()3()(
23
++=
′
−
′
+
′
+
′
=
′
xxxxf
xx
.
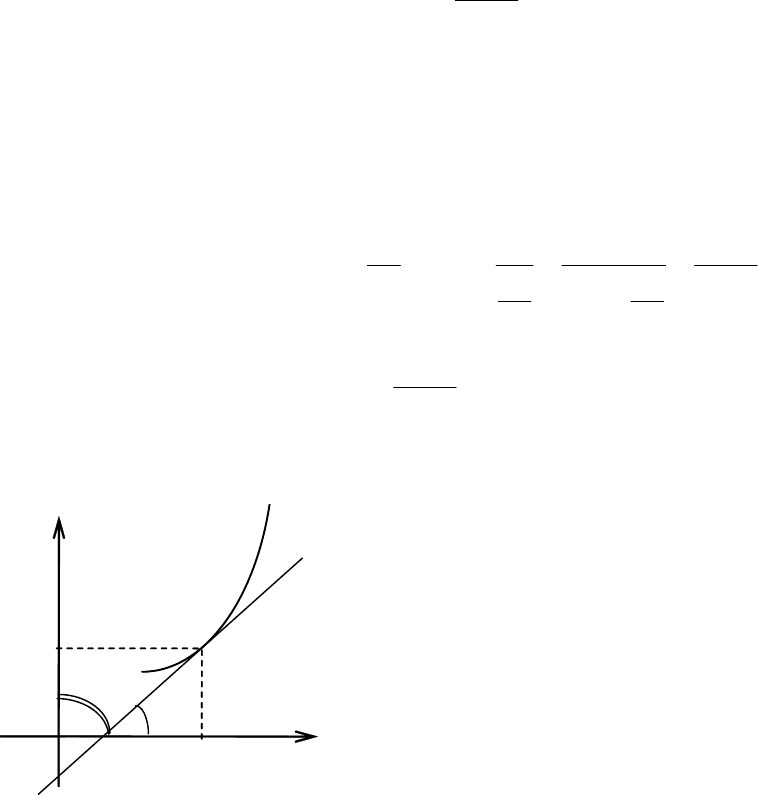
5.3. Основные правила дифференцирования
185
5.3.3. Производная обратной функции. Производные обратных
тригонометрических функций
Теорема 5.5 (о непрерывности обратной функции). Пусть
функция у = f(x) определена, строго монотонна и непрерывна на неко-
тором отрезке [a, b]. Тогда существует обратная функция х =
ϕ
(у),
которая является однозначной, непрерывной и монотонной на отрезке
[
α
,
β
].
Теорема 5.6 (о производной обратной функции). Если функция
у = f(x) монотонна на отрезке [a, b] и имеет во всех точках интервала
(а, b) ненулевую производную
)(xfy
′
=
′
, то обратная функция х =
ϕ
(у)
дифференцируема во всех точках интервала (f(a), f(b)), причём для лю-
бого у
∈
(f(a), f(b)) справедлива формула
)(
1
)(
xf
y
′
=ϕ
′
. (5.11)
Доказательство. Дадим фиксированному значению у обратной
функции х = ϕ(у) некоторое приращение Δу ≠ 0. Функция х = ϕ(у) получит
приращение Δх, причём в силу её монотонности Δх ≠ 0.
Найдём производную обратной функции. По определению производ-
ной имеем
)(
1
lim
11
limlim)()(
0
00
xf
x
y
x
y
y
x
yyx
x
xy
′
=
Δ
Δ
=
Δ
Δ
=
Δ
Δ
=ϕ
′
=
′
→Δ
→Δ→Δ
.
Таким образом, получаем
)(
1
)(
xf
y
′
=ϕ
′
.
Теорема доказана.
Теорема 5.6 имеет следующий геометрический смысл.
Рассмотрим в некоторой окрестности
точки
0
M график функции у = f(x) (рис. 5.7).
Производная
)(
0
xf
′
равна тангенсу угла α
наклона касательной, проходящей через точ-
ку
))(,(
00
xfxM
к оси Ох. Производная об-
ратной функции
)(
0
y
ϕ
′
равна тангенсу угла
β наклона этой касательной к оси Оу.
Производные обратных триго-
нометрических функций
С помощью формулы (5.11) найдём
y
y = f(x)
у
0
M
0
β α
O x
0
x
Рис. 5.7
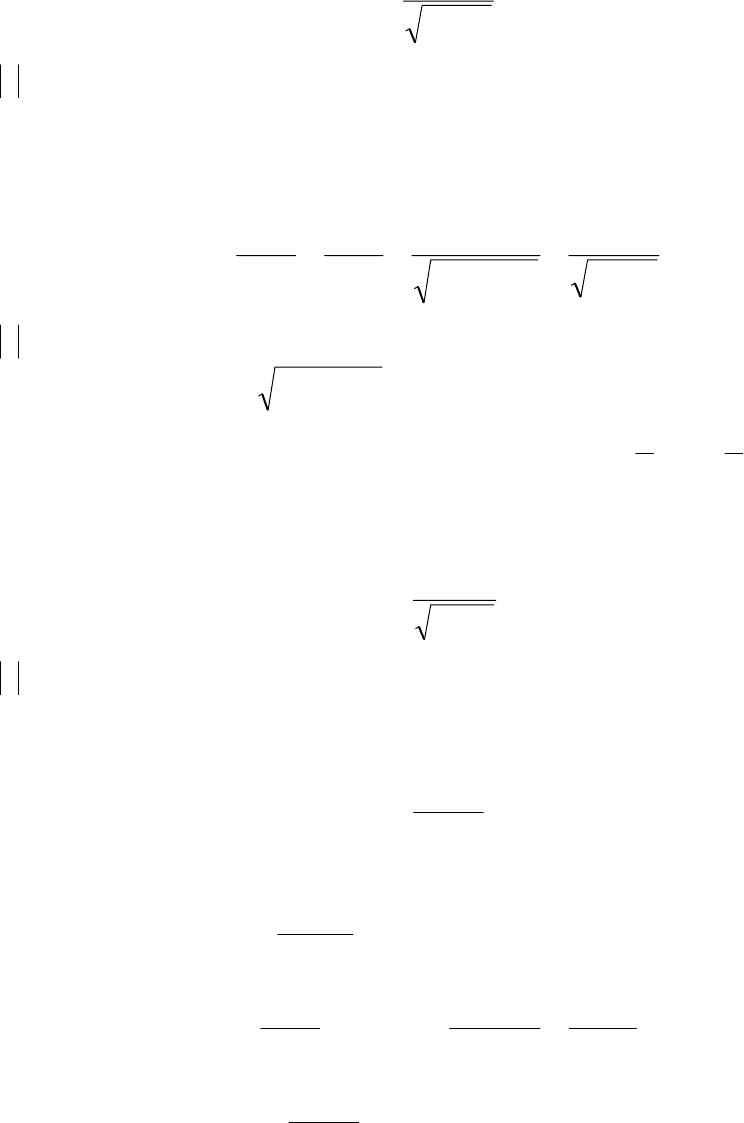
Глава 5. Дифференцирование функции одной переменной
186
производные обратных тригонометрических функций.
1. Производная функции у = arcsinx выражается формулой
2
1
1
)(
x
xy
−
=
′
,
где
1<x .
Доказательство. Рассмотрим обратную функцию х = sinу для
функции у = arcsinx. Так как
yyx cos)(
=
′
, то по теореме о производной об-
ратной функции получаем
22
1
1
sin1
1
cos
1
)(
1
)(
xy
yyx
xy
−
=
−
==
′
=
′
,
где
1<x .
В равенстве
yy
2
sin1cos −= перед корнем берём знак плюс, т. к.
функция у = arcsinx принимает значения на отрезке
22
π
≤≤
π
− y , следова-
тельно cosy ≥ 0.
2. Производная функции у = arcсоsx выражается формулой
2
1
1
)(
x
xy
−
−=
′
,
где
1<x .
Доказательство аналогично предыдущему.
3. Производная функции у = arctgx выражается формулой
2
1
1
)(
x
xy
+
=
′
.
Доказательство. Функция у = arctgx является обратной для функ-
ции х = tgу. Так как
y
yx
2
cos
1
)( =
′
, то имеем
22
2
1
1
tg1
1
cos
)(
1
)(
xy
y
yx
xy
+
=
+
==
′
=
′
.
Следовательно,
2
1
1
)(
x
xy
+
=
′
.
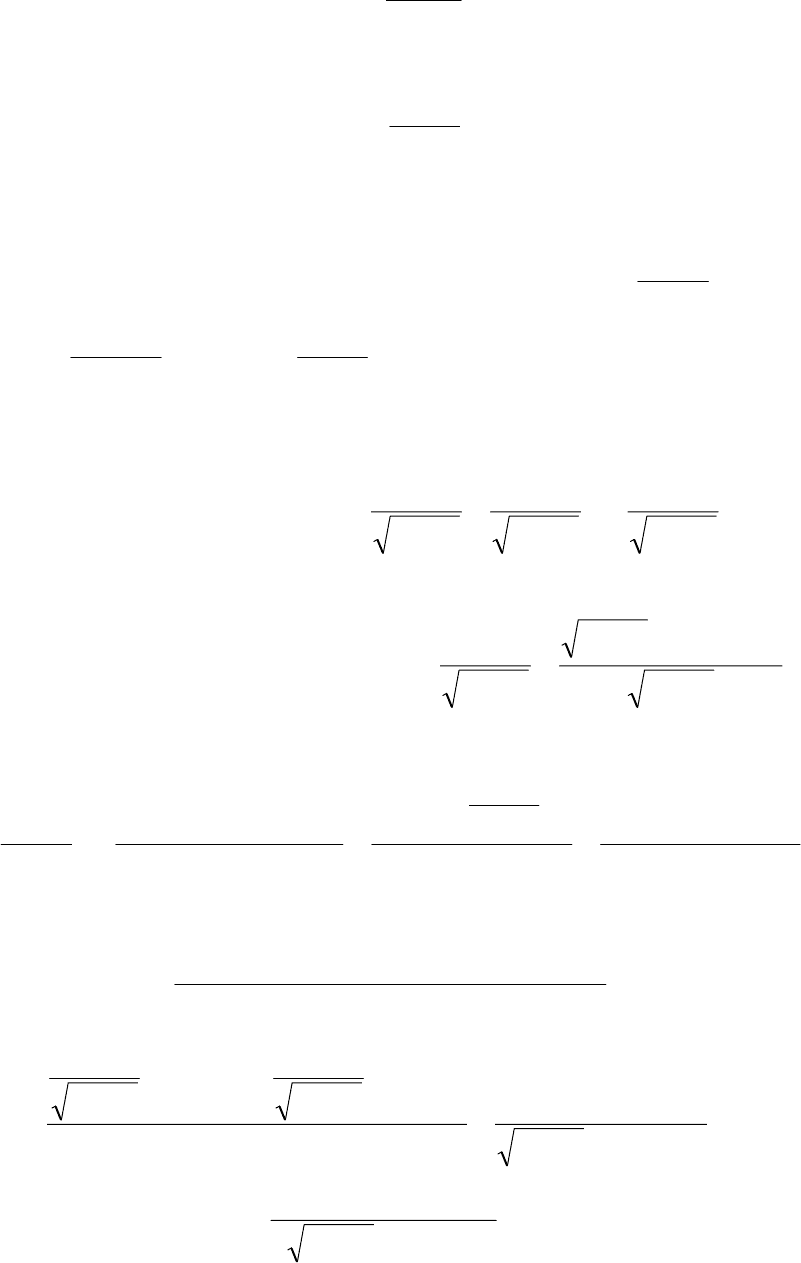
5.3. Основные правила дифференцирования
187
Здесь воспользовались формулой
y
y
2
2
tg1
cos
1
+=
.
4. Производная функции у = arcctgx выражается формулой
2
1
1
)(
x
xy
+
−=
′
.
Доказательство аналогично предыдущему.
Пример 7. Найти производные функций:
7.1. у = arcsinx + 5arccosx; 7.2. y = xarccosx; 7.3.
x
x
y
arctg
=
;
7.4.
x
x
y
arccos
arcsin
= ; 7.5.
x
x
x
y arctg
1
2
−
+
= ; 7.6.
x
x
x
y arctgsin
=
.
Решение. 7.1. Применяя правило дифференцирования суммы, полу-
чаем
222
1
4
1
5
1
1
)arccos5()(arcsin
xxx
xxy
−
−=
−
−
−
=
′
+
′
=
′
.
7.2. Применяя правило дифференцирования произведения, получаем
2
2
2
1
arccos1
1
arccos)(arccosarccos
x
xxx
x
x
xxxxxy
−
−−
=
−
−=
′
⋅+
′
=
′
.
7.3. Применяя правило дифференцирования частного, получаем
xx
xxx
x
x
x
x
x
xxxx
x
x
y
22
2
2
2
2
arctg)1(
arctg)1(
arctg
1
1
arctg
arctg
)arctg(arctg
arctg
+
−+
=
⋅
+
−
=
′
−
′
=
′
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
′
.
7.4. Применяя правило дифференцирования частного, получаем
=
′
−
′
=
′
2
)(arccos
arcsin)(arccosarccos)(arcsin
x
xxxx
y
=
⋅−
+
=
⋅
−
+⋅
−
=
xx
xx
x
x
x
x
x
22
2
22
arccos1
arcsinarccos
)(arccos
arcsin
1
1
arccos
1
1
xx
22
arccos12 ⋅−
π
= .

Глава 5. Дифференцирование функции одной переменной
188
7.5.
Применяя правило дифференцирования разности и частного, полу-
чаем
=
′
−
′
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
=
′
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
+
=
′
)arctg(
1
arctg
1
22
x
x
x
x
x
x
y
()()
(
)
(
)
=
+
−
+
−+
=
+
−
+
′
+−+
′
=
22
2
22
22
2
22
1
1
1
21
1
1
1
11
x
x
xx
x
x
xxxx
(
)
(
)
(
)
(
)
2
2
2
2
2
22
22
2
2
1
2
1
11
1
1
1
1
x
x
x
xx
x
x
x
+
−
=
+
+−−
=
+
−
+
−
= .
7.6. Применяя правило дифференцирования, получаем
(
)
(
)
(
)
=⋅
′
+
′
=
′
=
′
xxxxxxxxxy sinarctgarctgsinarctgsin
(
)
=
⋅
′
+
⋅
⋅
′
+
′
= xxxxxxxx sin)arctg(arctg)(sinsin
=⋅
+
+⋅+⋅= xx
x
xxxx sin
1
1
arctg)cossin1(
2
2
1
sin
arctgcosarctgsin
x
xx
xxxxx
+
+⋅⋅+⋅= .
Для удобства при решении примеров объединим полученные результа-
ты в таблицы:
• в табл. 1 приведены основные правила дифференцирования, где u(x),
v(x), f(x) – дифференцируемые функции, с = const;
• в табл. 2 собраны найденные производные основных элементарных
функций в п. 5.1.4, 5.1.5;
• в табл. 3 обобщены результаты табл. 2, используя правило диффе-
ренцирования сложной функции.
Таблица 1. Основные правила дифференцирования
1
ucuc
′
⋅=
′
⋅ )(
4
(
)
2
v
uvvu
v
u
′
−⋅
′
=
′
2
()
uvvuvu
′
+
′
=
′
⋅
5
[
]
(
)
)()()( xuxufxuf
u
x
′
⋅
′
=
′
3
()
vuvu
′
±
′
=
′
±
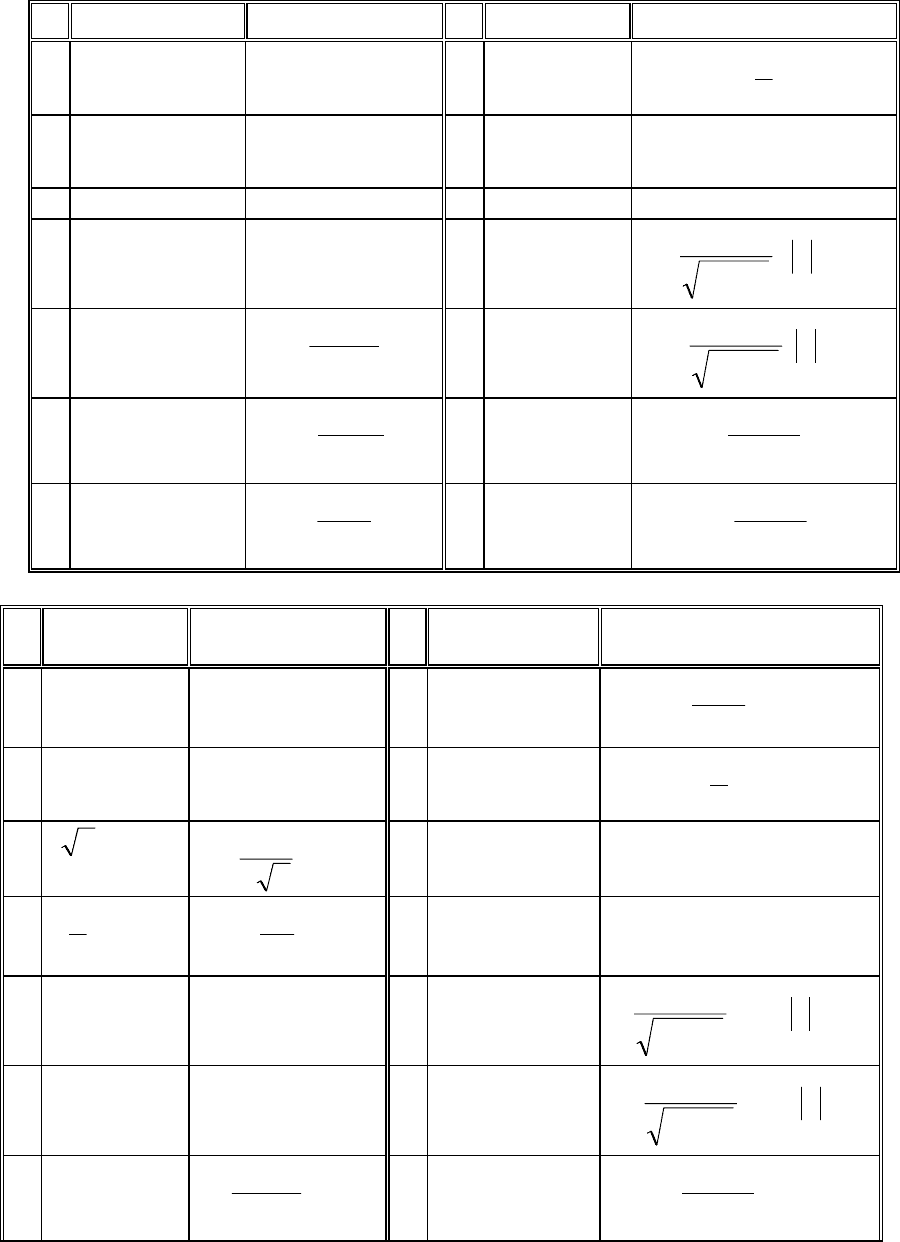
Таблица 2. Производные элементарных функций
5.3. Основные правила дифференцирования
189
№ Функция у(x)
y
′
(x)
№ Функция у(x)
y
′
(x)
1 с(с = const) 0 8 lnx
x
1
2
n
x
, где
п = const
1
−
n
nx
9
x
a , где
a > 0, a ≠ 1
x
a lna
3 cosx
−sinx
10 e
x
e
x
4 sinx cosx 11 arcsinx
2
1
1
x−
, 1<x
5 tgx
x
2
cos
1
12 arccosx
−
2
1
1
x−
, 1<x
6 ctgx
−
x
2
sin
1
13 arctgx
2
1
1
x+
7
()
0log >xx
a
;
a > 0, a ≠ 1
axln
1
14 arcctgx
−
2
1
1
x+
Таблица 3. Производные сложных функций
№ Функция
u = u(x)
Производная № Функция
u = u(x)
Производная
1 c(с = const) 0 9
(
)
0log >uu
a
a > 0, a ≠ 1
x
u
au
′
⋅
ln
1
2 и
п
x
n
uun
′
⋅⋅
−1
10
lnu,
0>u
x
u
u
′
⋅
1
3
u , 0≥u
x
u
u
′
⋅
2
1
11
u
a
a > 0, a ≠ 1
x
u
uaa
′
⋅ln
4
u
1
, 0≠u
x
u
u
′
⋅−
2
1
12 e
u
x
u
ue
′
⋅
5 cosu
x
uu
′
⋅− sin
13 arcsinu
x
u
u
′
⋅
−
2
1
1
, 1<u
6 sinu
x
uu
′
⋅cos
14 arccosu
x
u
u
′
⋅
−
−
2
1
1
, 1<u
7 tgu
x
u
u
′
⋅
2
cos
1
15 arctgu
x
u
u
′
⋅
+
2
1
1

Глава 5. Дифференцирование функции одной переменной
190
8 ctgu
x
u
u
′
⋅−
2
sin
1
16 arcctgu
x
u
u
′
⋅
+
−
2
1
1
Пример 8.
Используя правила дифференцирования, найти производ-
ные следующих функций:
8.1.
x
5
sin
1
; 8.2.
()
5
sincostg xxx −+ .
Решение. 8.1. Представим
55
sin
−
−
== uxy , где
x
u sin
=
,
xu
x
cos=
′
;
()
x
x
uuuuy
xx
u
x
6
65
sin
cos5
5
−
=
′
⋅−=
′
⋅
′
=
′
−−
.
8.2. Запишем функцию
у =
()
2
5
2
5
sincostg uxxx =−+ ,
где и = tgx + cosx – sinx,
xx
x
u
x
cossin
cos
1
2
−−=
′
,
xx
u
x
uuuuy
′
⋅=
′
⋅
′
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
=
′
2
3
2
5
2
5
.
Тогда
()
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−−−+⋅=
′
xx
x
xxxy
x
cossin
cos
1
sincostg
2
5
2
2
3
,
или
()
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−−⋅−+⋅=
′
xx
x
xxxy
x
cossin
cos
1
sincostg
2
5
2
3
.
Пример 9. Найти производные следующих функций:
9.1.
4
3
1+= xy
; 9.2. )13(cos
5
+= xy ;
9.3.
)1(sin
1
x
y
−
=
; 9.4.
)1(tg
5
+= xy ;
9.5. )21ln(
x
y
−
= ; 9.6.
)1(ln
2
10
+⋅
=
xx
y ;
9.7.
2
1
arcsin
x
y = ; 9.8.
x
g
ey
1
2
arct
= ;
