Арефьев К.П., Нагорнова А.И. и др. Высшая математика. Часть 1

Подождите немного. Документ загружается.

Односторонние пределы функции в точке. Классификация точек разрыва. Свойства функ-

ции, непрерывной на замкнутом промежутке

161

Определение 4.34. Если функция у = f(x) определена в некото-

рой окрестности точки а, но не определена в самой точке а, то она

называется

разрывной в точке а. При этом сама точка а, не являясь

точкой непрерывности, называется точкой разрыва функции у = f(x).

Существует несколько типов точек разрыва.

Определение 4.35. Точка х = а называется точкой разрыва

первого рода, если оба односторонних предела функции в этой точке

существуют и конечны, но не равны между собой

f(a − 0) ≠ f(a + 0) или

(

)

,lim

Axf

−→

(

)

,lim

Bxf

+→

где А

≠

В – некоторые числа.

Определение 4.36. Если х = а – точка разрыва первого рода,

то число

⎜

В – А

⎜

f(a + 0)

−

f(a

−

⎜

называется скачком функ-

ции

f(x) в точке а.

Определение 4.37. Точка х = а называется точкой устрани-

мого

разрыва, если односторонние пределы существуют и равны ме-

жду собой, но не равны значению функции в точке а, поскольку в самой

точке функция не определена, т е. выполняется равенство

f(a − 0) = f(a + 0) ≠ f(а).

Скачок функции в точке устранимого разрыва равен нулю.

Если доопределить функцию, положив f(а) = f

(a−0) = f(a+0), можно

восстановить непрерывность функции в точке a

Пример 21. Исследовать точки разрыва функции

()

sin

= .

Решение. Функция

()

sin

= определена на промежутке (−∞, 0) ∪ (0,

+∞) и, являясь элементарной, может иметь разрыв только в тех точках, где

она не определена, т. е. точка х = 0 является её единственной точкой разры-

ва. Найдём односторонние пределы функции в этой точке:

()

(

)

sin

lim

sin

lim0

−

=−

−→−→

()

sin

lim0

==+

+→

f(−0) = f(+0).

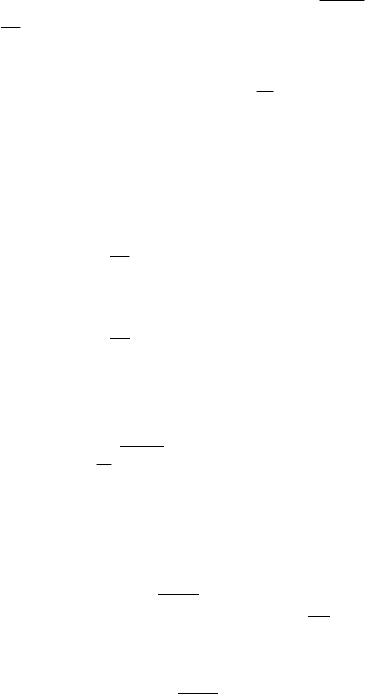
Глава 4. Введение в математический анализ

162

Односторонние пределы конечны и равны между собой в силу чётно-

сти функции.

Используя первый замечательный предел, доопределим функцию в

точке х = 0, положив значение функции в этой точке равное единице. Таким

образом, точка х = 0 является точкой устранимого разрыва.

Определение 4.38. Точка а называется точкой разрыва вто-

рого

рода, если хотя бы один из односторонних пределов функции в ней

не существует или равен бесконечности.

Пример 22. Исследовать функции на непрерывность:

22.1.

()

= sin ; 22.2.

()

−

xf .

Решение. 22.1.

Функция

()

= sin определена всюду кроме точки

х = 0. Функция является элементарной, следовательно, может иметь разрыв

только в тех точках, где она не определена. Найдём односторонние пределы

функции в точке х = 0:

()

∞+=

+→

sinsinlim

не существует;

()

∞−=

−→

sinsinlim

не существует.

Поэтому х = 0 – точка разрыва второго рода.

22.2. Функция

()

−

является элементарной и определена на

всей вещественной оси кроме точки х = 3. Чтобы определить род (тип) раз-

рыва, найдём односторонние пределы функции:

,022lim

===

∞

∞−

−

−→

.22lim

+∞==

∞

−

+→

Один из односторонних пределов равен +∞, следовательно, точка х

= 3

есть точка разрыва второго рода (рис. 4.30).

Сформулируем свойства функции, непрерывной на замкнутом проме-

жутке.

Односторонние пределы функции в точке. Классификация точек разрыва. Свойства функ-

ции, непрерывной на замкнутом промежутке

163

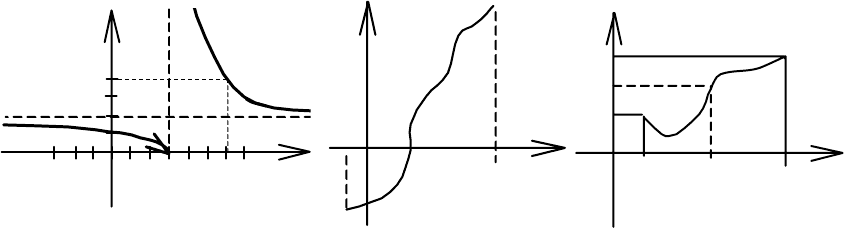
Теорема 4.26 (Больцано-Коши о нуле функции). Пусть функ-

ция f(x) непрерывна на замкнутом промежутке [a, b] и на концах это-

го промежутка принимает значения разных знаков. Тогда внутри

промежутка [a, b] найдётся по крайней мере одна точка с, в которой

функция f(x) обращается в нуль (рис. 4.31).

Эта теорема может быть использована для установления факта сущест-

вования корней уравнения f(x) = 0. Способа нахождения корней

она не даёт.

Ясно, что в условиях теоремы уравнение f(x) = 0 может иметь несколько

корней.

Теорема 4.27 (Больцано-Коши о промежуточном значении).

Пусть функция у = f(x) непрерывна на [a, b] и f(a)

≠

f(b). Тогда, каково

бы ни было число С

∈

[f(a), f(b)], внутри промежутка [a, b] найдётся

такая точка с, что f(c) = C. Или, что тоже самое, непрерывная на [a,

b] функция, переходя от одного своего значения f(a) к другому f(b),

принимает все промежуточные значения (рис. 4.32).

Рис. 4. 30

c b x

Рис. 4. 31

(

)

(

)

a c b x

Рис. 4. 32

Теорема 4.28 (Вейерштрасса об ограниченности функции)

Непрерывная на замкнутом промежутке функция ограничена на этом

промежутке.

Теорема 4.29 (Вейерштрасса о наибольшем и наименьшем

значениях).

Непрерывная на замкнутом промежутке функция прини-

мает на этом промежутке наибольшее и наименьшее значения.

Сформулированные здесь теоремы Больцано-Коши и теорема Вейер-

штрасса о наибольшем и наименьшем значениях относятся к так называе-

мым теоремам существования. Эти теоремы гарантируют существование

того или иного элемента, но не дают способа его нахождения.

4.9. Задачи для самостоятельного решения

. Вычислить пределы:

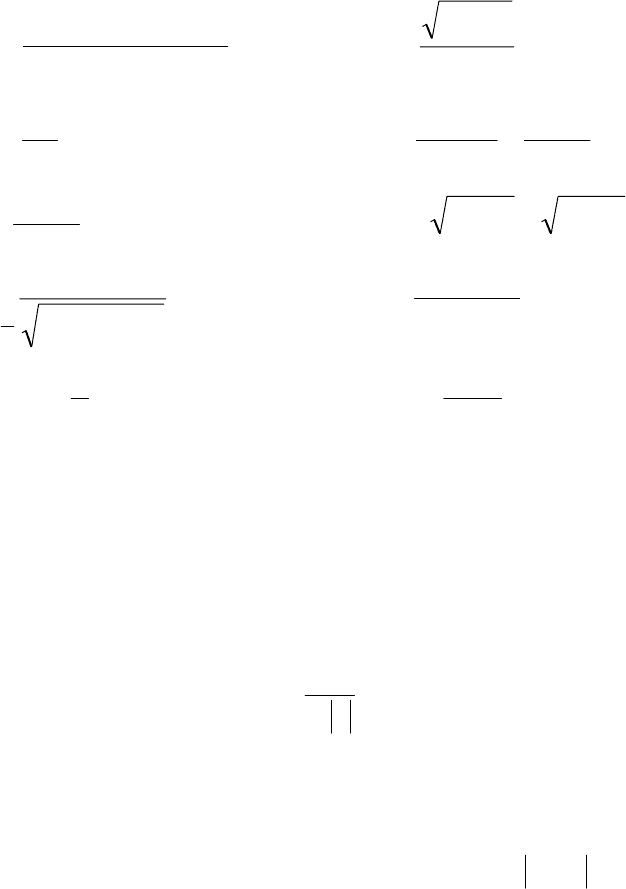
Глава 4. Введение в математический анализ

164

1.1.

()()

112

lim

−++

−−+

∞→

; 1.2.

lim

∞→

;

1.3.

()

++++

∞→

321

lim

; 1.4

⎟

⎠

⎞

⎜

⎝

⎛

−

∞→

lim

;

1.5.

3sin

lim

0→

; 1.6.

⎟

⎠

⎞

⎜

⎝

⎛

−−+

∞→

11lim

;

1.7.

()

sin1

cos

lim

−

→

; 1.8.

arcsin2

lim

0→

;

1.9.

⎟

⎠

⎞

⎜

⎝

⎛

∞→

1lim ; 1.10.

⎟

⎠

⎞

⎜

⎝

⎛

−

∞→

lim

2. При каком значении числа а будет непрерывной функция

()

⎪

⎩

⎪

⎨

⎧

>−

≤+

?1,3

,1,1

xax

3. Сколько точек разрыва (и какого рода) имеет функция

= ?

4.10. Вопросы для самоконтроля

В чём состоит геометрический смысл неравенства ε<− ax ?

Дайте определение предела числовой последовательности и его гео-

метрическую иллюстрацию.

Дайте определение и геометрическую иллюстрацию понятия предела

функции при

xx → .

Что означает запись

∞

→

)(lim

Сформулируйте теоремы о пределах (арифметические операции).

Сформулируйте основные свойства функции, непрерывной в точке и

на интервале.

Дайте классификацию точек разрыва и приведите их геометрическую

иллюстрацию.

приведите схему исследования функции на непрерывность.

Вопросы для самоконтроля

165

Когда при вычислении пределов используется второй замечательный

предел?

Запишите следствие из первого замечательного предела.

Дайте определение эквивалентных бесконечно малых.

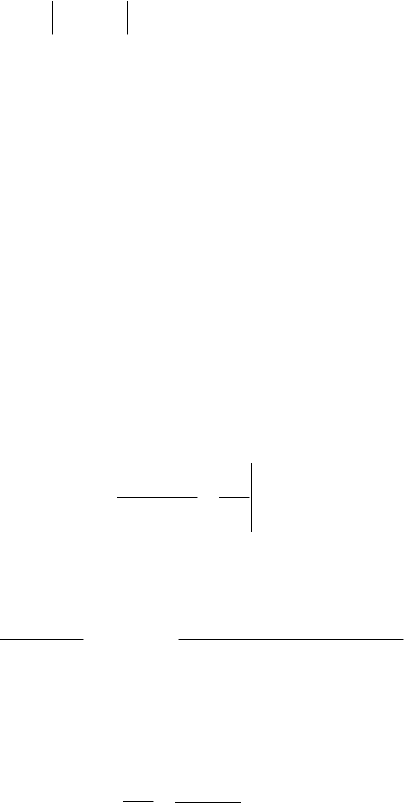
166

Глава 5. Дифференцирование функции одной перемен-

ной

5.1. Понятие производной. Механический и геометрический смысл

производной

Пусть функция у = f(x) определена в некоторой окрестности точки

т. е. на множестве

}:{)(

−

xxxxO

. Множество

)(

называется

δ-окрестностью точки

. Придадим фиксированному значению

прира-

щение Δх (положительное или отрицательное), такое, что

)(

xOxx

∈Δ+

Тогда приращение функции определяется выражением

)()()(

000

xfxxfxf

−

Δ . (5.1)

Определение 5.1. Производной функции у = f(x) в произвольной

фиксированной точке

x называется предел (если он существует и

конечен) отношения приращения функции к приращению аргумента

при условии, что последнее стремится к нулю.

Производная функции у = f(x) в точке

x обозначается следующим об-

разом:

)(

′

)(

′

xdf )(

Таким образом,

xfxxf

−

′

→Δ→Δ

)()(

lim

)(

lim)(

. (5.2)

Производная функции у = f(x) в произвольной точке х обозначается

так:

′

, )(xf

′

xdf

)(

При каждом конкретном числовом значении х производная (если она

существует при данном х) функции у = f(x) представляет собой определён-

ное число. При переменном значении х производная функции у = f(x) явля-

ется функцией аргумента х.

В дальнейшем под выражением «функция имеет производную» будем

понимать существование конечной производной.

5.1. Понятие производной

167

Определение 5.2. Если функция у = f(x) определена в левосто-

ронней окрестности точки

x и существует конечный или бесконеч-

ный предел этой функции

xfxxf

−

−→Δ

)()(

lim

, (5.3)

то он называется соответственно конечной или бесконечной

производной слева функции у = f(x) в точке

и обозначается так:

)0(

−

′

xf .

Определение 5.3. Если функция у = f(x) определена в правосто-

ронней окрестности точки

x и существует конечный или бесконеч-

ный предел этой функции

xfxxf

−

+→Δ

)()(

lim

, (5.4)

то он называется соответственно конечной или бесконечной

производной справа функции у = f(x) в точке

x и обозначается так:

)0(

′

xf .

Левую и правую производные называют односторонними производ-

ными.

Определение 5.4. Функция, определённая в некоторой окрест-

ности точки

x и имеющая в этой точке производную, называется

дифференцируемой в точке

x , причём

)0()0()(

000

′

−

′

xfxfxf

. (5.5)

Пример 1. Пользуясь определением, найти производную данной

функции (а – любое вещественное число):

1.1.

xy = ; 1.2. 56 −= xy ; 1.3.

y ln

Решение. Дадим аргументу х приращение Δх. Тогда и функция полу-

чит соответственное приращение Δу:

1.1.

()()()

(

)

⎥

⎦

⎤

⎢

⎣

⎡

−

+=−Δ+=−Δ+=Δ 11

xxxxxfxxfy .

Воспользовавшись таблицей эквивалентных бесконечно малых, полу-

чаем

Глава 5. Дифференцирование функции одной переменной

168

(

)

⋅=

−

⋅=

′

−

→Δ

−

→Δ→Δ

limlimlim

Итак,

(

)

1−

⋅=

′

xax .

1.2.

(

)

(

)

−−−Δ+

′

→Δ→Δ

5656

limlim

xxx

(

)

(

)

()

−+−Δ+Δ

−

→Δ

5656

lim

xxxx

xxx

()

−+−Δ+Δ

→Δ

5656

lim

xxxx

−x

1.3.

()

(

)

xxxy

=−Δ+=Δ 1lnlnlnln ;

(

)

(

)

()

′

∞

→Δ→Δ→Δ

11lnlim

1ln

limlim

000

xxx

(

)

ln1limln

⎟

⎠

⎞

⎜

⎝

⎛

→Δ

(см. [1] (второй замечательный предел)).

Итак,

()

ln =

′

Пример 2. Исходя из определения производной, найти )0(f

′

2.1.

⎪

⎩

⎪

⎨

⎧

≠

⎟

⎠

⎞

⎜

⎝

⎛

0;0,

;0,

sintg

)(

2.2.

⎪

⎩

⎪

⎨

⎧

≠

⎟

⎠

⎞

⎜

⎝

⎛

0;0,

;0,

cosarctg

)(

2.3.

⎪

⎩

⎪

⎨

⎧

≠−

0.0,

;0,cos

)(

xxe

5.1. Понятие производной

169

Решение. Дадим аргументу х = 0 приращение Δх. Тогда функция по-

лучит соответствующее приращение Δу.

2.1.

−

−Δ+=Δ )0()()()(

sin)()(tg

−

⎥

⎦

⎤

⎢

⎣

⎡

⋅Δ+Δ=

⎥

⎦

⎤

⎢

⎣

⎡

⋅Δ+Δ=

sin)()(tg

Найдём по определению

)0(y

′

⎥

⎦

⎤

⎢

⎣

⎡

⋅Δ+Δ

′

→Δ→Δ

sin)()(tg

limlim)0(

⋅Δ+Δ

→Δ

sin)()(

lim

⎟

⎠

⎞

⎜

⎝

⎛

⋅Δ+Δ=

→Δ→Δ

sinlim)(lim

sinlim0

⎟

⎠

⎞

⎜

⎝

⎛

⋅Δ+=

→Δ

т. к. произведение бесконечно малой на ограниченную функцию есть

величина бесконечно малая.

Итак, )0(y

′

= 0.

2.2.

=−

⎟

⎠

⎞

⎜

⎝

⎛

Δ=−Δ=−Δ+=Δ 0

cosarctg)0()()()(

xfxfxfxxfy

⎟

⎠

⎞

⎜

⎝

⎛

Δ=

cosarctg .

По формуле (5.2) имеем

⎥

⎦

⎤

⎢

⎣

⎡

⋅Δ

′

→Δ→Δ

cosarctg

limlim)0(

⋅Δ

→Δ→Δ

coslim

cos

lim

Таким образом, производная функции в точке х = 0 не существует, т. к.

→Δ

coslim

не существует.

2.3.

−

−Δ+=Δ )0()()()(

Глава 5. Дифференцирование функции одной переменной

170

xexe

Δ−=−Δ−=

ΔΔ

cos0cos

)()(

По определению проверим, существует ли в точке х = 0 производная

данной функции:

Δ−+

⎟

⎠

⎞

⎜

⎝

⎛

−

Δ−

′

→Δ

→Δ→Δ

)cos1(1

lim

cos

limlim)0(

)(

0lim

)(

lim

=Δ=

+Δ

→Δ→Δ

Следовательно,

0)0( =

′

y .

При вычислении предела применили таблицу эквивалентных беско-

нечно малых:

)(

−

Δx

e ∼

)( xΔ при Δх → 0;

1 – cosΔx ∼

)(

xΔ

при Δх → 0.

5.1.1. Механический смысл производной

Рассмотрим функцию у = f(x), определённую и непрерывную в некото-

рой окрестности точки

x . Придавая аргументу

x приращение Δх (поло-

жительное или отрицательное), такое, что )(

xOxx

∈

, получим соот-

ветствующее приращение функции

)()()(

xfxxfxf

−

Δ .

Тогда средняя скорость изменения функции определяется следующим

соотношением:

)(

ср.

Выполняя предельный переход при Δх → 0, получим мгновенную ско-

рость изменения функции

)(

lim

′

→Δ