Аракелян А.К., Афанасьев А.А. Вентильные электрические машины и регулируемый электропривод. Книга 1

Подождите немного. Документ загружается.

Вычисление магнитного потока взаимоиндукции не тре-

бует, вообще говоря, знания вектора магнитной индукции —

достаточно ограничиться нахождением его радиальной со-

ставляющей.

Локальная магнитная проводимость, рассчитанная для

конкретно выбранной окружности и являющаяся функций

одной линейной (угловой) координаты, после умножения на

МДС обмоток дает радиальную составляющую индукции в

точках указанной окружности ВЗ. В принципе изменение

этой составляющей индукции по высоте ВЗ может быть уч-

тено соответствующим изменением локальной магнитной

проводимости. На значение индукции в ВЗ влияют не только

геометрия пазов и значения токов в них, но и характер рас-

пределения проводников в пазах. Для полного исключения

этого последнего влияния, т.е. для однозначного определе-

ния МДС обмоток, необходимо допустить, что проводники

расположены бесконечно тонким слоем на дне пазов (глуби-

на погружения проводников равна высоте паза) .

В практике инженерных расчетов можно считать, что

указанный эффект достигается при глубине погружения

проводников в паз на величину не менее половины его от-

крытия [150]. (Для открытых пазов с любым значением от-

ношения ширины паза

к размеру воздушного зазора

 ( )0   

имеем

h b

 0 6, ). Таким образом, при из-

вестных значениях одномерной функции МДС и, в общем

случае, двухмерной функции магнитной проводимости нахо-

дится распределение индукции на выбранной линии (в част-

ности, одномерной) ВЗ.

Расчет такого распределения существенно облегчается тем,

что, как свидетельствует опыт, магнитная проводимость для

средней окружности ВЗ может считаться равной, в первом при-

ближении, произведению частичных магнитных проводимостей,

полученных аналитически для односторонней зубчатости ВЗ

[93]. Очевидно, что при обеспечении достаточно низкой мето-

дической погрешности, этот метод позволит получить сравни-

тельно надежные результаты электромагнитного расчета уста-

новившегося и переходного режима при допустимых в инже-

нерной практике вычислительных затратах.

Целесообразно на основе конформного отображения оце-

нить погрешность метода магнитной проводимости и обос-

новать пути повышения точности расчета МП указанным

методом.

1.2. Расчет постоянных конформного преобразования

Конформные отображения полуплоскости на внутрен-

ность линейных многоугольных областей, основанные на

дифференциальном уравнении Кристоффеля-Шварца, явля-

ются эффективным средством для исследования плоскопа-

раллельных векторных полей [192]. В частности, с их помо-

щью возможен как аналитический, так и численный расчет

характеристик магнитного поля в воздушном зазоре и пазах

(в том числе занятых проводниками с током) электрических

машин [125]. При практическом использовании дифферен-

циального уравнения Кристоффеля-Шварца

C t a

 









( )

1

, (1.1)

где

Ñ a j n

, ( , , )



1 2  — некоторые постоянные, причем

числам

на вещественной оси плоскости

соответству-

ют вершины многоугольника с внутренними углами  

(общее число его вершин

), заданного в плоскости z;





, если все числа

ограниченные;







, если одно из чисел

(например,

) равно

бесконечности,

его постоянные должны быть известными.

К сожалению непосредственный аналитический расчет

этих постоянных возможен только для многоугольников со

сравнительно небольшим числом вершин и, следовательно,

простой конфигурации [175, 193]. Для областей, которые

ближе всего соответствует реальным техническим приложе-

ниям, постоянные могут находиться численными методами

[6].

Ниже рассматривается метод расчета постоянных, осно-

ванный на дифференциальном продолжении решения по па-

раметру [119] и регуляризации особых точек при интегриро-

вании уравнения (1.1) методом Л. В. Канторовича [165, 258].

1.2.1. Общие особенности расчета постоянных

Допустим дифференциальное уравнение (1.1) реализует

однозначное соответствие точек верхней полуплоскости

—

угольной области

. Как известно, из

постоянных три

могут выбираться произвольно (целесообразно одну из них

принять равной бесконечности). Следовательно, уравнение

(1.1) может быть соотнесено с конкретным многоугольни-

ком, если будут определены (

2) неизвестных: это (

3) по-

стоянных

и комплексный коэффициент

. Аргумент по-

следнего легко находим по уравнению (1.1) [174], взяв ка-

кую-либо точку 

на оси абсцисс плоскости

, например,

a a

1 2

  . Этой точке будет соответствовать некоторая точ-

ка

на стороне

многоугольника, аргумент которой

(arg

) известен. Если приращение

от точки 

взять в

направлении оси абсцисс (arg

dt =

0 ), то: arg

dz =

arg

Тогда из уравнения (1.1) следует:

arg arg ( )

C z

m j

  







 

. (1.2)

Отметим, что (

2) неизвестным соответствуют (



) сто-

роны многоугольника с заданными длинами

(

=1,2,...,

2), которые связаны с уравнением (1.1) зависимо-

стями

При наличии у многоугольника вершин, расположенных в беско-

нечности, в систему (1.3) включаются уравнения, фиксирующие

конечные разности двух бесконечных длин сторон, примыкающих к

таким вершинам.

C t dt l

( )







, (1.3)

где





( ) ( )

t t a

 







. (1.4)

Таким образом, для определения (

2) неизвестных

(

, a

r2,...,

r(n



) и

— необходимо решить (

2) нелинейных

уравнения вида (1.3)

Введем обозначения:

x f l

; ; — векторы-столбцы разме-

ром (

2), причем:









 

 

x x x a a a C

n r r r n

1 2 2 1 2 3

 

( )

;









f l

T T

 

 

f f f l l l

n n

1 2 2 1 2 2

 ; ,

где

f x t dt k n

k n

  







1 2 2

( ) , ( , , , )

. (1.5)

Система уравнений (1.3) запишется в виде:

f l

  0 . (1.6)

Найдем ее решение методом дифференциального про-

должения решения по параметру . С этой целью представим

(1.6) в такой форме:

l f



 

 

 , (1.7)

Могут быть произвольными вместо трех постоянных

две из них и ко-

эффициент

где



— вещественный параметр с областью непрерывного

изменения

0  

; (1.8)

— вектор-столбец, элементы которого находятся по

формуле (1.5) для некоторого произвольного значения

вектора

x x



Уравнение (1.7) задает систему неявных функций:

x x k n

k k

  ( ) ; , , , 1 2 2 , (1.9)

непрерывно зависящих от параметра



, причем решение

x x



соответствует значению параметра

  0

, т. е.

x x

0 ( ) . При

 

уравнение (1.7) принимает вид (1.6),

следовательно, решение

x x Ò

k k

 ( ) является искомым. Со-

гласно теории неявных функций, решение (1.7) единственно,

если определитель матрицы Якоби этого уравнения





(1.10)

отличен от нуля.

Дифференцируя векторное уравнение (1.7) по параметру



, получим обыкновенное дифференциальное уравнение по-

рядка (

n—





W x l f



 



, (1.11)

где



x x



d d

 — вектор-столбец производных искомых

переменных по параметру



Численное интегрирование уравнения (1.11) при соблю-

дении условия

 0

может производиться стандартными методами математиче-

ского обеспечения ЭВМ, например, методом Рунге-Кутта

того или иного порядка. Опыт показывает, что в ряде случа-

ев целесообразно производить это интегрирование грубо (со

сравнительно большой погрешностью), но в

опорных точ-

ках интервала (1.8)



jT m j m

 , , ,1 2 

уточнять решения (1.9) до необходимой точности итераци-

онным методом Ньютона:

W Q

j j j

p p p

   , (1.12)

где





Q f l f f

   



 ;

— номер итерации в

точке





 

интервала (1.8) ;

W f

; — матрица Якоби и векторная функция

, най-

денные для значений

x x



, взятых при  

;



— вектор невязки для

-ой итерации.

Количество опорных точек

на интервале (1.8) выбира-

ется достаточно малым из условия, чтобы в каждой из них

итерационный процесс был сходящимся. В большинстве слу-

чаев целесообразно уравнение (1.11) интегрировать методом

Эйлера и проводить процедуру Ньютона на каждом шаге ин-

тегрирования, причем величина шага диктуется устойчиво-

стью этой процедуры. В ряде случаев счет оказывается более

производительным, когда движение по



в уравнении (1.7)

совершается только в соответствии с одним итерационным

методом Ньютона (используется формула (1.12); интегриро-

вание уравнения (1.11) не производится).

Выбор размера интервала (1.8) не имеет принципиально-

го значения. Пропорционально ему выявляется из опыта не-

обходимый шаг движения по параметру



. При отсутствии

специфических требований к этому параметру целесообраз-

нее принять

= 1.

Начальные значения переменных

в общем случае, при

отсутствии оценочных сведений об области их существова-

ния, выбираются произвольно с единственными ограниче-

ниями:

a x

1 1

 ;

x x

j j



1

Следует также привести знаки переменных в соответст-

вие с выбранным расположением начала координат ком-

плексной плоскости. Возможный диапазон изменения пере-

менных от начального значения при

  0

до искомого ре-

шения при

 

иллюстрирует приведенный в конце этого

раздела пример.

1.2.2. Постоянные немагнитного зазора с прямоугольными

пазами конечной и бесконечной глубины

Для некоторых незамкнутых многоугольников с нулевы-

ми внутренними углами модуль коэффициента

может быть

определен по простой формуле:







, (1.13)

где 

— немагнитный (воздушный) зазор у открытой вер-

шины, соответствующей постоянной

  на вещест-

венной оси плоскости

Это будут многоугольники, для которых уравнение Кри-

стоффеля-Шварца представляется в виде:

t a







 





( )



, (1.14)

причем

а)

( ) ( ) 

r sk

1 1   





;

б) одна из открытых вершин соответствует началу коор-

динат плоскости

Рис. 1.1. Конформное отображение открытой области с пазами ко-

нечной глубины

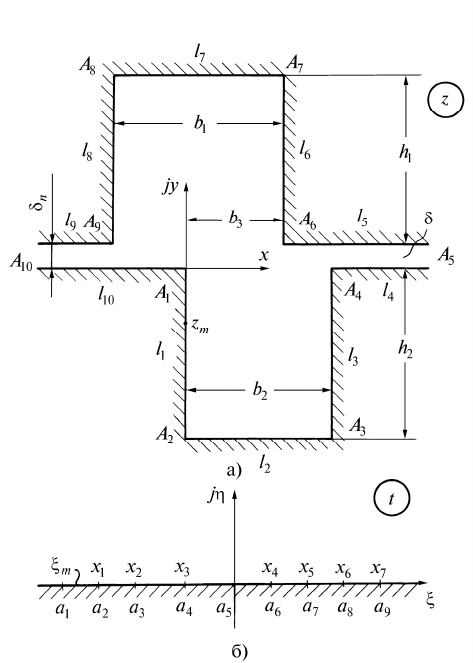
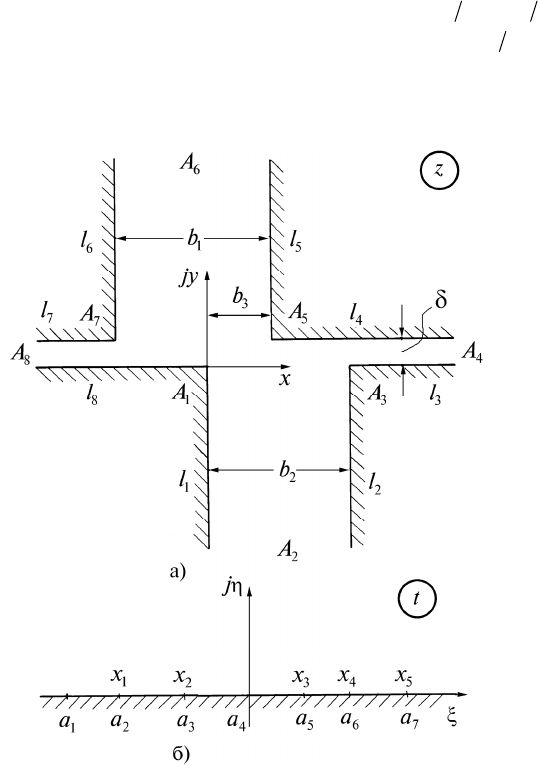
К ним, например, можно отнести многоугольники, со-

держащие: 1) одинаковое число вершин с углами  2 и 3 2

(рис.1.1, а), 2) вдвое большее число вершин с углами 3 2 по

сравнению с числом открытых вершин бесконечно глубоких

пазов (рис. 1.2, а). В справедливости формулы (1.13) легко

убедиться, приняв для окрестности точки

  выражение

Рис. 1.2. Конформное отображение открытой области с пазами бес-

конечной глубины

t R e R

  



, ( ) . (1.15)

Причем очевидно:

dt jt d

  . (1.16)

Тогда из формулы (1.14) после подстановки в нее выражений

(1.15), (1.16) следует при

 

dz jC d

  .

Интегрируя это выражение по верхней дуге плоскости

бесконечно большим радиусом и учитывая величины изме-

нения



( соответственно



и 

 ) , получим формулу

(1.13).

Для десятиугольной области (

= 10) на рис 1.1 примем:

a a a

1 5 10

10 0    ; ; ;









 

x x x a a a a a a a

1 2 7 2 3 4

7 8 9

 .

Поскольку

 9, по формулам (1.2), (1.13), (1.4) найдем:

t a t x t x t x

t x t x t x t x

 



   











 



;

( )

( )( )( )( )

1 3 4 7

1 2 5

(1.17)

Первые пять уравнений системы (1.6) соответствуют дли-

нам трех сторон нижнего паза (рис. 1.1, а) (

l h l b

1 2 2 2

 ; ;

l h

3 2

 ) и — двух сторон верхнего паза (

;

Шестому уравнению отвечает разность бесконечных длин

сторон многоугольника

(

—

). С целью

уменьшения количества интегралов в исходной системе (1.6)

в качестве седьмого уравнения используем результат интег-

рирования уравнения (1.1) в окрестностях точек

0 ;