Антонюк А.О. Теоретичні основи захисту інформації
Подождите немного. Документ загружается.

151
• r∈(execute, append);
• r∈(read, write) і
)()( ofsf
os
≥
.
Означення. Стан v=(b,М,f,h)∈V володіє ss-властивістю, якщо кожний
елемент (s,o,x)∈b володіє ss-властивістю відносно f.
Означення. Доступ (s,o,r)∈S×O×R задовольняє *-властивості, (властивість
«зірка») відносно
Ffffff
cs
∈= ),,,(
0
, якщо викону єть ся од н а з ум о в :
• r=execute;
• r=append і
)()( sfof
co
>
;
• r=read і
)()( ofsf
oc
>
;
• r=write і
)()( ofsf
oc
=
.
Означення. Стан v=(b,М,f,h)∈V володіє *-властивістю, якщо кожний
елемент (s,o,r)∈b володіє *-властивістю відносно f.
Означення. Стан v=(b,М,f,h)∈V володіє *-властивістю, щодо підмножини
суб'єктів S', S'⊆S, якщо кожний елемент (s,o,r)∈b, де s∈ S', володіє *-
властивістю відносно f. При цьому множина S\S' називається множиною
довірених суб’єктів, тобто суб’єктів, що мають право порушувати правила
політики безпеки.
Означення. Стан системи v=(b,М,f,h)∈V володіє ds-властивістю, якщо для
кожного елемента (s,o,r)∈b виконується r∈M
so
.
Означення. Стан системи v=(b,М,f,h)∈V називається безпечним, якщо він
володіє одночасно ss-властивістю, *-властивістю відносно S' і ds-властивістю.
Ось деякі коментарі щодо наведених властивостей безпеки системи.
Нагадаємо, що формулювання політики MLS пов'язане з решіткою
цінностей SC×L, де L – лінійний порядок, SC – решітка підмножин в інформації
наступним чином: інформаційний потік між двома об'єктами називається
дозволеним, якщо клас об'єкта-джерела домінується класом об'єкта-
одержувача.

152
Покажемо, зокрема, чому саме в моделі Б-Л для опису відношення
домінування на множині рівнів безпеки використовується решітка.
Якщо інформація може передаватися від сутностей класу А до сутностей
класу В, а також від сутностей класу В до сутностей класу А, то класи А і В
містять однорівневу інформацію і з точки зору безпеки є еквивалентними
одному класу (АВ). Т ому для видалення надлишкових класів необхідно, щоб
відношення ≤ було антисиметричним.
Якщо інформація може передаватися від сутностей класу А до сутностей
класу В, а також від сутностей класу В до сутностей класу С, то очевидно, що
вона буде також передаватися від сутностей класу А до сутностей класу С.
Таким чином, відношення ≤ повинно бути транзитивним.
Так як клас сутності визначає рівень безпеки інформації, що міститься в
ньому, то всі сутності одного й того ж класу містять з точки зору безпеки
однакову інформацію. Отже, немає сенсу забороняти потоки інформації між
сутностями одного й того ж класу. Більше того, з чисто практичн их міркуван ь
слід надавати можлив ість для сутності передавати інформ ації самій собі. Отже,
відношення ≤ повинно бути рефлексивним.
Тепер залишається показати, що для будь-якої множини сутностей повинні
існувати єдина найменш а верх ня і єдина найбільш а ниж н я гран иц і множин
відповідних ним рівнів безпеки. Для пари сутностей х і у, що володію ть рівнями
безпеки а і b відповідно, позначимо найбільший рівень безпеки їх комбінації як
(а
⊕
b), при цьому а≤(а
⊕
b) і b≤(a
⊕
b). Тоді, якщо існує деякий рівень с таки й,
що а≤с і b≤с, то по ви н н о мати місце відн о ш е нн я (а
⊕
b) ≤с, оскіл ьк и (а
⊕
b) – це
мінімальний рівень суб’єкта, для якого доступна інформація як з х, так і з у.
Отже, (a
⊕
b) повинно бути найменшею верхньою границею а і b. Аналогічн о
позначимо найменший рівень безпеки комбінації сутностей х і у як (а
⊗
b), при
цьому (а
⊗
b)≤а і (a
⊗
b)≤b. Тод і, якщо існує деяки й рівень с такий, що с≤а і с≤b,
то п овинно мати місце відношенн я с≤(а
⊗
b), оскільки (а
⊗
b) – це максимальний
рівень суб’єкта, для якого дозволена передача інформації як в х, так і в у. Отже,
(a
⊗
b) повинно бути найбільшею нижньою границею а і b.

153
Використання решітки для опису відношень між рівнями безпеки дозволяє
застосовувати в якості атрибутів безпеки (елементів множини L) не тіль ки цілі
числа, для яких визначено відношення «меньше або дорівнює», але й більш
складні елементи. Наприклад, в державних організаціях досить часто в якості
атрибутів безпеки використовують комбінацію, що складається з рівня безпеки
– цілого числа, і набору категорій з деякої множини. Такі атрибути неможливо
порівнювати за допомогою арифметичних операцій, отже, відношення
домінування ≤ визначається як композиція відношення «меньше або дорівнює»
для рівнів безпеки і відношення включення множин для наборів категорій.
Причому це ажніяк не впливає на властивості моделі, оскільки відношення
«меньше або дорівнює» і «вкл ючен ня множин» мають властивості
антисиметричності, транзитивності і рефлексивності, а, отже, їх ком пози ція
також буде володіти ц іми властивостями, створюючи над множиною атрибутів
безпеки решітку. Т аким же чином можна використовувати будь-які види
атрибутів і будь-яке відношення часткового порядку, аби їх сукупність
представляла собою решітку.
Далі, як неважко помітити, з означення ss-властивості випливає, що в
безпечному стані можливе читання (read) тільки вниз, що погодж ує тьс я з
еквівалентним визначенням MLS політики. Крім того, ss-властивість визначає
обмеження на можливість модифікації, яка пов'язана з доступом write, я кщо
)()( ofsf
os
<
. Таким чи н о м, функція
)(sf
s
визначає для суб’єкта s верхній
рівень таємності об’єктів, до яких він потенційно може отримати доступи read
або write.
З володіння доступом *-властивості відносно f випливає володіння цім
доступом ss-властивості відносно f. Т ак и й висновок л ег ко отримати, зв а ж аю ч и ,
що
)()( sfsf
cs
>
.
В чому суть *-властивості? Якщо суб'єкт s може понизити свій поточний
допуск до
)()( ofsf
oc
=
, то, згідно *-властивості, він може отримати доступ
write до об'єкту о, але не доступ read до об’єкту о' з рівнем
)()( sfof
co
>
!
.
154
Хоча при цьому, можливо, виконується
)()( ofsf
os
!
=
, і в я ки х о сь інших
станах системи суб’єкт s може отримати доступ read до об’єкту о'. Таким
чином, *-властивість виключає появу в системі каналу витоку зверху донизу, як
це і відповідає мандатній політиці безпеки.
Щоб довести, що будь-який інформаційний потік на траєкторії системи
дозволений, достатньо показати, що, виходячи з безпечного стану і слідуючи
допустимим діям, знову приходимо в безпечний стан. Тобто тоді будь-яка
реалізація системи буде безпечною. Проте перевірка безпеки системи за
означенням в більшості випадків не може бути реалізованою в зв’язку з тим, що
при цьому необхідна перевірка усіх реалізацій системи, а їх безкінечно багато.
Значить, необхідно визначити і обґрунтувати інші умови безпеки системи, які
можна було б перевіряти на практиці.
Означення. Реалізація (х, у, z) системи ∑(Q, D, W, z) волод іє ss-
властивістю (*-властивістю, ds-властивістю), якщо в послідовності станів
(z
0
,z
1
,.....) кожен стан z
n
має ss-властивість (*-властивість, ds-властивість).
Означення. Система володіє ss-властивістю (відповідно, *-властивістю,
ds-властивістю), якщо кожна її реалізація володіє ss-властивістю (відповідн о, *-
властивістю, ds-властивістю).
Означення. Система називається безпечною, якщо вона володіє одночасно
ss-властивістю, *-властивістю і ds-властивістю.
Тепер можна сформулювати ряд основних тверджень моделі.
Теорема А1. Система ∑(Q, D, W, z
0
) володіє ss-властивістю для будь-якого
початкового стану z
0
, що має ss-властивість тоді і тільки тоді, коли множина дій
системи W задовольняє наступним умовам для кожної дії (q, d, (b*, М*, f*, h*),
(b, М, f, h))∈ W:
Умова 1. ∀(s,o,r)∈b*\b володіє ss-властивістю відносно f*.
Умова 2. Якщо (s,o,r)∈b і не володіє ss-властивістю відносно f*, то
(s,o,r)∉ b*.

155
Теорема А2. Система ∑ (Q, D, W, z
0
) володіє *-властивістю відносно S' для
будь-якого початкового стану z
0
, що володіє *-властивістю відносно S' тоді і
тільки тоді, к о ли множи н а дій системи W задово льняє наступним умовам для
кожної дії (q, d, (b*, М*, f*, h*), (b, М, f, h))∈W:
Умова 1. ∀S∈S’, ∀(s,o,r)∈ b*\b володіє *-властивістю відносно f*.
Умова 2. ∀S∈S’, якщо (s,o,r)∈ b і не володіє *-властивістю відносно f*, то
(s,o,r)∉ b*.
Теорема АЗ. Система ∑(Q, D, W, z
0
) володіє ds-властивістю тоді і тільки
тоді, коли для будь-якого початкового стану z
0
,, що в ол о д іє ds-властивістю
множина дій системи W задовольняє н аступн им умовам для будь-якої дії (q, d,
(b*, М*, f*, h*), (b, М, f, h))∈W:
Умова 1. Для ∀(s,o,r)∈b*\b виконується r∈M
so
.
Умова 2. Якщо (s,o,r)∈b і r∉M
so
, то (s,o,r)∉b*.
Теорема BST (Basic Security Theorem). Система ∑(Q, D, W, z
0
) безпечна
тоді і тільки тоді, коли z
0
– безпечний стан і множина дій системи W
задовольняє умовам теорем А1, А2, А3.
Описана вище класична модель Б-Л пропонує загальний підхід до
побудови систем, що реалізують мандатну політику
безпеки. В моделі Б-Л
визначається, якими властивостями повинні володіти стани і дії системи, щоб
вона була безпечною відповідно
до наданого озн ачення. В той же час в моделі
не вказується конкретно, що повинна робити система за запитами на доступ
суб’єктів до об’єктів при переході зі стану в стан, як конкретно повинні при
цьому змінюватися значения елементів моделі, тобто має місце певна
невизначеність щодо прийняття конкретних рішень.
Приклад. Нехай суб’єкт S запитує доступ read до об’єкту О. Реалізувати
це система може одним з наступних шляхів:
1) заборонити суб’єкту S доступ read до об’єкту О;

156
2) закрити доступ write суб’єкта S до об’єкта О , підв ищити поточний
рівень таємності f
c
(s) до High, до з во л и ти суб’єкту S доступ read до об’єкту О,
який він запитує.
Як бачимо, кожен з описаних шляхів відповідає вимогам безпеки моделі
БЛ.
В реальних системах можливі більш складні ситуації, ніж ситуація з
даного прикладу. Крім того, можливо використання в системі інших видів
доступу суб’єктів до об’єктів, які вимагатимуть довизначення властивостей
безпеки, що не завжди легко зробити. В зв’язку з цім велике значення має
коректне визначення властивостей безпеки.
Більше того, запропоновано конкретний приклад, де замість *-властивості
використана абсурдна з точки зору здорового глузду властивість [83-85]. Однак
при цьому не виникає жодних протиріч в логиці доказу теорем, що визначають
умови безпеки системи.
Припустимо, що інший набір властивостей було обрано для визначення
концепції безпечного стану. Якщо BST справді є підставою для впевненості в
тому, що модель Б-Л дійсно здатна підтримати потрібний рівень безпеки, то не
повинно бути можливості довести таку саму теорему для моделі безпеки, в якій
безпечний стан визначено абсолютно іншим чином. Також, неможливою має
бути ситуація, коли теорема мож е бути доведена для системи, що очевидно не є
безпечною.
Отже, визначимо †-властивість наступним чином: ∀ (s,o,w)∈b,
)()( ofsf
oc
>
.
Власне кажучи, це є протилежність *-властивості, та дозволяє суб’єктам
передавати інформацію з вищих рівнів безпеки до ниж чих. Отже, ця модель не
є безпечною, оскільки вона дозволяє копіювати таємну інформацію в
некласифіковані файли. Визначимо тепер безпечний стан як такий, що
відповідає ss-властивості, †-властивості та ds-властивості. За Беллом та
ЛаПадулою теорема BST може бути доведена як висновок доведення наступних
трьох теорем.

157
Теорема А1*. Система ∑(Q, D, W, z
0
) володіє ss-властивістю для будь-
якого початкового стану z
0
, що має ss-властивість тоді і тільки тоді, коли
множина дій системи W задовольняє наступним умовам для кожної дії (q, d, (b*,
М*, f*, h*), (b, М, f, h))∈W:
Умова 1. ∀(s,o,х)∈b*\b володіє ss-властивістю відносно f*.
Умова 2. Якщо (s,o,х)∈b і не воло д іє ss-властивістю відносно f*, то
(s,o,х)∉ b*.
Теорема А2*. Система ∑(Q, D, W, z
0
) володіє †-властивістю відносно S'
для будь-якого початкового стану z
0
, що володіє †-властивістю відносно S' тоді
і тільки тоді, коли множ ина дій системи W задовольняє наступн им умовам для
кожної дії (q, d, (b*, М*, f*, h*), (b, М, f, h))∈W:
Умова 1. ∀S∈S’, ∀(s,o,х)∈ b*\b володіє †-властивістю відносно f*.
Умова 2. ∀S∈S’, якщо (s,o,х)∈b і не во л о діє †-властивістю відносно f*, то
(s,o,х)∉ b*.
Теорема АЗ*. Система ∑(Q, D, W, z
0
) волод іє ds-властивістю тоді і тільки
тоді, коли для будь-якого початкового стану z
0
,, що в ол о д іє ds-властивістю
множина дій системи W задовольняє н аступн им умовам для будь-якої дії (q, d,
(b*, М*, f*, h*), (b, М, f, h))∈W:
Умова 1. Для ∀(s,o,х)∈b*\b виконується х∈M
so
.
Умова 2. Якщо (s,o,х)∈b і r∉M
so
, то (s,o,х)∉b*.
Теорема BST*. Система ∑(Q, D, W, z
0
) безпечна тоді і тіль ки тоді, коли z
0
–
безпечний стан і множина дій систем и W задовольняє умовам теорем А1*, А 2*,
А3*.
Отже, ми довели, що BST насправді не доводить, що система дійсно є
безпечною.
Існують і інші підходи залежно від умов практичного застосування моделі
або з метою подальшого її дослідження. Аналогічною є ситуація для кожного
визначення «безпечного стану» в системі, чиї стани можуть бути

158
проіндексовані для підтримки індукції. В такому разі, це є властивість
індексації станів, а н е б ез пе ки .
Може здатися, що BST є важливим інструментом, що дозволяє доводити
безпечність кожного досяжного стану системи тільки за рахунок розгляду
початкового стану та правил, що переводять систему з одного стану до іншого.
Теорема стверджує, що якщо система стартує з безпечного стану, та всі її
перетворення є такими, що в кожному стані забороняється будь-який старий
доступ, що порушує безпеку згідно з правилами визн ачення нового стану, та не
створюються нові доступи , що порушують безпеку, то система залишатиметься
безпечною. Проте, це є настільки ж очевидним, настільки і марним. Коротше,
теорема не стосується реальних проблем.
Залежно від умов практичного застосування моделі або в цілях її
подальшого дослідження можливно використання еквівалентних підходів щодо
визначення властивостей безпеки.
Отже, хоча модель Б-Л є базовою моделлю безпеки, яка складає основу
теорії захисту інформації, однак її застосування на практиці пов’язано з
великими труднощами.. Тому в реальному житті вона використовується лише в
системах, де обробляється класифікована інформацію і застосовується л ише
для обмеженої підмножини суб’єктів і об’єктів.
В той же час модель Б-Л породила цілий напрямок в теорії захисту
інформації. Озна чен н я та вл а ст ив о ст і дан о ї мод ел і доз в о ля ю ть забе зп еч у ва ти
конфіденційність інформац ії в системі. На базі моделі Б-Л було сформульовано
політику цілісності Біба [86-87], ціллю якої є забезпечення цілісності даних, та
отримано цілу низку інших важливих теоретичних і практичних результатів.
159
РОЗДІЛ 6. ЗАГАЛ ЬНІ М О Д ЕЛІ
Нижче розглядаються моделі загального типу, в яких основним є не
питання доступу суб’єктів до об’єктів, а інші аспекти без п еки . Зокрема, завжди
виникають питання вартості захисту інформації, організації процесу захисту,
моделювання самої системи захисту і багато інших. Звичайно, ці різні асп ект и
захисту інформації для свого моделювання вимагають і різних підходів, різних
математичних апаратів, різної інтерпретації моделей. Тому кожну з
розглянутих нижче моделей фактично можна вважати черговим формальним
методом дослідження питань інформаційної безпеки. Слід однак зазначити, що
розглядаються лише найбільш розповсюджені і популярні математичні моделі.
6.1. Модель про ц есу з ах и ст у
Прикладом застосування загальних моделей захисту може бути модель
процесу захисту [39]. У самому загальному виді про ц ес захи с ту інф ор м ац ії
можна представити в наступному вигляді.
Вважатимемо, що обробк а інфо р ма ц ії на об’єктах систем и здісню є тьс я в
умовах дії на інформацію загроз (або дестабілізуючих факторів – ДФ). Для
протидії загрозам інформації можуть використовуватися спеціальні засоби
захисту, які здійснюють нейтралізуючу дію на ДФ. Нехай
i
O
– і-ий об’єкт
захисту, стан якого може змінюватися за часо м,
j
T
– дестабілізуючий фактор,
l
C
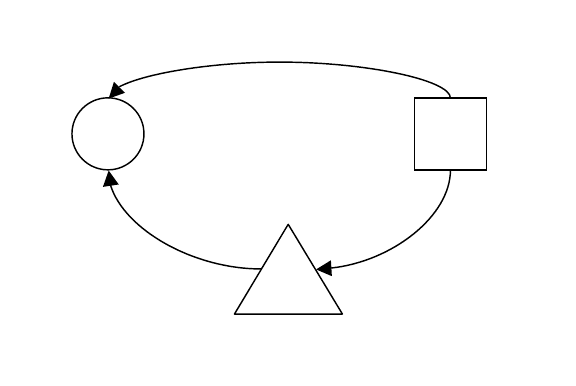
– засіб захисту. То ді процес захисту інформації можна представити у
вигляді наступної схеми. Система може знаходитися в різних станах, що
підкреслюється індексом k.
O
i
T
j
C
l
P
ijk
Загроза
P
ijkl
Засіб захисту
Об’єкт

160
Тоді, якщо
ik
P
є ймовірністю захищеності і-го об’єкта в k-му стані і ці
ймовірності є незалежними, то
∏
∀
−−=
k
kiki
PP
α
)1(1
,
де
k
α
– доля k-го стану (режиму роботи) ІТС за період часу, що
аналізується. Цю долю найбільш об’єктивно можна оцінити , в важаю чи
представлення
k
α
у вигляді долі інтервалу часу ІТС в k-му стані (
k
tΔ
) в
загальній тривалості часу, який оцінюється величиною
TΔ
, тобто
T
t
k
k
Δ
Δ
=
α
.
Для загального випадку, звичайно, слід вважати, що СЗІ може бути
неповною в тому сенсі, що в ній можуть бути відсутніми засоби попередження
деяких ДФ. Тоді
ikikik
PPP
!!!
=
,
де
ik
P
!
– ймовірність захищеності інформації на і-ому об’єкті в k-му його
стані (режимі роботи) від сукупної дії від тих ДФ, для протидії яким в системі
захисту не передбачені засоби захисту;
ik
P
!!
– те ж для ДФ , протидія яким
можлива на основі засобів захисту, що присутні в системі захисту.
В свою чергу
∏
∀
−=
$
j
ikjik
PP )1(
,
де j приймає значення номерів тих ДФ , проти яких відсутні засоби захисту,
ikj
P
– ймовірність реалізації цих ДФ, а
∏∏
∀ ∀
−=
$$
j l
ikjlik
PP )1(
,
де j приймає значення номерів ДФ, для протидії яким в системі захисту
передбачені засоби захисту; l – значення н омер ів тих засобів захисту
інформації, які діють на ДФ з н о м ер о м j;
ikjl
P
– й мовірність їх подолання.
