Анищенко В.С. Нелинейные эффекты в хаотических и стохастических системах
Подождите немного. Документ загружается.


x(t) =
Z
t
0
a(t
1
)dt
1
, a(t),
da(t)
dt
, . . . ,
d
n−2
a(t)
dt
n−2
x(t) =
Z
t
0
a(t
1
)dt
1
, a(t), a(t + τ ), . . . , a(t + (n − 2)τ)

0 2 4
−1.5
2.0
t
x
2
−0.5 0.6
−1.5
2.0
x
x
2
1
0 2 4
−1.5
2.0
t
x
2
−0.5 0.6
−1.5
2.0
x
x
2
1
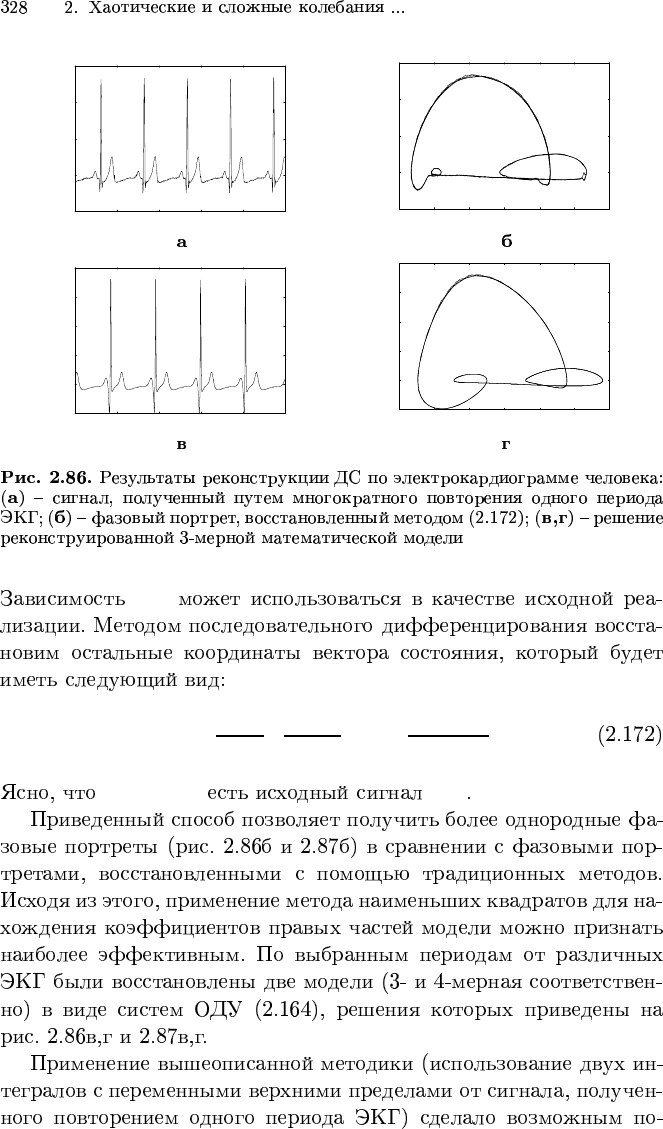
P, Q, R, S, T
QRS P T
R
a(t)
b(t) =
Z
t
0
a(t
1
)dt
1
, c(t) =
Z
t
0
b(t
1
)dt
1
.
0 2 4
−100
300
t
x
3
−4 5
−100
300
x
x
2
3
0 2 4
−100
400
t
x
3
−5 4
−100
400
x
x
2
3
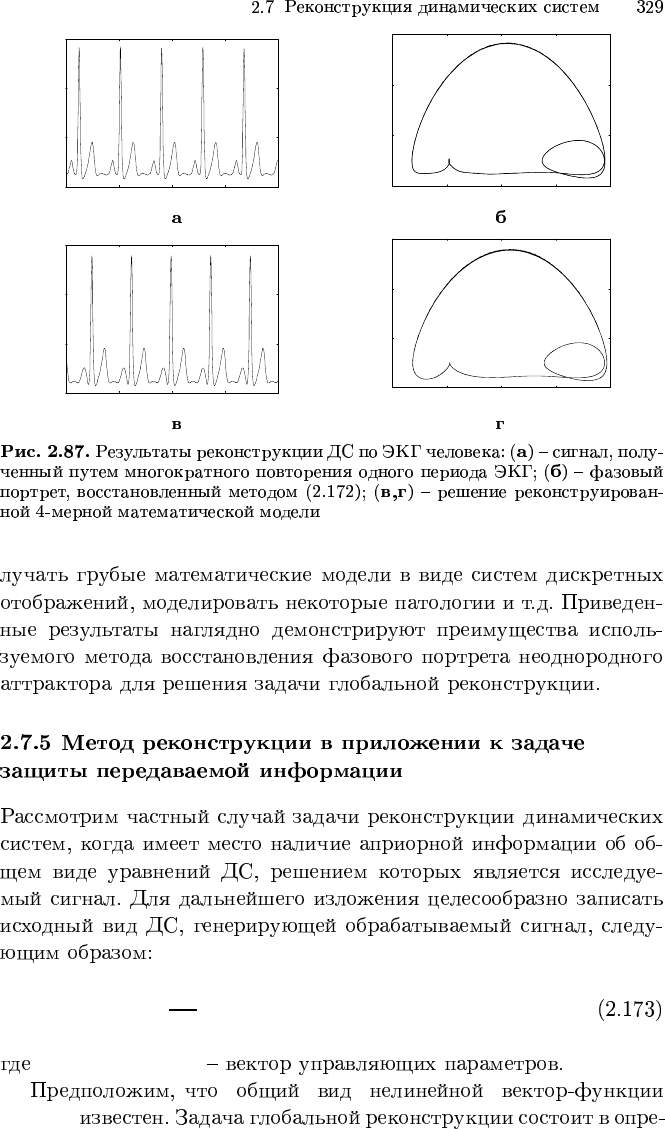
c(t)
x(t) =
c(t) ,
dc(t)
dt
,
d
2
c(t)
dt
2
, . . . ,
d
n−1
c(t)
dt
n−1
.
d
2
c(t)/dt
2
a(t)
0 1 2 3
−50
250
x
3
t
−6 4
−50
250
3
2
x
x
0 1 2 3
−50
250
x
3
t
−6 4
−50
250
x
x
3
2
dx
dt
= F (x, µ), x ∈ R
n
, µ ∈ R
m
,
µ = (µ
1
, . . . , µ
m
)
F (x, µ)

µ
i
2%
G
1
µ
i
m
µ
∗
i
(t) = µ
0
i
+ µ
i
(t), i = 1, . . . , m.

µ
0
i
µ
i
(t)
dµ
i
dt
dx
j
dt
,
i j
dx
dt
= F (x, µ
∗
(t)) .
x
1
(t)
F (x, µ)
t
∗
µ
∗
i
t
∗
x
1
(t)
G
1
µ
i
(t)
µ
i
(t)
x
1
(t)
t
∗
n
x
j
(t), j = 2, . . . , n
x
1,i
= x
1
(i∆t) i = 1, . . . , N
∗
N
∗
=
t
∗
/∆t
i∆t
dx
n,i
dt
= f(x
i
, µ
∗
)
dx
n,i
/dt
n
i = 1, . . . , N
∗
N
∗
m
N
∗
m
µ
∗
i

x
n+1,1
= x
n,2
, x
n+1,2
= x
n,3
, . . . , x
n+1,n
= f(x
n
, µ) .
x
n+1
= 1 − ax
2
n
+ y
n
, y
n+1
= bx
n
.
y
i
, i = 1, . . . , N
∗
y
n+1
= z
n
, z
n+1
= b − az
2
n
/b + by
n
.
a b
y
n
, y
n+1
y
n+2
y
n+3
x(t) y(t)
a b
dx
dt
= m
0
x + y −xz ,
dy
dt
= −x ,
dz
dt
= −g
0
z + 0.5g
0
(x + |x|)x .
y(t)
dY
dt
= Z ,
dZ
dt
= X ,
dX
dt
= f(X, Y, Z, µ) , µ = (m
0
, g
0
) ,

0 9000
1.42
1.38
a
n
0 9000
0.32
0.28
b
n
0 9000
−0.6
0.6
y
n
n
0 9000
1.38
1.42
a
n
0 9000
0.28
0.32
b
n
f(X, Y, Z, µ) =
X(X + Y )
Z
+ (m
0
g
0
− 1)Z − g
0
(X + Y )
+0.5g
0
(|Z| − Z)Z
2
,
Y = y , Z = −x , X = −m
0
x − y + xz .
m
0
g
0
10
−5
1.0
0 1000
1.5
m
t
g
t0 1000
0.14
0.18
0.22
0 1000
-5
5
15
t
y
t
m
0 1000
1.0
1.5
0 1000
0.14
0.18
0.22
g
t
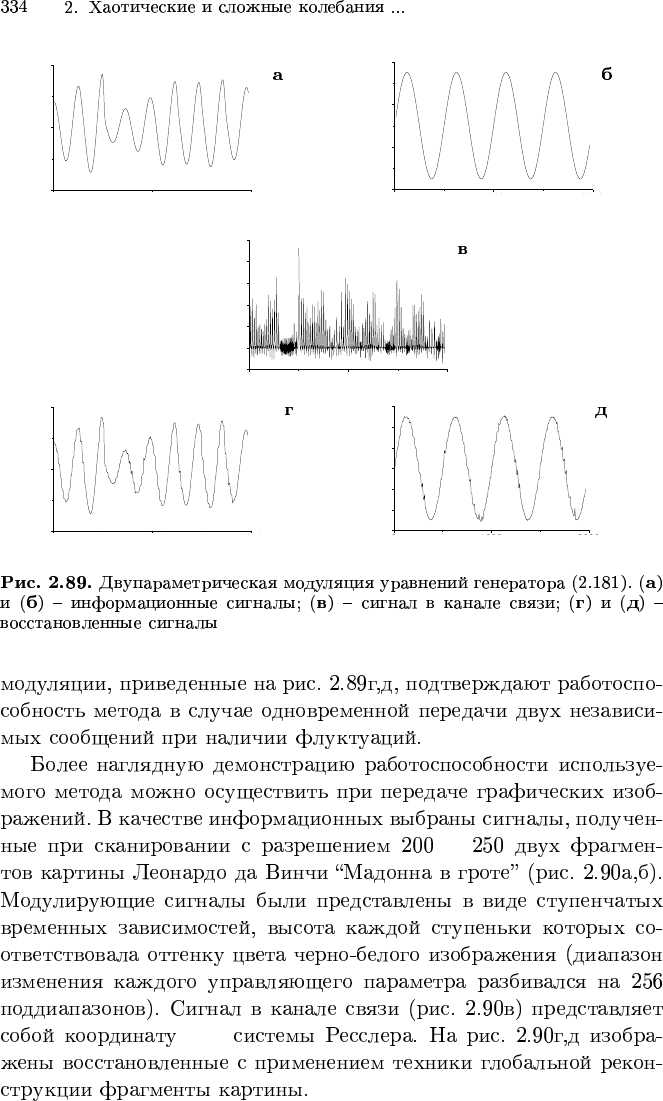
×
y(t)

b c
