Анищенко В.С. Нелинейные эффекты в хаотических и стохастических системах
Подождите немного. Документ загружается.

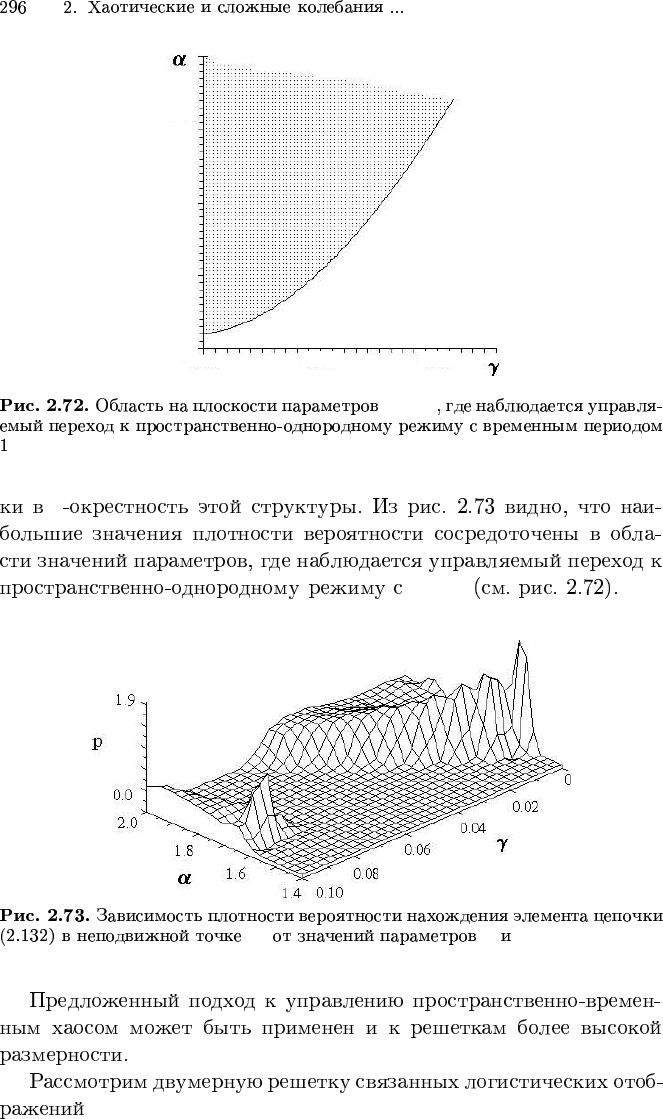
0.00 0.02 0.04
1.6
1.7
1.8
1.5
(α−γ)
ε
T = 1
¯x
1
α γ

x
n+1
(i, j) = α − x
2
n
(i, j) + γ[4x
2
n
(i, j) −x
2
n
(i − 1, j) −
− x
2
n
(i + 1, j) − x
2
n
(i, j − 1) − x
2
n
(i, j + 1)],
x
n
(1, j) = x
n
(N + 1, j)
x
n
(i, 1) = x
n
(i, N + 1) i, j = 1, 2, . . . , N N × N
α γ
T = s
T = 2
λ = 2 T = 2
˜α
n+k−1
(i, j) = 2¯x
k
(1 − 4γ)(x
n+k−1
(i, j) − ¯x
k
) + γ((x
2
n+k−1
(i − 1, j) −
− ¯x
2
k
) + (x
2
n+k−1
(i + 1, j) − ¯x
2
k
) + (x
2
n+k−1
(i, j − 1) − ¯x
2
k
) +
+ (x
2
n+k−1
(i, j + 1) − ¯x
2
k
)),
k = 1, 2, . . . , s, ¯x
k
T = s
T = s

˜α
n
(i, j) = 2p
1
(i, j)(1 − 4γ)[x
n
(i, j) −p
1
(i, j)] + γ[[x
2
n
(i + 1, j) −
− p
2
2
(i, j)] + [x
2
n
(i − 1, j) − p
2
2
(i, j)] + [x
2
n
(i, j − 1) − p
2
2
(i, j)] +
+ [x
2
n
(i, j + 1) − p
2
2
(i, j)]],
˜α
n+1
(i, j) = 2p
11
(i, j)(1 − 4γ)[x
n+1
(i, j) − p
11
(i, j)] +
+ γ[[x
2
n+1
(i + 1, j) − p
2
21
(i, j)] + [x
2
n+1
(i − 1, j) − p
2
21
(i, j)] +
+ [x
2
n+1
(i, j + 1) − p
2
21
(i, j)] + [x
2
n+1
(i, j − 1) − p
2
21
(i, j)] +
+ [x
2
n+1
(i, j + 1) − p
2
21
(i, j)]],
p
1
(i, j) =
¯x
1
,
¯x
2
,
p
2
(i, j) =
¯x
2
, (i + j)
,
¯x
1
, (i + j) ,
p
11
(i, j) =
¯x
11
,
¯x
21
,
p
21
(i, j) =
¯x
21
, (i + j)
,
¯x
11
, (i + j)
¯x
1
, ¯x
2
, ¯x
11
, ¯x
12
20 × 20
α = 1.7 γ = 0.01

T = 1

r > −1
r < −1


a(t)

∆t a(i∆t) = a
i
i = 1, . . . , N
a
i
a
i
a(t)
A

d
a
i
a(t) A
M
n A
R
x(t) R
n
x(t) = Λ
n
[a(t)] =
a(t), a(t+τ), . . . , a(t+(n−1)τ)
= (x
1
, x
2
, . . . , x
n
) ,
n
n > 2M + 1 ,
M
d Λ
n
: A → A
R
A
R
τ
N → ∞ n

n
d
n
d
D
c
= lim
ε→0
lim
N→∞
ln C(ε, N)
ln ε
.
C(ε, N) = N
−2
P
i6=j
v(ε− | x
i
− x
j
|)
ε N
v
x
i
= x(i∆t) x
n n
N
2
ε D
c
ln C(ε, N) ln ε
D
c
n D
c
ε ε
ε
max
ln C(ε, N) ln ε
ε
ε ε = ε
max
C(ε, N) = 1
ln C(ε, N ) = 0 N
ε ε
min
ε < ε
min
ln C(ε, N) ln ε
