Анищенко В.С. Нелинейные эффекты в хаотических и стохастических системах
Подождите немного. Документ загружается.


T
2
N N ≥ 3
˙
x = F(x, α),
F j = 1, 2, . . . , N
C
k
, k ≥ 3 α
α = α
0
T
2
(α
0
)
W
u
C
sd
(α
0
)
C
st
(α
0
) T
2
(α
0
) = W
u
(α
0
)
S
C
st
(α
0
)
α = α
1
α(s) s ∈ [0, 1], α(0) = α
0
, α(1) = α
1
s = s
∗
α(s
∗
)
s
∗
s > s
∗
T
2
0 ≤ s < s
∗
T
2
(α(s))
s > s
∗
W
u
(α(s)) C
st
C
sd

W
u
W
s
C
sd
C
st
A
B
C
C ’
l
l
0
2
l
h
l
1
l
h
l
1
T
2
T
2
A, B, C
T
2
C
st
W
u
W
s
C
sd
C
st
C
sd
s > s
∗∗
T
2
(α(s > s
∗∗
))
α
1
α
2
A, B, C
l
0
l
1
l
2
C
st
l
h
W
u
W
s
C
0
l
1
A l
2
C
st

C
st
T
2
A
l
2
B
W
u
l
h
W
s
s = s
∗
Γ
0
T
2
s > s
∗
C
st
l
h
C
W
u
C
st
l
1
C
st
C
sd
C
sd
C
st
T
2
A, B, C

T
2

L
Q
Q
Q
Q
~
~
~
σ
σ
L
Q
L
L
φ
n+1
= Φ(φ
n
, α), mod 1,
α
Q σ
˜σ
L
φ
n+1
= Φ(φ
n
, Ω, K) = φ
n
+ Ω −
K
2π
sin (2πφ
n
), mod 1,
φ [0; 1] K ≥ 0 Ω ∈ [0; 1]

Φ(φ)
Φ(φ + 1) = 1 + Φ(φ) K < K
cr
Φ(φ)
Φ
−1
(φ)
K = K
cr
Φ
−1
(φ) φ = 0 K > K
cr
K
cr
= 1
θ
θ = lim
n→∞
Φ
n
(φ
0
) − φ
0
n
.
0 ≤ K < 1
φ
0
θ
θ = p/q p q
q
q p
q
θ
Ω
θ
θ K = 0
Ω
0 ≤ K < 1
K
K = 1
K = 1

K > 1
θ(Ω)
T
2
Φ(φ)
θ =
1
m
1
+
1
m
2
+
1
...
= hm
1
, m
2
, . . . , m
k
, . . .i.
k
θ
k
= p
k
/q
k
θ k
θ = lim
k→∞
θ
k
.
θ
g
= 0.5(
√
5 − 1) = h1, 1, 1, . . .i
1
p
k
q
k
p
k
= F
k
, q
k
= F
k+1
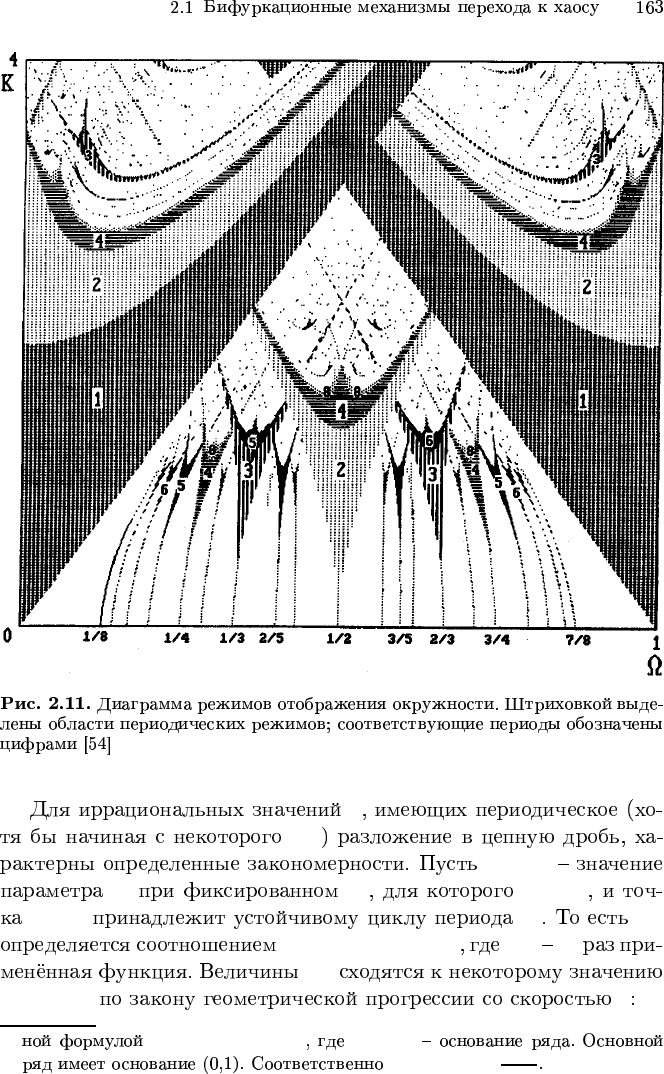
θ
m
k
Ω
k
(K)
Ω K θ = θ
k
φ = 0 q
k
Ω
k
Φ
q
k
(0, Ω
k
, K) = p
k
Φ
q
k
q
k
Ω
k
Ω
∞
(θ, K) δ
F
k+1
= F
k−1
+ F
k
(F
0
, F
1
)
θ
g
= lim
k→∞
F
k
F
k+1

δ = lim
n→∞
Ω
k
− Ω
k−1
Ω
k+1
− Ω
k
.
δ
θ K
δ = −2.6180339 . . . = −θ
−2
g
K < K
cr
δ = −2.83362 . . .
K = K
cr
d
k
= Φ
q
k−1
Ω
k
(0, Ω
k
, K) −
p
k−1
lim
k→∞
d
k
d
k+1
= a,
a θ = θ
g
a = −1.618 . . . = −θ
−1
g
K < K
cr
a = −1.28857 . . . K = K
cr
K = K
cr
θ
θ = θ
g
ν = |F
k+1
θ
g
− F
k
|,
F
k
, F
k+1
j → ∞
S
i
= lim
j→∞
S
j
i
ν
2
(j)
= const.
a
j
i
= S
j
i
/(S
1
1
ν
2
(j))
log a
j
i
− log ν
N ≥ 2

θ = θ
g
Φ
∗
(φ) = a Φ
∗
(aΦ
∗
(φ/a
2
)),
Φ
∗
(φ + 1) = Φ
∗
(φ) + 1 Φ
∗
(φ)
a
Φ
∗
(φ) = φ − 1
a
1,2
= 0.5(±
√
5 − 1)
K < K
cr
a
2
= 0.5(−
√
5 − 1) = −θ
−1
g
≈ −1.618 K = K
cr
Φ(φ)
Φ
∗
(φ)
φ
3
Φ
∗
(φ) = 1 + c
1
φ
3
+ c
2
φ
6
+ . . . .
a
δ
θ = θ
g
Φ
∗
(φ) a δ
θ
N = 3
