Angermann L. (ed.). Numerical Simulations - Applications, Examples and Theory
Подождите немного. Документ загружается.


A General Algorithm for Local Error Control in the RKrGLm Method
481
where the index i refers to the components of the indicated vectors (so
1, ,ri
w is the ith
component of
1,r
w , etc). Call this maximum
1
M
and say it occurs for ik
=
. Hence,
1, , 1, ,
1
1, ,
rk qk
qk
ww
M
w
−
= (3.7)
is the largest relative error in the components of
1,r
w . Note that k may vary from node to
node, but at any particular node we will always intend for
k to denote the maximum value
of (3.6). We now demand that
11,,1,,1,,
RrkqkRqk
Mwww
δδ
≤⇒ − ≤ (3.8)
where
R
δ
is a user-defined relative tolerance. If this inequality is violated we find a new
stepsize
*
0
h such that
()
1
1
1
1, ,
**
01,01,,
1,
0.9
r
r
Rqk
kRqk
k
w
hLhw
L
δ
δ
+
+
⎛⎞
⎛⎞
⎜⎟
=⇒<
⎜⎟
⎜⎟
⎜⎟
⎝⎠
⎝⎠
(3.9)
where
1,k
L is the kth component of
1
L
, and then we find new solutions
1,r
w and
1,q
w
using
*
0
h (
1
L
is determined from (3.5)). The factor 0.9 in (3.9) is a safety factor allowing for
the fact that
1,q
w
is not truly exact. To cater for the possibility that any component of
1,q
w
is close to zero we actually demand
{
}
1, , 1, , 1, ,
max ,
rk qk A R qk
ww w
δδ
−≤ (3.10)
where
A
δ
is a user-defined absolute tolerance. We then set
*
10
hh
=
and proceed to the node
2
x , where the error control process is repeated, and similarly for
3
x up to
m
x . The process
of recalculating a solution using a new stepsize is known as a step rejection.
In the event that the condition in (3.10) is satisfied, we still calculate a new stepsize
*
0
h
(which would now be larger than
0
h ) and set
*
10
hh
=
, on the assumption that if
*
0
h satisfies
(3.10) at
1
x , then it will do so at
2
x as well (however, we also place an upper limit on
*
0
h of
0
2h , although the choice of the factor two here is somewhat arbitrary). In the worst-case
scenario we would find that
1
h is too large and a new, smaller value
*
1
h must be used. The
exception occurs when
1, , 1, ,
0
rk qk
ww
−
= . In this case we simply set
10
2hh
=
and proceed
to
2
x .
The above is nothing more than well-known local relative error control in an explicit RK
method using local extrapolation. It is at the GL node
p
x that the algorithm deviates from
the norm. A step-by-step description of the procedure at
p
x follows:
1.
Once error control at
{
}
12
,,,
m
xx x… has been effected (which necessarily defines the
positions of
{
}
12
,,,
m
xx x… due to stepsize modifications that may have occurred), the
location of
p
x must be determined such that the local relative error at
p
x is less than
{
}
,,
max ,
AR pqk
w
δδ
, in which k has the meaning discussed earlier.

Numerical Simulations - Applications, Examples and Theory
482
2. To this end, we utilize the map (2.8), demanding that
(
)
0
xu
=
corresponds to
1−
on the
interval 1,1
−
⎡⎤
⎣⎦
, and
m
x corresponds to the largest root
m
x
of the mth-degree Legendre
polynomial in 1,1
−
⎡
⎤
⎣
⎦
. This allows
(
)
p
xv
=
to be found, where
p
x corresponds to 1 on
1,1−
⎡⎤
⎣⎦
, and so new nodes
{
}
** *
12 1
,,,
m
xx x
−
… can be determined such that
{
}
** *
12 1
,,, ,
mm
xx x x
−
… are consistent with the GL quadrature nodes on
0
,
p
xx
⎡
⎤
⎣
⎦
.
3.
We wish to perform GL quadrature, using the nodes
{
}
** *
12 1
,,, ,
mm
xx x x
−
… , on
0
,
p
xx
⎡⎤
⎣⎦
,
but we do not have the approximate solutions
{
}
**
1, 1,
,,
qmq
ww
−
… at
{
}
** *
12 1
,,,
m
xx x
−
… .
4.
Hence, we construct the Hermite interpolating polynomial
(
)
P
Hx
on
0
,
m
xx
⎡
⎤
⎣
⎦
using
the original nodes
{
}
12
,,,
m
xx x… and the solutions that have been obtained at these
nodes; of course, the derivative of
(
)
y
x at these nodes is given by
(
)
,fxy. Note that a
Hermite polynomial must be constructed for each of the
s components of the system, so
if 1
d > ,
(
)
P
Hx is actually a 1d
×
vector of Hermite polynomials.
5.
We use the qth-order solutions that are available, so that we expect the approximation
error in each
(
)
P
Hx
to be
(
)
q
Oh , as shown in (2.4) and (2.17).
6.
The solutions
{
}
**
1, 1,
,,
qmq
ww
−
… at
{
}
** *
12 1
,,,
m
xx x
−
… are then obtained from
(
)
(
)
{
}
**
11
,,
PPm
Hx Hx
−
… .
7.
GL quadrature then gives
p
w with local error
(
)
21m
Oh
+
, as per (2.12).
8.
The tandem method RKq is used to find
,
p
q
w , and
,
p
pq
ww− is then used for error
control:
a. we know that the local error in
p
w is
(
)
21m
Oh
+
, where h here is the average node
separation on
0
,
p
xx
⎡
⎤
⎣
⎦
;
b. if the local error is too large then a new average node separation
*
h is determined;
using
*
h , a new position for
p
x , denoted
*
p
x , is found from
**
0p
xx
p
h=+ ;
c. if
*
p
m
xx> , we redefine the nodes
{
}
** *
12 1
,,, ,
mm
xx x x
−
… , find qth-order solutions at
these new nodes using
(
)
P
Hx, and then find solutions at
*
p
x using GL quadrature
and RK
q;
d. if
*
p
m
xx≤ , we reject the GL step since there is now no point in finding a solution at
*
p
x .
9.
After all this, the node
*
p
x or
m
x (if
*
p
m
xx≤ ) defines the endpoint of the subinterval
1
H ; the stepsize h is set equal to the largest separation of the nodes on
1
H , and the
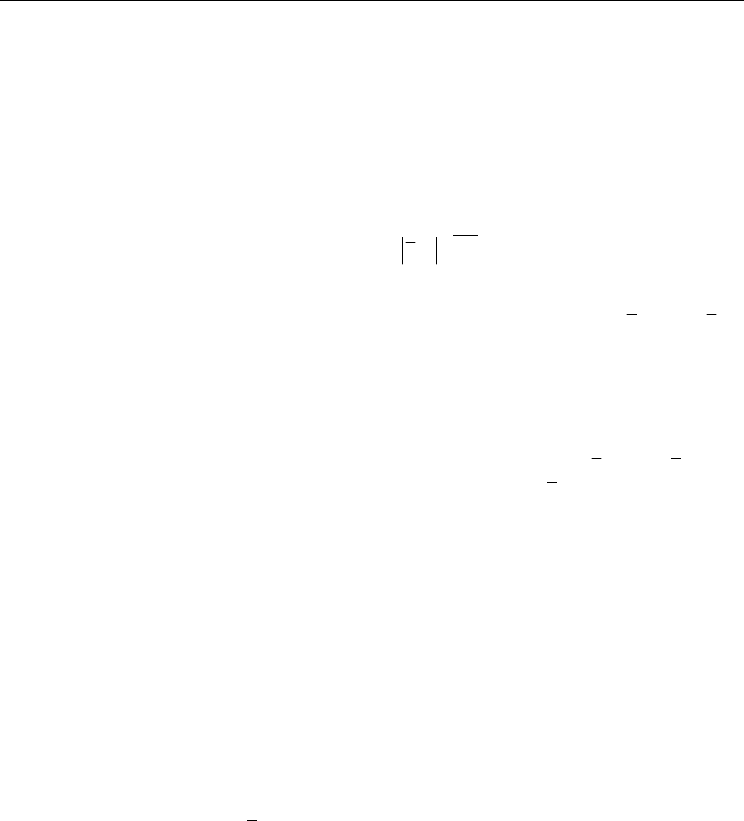
A General Algorithm for Local Error Control in the RKrGLm Method
483
entire error control procedure is implemented on the next subinterval
2
H . Note also
that it is the
qth-order solution at the endpoint of
1
H that is propagated in the RK
solution at the next node.
3.3 Initial stepsize
To find a stepsize
0
h to begin the calculation process, we assume that the local error
coefficient
1,
1
k
L = and then find
0
h from
{}
(
)
1
1
00,
max ,
r
AR k
hy
δδ
+
= (3.11)
Solutions obtained with RK
r and RKq using this stepsize then enable a new, possibly larger,
0
h to be determined, and it is this new
0
h that is used to find the solutions
1,r
w and
1,q
w
at the node
1
x .
3.4 Final node
We keep track of the nodes that evolve from the stepsize adjustments, until the end of the
interval of integration
b has been exceeded. We then backtrack to the node on
,
ab
⎡⎤
⎣⎦
closest
to
b (call it
1
f
x
−
), determine the stepsize
11
f
f
hbx
−
−
≡
− , and then find
,br
w and
,bq
w , the
numerical solutions at
b using RKr and RKq, with
1
f
h
−
,
1
f
x
−
and
1,
f
q
w
−
as input for both
RK
r and RKq. This completes the error control procedure.
4. Comments on embedded RK methods and continuous extensions
Our intention has been to develop an effective local error control algorithm for RKrGLm,
and we believe that the above-mentioned algorithm achieves this objective. Moreover, the
algorithm is general in the choice of RK
r and RKq. These two methods could be entirely
independent of each other, or they could constitute an embedded pair, as in RK(
r,q). This
latter choice would require fewer stage evaluations at each RK node, and so would be more
efficient than if RK
r and RKq were independent. Nevertheless, the use of an embedded pair
is not necessary for the proper functioning of our error control algorithm.
The option of constructing
()
P
Hx using the nodes
121
{,,,}
mp p p
xxx x
−
−
=
… for error control
at
2
p
x (as opposed to using
21
{,, }
pp
xx
−
… ) is worth considering. Such a polynomial,
together with the Hermite polynomial constructed on
01
{,,, }
m
xx x… , forms a piecewise
continuous approximation to
(
)
y
x
on
021
[, ]
p
xx
−
. Of course, this process is repeated at the
nodes
221 31
{, ,, }
pp p
xx x
+−
… , and so on. In this way the Hermite polynomials, which must be
constructed out of necessity for error control purposes, become a piecewise continuous (and
smooth) extension of the approximate discrete solution. Such an extension is not constructed
a posteriori; rather, it is constructed on each subinterval
i
H as the RKrGLm algorithm
proceeds, and so may be used for event trapping.
5. Numerical examples
We will use RK5GL3 to demonstrate the error control algorithm. In RK5GL3 we have
5, 3
rm== so that the tandem method must be an eighth-order RK method, which we

Numerical Simulations - Applications, Examples and Theory
484
denote RK8. The RK5 method in RK5GL3 is due to Fehlberg (Hairer et al., 2000), as is RK8
(Hairer et al., 2000; Butcher, 2003).
By way of example, we solve
2
2
1
'2
1
y
y
x
=−
+
(5.1)
on 0,5
⎡⎤
⎣⎦
with
()
00y
=
, and
'1
420
y
y
y
⎛⎞
=−
⎜⎟
⎝⎠
(5.2)
on 0,30
⎡⎤
⎣⎦
with
(
)
01y
=
. The first of these has a unimodal solution on the indicated interval,
and we will refer to it as IVP1. The second problem is one of the test problems used by Hull
et al (Hull et al., 1972), and we will refer to it as IVP2. These problems have solutions
()
()
2
/4
IVP1:
1
20
IVP2:
119
x
x
yx
x
yx
e
−
=
+
=
+
(5.3)
In Table 1 we show the results of implementing our local error control algorithm in solving
both test problems. The absolute tolerance
A
δ
was always
10
10
−
, except for IVP1 with
10
10
R
δ
−
= , for which
12
10
A
δ
−
= was used.
IVP1
R
δ
4
10
−
6
10
−
8
10
−
10
10
−
RK step rejections 2 2 0 2
GL step rejections 2 5 10 19
nodes 12 20 37 79
RKGL subintervals 4 6 12 25
IVP2
R
δ
4
10
−
6
10
−
8
10
−
10
10
−
RK step rejections 2 2 4 5
GL step rejections 2 3 5 9
nodes 10 19 39 87
RKGL subintervals 3 6 11 24
Table 1. Performance data for error control algorithm applied to IVP1 and IVP2.
In this table, RK step rejections is the number of times a smaller stepsize had to be determined
at the RK nodes; GL step rejections is the number of times that
43
xx
∗
≤
, as described in the
previous section; nodes is the total number of nodes used on the interval of integration,
including the initial node
0
x ; and RKGL subintervals is the total number of subintervals
i
H
used on the interval of integration. It is clear that as
R
δ
is decreased so the number of nodes
and RKGL subintervals increases (consistent with a decreasing stepsize), and so there is
A General Algorithm for Local Error Control in the RKrGLm Method
485
more chance of step rejections. There are not many RK step rejections for either problem.
When
10
10
R
δ
−
= the GL step rejections for IVP1 are 19 out a possible 25 (almost 80%), but
for IVP2 the GL step rejections number only about 38%). In both cases the GL step rejections
arise as a result of relatively large local error coefficients at the GL nodes, which necessarily
lead to relatively small values of h, the average node separation, so that the situation
*
43
xx≤
is quite likely to occur.
Figures 2 and 3 show the RK5GL3 local error for IVP1 and IVP2. The curve labelled tolerance
in each figure is
Ri
y
δ
, which is the upper limit placed on the local error.
x
012345
Error
10
-9
10
-8
10
-7
10
-6
to lera n ce
actual error
IV P 1
Fig. 2. RKGL local error for IVP1, with
6
10
R
δ
−
= .
x
0 5 10 15 20 25 30
Error
10
-9
10
-8
10
-7
actual error
to leran ce
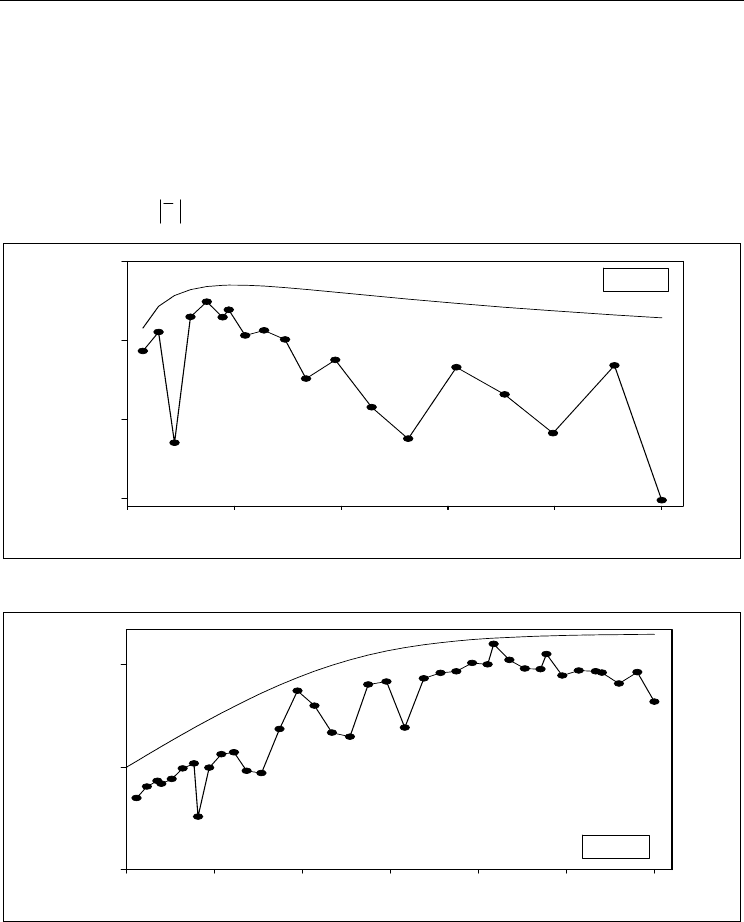
IV P 2
Fig. 3. RKGL local error for IVP2, with
8
10
R
δ
−
=
.
In Figure 2 we have used
6
10
R
δ
−
=
, and in Figure 3 we have used
8
10
R
δ
−
=
. It is clear that
in both cases the tolerance has been satisfied, and the error control algorithm has been
successful. In Figure 4, for interest's sake, we show the stepsize variation as function of node
index (#) for these two problems.

Numerical Simulations - Applications, Examples and Theory
486
#
0 5 10 15 20 25 30 35 40
h
0.0
0.2
0.4
0.6
0.8
1.0
1.2
IV P1
IV P2
Fig. 4. Stepsize h vs node index (#) for IVP1 and IVP2.
To demonstrate error control in a system, we use RK5GL3 to solve
() ()
12
2
212
12
sin 2 2
23
0, 0
55
x
y
y
y
exyy
yy
′
=
′
=−+
=
−=−
(5.4)
on 0,3
⎡⎤
⎣⎦
. The solution to this system, denoted SYS1, is
()
()
2
1
2
2
sin 2 cos
5
4sin 3cos
5
x
x
e
y
xx
e
y
xx
=−
=+
(5.5)
The performance table for RK5GL3 local error control applied to this problem is shown in
Table 2.
SYS1
R
δ
4
10
−
6
10
−
8
10
−
10
10
−
RK step rejections 3 5 6 9
GL step rejections 3 4 8 8
nodes 10 25 52 115
RKGL subintervals 3 7 15 31
Table 2. Performance data for error control algorithm applied to SYS1.
The performance is similar to that shown in Table 1. In all calculations reflected in Table 2,
we have used
12
10
A
δ
−
= . The error in the components y
1
and y
2
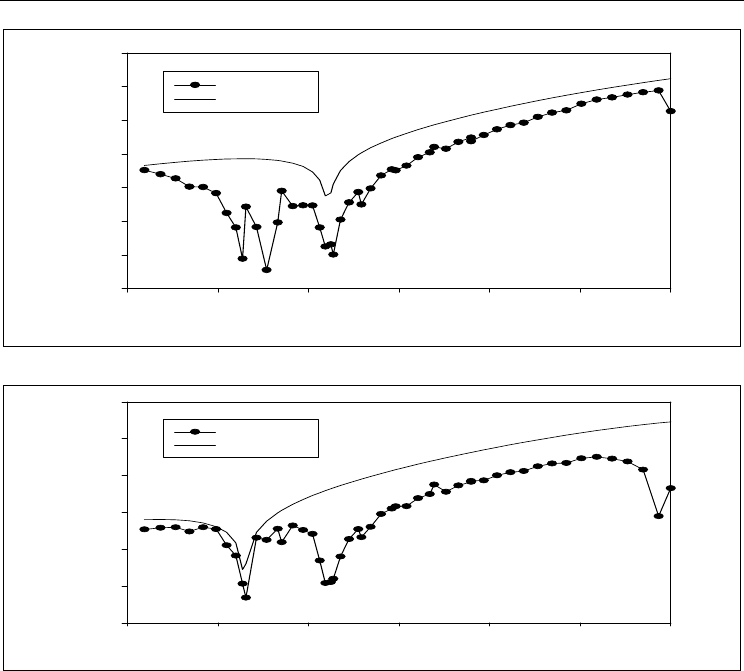
of SYS1 is shown in Figures
5 and 6.
A General Algorithm for Local Error Control in the RKrGLm Method
487
x
0.0 0.5 1.0 1.5 2.0 2.5 3.0
Error
10
-1 2
10
-1 1
10
-1 0
10
-9
10
-8
10
-7
10
-6
10
-5
actual error
to le rance
SYS1
com ponent y
1
Fig. 5. Error in component y
1
of SYS1.
x
0.0 0.5 1.0 1.5 2.0 2.5 3.0
Error
10
-1 1
10
-1 0
10
-9
10
-8
10
-7
10
-6
10
-5
actual error
to leran ce
SY S1
com ponent y
2
Fig. 6. Error in component y
2
of SYS1.
7. Conclusion and scope for further research
We have developed an effective algorithm for controlling the local relative error in RKrGLm,
with 1rm+≤ . The algorithm utilizes a tandem RK method of order 3r
+
, at least. A few
numerical examples have demonstrated the effectiveness of the error control procedure.
7.1 Further research
Although the algorithm is effective, it is somewhat inefficient, as evidenced by the large
number of step rejections shown in the tables. Ways to improve efficiency might include :
a.
The use of an embedded RK pair, such as DOPRI853 (Dormand & Prince, 1980), to
reduce the total number of RK stage evaluations,
b.
Using a high order RKGL method as the tandem method, since the RKGL methods
were originally designed to improve RK efficiency,
c.
Error control per subinterval H
j
, rather than per node, which might require
reintegration on each subinterval,

Numerical Simulations - Applications, Examples and Theory
488
d. Optimal stepsize adjustment, so that stepsizes that are smaller than necessary are not
used. Smaller stepsizes implies more nodes, which implies greater computational effort.
8. References
Burden, R.L. and Faires, J.D., (2001), Numerical analysis, 7th ed., Brooks/Cole, 0-534-38216-9,
Pacific Grove.
Butcher, J.C., (2003), Numerical methods for ordinary differential equations, Wiley, 0-471-96758-
0, Chichester.
Dormand, J.R. and Prince, P.J., A family of embedded Runge-Kutta formulae, Journal of
Computational and Applied Mathematics, 6 (1980) 19-26, 0377-0427.
Hairer, E., Norsett, S.P. and Wanner, G., (2000), Solving ordinary differential equations I:
Nonstiff problems, Springer-Verlag, 3-540-56670-8, Berlin.
Hull, T.E., Enright, W.H., Fellen, B.M. and Sedgwick, A.E., Comparing numerical methods
for ordinary differential equations, SIAM Journal of Numerical Analysis, 9, 4 (1972)
603-637, 0036-1429.
Kincaid, D. and Cheney, W., (2002), Numerical Analysis: Mathematics of Scientific Computing,
3rd ed., Brooks/Cole, 0-534-38905-8, Pacific Grove.
Prentice, J.S.C., The RKGL method for the numerical solution of initial-value problems,
Journal of Computational and Applied Mathematics, 213, 2 (2008) 477-487, 0377-0427.
Prentice, J.S.C.,Improving the efficiency of Runge-Kutta reintegration by means of the RKGL
algorithm, (2009), In: Advanced Technologies, Kankesu Jayanthakumaran, (Ed.), 677-
698, INTECH, 978-953-307-009-4, Vukovar.
22
Hybrid Type Method of Numerical Solution
Integral Equations and its Applications
D.G.Arsenjev
1
, V.M.Ivanov
1
and N.A. Berkovskiy
2
1
Professor, St.Petersburg State Polytechnical University,
2
assoc. prof., St.Petersburg State Polytechnical University,
Russia
1. Introduction
The goal of current research is analysis of the effectiveness of application of semi-statistical
method to the issues, which come up in computational and engineering practice.
The main advantages of this method are the possibility to optimize nodes on the domain of
integration (which makes the work of calculator a lot easier), and also to control the
accuracy of computations with the help of sample variance. Besides this, to improve the
accuracy you can calculate an average solution by statistically independent estimations,
acquired at a small number of integration nodes. A less attractive feature of this method is a
low rate of convergence, which is relevant to all statistic methods.
The reason for this research has become a quite successful application of semi-statistical
method to the test tasks [1, 2, 3]. The problem of plane lattice cascade flow with ideal
incompressible fluid was chosen for simulation. With the help of semi-statistical method
quite precise results have been achieved with the lattices, parameters of which were taken
from engineering practice. These results were compared with the solutions from other
computational methods.
Attempts to accelerate the rate of convergence brought to modernization of the method
(deleting of spikes in average sum). As a result, in all the considered issues solutions with
satisfactory precision were received, adaptive algorithm of lattice optimization was
“putting” the nodes on the domain of integration in accordance with the theoretical
considerations. However, in some cases the solution made by the semi-statistical method
turned out to be longer, than when using deterministic methods, which is caused by
imperfection of software implementation and also with the necessity to look for the new
ways to accelerate rate of convergence for semi-statistical method, in particular,
optimization mechanism.
2. Short scheme of semi-statical method
With semi-statistical method integral equations of the following kind can be solved:
S
xKxyydyfx() (,)() ()
ϕλ ϕ
−=
∫
(1)

Numerical Simulations - Applications, Examples and Theory
490
where S – smooth (m-1)-dimensional surface in R
m
,
xS∈ , yS∈ , R
λ
∈ ,
K - kernel of equation, f - known function, φ- unknown function. This algorithm is described
in detail in [1]. Let us shortly take a look at the scheme of its application in general case.
a. With the help of random number generator on the surface S. N - number of
independent points x
1
, x
2
, …x
N
(vectors) is created with a arbitrary probability density
p(x) (random integration grid).
b. These points are placed one by one in (1), N equations of the kind given below are
received:
ii i
S
xKxyydyfx() (,)() ()
ϕλ ϕ
−=
∫
, (i=1,2,…,N) (2)
c. Integrals in (2) are substituted with the sums by the Monte-Carlo method [1, 2]
and a system of linear algebraic equations appears
N
ij
i
j
i
j
j
ji
Kx x
f
x
Npx
1
(, )
()
1()
λ
ϕϕ
=
≠
−=
−
∑
(3)
Here {φ
i
} (i=1,2,…,N) vector of unknown variables of the system (3). Having solved (3),
φ
i
take for approximated value φ(x
i
) of the solution of integral equation (1)
correspondingly. Approximated value φ(x) xS∀∈ is defined by “retracing” with the
following algorithm:
N
i
i
i
i
Kxx
xfx
Npx
1
(, )
() ()
()
λ
ϕ
ϕ
=
≈+
∑
(4)
The bigger is N the more precisely integrals in (2) are approximated by the finite sum in (3),
which means that we can suppose, that by incrementing value of N is possible to minimize
calculating error of approximation of φ
i
from (3) and φ(x) from (4) in a way that
computation precision requires. As the number of thrown points is sometimes not enough to
reach predefined precision (this number can’t be enlarged infinitively as there is no
possibility to solve to large equation systems), it is recommended to compute m times with
N of thrown points, and then to average the results. This technique gives almost the same
result if we would throw N×m points, because random points in different iterations are
statistically independent.
d.
You can get an estimated value of optimal density of integration nodes by formula [1]
by means of approximated solution φ(x).
()
N
j
j
опт
NN
j
ji j
ji
j
ij
Kx y y
py
pyCN
Kx y y
Kx x x
px
2
1
11
(,)()
()
() ( 1)
(,)()
(,)()
()
ϕ
ϕ
ϕ
=
==
≠
=−
⎧
⎫
⎪
⎪
⎨
⎬
⎪
⎪
⎩⎭
∑
∑∑
(5)
