Анфилатов В.С., Емельянов А.А., Кукушкин А.А. Системный анализ в управлении

Подождите немного. Документ загружается.

Основы системного анализа

Вход системы А

Вход системы В

Л,

Лз

Выход системы А

Выход системы В

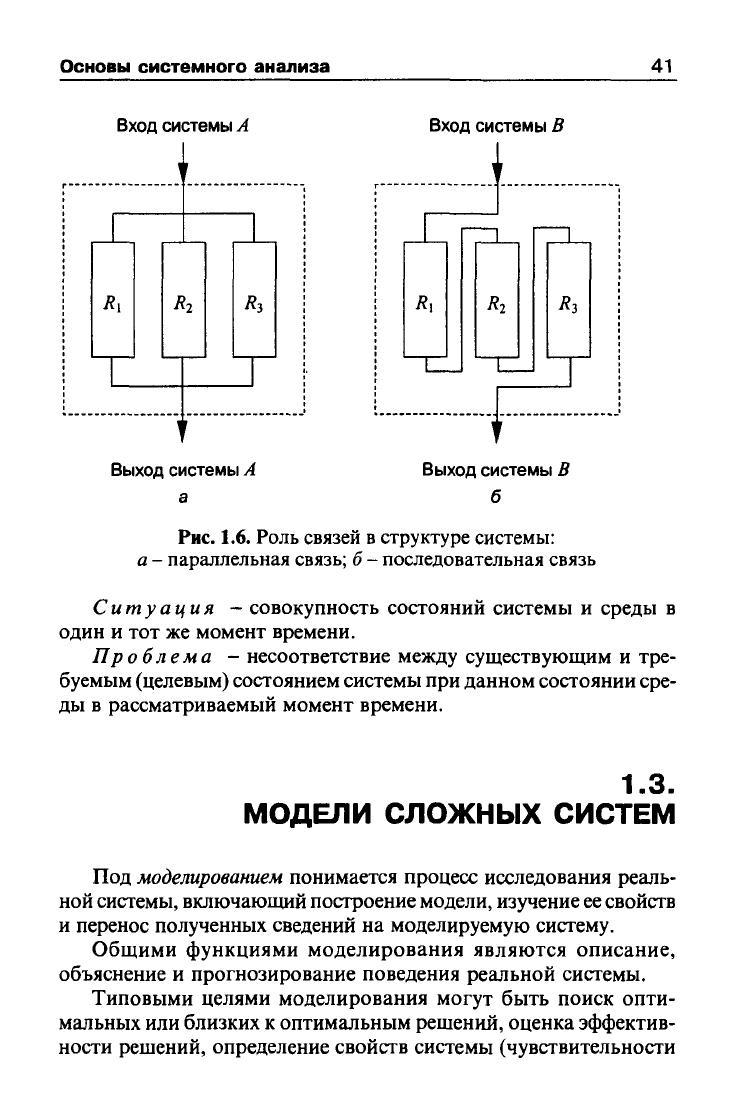
Рис. 1.6. Роль связей в структуре системы:

а - параллельная связь;

- последовательная связь

Ситуация - совокупность состояний системы и среды в

один и тот же момент времени.

Проблема - несоответствие между существующим и тре-

буемым (целевым) состоянием системы при данном состоянии сре-

ды в рассматриваемый момент времени.

1.3.

МОДЕЛИ СЛОЖНЫХ СИСТЕМ

Под

моделированием

понимается процесс исследования реаль-

ной

системы,

включающий построение

модели,

изучение

ее

свойств

и перенос полученных сведений на моделируемую систему.

Общими функциями моделирования являются описание,

объяснение и прогнозирование поведения реальной системы.

Типовыми целями моделирования могут быть поиск опти-

мальных или близких к оптимальным решений, оценка эффектив-

ности решений, определение свойств системы (чувствительности

Глава

к изменению значений характеристик и др.), установление взаи-

мосвязей между характеристиками системы, перенос информа-

ции во времени. Термин «модель» имеет весьма многочисленные

трактовки. В наиболее общей формулировке мы будем придер-

живаться следующего определения модели. Модель - это

объект, который имеет сходство в некоторых отношениях с про-

тотипом и служит средством описания и/или объяснения, и/или

прогнозирования поведения прототипа.

Формальное определение модели (1.1) определяет модель как

изоморфизм А на

*V.

Частные модели могут обозначаться как гомоморфизм:

f: А-^Ч'или

АЛЧ».

Оператор / в этом обозначении указывает на способ, кото-

рый позволяет построить требуемую модель.

Важнейшим качеством модели является то, что она дает уп-

рощенный образ, отражающий не все свойства прототипа, а толь-

ко те, которые существенны для исследования.

Сложные системы характеризуются выполняемыми процес-

сами (функциями), структурой и поведением во времени. Для адек-

ватного моделирования этих аспектов в автоматизированных

информационных системах различают функциональные, инфор-

мационные и поведенческие модели, пересекающиеся друг

с другом.

Функциональная

модель системы описывает совокупность вы-

полняемых системой функций, характеризует морфологию сис-

темы (ее построение) - состав функциональных подсистем, их

взаимосвязи.

Информационная модель отражает отношения между элемен-

тами системы в виде структур данных (состав и взаимосвязи).

Поведенческая (событийная) модель описывает информаци-

онные процессы (динамику функционирования), в ней фигуриру-

ют такие категории, как состояние системы, событие, переход из

одного состояния в другое, условия перехода, последовательность

событий.

Особенно велико значение моделирования в системах, где

натурные эксперименты невозможны по целому ряду причин:

сложность, большие материальные затраты, уникальность, дли-

Основы системного анализа 43

тельность эксперимента. Так, нельзя «провести войну в мирное

время», натурные испытания некоторых типов систем связаны с

их разрушением, для экспериментальной проверки сложных сис-

тем управления требуется длительное время и т.д.

Можно выделить три основные области применения моделей:

обучение, научные исследования, управление. При обучении с

помощью моделей достигается высокая наглядность отображе-

ния различных объектов и облегчается передача знаний о них.

Это в основном модели, позволяющие описать и объяснить сис-

тему. В научных исследованиях модели служат средством полу-

чения, фиксирования и упорядочения новой информации, обес-

печивая развитие теории и практики. В управлении модели ис-

пользуются для обоснования решений. Такие модели должны

обеспечить как описание, так и объяснение и предсказание пове-

дения систем.

1.3.1.

КЛАССИФИКАЦИЯ ВИДОВ

МОДЕЛИРОВАНИЯ СИСТЕМ

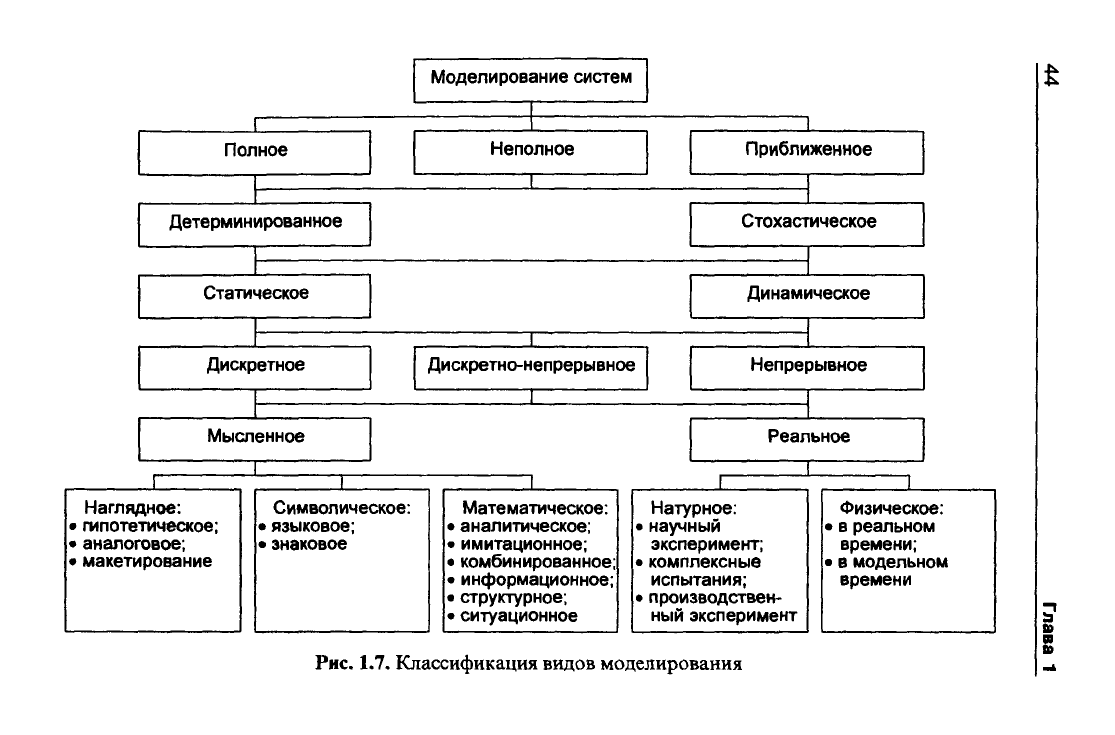
Классификация видов моделирования может быть проведена

по разным основаниям. Один из вариантов классификации при-

веден на рис. 1.7.

В соответствии с классификационным признаком полноты

моделирование делится на полное, неполное и приближенное.

При полном моделировании модели идентичны объекту во вре-

мени и пространстве. Для

неполного

моделирования эта идентич-

ность не сохраняется. В основе приближенного моделирования

лежит подобие, при котором некоторые стороны реального

объекта не моделируются совсем. Теория подобия утверждает,

что абсолютное подобие возможно лишь при замене одного

объекта другим точно таким же. Поэтому при моделировании

абсолютное подобие не имеет места. Исследователи стремятся к

тому, чтобы модель хорошо отображала только исследуемый ас-

пект системы. Например, для оценки помехоустойчивости диск-

ретных каналов передачи информации функциональная и инфор-

мационная модели системы могут не разрабатываться. Для дос-

тижения цели моделирования вполне достаточна событийная

Моделирование систем

Полное

Неполное

Приближенное

Детерминированное

Стохастическое

Статическое

Динамическое

Дискретное

Дискретно-непрерывное Непрерывное

Мысленное Реальное

Наглядное:

' гипотетическое;

' аналоговое;

' макетирование

Символическое:

• языковое;

• знаковое

Математическое:

• аналитическое;

• имитационное;

• комбинированное;

• информационное

• структурное;

• ситуационное

Натурное:

• научный

эксперимент;

• комплексные

испытания;

• производствен-

ный эксперимент

Физическое:

в реальном

времени;

в модельном

времени

Рис.

1.7. Классификация видов моделирования

Основы системного анализа 45

модель, описываемая матрицей условных вероятностей ||pj| пе-

реходов г-го символа алфавита

j-й.

В зависимости от типа носителя и сигнатуры модели разли-

чаются следующие виды моделирования: детерминированное и

стохастическое, статическое и динамическое, дискретное, непре-

рывное и дискретно-непрерывное.

Детерминированное моделирование отображает процессы, в

которых предполагается отсутствие случайных воздействий.

Стохастическое моделирование учитывает вероятностные про-

цессы и события. Статическое моделирование служит для опи-

сания состояния объекта в фиксированный момент времени, а

динамическое

- для исследования объекта во времени. При этом

оперируют аналоговыми (непрерывными), дискретными и сме-

шанными моделями.

В зависимости от формы реализации носителя и сигнатуры

моделирование классифицируется на мысленное и реальное.

Мысленное моделирование применяется тогда, когда модели не

реализуемы в заданном интервале времени либо отсутствуют ус-

ловия для их физического создания (например, ситуация микро-

мира).

Мысленное моделирование реальных систем реализуется

в виде наглядного, символического и математического. Для пред-

ставления функциональных, информационных и событийных

моделей этого вида моделирования разработано значительное

количество средств и методов.

При наглядном моделировании на базе представлений чело-

века о реальных объектах создаются наглядные модели, отобра-

жающие явления и процессы, протекающие в объекте. Примером

таких моделей являются учебные плакаты, рисунки, схемы, диаг-

раммы.

В основу

гипотетического

моделирования закладывается ги-

потеза о закономерностях протекания процесса в реальном объек-

те,

которая отражает уровень знаний исследователя об объекте и

базируется на причинно-следственных связях между входом и

выходом изучаемого объекта. Этот вид моделирования исполь-

зуется, когда знаний об объекте недостаточно для построения

формальных моделей. Аналоговое моделирование основывается

на применении аналогий различных уровней. Для достаточно

простых объектов наивысшим уровнем является полная анало-

гия.

С усложнением системы используются аналогии последую-

46 Глава 1

щих уровней, когда аналоговая модель отображает несколько

(или только одну) сторон функционирования объекта. Макети-

рование применяется, когда протекающие в реальном объекте

процессы не поддаются физическому моделированию или могут

предшествовать проведению других видов моделирования. В ос-

нове построения мысленных макетов также лежат аналогии, обыч-

но базирующиеся на причинно-следственных связях между явле-

ниями и процессами в объекте.

Символическое

моделирование представляет собой искусствен-

ный процесс создания логического объекта, который замещает

реальный и выражает его основные свойства с помощью опреде-

ленной системы знаков и символов. В основе языкового модели-

рования лежит некоторый тезаурус, который образуется из на-

бора понятий исследуемой предметной области, причем этот на-

бор должен быть фиксированным. Под тезаурусом понимается

словарь, отражающий связи между словами или иными элемен-

тами данного языка, предназначенный для поиска слов по их

смыслу.

Традиционный тезаурус состоит из двух частей: списка слов и

устойчивых словосочетаний, сгруппированных по смысловым (те-

матическим) рубрикам; алфавитного словаря ключевых слов, за-

дающих классы условной эквивалентности, указателя отношений

между ключевыми словами, где для каждого слова указаны соот-

ветствующие рубрики. Такое построение позволяет определить

семантические (смысловые) отношения иерархического (род/вид)

и неиерархического (синонимия, антонимия, ассоциации) типа.

Формально тезаурусом называют конечное непустое множе-

ство V слов

отвечающее следующим условиям:

1) имеется непустое подмножество

С V, называемое мно-

жеством дескрипторов;

2) имеется симметричное, транзитивное, рефлексивное отно-

шение Ra Vx V, такое, что:

a)vi^V2nvi^v2=>(vier\Fo)U(v2e^\Fo);

б)

€ F \ Ко

(3v € Vo)(yR

vi)'

при этом отношение R называется синонимическим, а слова Vj,

Vj,

отвечающие этому отношению, называются синонимическими

дескрипторами;

Основы системного анализа 47

3) имеется транзитивное и несимметричное отношение

К а FQXFQ, называемое обобшающим отношением.

В случае если два дескриптора v, и

удовлетворяют отноше-

нию Vj К Vj, то полагают, что дескриптор v, более общий, чем

дескриптор Vj.

Элементы множества VWQ называются множеством аскрип-

торов.

Между тезаурусом и обычным словарем имеются принципи-

альные различия. Тезаурус - словарь, который очищен от нео-

днозначности, т.е. в нем каждому слову может соответствовать

лишь единственное понятие, хотя в обычном словаре одному сло-

ву может соответствовать несколько понятий.

Если ввести условное обозначение отдельных понятий, т.е.

знаки, а также определенные операции между этими знаками, то

можно реализовать знаковое моделирование и с помощью зна-

ков отображать набор понятий - составлять отдельные цепочки

из слов и предложений. Используя операции объединения, пере-

сечения и дополнения теории множеств, можно в отдельных сим-

волах дать описание какого-то реального объекта.

Математическое моделирование - это процесс установления

соответствия данному реальному объекту некоторого математи-

ческого объекта, называемого математической моделью. В прин-

ципе, для исследования характеристик любой системы матема-

тическими методами, включая и машинные, должна быть обяза-

тельно проведена формализация этого процесса, т.е. построена

математическая модель. Вид математической модели зависит как

от природы реального объекта, так и от задач исследования

объекта, от требуемой достоверности и точности решения зада-

чи.

Любая математическая модель, как и всякая другая, описыва-

ет реальный объект с некоторой степенью приближения.

Для представления математических моделей могут исполь-

зоваться различные формы записи. Основными являются инва-

риантная", аналитическая, алгоритмическая и схемная (графи-

ческая).

Инвариантная форма - запись соотношений модели с помо-

щью традиционного математического языка безотносительно к

методу решения уравнений модели. В этом случае модель может

быть представлена как совокупность входов, выходов, перемен-

ных состояния и глобальных уравнений системы в виде (1.3).

48 Глава 1

Аналитическая форма - запись модели в виде результата ре-

шения исходных уравнений модели. Обычно модели в аналити-

ческой форме представляют собой явные выражения выходных

параметров как функций входов и переменных состояния.

Для

аналитического

моделирования характерно то, что в ос-

новном моделируется только функциональный аспект системы.

При этом глобальные уравнения системы, описывающие закон

(алгоритм) ее функционирования, записываются в виде некото-

рых аналитических соотношений (алгебраических, интегродиф-

ференциальных, конечноразностных и т.д.) или логических усло-

вий. Аналитическая модель исследуется несколькими методами:

• аналитическим, когда стремятся получить в общем виде

явные зависимости, связывающие искомые характеристики с на-

чальными условиями, параметрами и переменными состояния

системы;

• численным, когда, не умея решать уравнения

общем виде,

стремятся получить числовые результаты

при

конкретных началь-

ных данных (напомним, что такие модели называются цифро-

выми);

• качественным, когда, не имея решения в явном виде, мож-

но найти некоторые свойства решения (например, оценить устой-

чивость решения).

В настоящее время распространены компьютерные методы

исследования характеристик процесса функционирования слож-

ных систем. Для реализации математической модели на

ЭВМ

не-

обходимо построить соответствующий моделирующий алгоритм.

Алгоритмическая форма -

запись

соотношений модели

выб-

ранного численного метода решения в форме алгоритма. Среди

алгоритмических моделей важный класс составляют имитацион-

ные модели, предназначенные для имитации физических или ин-

формационных процессов при различных внешних воздействи-

ях. Собственно имитацию названных процессов называют ими-

тационным моделированием.

При

имитационном

моделировании воспроизводится алго-

ритм функционирования системы во времени - поведение систе-

мы,

причем имитируются элементарные явления, составляющие

процесс, с сохранением их логической структуры и последова-

тельности протекания, что позволяет по исходным данным полу-

чить сведения о состояниях процесса в определенные моменты

Основы системного анализа 49

времени, дающие возможность оценить характеристики системы.

Основным преимуществом имитационного моделирования по

сравнению с аналитическим является возможность решения бо-

лее сложных задач. Имитационные модели позволяют достаточ-

но просто учитывать такие факторы, как наличие дискретных и

непрерывных элементов, нелинейные характеристики элементов

системы, многочисленные случайные воздействия и другие, ко-

торые часто создают трудности при аналитических исследовани-

ях. В настоящее время имитационное моделирование - наиболее

эффективный метод исследования систем, а часто и единствен-

ный практически доступный метод получения информации о по-

ведении системы, особенно на этапе ее проектирования.

В имитационном моделировании различают метод статисти-

ческих испытаний (Монте-Карло) и метод статистического мо-

делирования.

Метод Монте-Карло - численный метод, который применя-

ется для моделирования случайных величин и функций, вероят-

ностные характеристики которых совпадают с решениями ана-

литических задач. Состоит в многократном воспроизведении

процессов, являющихся реализациями случайных величин и фун-

кций, с последующей обработкой информации методами мате-

матической статистики.

Если этот прием применяется для машинной имитации в це-

лях исследования характеристик процессов функционирования

систем, подверженных случайным воздействиям, то такой метод

называется методом статистического моделирования.

Метод имитационного моделирования применяется для оцен-

ки вариантов структуры системы, эффективности различных ал-

горитмов управления системой, влияния изменения различных

параметров системы. Имитационное моделирование может быть

положено в основу структурного, алгоритмического и парамет-

рического синтеза систем, когда требуется создать систему с за-

данными характеристиками при определенных ограничениях.

Комбинированное (аналитико-имитационное) моделирование

позволяет объединить достоинства аналитического и имитаци-

онного моделирования. При построении комбинированных мо-

делей производится предварительная декомпозиция процесса

функционирования объекта на составляющие подпроцессы, и для

тех из них, где это возможно, используются аналитические моде-

50 Глава 1

ли,

а для остальных подпроцессов строятся имитационные моде-

ли.

Такой подход дает возможность охватить качественно новые

классы систем, которые не могут быть исследованы с использо-

ванием аналитического или имитационного моделирования в

отдельности.

Информационное

{кибернетическое)

моделирование связано с

исследованием моделей, в которых отсутствует непосредствен-

ное подобие физических процессов, происходящих в моделях,

реальным процессам. В этом случае стремятся отобразить лишь

некоторую функцию, рассматривают реальный объект как «чер-

ный ящик», имеющий ряд входов и выходов, и моделируют неко-

торые связи между выходами и входами. Таким образом, в осно-

ве информационных (кибернетических) моделей лежит отраже-

ние некоторых информационных процессов управления, что

позволяет оценить поведение реального объекта. Для построе-

ния модели в этом случае необходимо выделить исследуемую

функцию реального объекта, попытаться формализовать эту фун-

кцию в виде некоторых операторов связи между входом и выхо-

дом и воспроизвести данную функцию на имитационной моде-

ли,

причем на совершенно другом математическом языке и, есте-

ственно, иной физической реализации процесса. Так, например,

экспертные системы являются моделями ЛПР.

Структурное моделирование системного анализа базирует-

ся на некоторых специфических особенностях структур опреде-

ленного вида, которые используются как средство исследования

систем или служат для разработки на их основе специфических

подходов к моделированию с применением других методов фор-

мализованного представления систем (теоретико-множественных,

лингвистических, кибернетических и т.п.). Развитием структур-

ного моделирования является объектно-ориентированное моде-

лирование.

Структурное моделирование системного анализа включает:

• методы сетевого моделирования;

• сочетание методов структуризации с лингвистическими;

• структурный подход в направлении формализации постро-

ения и исследования структур разного типа (иерархических, мат-

ричных, произвольных графов) на основе теоретико-множествен-

ных представлений и понятия номинальной шкалы теории изме-

рений.