Ammari H., Benkirane A., Touzani A. (editors) Recent Developments in Nonlinear Analysis

Подождите немного. Документ загружается.

December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent

110

3.2. The discrete problem

Let us consider that a triangulation T

is deﬁned over Ω, regular in the

sense that each simplex T ∈ T

contains a ball with radius γ

h and is

contained in a ball with radius γ

h where the positive constants γ

and γ

are independent of h.

A piecewise linear subspace V

of V can be deﬁned as:



∈ C



Ω



∩ H

(Ω) such that for all T ∈ T

: v

h|T

∈ P

(T )



Let N = N (h), number of nodes A

of the triangulation, to simplify

the notations, we assume that the numbering is such that A

, A

, . . . , A

are the internal nodes while A

, . . . , A

lie on the boundary Γ. N

then the dimension of V

. We introduce the canonical basis (ϕ

, ϕ

, . . . , ϕ

)

associated to the triangulation T

We assume in addition that the inverse assumption (see

) holds, what

permits to have the following inverse inequality:

(Ω)

≤ ch

−1

(Ω)

, ∀w

∈ V

. (27)

To approximate µ ∈ L

(Ω), we need a discrete space with the same

dimension as V

, so we can use V

or we associate to the triangulation T

the set K

of the N volumes D

(i = 1...N) that constitute the dual of

the triangulation T

known as the Voronoi mesh. This mesh is constructed

by connecting with a straight line segment the mid-points of edges and

centroids of each neighboring pair of triangles having a common edge. And

we introduce the space W

(approximation of L

(Ω) and H

−1

(Ω)), deﬁned

by:



∈ L

(Ω) such that for all D ∈ K

: w

h|D

∈ P

(D)



equipped with its canonical basis (χ

, χ

, ..., χ

), where χ

is the charac-

teristic function of the control volume D

The discrete problem associated to (21) reads:







Find (u

, µ

) ∈ V

× C

such that

a(u

, v

) + hµ

, v

i + (f

−

, v

) = 0, for all v

∈ V

hζ

− µ

, u

i ≤ 0, for all ζ

∈ C

(28)

where we set

(

i=1

∈ W

such that 0 ≤ hζ

, ϕ

i ≤ T

: i = 1 . . . N

)

and T

Ω

dx.

December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent

111

With the notations above it is easy to see that problem (28 ) can be

written as:

(

Find (U, Y ) ∈ R

i=1



0, T



such that

J(U, z) ≤ J (U, Y ) ≤ J(w, Y ), for all (w, z) ∈ R

i=1



0, T



(29)

where we set J(w, z) =

(Mw, w) + (T

−

, w) + (z, w) with T

−

Ω

−

dx and Y = P µ

. M is the stiﬀness matrix of the problem i.e.

M = (m

= a(ϕ

, ϕ

)), P = (p

), is the N

× N

-matrix such that

Ω

dx =

dx. In the one dimensional case and with regu-

lar triangulation, the matrix P is easily calculable and one has:

P =







6 1 0 ··· 0

0 ··· 0 1 6







In the two dimensional case the matrix P is also calculable for a tri-

angulation with simple geometries and it is symmetric. More precisely one

can show, in an elementary manner, the following properties: p

and

j6=i

| for i = 1...N

. To compute p

dx for i = j

or for internal neighboring nodes A

and A

, one can use trapezoid formula

by splitting D

into small triangles and using the fact that the dual mesh

splits any triangle of the primal triangulation into six small triangles having

common measure.

If one uses V

instead of W

to approach µ, the matrix P will be re-

placed by B = (b

), where b

Ω

dx. Using Simpson’s formula, one

can show the following properties: b

| and

j6=i

|, where

[

∈T

T , for all internal node A

, i = 1...N

To use the results of the section (2) we must establish a discrete inf-sup

condition and show that C

approximates C in the sense of.

To this end,

we establish the following technical lemmas.

December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent

112

Lemma 3.1. There exists two positive constants c

, c

independent of h

such that

(Ω)

≤ kα

(Ω)

≤ c

hα

, w

i, (30)

for all α

∈ W

, where w

∈ V

Proof. In 2-D case.

For α =

(α

, ..., α

), α

∈ W

and w

∈ V

, one

has

kα

(Ω)

αDα, kw

(Ω)

αBα, and hα

, w

i =

αP α,

where D is the diagonal matrix D = diag(|D

|, ..., |D

|). So

(Ω)

kα

(Ω)

αBα

αDα

αBα

αα

αDα

≤

, (31)

where t is the largest eigenvalue of B, and s the smallest one of D. By the

regularity assumptions on the triangulation and the properties of B and D,

and thanks to Gershgorin’s theorem, one has

t ≤

max

| ≤ ch

and s ≥ min

| ≥ ch

the ﬁrst inequality of (30) follows.

On the other hand

kα

(Ω)

hα

, w

αDα

αP α

αDα

αα

αP α

≤

, (32)

where t

is the largest eigenvalue of D, and s

the smallest one of P. While

reasoning like previously, the second inequality of (30) follows.

Lemma 3.2. For λ ∈ L

(Ω), if λ

is the projection of λ on W

in the

following sense

Ω

λv

dx =

Ω

dx, ∀v

∈ V

then there exists a positive constant c independent of h and λ such that



λ − λ



−1

(Ω)

≤ ch kλk

(Ω)

. (33)

December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent

113

Proof. For all v ∈ H

(Ω), if v

∈ V

denotes the Lagrange interpolant of

v, one has

Ω

(λ − λ

)vdx =

Ω

(λ − λ

)(v − v

)dx

≤



λ − λ



(Ω)



v − v



(Ω)

≤ ch



λ − λ



(Ω)

kvk

(Ω)

therefore



λ − λ



−1

(Ω)

≤ ch



λ − λ



(Ω)

. (34)

On the other hand, let λ

, and w

, using (30 ), one

has



(Ω)

≤ c

Ω

dx = c

Ω

λw

dx ≤ c kλk

(Ω)



(Ω)

what implies, with the help of (34), the estimate (33).

Lemma 3.3. There exists a constant β independent of h, such that

∀α

∈ W

: sup

∈V

6=0

hα

, v

(Ω)

≥ β kα

−1

(Ω)

. (35)

Proof. For α

i=1

∈ W

, let w ∈ H

(Ω) ∩ H

(Ω) and w

∈ V

such that

−∆w = α

and a(w

, v

) = a(w, v

) = hα

, v

i, ∀v

∈ V

it is known (see

), that kw − w

(Ω)

≤ ch kα

(Ω)

, therefore

kwk

(Ω)

− kw

(Ω)

= kw − w

(Ω)

≤ ch

kα

(Ω)

hence

kα

−1

(Ω)

= kwk

(Ω)

≤ kw

(Ω)

+ ch

kα

(Ω)

. (36)

On the other hand, for v

i=1

∈ V

, using (30) and the inverse

inequality (27), one has

hα

, v

(Ω)

≥ ch kα

(Ω)

, (37)

December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent

114

what permits to conclude, with the help of (36) that

kα

−1

(Ω)

≤ c kw

(Ω)

= c sup

∈V

6=0

hα

, v

(Ω)

If one uses V

instead of W

to approximate µ, the discrete inf-sup condition

would be an immediate consequence of (36) and (27).

Lemma 3.4. The sequence (C

) approximates C in the following sense:

(i) ∀λ ∈ C, ∃λ

∈ C

,such that: λ

→ λ in H

−1

(Ω).

(ii) If λ

∈ C

such that λ

* λ in H

−1

(Ω), for some λ in L

(Ω), then

λ ∈ C.

Proof. Item (i) follows from the estimate (33) and the fact that λ

∈ C

if λ ∈ C.

On the other hand let λ

and λ as in (ii), so for all v ∈ H

(Ω), v ≥ 0

and v

∈ V

, v

≥ 0 such that v

→ v in H

(Ω), one has

0 ≤

Ω

dx ≤

Ω

dx,

however

Ω

dx →

Ω

λvdx, therefore

0 ≤

Ω

λvdx ≤

Ω

vdx,

what permits to conclude that λ ∈ C.

In addition to the results of Section 2, one has the following error esti-

mate.

Theorem 3.1. If (u, µ) and (u

, µ

) designate the respective solutions to

problems (21) and (28), and if u ∈ H

(Ω) then there exists a positive

constant c independent of h such that:

ku −u

(Ω)

+ kµ − µ

−1

(Ω)

≤ ch. (38)

Proof. Using theorem 2.1, and thanks to the interpolation error (see



u −u



(Ω)

≤ ch

kuk

(Ω)

and



u −u



(Ω)

≤ ch kuk

(Ω)

where u

∈ V

denotes the interpolant of u ∈ H

(Ω), and the interpolation

(33):



µ −µ



−1

(Ω)

≤ ch kµk

(Ω)

December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent

115

we had proved, it rests to examine the quantities B

(ζ

) and B

(ζ) that

appear in the inequalities (18) and (19). To this end, let us take ζ

= µ

∈

in B

, we have:

(µ

) =



µ − µ

, u





µ − µ

, u −u



≤



µ − µ



−1

(Ω)



u −u



(Ω)

≤ ch

kµk

(Ω)

kuk

(Ω)

On the other hand, with ζ = µ ∈ C in B

, and while taking into account

the fact that u ≥ 0 a.e. in Ω and

hµ, ui =



, u



we obtain:

(µ) = hµ

− µ, ui = hµ

− f

, u −u

i + hµ

− f

, u

≤ hµ

− f

, u −u

i ( because µ

∈ C

and u

≥ 0)

≤



− f



(Ω)



u −u



(Ω)

≤



− f



(Ω)

kuk

(Ω)

to conclude, we must show that kµ

(Ω)

is bounded independently of h,

more precisely we show that

kµ

(Ω)

≤ c



(Ω)

, (39)

indeed, let µ

i=1

and v

i=1

, one has (lemma 3.1):

kµ

(Ω)

≤ c

hµ

, v

i = c

i=1

Ω

≤ c

i=1

|µ

Ω

dx ≤ c

i=1

|µ

Ω

≤ c

Ω

i=1

|µ

|ϕ

dx ≤ c



(Ω)



i=1

|µ

|ϕ



(Ω)

≤ c



(Ω)



i=1

|µ

|χ



(Ω)

≤ c



(Ω)

kµ

(Ω)

That ﬁnishes the proof.

In the case where one chooses V

instead of W

to approximate µ ,

the inequality (39) can be proved in the same manner by putting µ

i=1

, and using two times the lemma 3.1.

December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent

116

3.3. Some numerical results

In this section, we present two numerical tests in order to conﬁrm the

theoretical results.

Example 1.

We consider the following one-dimensional obstacle problem, with Ω =

]0, 2[, ψ = 0 and f deﬁned by:



f(x) = −1 if x ∈ [0, 1] ,

f(x) = 1 if x ∈ ]1, 2] .

The solution to the continuous problem is calculable. And one has:











u(x) = −

+ (2 −

√

2)x if x ∈ [0, 1] ,

u(x) =

−

√

2x + 1 if x ∈



√



u(x) = 0 if x ∈



√

2, 2



and the measure µ = χ

[

√

]

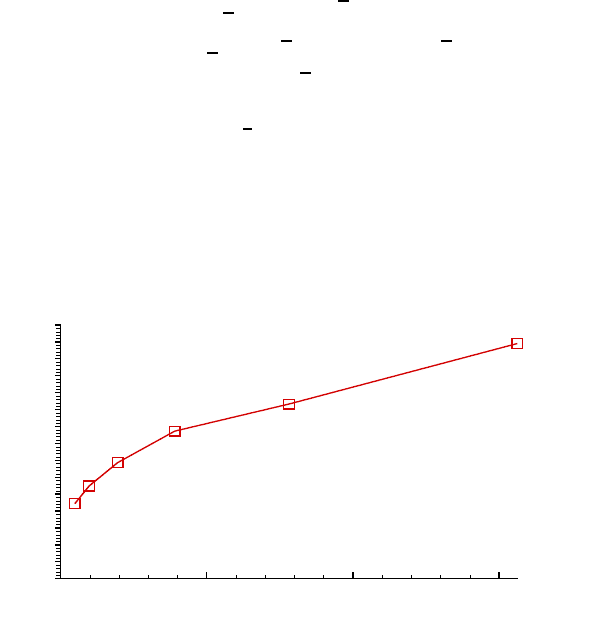
We solve the mixed problem (29) using Uzawa’s algorithm, and for dif-

ferent values of h. Figure 1 bellow represents the L

-error on µ for diﬀerent

values of h.

L2-error on mu

0 0.01 0.02 0.03

0.01

0.02

0.03

0.04

0.05

0.06

0.07

0.08

0.09

0.1

0.11

0.12

0.13

0.14

0.15

Fig. 1. L

-error on µ for diﬀerent values of h.

December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent

117

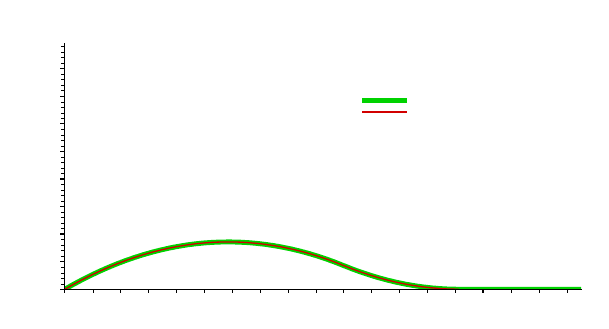
Figure 2 gives a comparison between the curve of u and the one of u

for h = 1/32. One remarks that the two curves are nearly confounded, and

this even though h is not small enough.

u(x)

0 0.5 1 1.5

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

Exact u.

Approched u. h = 1 / 32.

Fig. 2. Comparison between u and u

for h = 1/32.

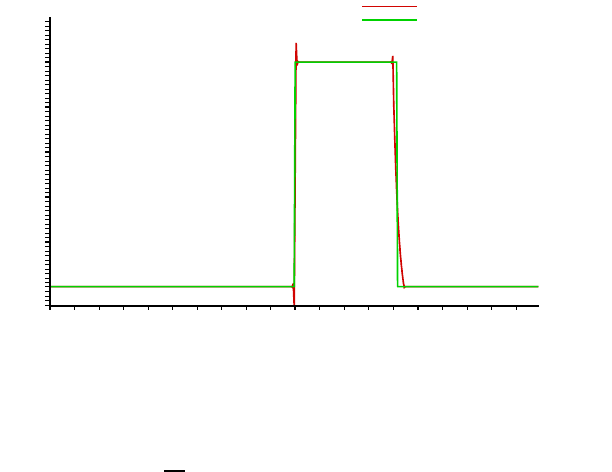
Figure 3 gives a comparison between the curve of µ and the one of µ

for h = 1/256. The oscillations near the value 1 are due to the discontinuity

of f at this point.

The advantage to use µ to characterize the free boundary and not u, is

due to the fact that with µ = F

[u>ψ]

the jump is pronounced (because

under some regularity hypotheses on the obstacle ψ (see

) one has F ≥

c > 0 near the free boundary), what is not the case for u that leaves the

obstacle with a speed at least quadratic. It is what one observes well on the

two ﬁgures 2 and 3.

Example 2.

We consider in the 2-D case, the following problem, with Ω = ]−1, 1[

ψ = 0 and f as:

f(x, y) = 8x

+ 8y

− 1.

December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent

118

mu(x)

0 0.5 1 1.5

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1.1

Approched mu. With h = 1 / 256.

Exact mu.

Fig. 3. Comparison between µ and µ

for h = 1/256.

The solution to the obstacle problem is the function u deﬁned on Ω by:

(

u(x, y) =

(4x

+ 4y

− 1)

if 4x

+ 4y

− 1 ≤ 0,

u(x, y) = 0 if 4x

+ 4y

− 1 ≥ 0.

We solve the mixed problem for diﬀerent values of h, results obtained

seem to be in agreement with the established theoretical results.

Figures 4 and 5 represent respectively the isovalues of the functions u

and u

for h = 1/30. We can easily notice the strong similarities between

the two ﬁgures.

In the same manner Figures 6 and 7 represent respectively the isovalues

of exact µ and µ

, the approximation of µ. for h = 1/60, we notice also the

similarities of the two ﬁgures.

Figure 8 represents the H

(Ω)-error on u for diﬀerent values of h, one

can notice the linear aspect of this evolution, what conﬁrms the error esti-

mate of the theorem 3.1.

Finally, we note that 2-D simulations have been realized under the en-

vironment FreeFem++ .

Current and future developments

The aim of this work was to present a new mixed formulation of the obsta-

cle problem. We have proved that this formulation is as eﬀective as those

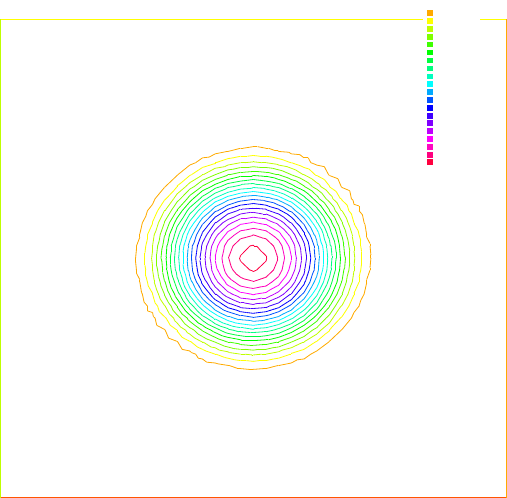
December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent

119

IsoValue

0.00078125

0.00234375

0.00390625

0.00546875

0.00703125

0.00859375

0.0101563

0.0117188

0.0132813

0.0148437

0.0164063

0.0179687

0.0195313

0.0210938

0.0226562

0.0242188

0.0257812

0.0273438

0.0289063

0.0304687

u exact 60x60

Fig. 4. Isovalues of exact u for h = 1/30.

classically known. Finally we have conﬁrmed the theoretical results that we

have established by numerical tests.

Finally we would like to conﬁrm that the approach we have presented

can be used successfully for other similar problems, in particular the bilat-

eral obstacle problem.

Acknowledgement

The authors would like to thank the anonymous referees for their interesting

remarks.

References

1. Kinderleher, D. Stampacchia. An introduction to variational inequalities and

their applications. Academic Press (1980).

2. A. Addou, E. B. Mermri. Sur une m´ethode de r´esolution d’un probl`eme

d’obstacle. Math-Recherche & Application n

◦

2, 59–69 (2000).

3. F. Brezzi & L. A. Caﬀarelli. Convergence of the discrete free boundaries for