Ammari H., Benkirane A., Touzani A. (editors) Recent Developments in Nonlinear Analysis
Подождите немного. Документ загружается.


December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent
120
IsoValue
0.000676368
0.00223902
0.00380167
0.00536432
0.00692697
0.00848962
0.0100523
0.0116149
0.0131776
0.0147402
0.0163029
0.0178655
0.0194282
0.0209908
0.0225535
0.0241161
0.0256788
0.0272414
0.0288041
0.0303667
uh 60x60
Fig. 5. Isovalues of u
h
for h = 1/30.
finite element approximations. R.A.I.R.O Numerical Analysis vol. 17, n
◦
4,
385–395 (1983).
4. Ricardo H. Nochetto. Sharp L
∞
-Error Estimates for semilinear Elliptic Prob-
lems with free boundaries. Numer. Maths. 54, 243-255 (1988).
5. R. Glowinski, J. L. Lions, R. Tr´emoli`eres. Analyse num´erique des in´equations
variationnelles Tome1. Dunod, Paris (1976).
6. F. Brezzi, W. W. Hagar. Error estimate for the finite element solution of
variational inequality, part II. Numer. Math. 31, 1–16 (1978).
7. Slimane, L; Bendali, A; Laborde, P. Mixed formulations for a class of vari-
ational inequalities. M2AN Math. Model. Numer. Anal. 38 (2004), no. 1,
177–201.
8. Degueil A. R´esolution par une m´ethode d’´el´ements finis d’un probl`eme de
STEPHAN en terme de temp´erature et en teneur en mat´eriau non gel´e. Th`ese
3
`eme
cycle, Bordeaux (1977).
9. I. Ekland, R. Temam. Analyse convexe et probl`emes variationnels. Dunod,
Paris (1974).
10. Slimane, L. M´ethodes mixtes et traitement du verrouillage num´erique pour la
r´esolution des in´equations variationnelles. Th`ese de l’Institut National des
Sciences Appliqu´ees, TOULOUSE (2001).
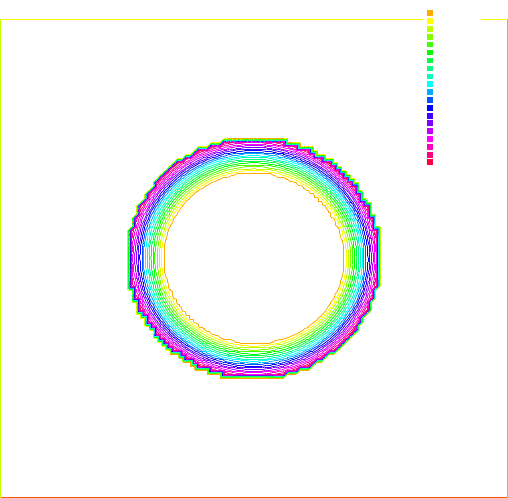
December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent
121
IsoValue
0.025
0.075
0.125
0.175
0.225
0.275
0.325
0.375
0.425
0.475
0.525
0.575
0.625
0.675
0.725
0.775
0.825
0.875
0.925
0.975
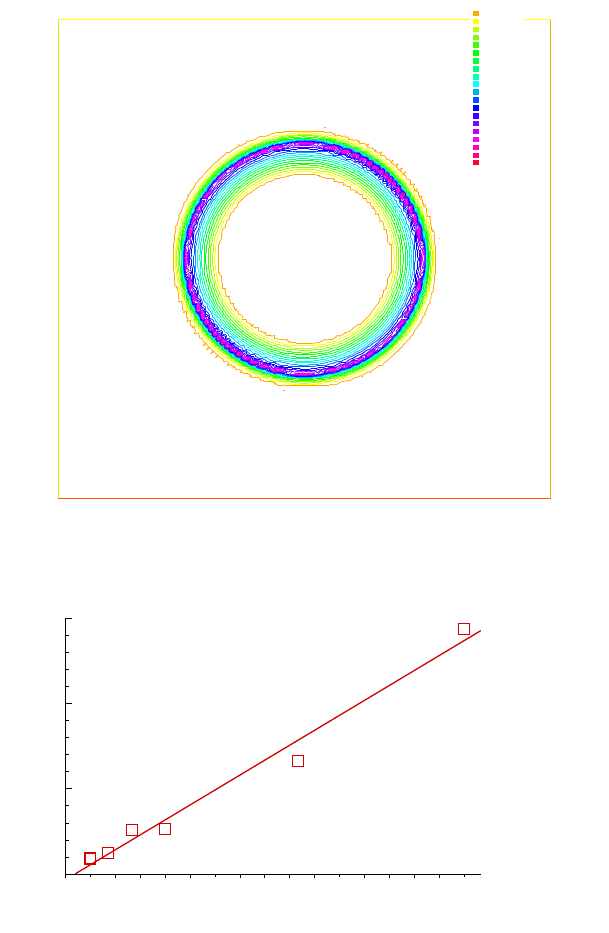
mu exact 120x120
Fig. 6. Isovalues of exact µ for h = 1/60.
11. P. G. Ciarlet. The Finite Element Method for Elliptic problems. Amsterdam:
North Holland, (1978).
12. P. A. Raviart, J. M. Thomas. Introduction l’analyse num´erique des ´equations
aux d´eriv´ees partielles. Masson, Paris (1992).
13. L. A. Caffarelli. The Obstacle Problem revisted. J. Fourier Anal. Appl. 4,
383–402 (1998).
14. F. Heicht, O. Pironneau, A. Le Hyaric, K. Ohtsuka. Freefem++. Lab-
oratoire Jacques-Louis Lions, Universit´e Pierre et Marie Curie, Paris,
(http://www.freefem.org/ff++).
December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent
122
IsoValue
0.0051434
0.0618342
0.118525
0.175216
0.231906
0.288597
0.345288
0.401979
0.458669
0.51536
0.572051
0.628742
0.685433
0.742123
0.798814
0.855505
0.912196
0.968886
1.02558
1.08227
muh 120x120
Fig. 7. Isovalues of µ
h
for h = 1/60.
h
H1-erroron u
0.05 0.1 0.15 0.2
0
0.005
0.01
0.015
Fig. 8. The H
1
0
(Ω)-error on u for different values of h.

December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent
123
An obstacle problem via a sequence of penalized problems
E. Azroul and M. Rhoudaf
D´epartement de Math´ematiques et Informatique
Facult´e des Sciences Dhar-Mahraz
B.P 1796 Atlas F`es, Morocco
In this paper, we shall concern with the existence result of unilateral parabolic
degenerated problems associated to the equations of the form
∂u
∂t
+ A(u) = f in Q
T
,
where A is a classical Leray-Lions operator acting from the weighted Sobolev
space L
p
(0, T, W
1,p
0
(Ω, w)) into its dual L
p
0
(0, T, W
−1,p
0
(Ω, w
∗
)), while the
datum f is assumed in L
1
(Q
T
).
The proof is based on the penalty methods.
Keywords: Unilateral parabolic degenerate problem; Existence result; Penalty
methods.
1. Introduction
In this paper, we investigate the problem of existence of solutions of the
obstacle problems associated to the following initial-boundary value prob-
lem:
(P
e
)
∂u
∂t
− div(a(x, t, u, ∇u)) = f in Q
T
= Ω ×(0, T )
u = 0 on Σ = ∂Ω × (0, T )
u(0) = u
0
in Ω,
where Ω is an open bounded subset of IR
N
, N ≥ 1, T > 0, and we have
set Q
T
the cylinder Ω × (0, T ) and Σ its lateral surface.
We assume that a(x, t, ξ) : Q
T
× IR
N
→ IR
N
is a Carath´eodry function
(i.e., measurable with respect to (x, t) and continuous with respect to ξ)
satisfying the hypotheses (H
2
) below.
The data are taken such that: f ∈ L
1
(Q
T
), u
0
∈ L
1
(Ω) and u
0
≥ 0.
More precisely, this paper deals with the existence of solution to the obstacle
December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent
124
degenerated parabolic problem (P
e
) in the sense of entropy solution:
(P
u
)
u ≥ ψ a.e. in Q
T
T
k
(u) ∈ L
p
(0, T, W
1,p
0
(Ω, w)), u ∈ C([0, T ], L
1
(Ω))
Z
Ω
S
k
(u −ϕ)(τ) dx +
Z
Q
τ
∂ϕ
∂t
T
k
(u −ϕ) dx dt
≤
Z
Q
τ
fT
k
(u −ϕ) dx dt +
Z
Ω
S
k
(u
0
− ϕ(x, 0)) dx
ϕ ∈ K
ψ
∩ L
∞
(Q
T
) ∩ C([0, T ], L
1
(Ω)) such that
∂ϕ
∂t
∈ L
p
0
(0, T, W
−1,p
0
(Ω, w
∗
)), ∀ k > 0
where S
k
(t) =
Z
t
0
T
k
(s) ds, ψ ∈ L
∞
(Ω) ∩ W
1,p
0
(Ω, w) and K
ψ
= {u ∈
L
p
(0, T, W
1,p
0
(Ω, w)), u ≥ ψ a.e. in Q
T
}.
The aim of our work is to investigate the relationship between the pos-
sibility to find solutions of (P ) by approximating the singular data f and
u
0
with sequences of regular functions. More precisely letting {f
} and u
0
be a standard approximation of f and u
0
(that is f
→ f in L
1
(Q) and
u
0
→ u
0
in L
1
(Ω)), and considering the approximate problem:
(P
e
)
∂u
∂t
− div(a(x, t, u
, ∇u
)) −
1
T
(u
− ψ)
−
= f
in Q
T
u
= 0 on Σ
u
(0) = u
0
in Ω.
We study the possibility to find a solution of (P
u
) as a limit of a subse-
quence {u
} of solutions of (P
e
).
The penalized term
1
T
(u
−ψ)
−
introduced in (P
e
) play a crucial role
in the proof of our main result, in particular this term allows to prove that
the solution u of (P
u
) belongs in K
ψ
(that is u ≥ ψ).
A priori estimates of the truncations T
k
(u
) are obtained in
L
p
(0, T, W
1,p
0
(Ω, w)). For the passage to the limit, we prove the strong
converge of the truncation of u
and the almost everywhere convergence
of ∇u
is proved. An example of operator model is,
A(u) = −div(|x|
r
|∇u|
p−2
∇u), r > 0.
In this context of parabolic problems, if w ≡ 1, existence results for (P
e
)
have been proved in
18
when f belongs to L
p
(0, T, W
−1,p
0
(Ω)) and u
0
is in
L
2
(Ω). The case where f belongs to L
1
(Q
T
) is investigated in [,
1920
] while
the case w 6= 1, is studied in [,
222
] where in the first work the authors have
studied the variational case (f ∈ L
p
0
(0, T, W
−1,p
0
(Ω, w
∗
)) and in the second
work the L
1
(Q
T
) case is treated.

December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent
125
Let us mention that in the literature of unilateral problems, the elliptic
case is more studied, while the study of parabolic case is poor.
2. Preliminaries and basic assumptions
Let Ω be a bounded open subset of IR
N
, p be a real number such that
1 < p < ∞ and w = {w
i
(x), 1 ≤ i ≤ N } be a vector of weight functions, i.e.,
every component w
i
(x) is a measurable function which is strictly positive
a.e. in Ω. Further, we suppose in all our considerations that, there exists
r
0
> max(N, p) such that w
r
0
r
0
−p
i
∈ L
1
loc
(Ω), (1)
and
w
−1
p−1
i
∈ L
1
loc
(Ω), (2)
for any 0 ≤ i ≤ N.
We denote by W
1,p
(Ω, w) the space of all real-valued functions u ∈
L
p
(Ω, w
0
) such that the derivatives in the sense of distributions fulfill
∂u
∂x
i
∈ L
p
(Ω, w
i
) for all i = 1, ..., N.
Which is a Banach space under the norm,
kuk
1,p,w
=
"
Z
Ω
|u(x)|
p
w
0
dx +
N
X
i=1
Z
Ω
|
∂u(x)
∂x
i
|
p
w
i
(x) dx
#
1
p
. (3)
The condition (1) implies that C
∞
0
(Ω) is a subset of W
1,p
(Ω, w) and con-
sequently, we can introduce the subspace W
1,p
0
(Ω, w) of W
1,p
(Ω, w) as the
closure of C
∞
0
(Ω) with respect to the norm (3). Moreover, the condition (2)
implies that W
1,p
(Ω, w) as well as W
1,p
0
(Ω, w) are reflexive Banach spaces.
We recall that the dual space of weighted Sobolev spaces W
1,p
0
(Ω, w) is
equivalent to W
−1,p
0
(Ω, w
∗
), where w
∗
= {w
∗
i
= w
1−p
0
i
, i = 0, ..., N} and
where p
0
is the conjugate of p, i.e., p
0
=
p
p−1
. For more details, we refer the
reader to.
12
Now we state the following assumptions:
Assumption (H
1
) For 2 ≤ p < ∞, we suppose that the expression
k|uk| =
N
X
i=1
Z
Ω
|
∂u
∂x
i
|
p
w
i
(x) dx
!
1
p
(4)

December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent
126
is a norm on W
1,p
0
(Ω, w) which is equivalent to (3) and that there exists a
weight function σ on Ω such that,
σ ∈ L
1
(Ω) and σ
−1
∈ L
1
(Ω). (5)
We assume also the Hardy inequality,
Z
Ω
|u(x)|
p
σ dx
1
p
≤ c
N
X
i=1
Z
Ω
|
∂u
∂x
i
|
p
w
i
(x) dx
!
1
p
, (6)
holds for every u ∈ W
1,p
0
(Ω, w) with a constant c > 0 independent of u.
Moreover, the imbedding
W
1,p
0
(Ω, w) ,→ L
p
(Ω, σ) (7)
expressed by the inequality (6) is compact.
Note that (W
1,p
0
(Ω, w), k|.k|) is a uniformly convex ( and thus reflexive)
Banach space.
Remark 2.1. Assume that w
0
(x) ≡ 1 and there exists ν ∈
N
P
, +∞
∩
h
1
P −1
, +∞
h
such that
w
N
N −1
i
, w
−ν
i
∈ L
1
(Ω) for all i = 1, ..., N. (8)
Note that the assumptions (1) and (8) imply that,
k|uk| =
N
X
i=1
Z
Ω
|
∂u
∂x
i
|
p
w
i
(x) dx
!
1
p
(9)
is a norm defined on W
1,p
0
(Ω, w) and its equivalent to (3) and that, the
imbedding
W
1,p
0
(Ω, w) ,→,→ L
p
(Ω) (10)
is compact [ see,
12
pp 46].
Thus the hypotheses (H
1
) is satisfied for σ ≡ 1.
Assumption (H
2
)
a(x, t, s, ξ).ξ ≥ α
N
X
i=1
w
i
|ξ
i
|
p
, (11)
where c
1
(x, t) is a positive function in L
p
0
(Q), and α, β are strictly positive
constants.
December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent
127
We recall that, for k > 1 and s in IR, the truncation is defined as
T
k
(s) =
(
s if |s| ≤ k
k
s
|s|
if |s| > k.
3. Some technical lemmas
3.1. Some functional properties of time-regularization of a
function u
In order to deal with time derivative, we introduce a time mollification of a
function u belonging in some weighted Lebesgue space. Thus we define for
all µ ≥ 0 and all (x, t) ∈ Q
T
,
u
µ
= µ
Z
t
−∞
˜u(x, s)exp(µ(s −t)) ds where ˜u(x, s) = u(x, s)χ
(0,T )
(s).
Proposition 3.1.
1) If u ∈ L
p
(Q
T
, w
i
), then, u
µ
is measurable in Q
T
,
∂u
µ
∂t
= µ(u −u
µ
) and
Z
Q
|u
µ
|
p
w
i
(x) dx dt
1
p
≤
Z
Q
|u|
p
w
i
(x) dx dt
1
p
,
i.e.,
ku
µ
k
L
p
(Q
T
,w
i
)
≤ kuk
L
p
(Q
T
,w
i
)
.
2) If u ∈ W
1,p
0
(Q
T
, w), then u
µ
→ u in W
1,p
0
(Q
T
, w) as µ → +∞.
3) If u
n
→ u in W
1,p
0
(Q
T
, w), then (u
n
)
µ
→ u
µ
in W
1,p
0
(Q
T
, w).
3.2. Some weighted imbedding and compactness results
In this section, we establish some imbedding and compactness results in
weighted Sobolev Spaces which allow in particular to extend in the settings
of weighted Sobolev spaces, some trace results and the Aubin’s and Simon’s
results
21
.
Let V = W
1,p
0
(Ω, w), H = L
2
(Ω, σ) and let V
∗
= W
−1,p
0
(Ω, w
∗
), with
(2 ≤ p < ∞).
Let X = L
p
(0, T, V ). The dual space of X is X
∗
= L
p
0
(0, T, V
∗
) where
1
p
0
+
1
p
= 1 and denoting the space W
1
p
(0, T, V, H) = {v ∈ X : v
0
∈ X
∗
}
endowed with the norm
kuk
w
1
p
= kuk
X
+ ku
0
k
X
∗
, (12)

December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent
128
which is a Banach space. Here u
0
stands for the generalized derivative of u,
i.e.,
Z
T
0
u
0
(t)ϕ(t) dt = −
Z
T
0
u(t)ϕ
0
(t) dt for all ϕ ∈ C
∞
0
(0, T ).
Lemma 3.1.
The Banach space H is an Hilbert space and its dual H
0
can be identified
with him self, i.e., H
0
' H.
Indeed, let
F : H × H → IR
(f, g) 7→
Z
Ω
fgσ dx.
Remark that F is a symmetric bilinear form, which is also continuous and
defined positively, since
Z
Ω
fgσ dx =
Z
Ω
fσ
1
2
gσ
1
2
dx ≤
Z
Ω
|f|
2
σ dx
1
2
Z
Ω
|g|
2
σ dx
1
2
.
Then, the Banach space H is an Hilbert space.
Finally by a standard argument, we can identified H with its dual H
0
i.e.,
H
0
' H.
Lemma 3.2.
2
The evolution triple V ⊆ H ⊆ V
∗
is verified.
Lemma 3.3.
2
Assume that,
∂u
n
∂t
= h
n
+ k
n
in D
0
(Ω),
where h
n
and k
n
are bounded respectively in L
p
0
(0, T, W
1,p
0
(Ω, w
∗
) and in
L
1
(Q
T
) .
If u
n
is bounded in L
p
(0, T, W
1,p
0
(Ω, w)), then u
n
→ u in L
p
loc
(Q
T
, σ).
Lemma 3.4.
2
Let g ∈ L
r
(Q
T
, γ) and let g
n
∈ L
r
(Q
T
, γ), with kg
n
k
L
r
(Q
T
,γ)
≤ c, 1 <
r < ∞. If g
n
(x) → g(x) a.e in Q
T
, then g
n
* g in L
r
(Q
T
, γ), where *
denotes weak convergence and γ is a weight function on Q
T
.
December 28, 2009 12:15 WSPC - Proceedings Trim Size: 9in x 6in recent
129
Lemma 3.5.
2
Assume that (H
1
) and (H
2
) are satisfied and let (u
n
) be a sequence in
L
p
(0, T, W
1,p
0
(Ω, w)) such that u
n
* u weakly in L
p
(0, T, W
1,p
0
(Ω, w)) and
Z
Q
[a(x, t, u
n
, ∇u
n
) − a(x, t, u
n
, ∇u)][∇u
n
− ∇u] dxdt → 0. (13)
Then, u
n
→ u in L
p
(0, T, W
1,p
0
(Ω, w)).
Lemma 3.6.
23
Let V ⊆ H ⊆ V
∗
be an evolution triple. Then the imbedding
W
1
p
(0, T, V, H) ,→ C([0, T ]), H)
is continuous .
3.3. Main results
Theorem 3.1. Let u
0
∈ L
1
(Ω) such that u
0
≥ 0. Assume that (H
1
) and
(H
2
) hold true. Then there exists at last one solution u ∈ C([0, T ]; L
1
(Ω))
such that u(x, 0) = u
0
a.e. and for all τ ∈]0, T ],
T
k
(u) ∈ L
p
(0, T, W
1,p
0
(Ω, w)), u ≥ ψ a.e. in Ω
Z
Ω
S
k
(u(τ) − ϕ(τ)) dx + h
∂ϕ
∂t
, T
k
(u −ϕ)i
Q
τ
+
Z
Q
τ
a(x, t, u, ∇u)∇T
k
(u −ϕ) dx dt
≤
Z
Q
τ
fT
k
(u −ϕ) dx dt +
Z
Ω
S
k
(u
0
− ϕ(x, 0)) dx
∀ k > 0 and ∀ ϕ ∈ K
ψ
∩L
∞
(Q) such that
∂ϕ
∂t
∈ L
p
0
(0, T, W
−1,p
0
(Ω, w
∗
)),
where Q
τ
= Ω×]0, τ[.
Proof.
Step 1: A priori estimates
Consider the approximate problem
(P
)
(
∂u
∂t
− div(a(x, t, u
, ∇u
)) −
1
T
1
(u
− ψ)
−
= f
u
∈ L
p
(0, T, W
1,p
0
(Ω, w)), u
(x, 0) = u
0
where f
→ f strongly L
1
(Q), u
0
→ u
0
strongly L
1
(Ω).
Thanks to,
2
there exists at least one solution of the problem (P
).
