Amaro A., Reed D., Soares P. (editors) Modelling Forest Systems

Подождите немного. Документ загружается.

19Amaro Forests - Chap 17 25/7/03 11:07 am Page 196

196 N.M. Tchebakova and E.I. Parfenova

< 25

25–50

50–75

75–100

100–125

125–150

(a) (b)

Fig. 17.7. Living phytomass (t/ha) of dark-needled forests across the study area under current (a) and a

warmed climate (b). NA means that a species is not available in a given pixel.

by succession stage. The phases of cedar and ﬁr forest successions caused by forest

ﬁres, droughts or insect pest outbreaks (Polikarpov, 1970) repeat in 200–250 years.

Forest gap models (Shugart, 1984) may be used to specify the forest composition of

these mixed cedar and ﬁr stands at different succession stages.

Acknowledgement

This study was supported by the Russian Foundation for Basic Sciences No.

02-04-49888.

References

Alexeyev, V.A. and Birdsey, R.A. (eds) (1998) Carbon Storage in Forests and Peatlands of Russia. USDA

Forest Service, Northeastern Research Station, General Technical Report NE-244, Radnor,

Pennsylvania, 137 pp.

Budyko, M.I. (1974) Climate and Life. Academic Press, New York, 508 pp.

Hulme, M. and Sheard, N. (1999) Climate Change Scenarios for the Russian Federation. Climatic

Research Unit, Norwich, 6 pp.

Nazimova, D.I. (1975) Mountain Dark-needled Forests of West Sayan Mountains. Nauka,

Leningrad, 120 pp.

Parfenova, E.I. and Tchebakova, N.M. (2000) Possible vegetation change in the Altai mountains

under climate warming. Geobotanical Mapping 1998–2000, 26–31.

Polikarpov, N.P. (1970) Complex investigations in mountain forests of West Sayan. In: Zhukov,

A.B. (ed.) Questions of Forestry, Vol. 1. Institute of Forestry, Krasnoyarsk, pp. 26–79.

Polikarpov, N.P., Tchebakova, N.M. and Nazimova, D.I. (1986) Climate and Mountain Forests of

Southern Siberia. Nauka, Novosibirsk, 225 pp.

Reference Books on Climate of the USSR (1964–1970) Issues: 17, 20–24. Gidrometeoizdat,

Leningrad.

19Amaro Forests - Chap 17 25/7/03 11:07 am Page 197

197 Stand Growth and Productivity in a Changing Climate

Savina, L.N. (1986) Bor

eal Forests of Northern Asia during the Holocene. Nauka, Novosibirsk, 192

pp.

Semechkin, I.V., Popova, Y.M. and Popov, V.E. (1985) Stand structure and productivity. In:

Isaev, A.S. (ed.) Pinus sibirica Forests of Siberia. Nauka, Novosibirsk, pp. 117–132.

Shugart, H. (1984) A Theory of Forest Dynamics: the Ecological Implications of Forest Succession

Models. Springer, New York, 278 pp.

Shumilova, L.V. (1962) Botanical Geography of Siberia. Tomsk University Press, Tomsk, 440 pp.

Smagin, V.N., Ilinskaya, S.A., Nazimova, D.I., Novoseltseva, I.F. and Cherednikova, J.S. (1980)

In: Smagin, B.N. (ed.) Forest Types of Mountains of Southern Siberia. Nauka, Novosibirsk,

234 pp.

Tchebakova, N.M., Monserud, R.A. and Leemans, R. (1994) A Siberian vegetation model based

on climatic parameters. Canadian Journal of Forest Research 24, 1597–1607.

19Amaro Forests - Chap 17 25/7/03 11:07 am Page 198

20Amaro Forests Part 3 25/7/03 11:07 am Page 199

Part 3

Estimation Processes

Parameter estimation is required prior to the building of a mathematical code that will be

used by researchers, forest practitioners and managers, or decision makers and policy mak-

ers. Parameter estimates are necessary for process, empirical and hybrid models.

Data quality is a key issue affecting the prospective quality of the model. The sources of

variability are related to the language communication process (the so-called linguistic vari-

ability), the intrinsic variability (intrinsic to the variable that is being measured) and the mea-

surement variability (due to the measurement method).

Before estimating parameters, there are several decisions on data type and data structures

(e.g. dependent and independent, re-measurements, independent, time and spatial series,

class and continuous, and expert knowledge) and the estimation methods that may be used

(e.g. qualitative (expert and literature), moments, maximum likelihood, marginal quasi-

likelihood, penalized quasi-likelihood, parameter recovery, parameter prediction, percentile,

Markov chains, OLS and NOLS, generalized OLS and NOLS, mixed linear and non-linear,

SUR and NSUR, 2SLS and N2SLS, 3SLS and N3SLS, generalized methods, neural networks,

geostatistical and Bayesian techniques).

After parameter estimation and model construction, the next step consists of the process

of verifying the model. The use of simple or more complex tools in order to verify the statisti-

cal assumptions and the evaluation is essential to test the model’s adherence to reality and

the coherency of its results. A very important contribution to this process is the analysis of the

biological interpretation of the parameters.

Parameter estimation is a dynamic task: reality is changing and the knowledge of the real-

ity is also changing. All the priority research topics in this area have the same objective:

reducing uncertainty in the ultimate model predictions.

The possibility of building web-based learning tools draws attention to the fact that many

of the scientiﬁc papers submitted for publication are often not very clear, or even difﬁcult to

understand, especially with regard to parameter estimation. To understand the process it is

often necessary to reproduce the methodology, and that can be difﬁcult in many cases. The

availability of a learning tool with some training examples and subsets of the original data,

along with a more in-depth explanation of the methods used, could help in understanding the

methods used and provide additional information that would certainly improve and validate

the proposed procedures.

An existing model needs some updating – after some time it will need to be re-evaluated

and modiﬁed: knowledge of the system evolves and the tr

ue situation may change. To

accomplish this task, there are two main possibilities: (i) to start from the beginning (adding

199

20Amaro Forests Part 3 25/7/03 11:07 am Page 200

200 Part 3

new data, re-evaluating the possibility of having new functional forms, new structures, new

methods), or (ii) to develop and use tools to support model updating. Control engineers use

variants of the Kalman ﬁlter to update the state of a system in real time, for example. As

process measurements are recorded, they are optimally combined with model predictions in

the ﬁlter update step. Such techniques were developed for real-time systems (i.e. short time

steps) and may be very appropriate in process modelling. However, for traditional long-term

growth modelling, the beneﬁt of applying such techniques is questionable when there may

be years between measurements. In the intervening time, it may be more efﬁcient to re-ﬁt the

existing model, develop a completely new model, or use newly developed estimation tech-

niques on existing model forms that were not known at the last calibration.

Tree mortality is one of the key processes in forest ecosystems. It has been modelled tradi-

tionally with logistic regression using the maximum likelihood estimation method. It is com-

mon for individual tree mortality data to include observations from several stands with more

than one mortality tree per stand. As a consequence, the observations (trees in the same

stand) are correlated. Ignoring data structure in mortality data leads to several consequences,

such as underestimation of standard errors for higher-level ﬁxed effects. The generalized lin-

ear mixed models are useful when data are not normally distributed or have been hierarchi-

cally collected. Methods of analysis and measures of model ﬁt appropriate to use in these

situations should be seriously considered.

The quasi-likelihood estimation method used in generalized linear mixed models is

known for its ability to produce efﬁcient estimates without exact information about the likeli-

hood function. Both marginal quasi-likelihood (MQL) and penalized quasi-likelihood (PQL)

estimation methods have been used. The quasi-likelihood methods are attractive because

they are available in commonly used software. However, one should be aware of the possible

limitations of these methods, e.g. in estimation, the often small number of observations at dif-

ferent levels may cause bias in the resulting estimates.

Multi-level mortality models can be improved by: (i) increasing data and variables in the

model; (ii) estimating the mortality model simultaneously with the growth model; and (iii)

developing goodness-of-ﬁt measures in the case of generalized linear mixed models. Increasing

information by obtaining more data can often be done, but it may be difﬁcult to determine what

level is needed. There are often unmeasured variables affecting tree mortality, and inclusion of

this information can often improve the mortality model. However, if the number of variables

increases, the model becomes more complex. The most recently developed mortality models

often have the same independent variables used to describe tree vitality. To improve model esti-

mates, the growth and mortality models may be estimated simultaneously so that the mortality

curve asymptotically approaches the forest self-thinning limit. Developing goodness-of-ﬁt mea-

sures in the case of correlated data is an issue that must be considered in the future.

Modelling methods are commonly assessed based on their properties of unbiasedness,

asymptotic unbiasedness, consistency and efﬁciency (as related to a standard). They are also

assessed as to their ability to hold properties under different types and distributions of data.

Properties of ﬁtting methods are affected by several variables, including sample size, the num-

ber of parameters to be estimated, the distribution of the model errors and the ﬁtting method.

Some techniques only have desirable (usually asymptotic) properties for very large sample

sizes, and may function poorly with small sample sizes. Often, techniques that are based on the

normal distribution of model errors give good results for small samples when the model errors

are indeed normal. For non-normal distributions when the distribution is known, maximum

likelihood estimators give ‘good’ results. However, for very large numbers of parameters to be

estimated, methods requiring search algorithms may become unstable, resulting in local min-

ima, and may show large variations in parameter estimates for different sample data sets.

The following contributions examine these and other issues related to parameter estima-

tion in forest models. The editors wish to acknowledge the efforts of Ana Amaro (Portugal)

and Jeffrey Gove (USA) for coordinating this section, and thank them for their contributions

to this volume.

21Amaro Forests - Chap 18 1/8/03 11:53 am Page 201

18 Estimation and Applications of

Size-biased Distributions in

Forestry

Jeffrey H. Gove

Abstract

Size-biased distributions arise naturally in several contexts in forestry and ecology. Simple

power relationships (e.g. basal area and diameter at breast height) between variables are one

such area of interest arising from a modelling perspective. Another, probability proportional to

size (PPS) sampling, is found in the most widely used methods for sampling standing or dead

and fallen material in the forest. Often it is desirable or necessary to estimate a parametric

probability density model based on size-biased data. Traditional equal probability methods

may not be appropriate, or may be less efﬁcient in such circumstances, and estimation is better

conducted utilizing size-biased theory. This chapter surveys some of the possible uses of size-

biased distribution theory in forestry and related ﬁelds.

Introduction

Size-biased distributions are a special case of the more general form known as

weighted distributions. First introduced by Fisher (1934) to model ascertainment

bias, weighted distributions were later formalized in a unifying theory by Rao

(1965). Such distributions arise naturally in practice when observations from a sam-

ple are recorded with unequal probability, such as from probability proportional to

size (PPS) designs. Brieﬂy, if the random variable X has distribution f(x;

), with

unknown parameters

, then the corresponding weighted distribution is of the form

fx;

)

wx f x ;

)

(

()(

[

()

]

where w(x) is a non-negative weight function such that E[w(x)] exists.

A special case of interest arises when the weight function is of the form w

(x) =

. Such distributions are known as size-biased distributions of order α and are

written as (Patil and Ord, 1976; Patil, 1981; Mahfoud and Patil, 1982):

USDA Forest Service, Northeastern Research Station, USA

Correspondence to: jhgove@christa.unh.edu or jgove@fs.fed.us

21Amaro Forests - Chap 18 1/8/03 11:53 am Page 202



202 J.H. Gove

(

fx;

)

xf x ;

)

(1)

(

where

 = x

f(x;

) dx is the αth raw moment of f(x;

). Denote X the original, or

equal probability, random variable, and X

(x;

) the size-biased random variable.

α α

The most common cases of size-biased distributions occur when α=1 or 2; in the

context of sampling, these special cases may be termed length- and area-biased,

respectively.

Weighted distributions have numerous applications in forestry and ecology.

arren (1975) was the ﬁrst to apply them in connection with sampling wood

cells. Van Deusen (1986) arrived at size-biased distribution theory independently

and applied it to ﬁtting distributions of diameter at breast height (DBH) data aris-

ing from horizontal point sampling (HPS) (Grosenbaugh, 1958) inventories.

Subsequently, Lappi and Bailey (1987) used weighted distributions to analyse

HPS diameter increment data. More recently, weighted distributions were used

by Magnussen et al. (1999) to recover the distribution of canopy heights from air-

borne laser scanner measurements. In ecology, Dennis and Patil (1984) use sto-

chastic differential equations to arrive at a weighted gamma distribution as the

stationary probability density function (PDF) for a stochastic population model

with predation effects. In ﬁsheries, Taillie et al. (1995) modelled populations of

ﬁsh stocks using weighted distributions. In these last two examples, weighted

distributions were not directly tied to the underlying sample selection method,

but were simply convenient models for the observed data. Recognizing the fact

that weighted distributions may be applied as convenient PDF models, Gove and

Patil (1998) developed a compatible theory, unifying the DBH–frequency and

basal area–DBH distributions based on the quadratic relationship between diam-

eter and basal area. Lastly, Gove (2000) extended the work of Van Deusen (1986)

by providing simulation experiments and guidelines for ﬁtting size-biased distri-

butions to data.

The purpose of this chapter is to review some of the more recent results on size-

biased distributions pertaining to parameter estimation in for

estry, with special

emphasis on the Weibull family. In addition, some new results and avenues for pos-

sible future research will be presented. Finally, a new computer program with

graphical user interface (GUI) developed by the author for ﬁtting size-biased

Weibull distributions will be brieﬂy discussed.

Size-biased Weibull Distributions

Weibull distributions have found widespread use in forestry for modelling since

they were ﬁrst introduced by Bailey and Dell (1973). The two- and three-parameter

Weibull PDFs are given as

fx;

)





 



−1

−

(

)

x0

 

(



 





−1

)

(



 





−

(

x−

ξβ

)

 

fx;

)





 

x −



e x

with

= (

) and

= (

), respectively. The unknown parameters

> 0,

> 0 and

> 0 are the shape, scale and location parameters to be estimated for a given sample

of data.

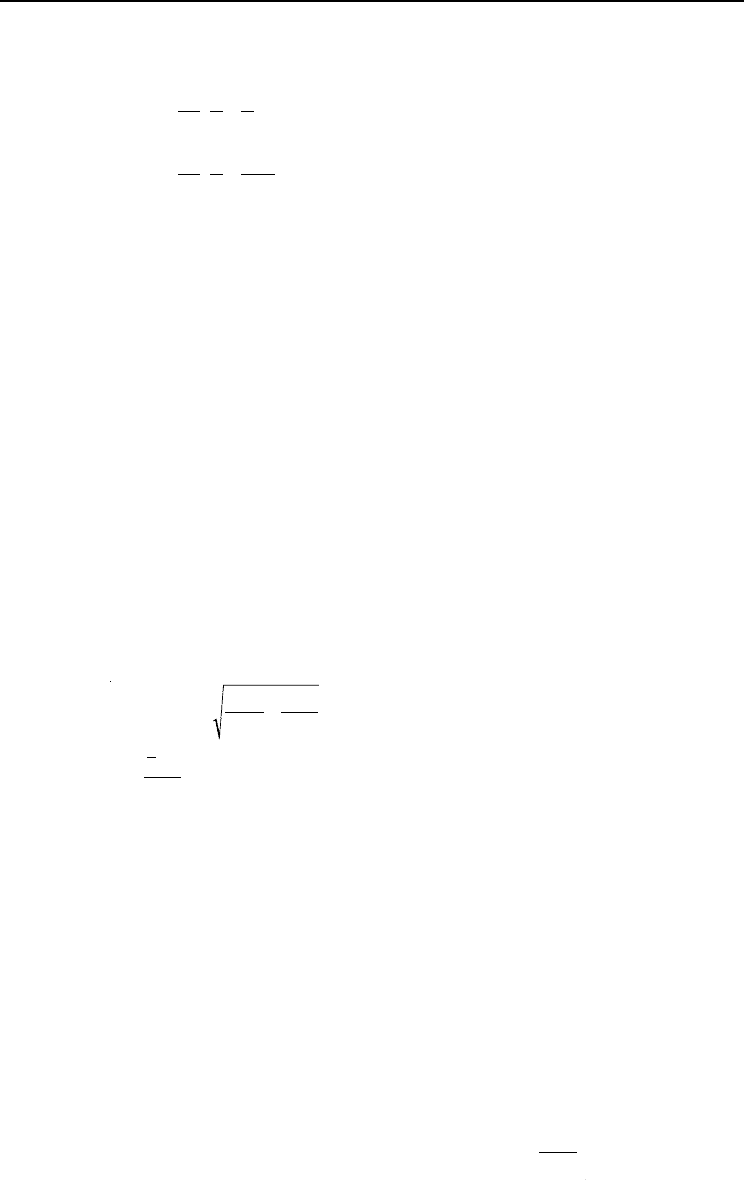
21Amaro Forests - Chap 18 1/8/03 11:53 am Page 203



203 Size-biased Distributions in Forestry

These PDFs can be easily converted to their size-biased counterparts using

Equation 1, namely



 



−1

fx;

)



 





−

(

)

x0

(



  

(



 

x −



−1

−

(

x−

ξβ

)

fx;

)



 





e x

  

for the two- and three-parameter versions, respectively, with the same restrictions

on the parameters as for the equal probability PDFs. Gove and Patil (1998) have

also shown that the size-biased two-parameter Weibull can be transformed,

through change-of-variables techniques, to the standard gamma distribution. Such

a transformation may be advantageous for simulation studies. For example, Gove

(2000) used the standard gamma to draw probability-weighted samples to simulate

the HPS tally distribution.

Because of their popularity in modelling the traditional DBH–frequency distri-

bution, both the two- and thr

ee-parameter size-biased Weibull PDFs are appropriate

as candidate probability models in all of the applications presented in this chapter.

Size-biased Weibulls: Moment Estimation

Size-biased two-parameter Weibull moment estimators

The development of moment estimators for the size-biased two-parameter Weibull

distribution is given in Gove (2003a). Ther

e, a modiﬁed moment estimation scheme

along the lines of Cohen (1965), using the coefﬁcient of variation, is presented. Let

and

represent the moment estimates for the shape and scale parameters, respec-

tively; then the moment equations are

= ΓΓ

−1

−

(2)

αα

x Γ

(3)

where x¯ and

CV are the sample mean and coefﬁcient of variation, respectively, with

= Γ(

+ 1), Γ

=Γ(

+ 1) and Γ(k)=

∝

k1

x

dx, k > 0, the gamma function.

Equation 2 is solved iteratively for the shape parameter, then the scale parameter

can be found directly by substitution into Equation 3.

Size-biased three-parameter Weibull moment estimators

Unfortunately, the moment equations for the size-biased three-parameter Weibull

e not easily couched in a modiﬁed scheme like that for the two-parameter where

the coefﬁcient of variation can be used. Thus, the moment equations for the ﬁrst

three raw moments are used; these moments can be built up from the moments of

∗

the equal probability three-parameter Weibull (Gove 2003a). Let

∗



= d

(x,

)dx

denote the

th raw moment of the size-biased three-parameter Weibull distribution

of order α. Then, it is straightforward to show that

αζ

′

Now, since

=1 or

αζ

′

21Amaro Forests - Chap 18 1/8/03 11:53 am Page 204



204 J.H. Gove

2 for the most common forestry applications, and ζ = 1,...,3 for the ﬁrst three raw

moments, it is easy to see from the numerator of

∗



that the ﬁrst ﬁve raw moments

of the three-parameter Weibull distribution are required for the estimating equa-

tions. The moments for the three-parameter Weibull are of the form









−1









−2

…

(4)

α α

−1





−2





where the coefﬁcients (

), i = 1,...,

follow Pascal’s triangle. Thus, for example, the

*

second raw moment from a length-biased three-parameter Weibull,

1,2

3 2 3



+ 3

β ξ ξ

It should be clear that the moment equations for the length- and area-biased ver-

sions differ. For comparison, the second raw moment from an area-biased three-

*

parameter Weibull is given as

, and is therefore more complicated:

4 3

2 2 3



+ 4

+ 6

+ 4

β ξ ξ



+ 2

β ξ ξ

The ﬁrst three moment equations are set equal to the ﬁrst three sample

moments and solved simultaneously for the estimates

˜ ˜

. Further details are

given in Gove (2003a,c).

Size-biased Weibulls: Maximum Likelihood Estimation

The maximum likelihood estimators (MLEs) for size-biased Weibulls can be found

by building up from the equal probability likelihood, just as in the case of the three-

parameter moment estimators in the previous section. The equal probability three-

parameter Weibull log-likelihood is

n n

ln L = nln









(

− 1

)

∑

(

−

)

−

∑

(

−

)





i=1 i=1

and the two-parameter log-likelihood follows directly by setting ξ = 0.

The size-biased form was ﬁrst given by Van Deusen (1986), where he noted that

it was composed of the equal pr

obability log-likelihood plus a constant and a correc-

tion term. He also noted that the purpose of the correction was to account for the

fact that the observations are drawn with unequal probability. The general form of

the size-biased log-likelihood is given as

ln * = ln +

∑

ln x − nln

′

L L

i=1

where the second term is constant, depending only on the data, and thus may be

dropped if desired.

In addition, the gradient vector and Hessian matrix of ﬁrst- and second-order

partial derivatives ar

e also of the same form (Gove 2003a). For example, the gradient

∂ln L *

∂ln L

− n

ρα

()

∂

∂ln L *

∂ln L

− n

ρα

equations for the size-biased three-parameter Weibull follow the form

()

∂

∂ln L *

∂ln L

− n

ρα

()

∂

21Amaro Forests - Chap 18 1/8/03 11:53 am Page 205

205 Size-biased Distributions in Forestry

Notice that the correction term (n

(α )) depends on the size-biased order α . Thus,

there are unique corrections associated with length- and area-biased log-

likelihoods. The Hessian matrix follows the same pattern, being composed of the

equal probability and correction components. Detailed equations for the three-para-

meter gradient and Hessian are presented in Gove (2003a). In the two-parameter

size-biased Weibull, the equations are much simpler, due to the simpler nature of

the raw moment



in that distribution. The gradient equations for the two-parame-

ter case are given in Gove (2000).

The Basal Area-size Distribution

As mentioned earlier, the basal area-size distribution (BASD) is the size-biased dis-

tribution of order α = 2 of the traditional DBH–frequency distribution (Gove and

Patil, 1998). The relationship can easily be shown algebraically and arises, not from

sampling theory, but purely from the quadratic relationship between DBH and basal

area. If the random variable X is tree diameter, then X

∼ƒ

( x;

) is the DBH–frequency

distribution. From it, we normally calculate the number of trees in the ith diameter

class (N

), once the parameters

have been estimated from sample data

= N

(

)

(5)

∫

where x

and x are the lower and upper diameter class limits, respectively, and N is

the total number of trees per hectare.

The BASD comes about by redistributing the probability mass in terms of

basal ar

ea, rather than tree frequency. The random variable in both cases is still

DBH. The BASD can then be used to calculate the basal area (B

) in the ith DBH

class as

= B

∫

(

)

where B is the stand basal area per hectare. Thus, X

∼ƒ

(x;

Gove and Patil (1998) presented several examples of stands ﬁtted with a para-

meter r

ecovery model, all with the same basal area and number of trees, but span-

ning a wide range of the two-parameter Weibull parameter space. As an example,

the stand in their Figure 1d has been re-ﬁtted with a three-parameter Weibull model

and is presented in Fig. 18.1. This ﬁgure shows the empirical histogram for the

DBH–frequency distribution along with the Weibull curve ﬁtted by ML. Also shown

is the corresponding BASD curve, which shares the same estimated parameter vec-

tor

from ML.

Estimation of Weibull Parameters under Size-biased Sampling

Arguably, the two most useful forms of size-biased distributions arising in forestry

are the length- and area-biased models. Length-biased data arise from line intersect

samples (LIS) (Kaiser, 1983), horizontal and vertical line samples (HLS, VLS)

(Grosenbaugh, 1958) and transect relascope sampling (TRS) (Ståhl, 1998). Area-

biased data arise naturally from HPS and vertical point sampling (VPS)

(Grosenbaugh, 1958), and from point relascope sampling (PRS) (Gove et al., 1999) for

coarse woody debris. In this section these links are explored in more detail, with

special emphasis on the distribution of HPS tally tree diameters.