Amaro A., Reed D., Soares P. (editors) Modelling Forest Systems

Подождите немного. Документ загружается.

17Amaro Forests - Chap 15 25/7/03 1:54 pm Page 176

176 A. Kiviste et al.

The coefﬁcient of determination R

= 0.66 and the RMSE = 0.71 cm.

Using the moments method (Scolforo and Thierschi, 1998), the parameters of

Johnson’s S

B distribution can be predicted as follows:

= 0.7 MIN

λ = MAX

⋅−

)





(

= +⋅



− 8



(



s 4



⋅−

)

 



−



−1

γδ

=⋅







0 5















where

d −

STD

s =

MAX

d = arithmetic mean diameter

Height–diameter relationships

To date, a total of 28,441 sample trees with height–diameter measurements have

been r

ecorded in the database of the Estonian permanent plot network. Records

were classiﬁed into groups by storeys and species, and only the groups containing

at least 25 trees were used for the modelling of height–diameter relationships. As a

result, a total of 14,821 height–diameter measurements from 292 stands were used in

the analysis of height–diameter models.

On the basis of sample tree data, parameters H and b of the Nilsons’

height–diameter equation wer

e calculated for each stand using the system of linear

equations. The residual standard error of the model was 1.36 m.

The scale parameter H of the model expr

esses the mean height of the stand cor-

responding to the quadratic mean diameter. The shape parameter b characterizes the

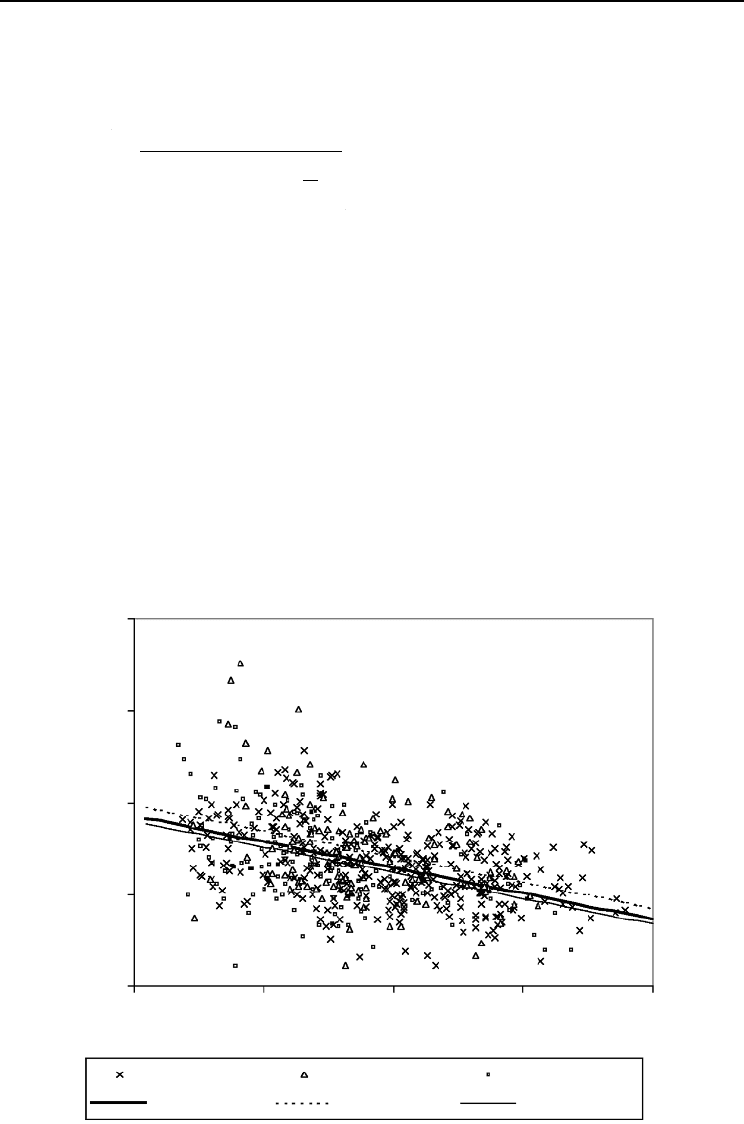
curvature of the height–diameter relationship (Fig. 15.4). Analysis of the estimates of

Relative height h/H

1.6

1.4

1.2

1.0

0.8

0.6

0.4

0.2

0.0

0.0 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8 2.0

Relative diameter d/

b = 0.05 b = 0.1 b = 0.2 b = 0.4

Fig. 15.4. Standardized height–diameter curves by Nilson’s (1999) model for different values of shape

parameter b.

17Amaro Forests - Chap 15 25/7/03 1:54 pm Page 177

177 Diameter Distribution Models

the shape parameter b

to the quadratic mean diameter D

parameter b b = a D, we get a one-parameter

height–diameter model:

h d a is a con-

c is a constant

H is the mean height

Discussion and Conclusions

a D

−− ⋅

( )

⋅−

























1 1.

0.8

0.6

0.4

0.2

Parameter b

Birch

0.359–0.0056D

Spruce

0.394–0.0056D

Pine

0.369–0.0056D

Quadratic mean diameter D (cm)

using Estonian growth plot data revealed a linear relationship

and the tree species (Fig. 15.5). By replacing the

with the linear relationship – 0.0056·

where is the tree height (m), is the tree breast height diameter (cm),

stant (0.369 for pine, 0.394 for spruce and 0.359 for other species),

(1.31 for pine, 1.47 for spruce and 1.38 for other species), and

parameter (corresponding to the quadratic mean diameter).

The residual standard error of the model was 1.50 m.

The creation of a network of permanent forest growth plots has been started in

Estonia. The network is designed for long-term observations of trees to be used for

building forest growth models for Estonia.

Numbering of trees with metallic tags or colour is a common practice in forest

permanent sample plots. We preferred the measurement of tree coordinates instead.

Re-measuring of almost 200 plots convinced us that the precision of the measure-

ments of azimuth and distance from plot centre was sufﬁcient to ensure quick loca-

tion of the same trees 5 years later. The additional advantage of measuring of tree

0 0056

10 20 30 40

Fig. 15.5. Relationship between parameter b and quadratic mean diameter D on the basis of ﬁrst-storey tree

data.

17Amaro Forests - Chap 15 25/7/03 1:54 pm Page 178

178 A. Kiviste et al.

coordinates is the availability of data for the construction of distance-dependent tree

growth models.

The establishment and maintenance of the network is an ongoing process.

Nevertheless, a considerable amount of data that can be used for modelling the for-

est str

ucture has already been collected.

The Johnson’s SB distribution was ﬂexible enough to describe diameter distribu-

tions of Estonian for

ests. Regression methods of parameter estimation represented a

better ﬁt than percentile methods. A diameter distribution model, the parameters of

which were predicted by stand variables, has been developed for Estonian forests.

Using the diameter distribution model, the parameters of which were predicted

by stand variables, 9% of the plots did not pass the Kolmogor

ov–Smirnov goodness-

of-ﬁt test. When distribution parameters were estimated using empirical diameter

distribution (using the moments method), then all the plots passed the

Kolmogorov–Smirnov goodness-of-ﬁt test. Thus, we did not manage to predict the

distribution parameters perfectly. It is likely that regular correlations between distri-

bution parameters and stand variables can be found in unmanaged forests; how-

ever, since thinning of stands is common practice in Estonia, it is unlikely that

perfect predictions of diameter distributions can be made.

A standardized height–diameter equation has been created for Estonian forests.

Depending on the number of height–diameter measur

ements, the equation can be

used as a one-parameter or two-parameter model. Model parameters can be esti-

mated by solving a system of linear equations.

For the height–diameter models, the values of parameter c wer

e estimated

according to main species. For this a data set was generated using Kuliesˇis’ (1993)

model for Lithuanian forests.

Residuals of the models were studied, and no signiﬁcant effect of tree diameter,

quadratic mean diameter or tr

ee species was found either for the two-parameter or for

the one-parameter model. However, a dependency of residuals on relative diameter

d/D was found in the Estonian forest plot data. Therefore, further correction of the

parameter c estimates is needed. Also, we cannot rule out additional dependence of the

values of parameters b and c on stand age, stocking grade, management history and

other stand variables.

Acknowledgement

This study was supported by the Estonian Science Foundation, Grant No. 4813.

References

Bowman, K.O. and Shenton, L.R. (1983) Johnson’s system of distributions. In: Encyclopedia of

Statistical Sciences, Vol. 4. John Wiley & Sons, New York, pp. 303–314.

Curtis, R.O. (1983) Procedures for Establishing and Maintaining Permanent Plots for Silvicultural

and Yield Research. USDA General Technical Report PNW-155, 56 pp.

Gustavsen, H.G., Roiko-Jokela, P. and Varmola, M. (1988) Kivennäismaiden talousmetsien pysyvat

(INKA ja TINKA) kokeet. Suunnitelmat, mittausmenetelmät ja aineistojen rakenteet.

Metsäntutkimuslaitoksen tiedonantoja 292, 212 pp. [in Finnish].

Hägglund, B. (1981) Forecasting Growth and Yield in Established Forests: an Outline and Analysis of

Outcome of a Subprogram Within Hugin Project. Swedish Univerity of Agricultural Sciences,

Department of Forest Survey, Report 31, 145 pp.

Hökka, H. (1997) Models for Predicting Growth and Yield in Drained Peatland Stands in Finland.

Finnish Forest Research Institute, Research Paper 651, 45 pp.

17Amaro Forests - Chap 15 25/7/03 1:54 pm Page 179

179 Diameter Distribution Models

Huang, S., Price, D. and Titus, S.J. (2000) Development of ecoregion-based height–diameter

models for white spr

uce in boreal forests. Forest Ecology and Management 129, 125–141.

Hynynen, J., Ojansuu, R., Hökka, H., Siipilehto, J., Salminen, H. and Haapala, P. (2002) Models

for Predicting Stand Development in MELA System. Finnish Forest Research Institute,

Research Paper 835, 116 pp.

Johnson, N.L. (1949) Systems of frequency curves generated by methods of translation.

Biometrika 36, 149–176.

Kamziah, A.K., Ahmad, M.I. and Lapongan, J. (1999) Nonlinear regression approach to esti-

mating Johnson SB parameters for diameter data. Canadian Journal of Forest Research 29,

310–314.

Knoebel, B.R. and Burkhart, H.E. (1991) A bivariate approach to modelling forest diameter dis-

tributions at two points in time. Biometrics 47, 241–253.

Kuliesˇis, A. (1993) Lietuvos medynu prieaugio ir jo panaudojimo normatyvai. Kaunas, 383 pp. [in

Lithuanian].

Mängel, M. (2000) Puu ko˜rguse ja diameetri vahelise seose modelleerimine proovitükkide andmeil.

EPMÜ metsakorralduse instituut. Lo˜putöö, 40 pp. [in Estonian].

Nilson, A. (1999) Pidev metsakorraldus – mis see on. In: Pidev Metsakorraldus. EPMÜ

Metsandusteaduskonna toimetised 32, 4–13 [in Estonian].

SAS Institute (1989) SAS/STAT User’s Guide, Version 6, 4th edn, Vol. 2, SAS Institute, Cary,

North Carolina, 846 pp.

Scolforo, J.R.S. and Thierschi, A. (1998) Estimativas e testes da distribuição de frequência

diâmétrica para Eucalyptus camaldulensis, através da distribuição Sb, por diferentes méto-

dos de ajuste. Scientia Forestalis 54, 93–106.

Slifker, J.F. and Shapiro, S.S. (1980) The Johnson System: selection and parameter estimation.

Technometrics 22, 239–246.

Estonian Forest Survey (1999) Centre Instruction of National Forest Inventory Fieldworks. 55 pp.

Tarve, T. (1986) Puude rinnasdiameetri jaotus Rakvere metsamajandi puistutes. EPA metsakorral-

duse kateeder, 36 pp. [in Estonian].

Zar, J.H. (1999) Biostatistical Analysis. Prentice-Hall, Upper Saddle River, New Jersey, 663 pp.

Zhou, B. and McTague, J.P. (1996) Comparsion and evaluation of ﬁve methods of the Johnson

System parameters. Canadian Journal of Forest Research 26, 928–935.

17Amaro Forests - Chap 15 25/7/03 1:54 pm Page 180

18Amaro Forests - Chap 16 1/8/03 11:53 am Page 181

16 Modelling the Diameter at Breast

Height Growth of Populus 

euramericana Plantations in Spain

Francisco Rodríguez,

José Antonio De la Rosa

and

Álvaro Aunós

Abstract

Preliminary results are presented in order to model the diameter at breast height growth of

three clones of Populus × euramericana (I-214, Luisa Avanzo and MC) in the Cinca valley

(Huesca, Spain) using data from re-measured permanent and measured temporary plots. The

model employed was an integral form of the Chapman–Richards equation with a reference age

established at 7 years. We built an anamorphic system of curves with different productivity

indexes (PIs), elaborating an empirical height–diameter relationship to estimate average height

based on a multiplicative model adapted by Cunia (1979).

Introduction

The hybrid poplar (Populus × euramericana) is a tree species of great economic impor-

tance in Spain, forming the basis of the peeler wood industry. According to the

Spanish Agriculture Department (Padró, 1992), poplar plantations occupy about

100,000 ha of forested area in Spain. Recently, these plantations have undergone a

remarkable expansion in areas such as the Cinca valley (Huesca province, northern

Spain), in which the hybrid clones I-214, Luisa Avanzo and MC are extensively

planted. This increase in forest land can be explained by two factors: (i) its rapid

growth and, (ii) its suitability for vegetative reproduction (Rueda et al., 1997).

Nowadays, poplars can be used as an alternative to less proﬁtable agricultural

crops, partly due to the new orientations of the EU agrarian policies favouring the

reforestation of former agricultural land. However, despite the many hectares cur-

rently dedicated to poplars, more than 750,000 m

of wood is imported annually to

Spain.

One of the major concerns of forest managers in poplar plantations is related to

the possibility of pr

edicting the production of peeler wood in the future. This is also

critical in evaluating the sustainability of forest management practices within the

framework of the national forest policies. In this context, development of growth

models for the species represents a useful tool.

University of Lleida, UdL-ETSEA, Spain

Correspondence to: Francisco.Rodriguez@pvcf.udl.es

18Amaro Forests - Chap 16 1/8/03 11:53 am Page 182

182 F. Rodríguez et al.

Growth models are often a prerequisite for the prediction of stand-level volume

growth, where height of dominant and codominant trees in even-aged stands is

commonly used as a measure of forest productivity (Monserud, 1984). Traditionally,

these models, whether empirical or mechanistic, have been obtained by ﬁtting

observed data to mathematical functions. Indeed, tree growth models usually

employ a set of equations to describe stand development over time.

The concept of a productivity curve, as deﬁned for poplar plantations (Padró,

1982), describes the r

elationship between the age of the stand and its mean diameter

at breast height (DBH). In fact, the productivity index (i.e. DBH at a reference age,

PI) is seldom determined through direct observations but estimated by productivity

curves using the mean DBH and age of trees in the target stand. Such an estimation

assumes that the DBH growth pattern is associated with PI for a given tree species.

However, DBH–age curves for a given PI can differ signiﬁcantly before and after the

reference age due to factors such as climate and site characteristics (Wang and

Huang, 2000).

For poplar plantations, a parallel is observed between productivity curves and

quality curves (i.e. the r

elationship between age of the stand and its dominant

height). This is because thinning is not performed in the area and pruning practices

have little inﬂuence on the diameter growth (Rodríguez et al., 2001). Under these cir-

cumstances, DBH is a good indicator of yield. The application of productivity

curves to any given poplar plantation allows for an assignment of a productivity

class to the stand and, knowing its mean DBH to any age, it also describes stand

development with time and allows a choice of rotation period based on the stand PI.

The objectives of this study were: (i) to develop a stand-level DBH growth

model speciﬁc for each clone (I-214, Luisa

Avanzo and MC) applicable throughout

the Cinca valley, and (ii) to classify the existing stands in the region by productivity

index.

Materials and Methods

Site description

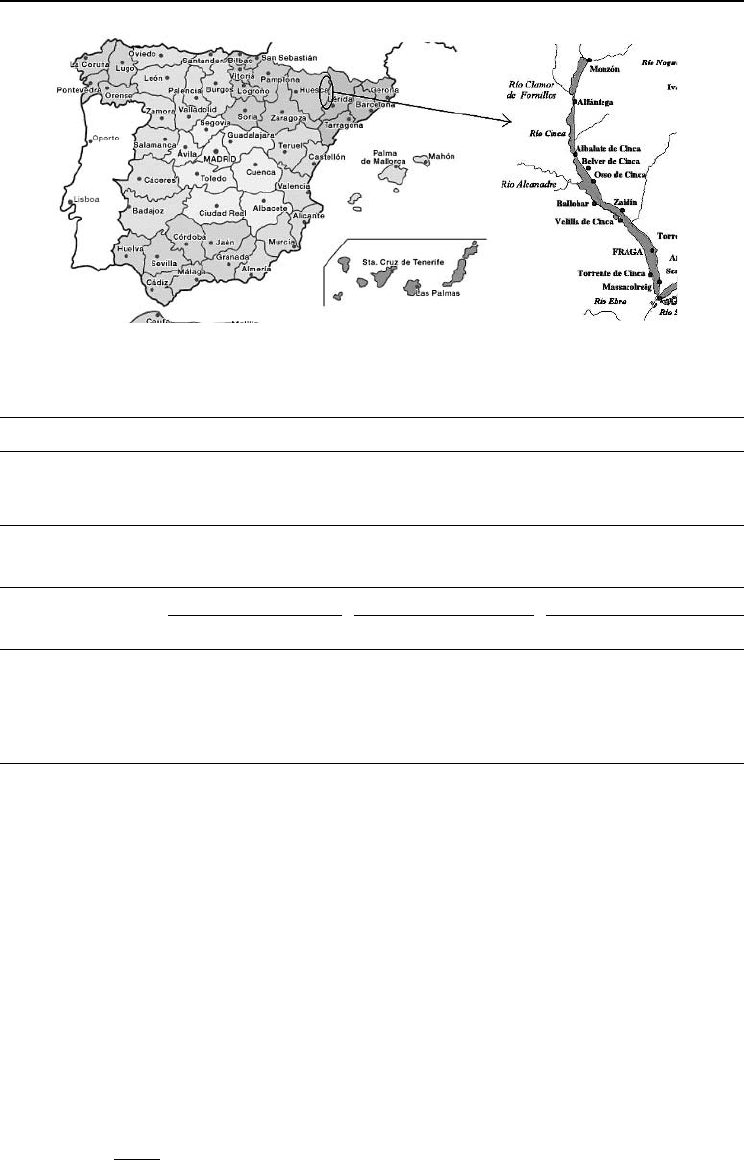
The area of study is located in the Cinca valley (Huesca, Spain), with coordinates 0°

11 to 0° 08

, 41° 55 to 41° 31N (Fig. 16.1), with an average altitude of 188 m above

sea level. Poplar plantations are located in alluvial soils formed principally by grav-

els. The groundwater table is about 2 m deep.

The forest management is characterized by the following steps: (i) 1-year-old

poplars ar

e established on ﬂood irrigation lands following square planting (6 × 6m,

with a total of 278 trees/ha); (ii) tillage is performed yearly to eliminate competition

by weeds; and (iii) the time period between irrigations is 15 days during summer at

a rate of approximately 2000 m

/ha (approximately 15,000 m

/hayear) (Padró,

1992).

The available data were collected throughout the inventoried areas of the Cinca

valley to pr

ovide representative information for a variety of site conditions. For each

felled tree, the following variables were measured: diameter at breast height (DBH),

total height and stand age (all the inventoried areas have the same density; 278

trees/ha). Data originated from re-measured permanent plots (544 DBH × age com-

binations) and temporary plots (295 DBH × age combinations). Table 16.1 classiﬁes

the number of plots by type (permanent or temporary) for each clone, and Table 16.2

summarizes the data collected at the plot level. The number of measured trees by

plot was four in the temporary plots and nine in the permanent plots. I-214, the least

18Amaro Forests - Chap 16 1/8/03 11:53 am Page 183

183 Modelling Diameter at Breast Height Growth

Fig. 16.1. Area of the study.

Table 16.1. Summary of number of plots by type for each clone.

I-214 MC LA Count

Temporary 38 20.9% 141 40.5% 116 37.5% 295 35.16%

Permanent 144 79.1% 207 59.5% 193 62.5% 544 64.84%

Count 182 348 309 839

Table 16.2. Summary of data collected at the plot level

I-214 MC LA

Age (years) DBH (cm) Age (years) DBH (cm) Age (years) DBH (cm)

Count 182 347 309

Average 5.357 14.748 6.541 18.043 5.543 15.914

SD 4.094 12.415 3.919 10.715 2.804 9.0735

Minimum 1.0 2.3 1.0 2.425 1.0 1.075

Maximum 16.0 47.5 16.0 42.35 12.0 39.15

abundant clone in the area, was present in only 182 plots (i.e. about half of the plots

in which the other clones were represented).

Model ﬁtting

The model proposed by Richards (1959) has been widely used in forestry. Its success

can be explained by the inclusion, in its dif

ferent forms, of the basic components of

growth (Equation 1) (Bravo, 1988). Biologically based models, such as the one by

Richards, have the advantage that the extrapolation of results out of the range of the

original data is safer than that for empirical models (Vanclay, 1994). Different forms

of Richards’ model are derived for use in growth modelling; Equation 2 is an inte-

gral form, whereas Equations 2a, 2b and 2c are different forms of the model.

α β

DBH

=⋅DBH

−⋅ DBH

(1)

18Amaro Forests - Chap 16 1/8/03 11:53 am Page 184

184 F. Rodríguez et al.

DBH =⋅ − exp

(

−b t

)

(2)

(

1 ⋅

DBH =⋅ ⋅− exp

(

−b t

)

K PI

(

1 ⋅

DBH =

(

1 ⋅

)

⋅

(

1 − exp

(

−bt

)

⋅−exp

(

−bt

)



1 − exp

(

)



⋅

DBH = PI



⋅1 − exp

(

)





)



where a is the asymptote of DBH (cm), b is a growth rate-related parameter, t is the

age of the stand (years), t

is the reference age (years), c is a shape parameter, K is a

constant and PI is the productivity index (cm).

The procedure for ﬁtting the productivity curve consists of the following steps:

(i) determination of reference age; (ii) parameter estimation of the reference curve; and

(iii) graphic representation of the different curves by PI.

Requisites for selecting an appropriate reference age are: (i) to be high enough

to obtain a r

eliable expression of the quality, and (ii) to not be so high that a large

number of plots cannot be found (Bengoa, 1999). The reference age is usually taken

as the maximum of the average growth curve along the rotation period or, more

straightforwardly, half of the rotation period (Pita, 1964). In poplar plantations for

the region it ﬂuctuates between 6 and 8 years and, for this work, we have chosen a

reference age of 7 years.

In addition to ﬁtting the productivity curves, we also ﬁtted an empirical

height–DBH r

elationship, based on a multiplicative model adapted by Cunia (1979).

Its mathematical formulation is the following:

TH =⋅a DBH

(3)

where a and b ar

e parameters to estimate, DBH is the diameter at breast height (cm)

and TH is the total height (m). A summary of the characteristics of the data set for

ﬁtting the height–DBH model is presented in Table 16.3.

Models 2 and 3 were estimated using the SAS software (1990). For model 2

(non-linear model), the non-linear r

egression (NLIN) procedure with the derivate-

free iterative Marquardt method was applied, and multiple starting values for para-

meters were provided to ensure a least squares solution. Model 3 was ﬁtted using a

simple least square regression technique (the REG procedure).

The coefﬁcient of determination (R

) and the mean squared error (MSE) were

calculated as:

∑

(

−

)

=−

∑

(

Y − Y

)

(4)

∑

(

−

)

MSE =

(5)

−nm

ˆ ¯

where Y

, Y

, Y, m and n are actual Y, predicted Y, observed average Y, number of

parameters, and number of observations, respectively.

18Amaro Forests - Chap 16 1/8/03 11:53 am Page 185

185 Modelling Diameter at Breast Height Growth

Table 16.3. Summary of the data set for ﬁtting a height–DBH model (age in years, DBH and

TH in cm)

I-214 MC LA

Age DBH TH Age DBH TH Age DBH TH

(years) (cm) (m) (years) (cm) (m) (years) (cm) (m)

Count 809 809 809 1816 1816 1816 1415 1415 1415

Average 7.04 20.42 17.87 7.61 20.85 19.50 6.27 18.16 16.99

Variance 23.6 233.8 135.2 16.5 124.8 90.58 7.72 82.35 56.50

SD 4.86 15.29 11.63 4.06 11.17 9.517 2.77 9.075 7.516

Minimum 1.0 2.0 3.17 1.0 2.0 3.76 1.0 1.5 2.9

Maximum 16.0 66.84 44.6 16.0 48.8 40.2 12.0 42.3 36.8

Results

Model 2 was ﬁtted separately for each clone. All parameters were statistically signif-

icant (P < 0.05). A family of anamorphic curves was constructed by changing PI val-

ues. A summary of the ﬁt and the estimated parameters is given in Table 16.4.

A PI was calculated for each of the inventoried plots. We obtained a frequency

distribution of the dif

ferent productivities for each of the three clones studied. From

these distributions it was observed that most of the plots fell within the class of

average productivity, with few plots having very high or very low productivities.

Table 16.5 summarizes the number of plots by PI for each clone.

Model 3 was ﬁtted separately for each clone and, again, all parameters were

statistically signiﬁcant.

All three models exhibited a high R

and a very low MSE.

Table 16.6 summarizes the estimated parameters and the statistics indicating the

goodness of ﬁt.

The graphical analyses of models 2 and 3 are shown in Fig. 16.2.

Table 16.4. Summary of the ﬁt and the estimated parameters.

Clone A b c K R

MSE

I-214 56.0046 0.111167 1.60662 2.6851 0.9242 11.67

Luisa Avanzo 51.7181 0.11277 1.49883 2.4777 0.8612 11.42

MC 46.0016 0.134302 1.60509 2.2143 0.9272 8.34

Table 16.5. Number of plots by productivity index (PI).

PI I-214 MC LA Total

29 33 18.1% 38 10.9% 31 10.0% 102

25 25 13.7% 79 22.7% 58 18.8% 162

21 68 37.4% 148 42.5% 106 34.3% 322

17 47 25.8% 54 15.5% 52 16.8% 153

13 9 4.9% 29 8.3% 62 20.1% 100

Total 182 348 309 839

Table 16.6. Summary of the parameter estimates and ﬁt statistics.

Clone a b R

MSE

I-214 1.65552 0.801669 0.9784 0.013

Luisa Avanzo 1.57215 0.825299 0.9657 0.009

MC 1.71534 0.805359 0.9656 0.011