Amano R.S., Sunden B. (Eds.) Computational Fluid Dynamics and Heat Transfer: Emerging Topics
Подождите немного. Документ загружается.

Sunden ch003.tex 27/8/2010 18: 35 Page 76
76 Computational Fluid Dynamics and Heat Transfer
The matrix
E
can be represented in the form
±
E
according to the positive or
negative value of λ
1
, λ
2
, and λ
3
, that is,
E
= (
+
E
−
−
E
)/2 (42)
Similar expression can be derived for D
F
by replacing the contravariant velocity ˜u
by ˜v and ξ byη inequations(35)–(42). Byadding thematrixformofthedissipative
terms in the governing equation (31), we obtain:
t
∂
+
A
2∂ξ
−
∂
−
A
2∂ξ
+
∂
+
B
2∂η
−
∂
−
B
2∂η
+ I
Q
t
+E
+
ξ
+E
−
ξ
+F
+
η
+F
−
η
= R
ξ
+S
η
(43)
where I represents the unit matrix, and
+
A
,
−
A
,
+
B
, and
−
B
denote the matrices
corresponding to the eigenvalues of the convection flux matrices.
By using the second-order time-difference algorithm, we have
Q
n+1
− Q
n
t
=
1
2
∂Q
∂t
n+1
+
∂Q
∂t
n
(44)
t
∂
+
A
2∂ξ
−
∂
−
A
2∂ξ
+
∂
+
B
2∂η
−
∂
−
B
2∂η
+ I
Q
n+1
− Q
n
t
=−
∂E
+
∂ξ
+
∂E
−
∂ξ
+
∂F
+
∂η
+
∂F
−
∂η
n+1
+
∂R
∂ξ
+
∂S
∂η
n
(45)
Recalling that
∂E
∂ξ
n+1
=
∂E
∂ξ
n
+
∂
A
n
Q
n+1
− Q
n
∂ξ
(46)
∂F
∂η
n+1
=
∂F
∂η
n
+
∂
B
n
Q
n+1
− Q
n
∂η
(47)
Considering the stability, the forward and backward scheme were adopted in the
difference of flux splitting.We can define that:
Q
n+1
i,j
=−t
∇
ξ
E
+
ξ
+
ξ
E
−
ξ
+
∇
η
F
+
η
+
∇
η
F
+
η
n
+ t
c
R
ξ
+
c
S
η
n
(48)
δQ
n+1
i,j
= Q
n+1
i,j
− Q
n
i,j
(49)
where the backward operator, for example in ξ for the E term, can be written
as ∇
ξ
E =0.5 (3E
ξ
−4E
ξ−1
+E
ξ−2
), whereas the forward operator
ξ
E =−0.5
(3E
ξ
−4E
ξ+1
+E
ξ+2
) and
ξ
=0.5 (R
ξ+1
−R
ξ−1
).

Sunden ch003.tex 27/8/2010 18: 35 Page 77
CFD for industrial turbomachinery designs 77
By substituting equations (46) and (47) into equation (45) and considering the
definitioninequations(48)and(49),wecanobtainthefollowingdifferencescheme:
d
W
δQ
n+1
i−1,j
+ d
S
δQ
n+1
i,j−1
+ d
P
δQ
n+1
i,j
+ d
N
δQ
n+1
i,j+1
+ d
E
δQ
n+1
i+1,j
= Q
n+1
i,j
(50)
where
d
W
=−
t
2ξ
(
+
A
)
n
i−1,j
−
t
2ξ
A
+
i−1,j
n
d
S
=−
t
2η
(
+
B
)
n
i,j−1
−
t
2η
B
+
i,j−1
n
d
P
= 1 +
t
2ξ
(
+
A
)
n
i,j
−
t
2ξ
(
−
A
)
n
i,j
+
t
2η
(
+
B
)
n
i,j
−
t
2η
(
−
B
)
n
i,j
+
t
2ξ
A
+
i,j
n
−
t
2ξ
A
−
i,j
n
+
t
2η
B
+
i,j
n
−
t
2η
B
+
i,j
n
d
N
=
t
2η
(
−
B
)
n
i,j+1
+
t
2η
B
−
i,j+1
n
d
E
=
t
2ξ
(
−
B
)
n
i+1,j
+
t
4ξ
A
−
i+1,j
n
Intheaboveexpressions,d
W
,d
S
,d
P
,andd
E
arescalars,whichcanbecalculated
directlyfromfluxvectors. Itis shownthat thepresent schememainlyincludesboth
implicit and explicit parts. Equation (50) isthe implicit part of thepresent scheme,
which can improve the numerical stability when a large time step is used in the
calculation. Because of the application of flux vectors, the computational efforts
can be greatly reduced as compared to other coefficient matrix implicit schemes
for any time step [2]. Equation (48) is the explicit part of the scheme. We found
that the implicit part, equation (50), can be solved by using a two-sweep method,
which is similar to the hopscotch-sweep method but along i (i.e., ξ) and j (i.e., η)
directions. Equation (50) can then be written in the form of the two-sweep form as
follows:
d
S
δQ
n+1
i,j−1
+ d
P
δQ
n+1
i,j
+ d
N
δQ
n+1
i,j+1
= Q
n+1
i,j
− d
W
δQ
n+1
i−1,j
− d
E
δQ
n
i+1,j
(51)
Calculation starts from i =1toi
max
along the i-direction. At each station i of
the time step n+1, the variables δQ
i,j−1
, δQ
i,j
, and δQ
i,j+1
can be obtained along
the j-direction. It is clearly shown that the present scheme consists of an explicit
part of Q
i,j
at any time step “n” and an implicit δQ
i,j
at time step “n+1.”
3.6 StabilityAnalysis
Stability is one of the important aspects in developing a numerical scheme, and
only a stable scheme can be used to simulate the differential equations. In this
Sunden ch003.tex 27/8/2010 18: 35 Page 78
78 Computational Fluid Dynamics and Heat Transfer
section, the stability analysis of the present numerical scheme is addressed. One
of the most common methods of stability analysis is the von Neumann stability
analysis. With this method, a finite Fourier series expansion of the solution to a
modelequationis made,andthe decayor amplification ofeach modelis separately
considered to determine whether the method is stable or not. Analysis showed
that the typical stability limitationforthe explicit scheme equation (49) is the CFL
number restriction. Following the von Neumann analysis, it was shown that the
present implicit scheme is unconditionally stable.
Nonetheless, the determination of stability condition for the present hybrid
scheme is quitedifficult due tothecomplication of the equation systems employed
for the computation. To simplify the analysis, let all η derivatives in equation (47)
equal to zero and all the eigenvalues be greater than zero so that in ξ-direction we
have |A
−
|=0 and |A
−
|=|P
+
E
P
−1
|. In the stability analysis, only one of the two
velocity components was performed. The stability analysis of the other variables
is the same. The experience shows that, if each variable in the equation system is
stable, the entire equation system in general is stable. Suppose that ρ
A
and ρ
M
are,
respectively, the spectral radii of the matrices A and M, where
M =
∂R
∂
∂Q
∂ξ
(52)
The numerical scheme of equations (48) and (49) can be written in the following
scalar forms:
u
n+1
i
=−t
ξ
∇
ξ
E
+
ξ
n
+ t
ξ
c
R
ξ
n
(53)
−
t
ξ
ρ
A
ξ
(u
n+1
i−1
− u
n
i−1
) +
1 +
t
ξ
ρ
A
ξ
(u
n+1
i
− u
n
i
) = u
n+1
i
(54)
Upon substitution ofthe Fourier component ofthe solution into equations (53)and
(54), we have:
u
n+1
i+1
= V
n+1
e
(i+1)θ
√
−1
(55)
The following amplification factor for equations (53) and (54) can be obtained:
|
G
|
2
=
!
ξ +
t
ξ
ξ
ρ
M
[
−2 +2cos(mξ)
]
"
2
+
t
ξ
ρ
A
sin(mξ)
2
ξ + t
ξ
ρ
A
− t
ξ
ρ
A
cos(mξ)
2
+
t
ξ
ρ
A
sin(mξ)
2
(56)
The stability condition of the scheme is that the absolute value of G is less than or
equal to unity for all wave numbers m. From equation (56), the following stability
condition can be obtained:
t
ξ
≤
ξ
ρ
A
+
2ρ
M
ξ
(57)
Sunden ch003.tex 27/8/2010 18: 35 Page 79
CFD for industrial turbomachinery designs 79
From a similar analysis, letting all ξ derivatives in equation (50) equal to zero and
letting all the eigenvalues be greater than zero, we can obtain:
t
η
≤
η
ρ
B
+
2ρ
N
η
(58)
where ρ
B
and ρ
N
represent the spectral radii of the matrices B and N, respectively,
and N is defined as:
N =
∂S
∂
∂Q
∂η
(59)
It is clearly shown that the stability constraint of equations (57) and (58) is due to
the explicit part. Therefore, we can conclude that the present implicit scheme is
unconditionally stable.
By solving the spectral radii of the flux Jacobian matrices for the convective
terms and diffusion terms, we can obtain the following stability conditions:
t
ξ
≤
ξ
|
˜u
|
+ a
ξ
2
x
+ η
2
y
+
2ω
ξρ
ξ
2
x
+ η
2
y
(60)
t
η
≤
η
|
˜v
|
+ a
ξ
2
x
+ η
2
y
+
2ω
ηρ
ξ
2
x
+ η
2
y
(61)
where
ω = max(µ,λ + 2µ,µγ/Pr)
The stability analysis shows that the stability restraint arises from the explicit part
for the present scheme. The implicit part of the scheme is unconditionally stable.
However, from the calculation point of view, the explicit part must be treated
within a certain time step. When the time step increases, the implicit scheme is
activated. From this point of view, the present overall scheme can be judged to be
unconditionally stable. From the practical point of view, however, many factors
such as smoothing of the implicit calculation, local linearization of the nonlinear
equations, and complex geometry, all will constrict the time step. Therefore, the
time step must be selected according to the CFL number as:
t = min(t
ξ
,t
η
) (62)
where
t
ξ
≤
CFL ·ξ
|
˜u
|
+ a
ξ
2
x
+ η
2
y
+
2ω
ξρ
ξ
2
x
+ η
2
y
(63)

Sunden ch003.tex 27/8/2010 18: 35 Page 80
80 Computational Fluid Dynamics and Heat Transfer
t
η
≤
CFL ·η
|
˜v
|
+ a
ξ
2
x
+ η
2
y
+
2ω
ηρ
ξ
2
x
+ η
2
y
(64)
From equations (63) and (64), it is easily found that when CFL≤1, the time step
constriction isthe restriction ofthe typicalexplicit scheme. Forthe present scheme
the CFL number can bechosento be around 15.Anyhow it isclearthat the present
scheme is more economical than a pure explicit scheme.
3.7 Applications in Turbine Cascade
In a practical use of the code, the convergence criterion is one of the important
factorsoftheCFDprogram.Thereareseveraldifferentkindsofconvergencecriteria
tochecktheconvergentstateofthenumericalsolutions.Inthiswork,twoconvergent
criteriaareusedtochecktheconvergenceofthecalculation.OneistheRMSresidue
of the four independent variables and the other is the mass flux error. They are
defined as follows:
Error(RMS) =
100 ×
#
(
u
)
2
+
(
v
)
2
+
(
ρ
)
2
+
(
e
)
2
t
(65)
Error(m
) = 100 ×
m
0
− m
EXIT
/m
EXIT
(66)
The actual computational case studies are given in the following subsections.
3.7.1 C3X turbine cascade
The presentnumerical scheme was tested fora two-dimensional compressibleflow
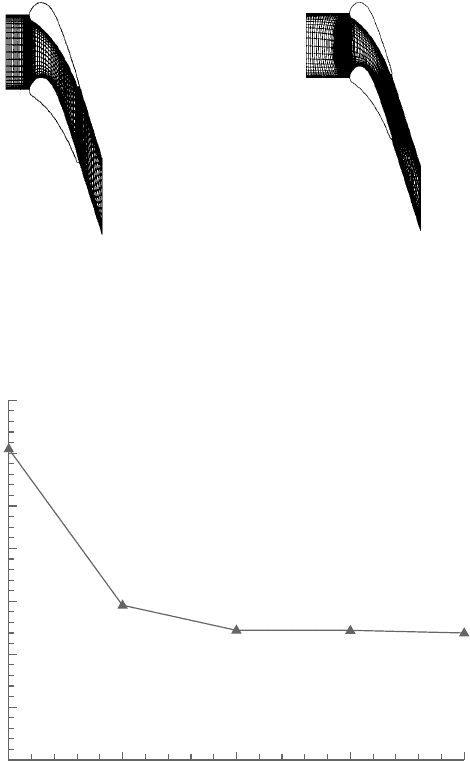
over a C3X turbine cascade [2,34] by using the algebraic H-mesh as shown in
Figure 3.2. The flow considered corresponds to the case 144 of the experiment
conducted by Hylton et al. [34]. The geometric inlet and exit angles of the blade
are 0 degrees and 72degrees, respectively.The flow conditions attheinlet are total
pressure P
To
=7.899kPa, total temperature T
To
=815K, and the inlet Reynolds
number based on the true chord Re=0.63×10
6
. The ratio of exit static to inlet
total pressure is 0.59. The flow was assumed to be fully turbulent in the entire
computation domain.
Theeffectsofthemeshrefinementstudyforcase144wereconductedpriortothe
computations.Thedifferentlevelsofthemeshesbasedonthebasicsize43×12are
showninFigure3.3.Thestudyshowedthatthemassfluxresidualtendstoapproach
a certain level with the increase in the mesh size. It was suggested that the mesh
size of 86×24 is sufficient for a grid-independent condition. In order to assess the
impact of the present scheme, the study of the influence of the CFL number was
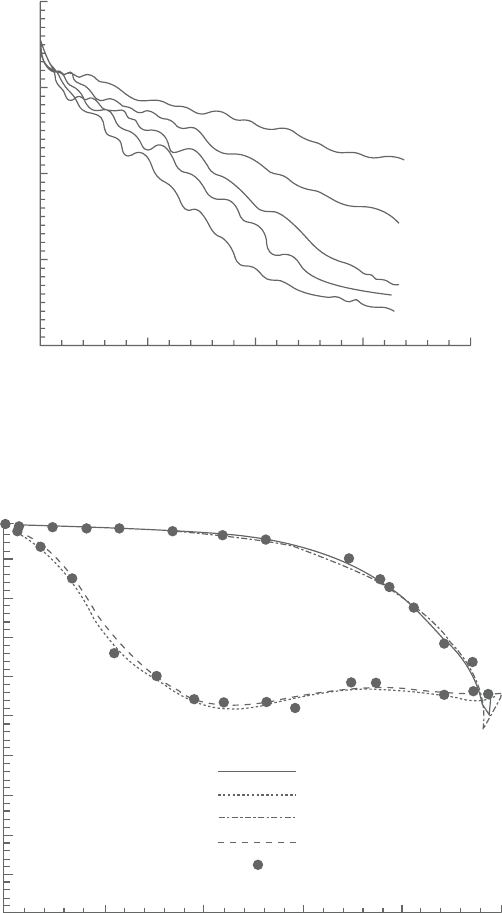
investigated. Figure 3.4 shows the typical convergent histories with different CFL
numbers (1, 5, 7, 9, and 11) by using a mesh distribution of 86×24. The research
shows that when the CFL number increases, the convergent rate is improved. The
results also show that when the CFL number is greater than 7, the improvement
in the convergent rate is small. If the CFL=1, the computational performance is
Sunden ch003.tex 27/8/2010 18: 35 Page 81
CFD for industrial turbomachinery designs 81
(b) Body-fitted H-mesh(a) Algebraic H-mesh
Figure 3.2. Computational meshes.
2.01.5
Magnification factor for mesh size
1.0
0.0
0.1
0.2
0.3
0.4
|(m
in
m
out
)/m
out
|%
0.5
0.6
0.7
2.5 3.0
Figure 3.3. Mesh refine study.
similar tothe case ofexplicit scheme. Inthepresent computation, the CFLnumber
is selected in the range between 5 to 11. It is clear that the present scheme is more
effectivethan the explicitscheme. It is well known that refinementof the high-grid
aspect ratio influences the convergence of the calculation.
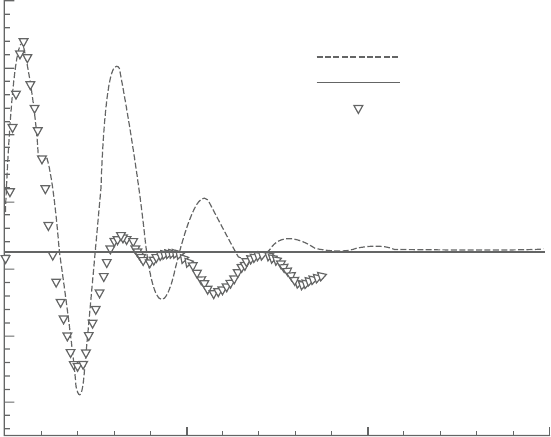
Figure 3.5 shows good agreement of the present predictions for surface static
pressuredistribution withthe experimentaldata measuredbyHylton etal. [34]and
N–S computations by Kwon [35]. Figure 3.6 presents the computed Mach number
Sunden ch003.tex 27/8/2010 18: 35 Page 82
82 Computational Fluid Dynamics and Heat Transfer
Time step
Error (%)
0
10
−4
10
−3
10
−2
10
−0
10
−1
200 400 600 800
CFL = 1
CFL = 5
CFL = 7
CFL = 8
CFL = 11
Figure 3.4. Computational convergent histories.
1.0
1.0
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0.0
0.80.60.40.20.0
x/c
Present (pressure side)
Present (suction side)
Kwon (pressure side)
Kwon ((suction side)
Experiment
p/p
11
Figure 3.5. Blade surface static pressure distributions.

Sunden ch003.tex 27/8/2010 18: 35 Page 83
CFD for industrial turbomachinery designs 83
0.12
0.23
0.41
0.87
0.87
0.87
Figure 3.6. Contour of computed Mach.
contours. The results show that the flow is entirely subsonic and the computed
maximum Mach number is about 0.87. The wakes associated with the airfoils are
clearly seen in the figure. It is also shown that the stagnation point occurs near the
nose of the blade surface. These features are consistent with those expected in a
cascade flow.
Next, the heat transfer coefficient was computed and compared with the
experimental data. It can be seen in Figure 3.7 that the computed heat transfer
coefficientis ingood agreement with theexperimental dataon thepressure surface
except near the leading edge. However, the computed heat transfer coefficient was
overpredicated in the downstream region immediate vicinity of the leading edge
alongthesuctionsurface.Thisdiscrepancymaybecausedbytheheattransfereval-
uation through the energy equation that is coupled with the momentum equations.
In the experiments, the flow field starts from laminar at the upper stream and then
undergoes transition to become fully turbulent. However, in the calculation, the
flow was assumed to be fully turbulent resulting in the overprediction of the heat
transfer coefficient near the leading edge of the suction surface.
Figure 3.8 shows the convergent history when using these two types of
H-meshes. There are slight differences appearing between the two mesh mod-
els. It seems that the algebraic H-mesh has a better convergent property than the
body-fitted H-mesh.

Sunden ch003.tex 27/8/2010 18: 35 Page 84
84 Computational Fluid Dynamics and Heat Transfer
1.0
0.9
0.8
0.7
0.6
0.5
H/H
0.4
0.3
0.2
0.1
0.0
0.0 0.2 0.4 0.6
Present (pressure side)
Experiment (suction side)
Experiment (pressure side)
Present (suction side)
x/c
0.8 1.0
Figure 3.7. Heat transfer coefficient distribution on blade surface.
Time step
Error (%)
0
10
−4
10
−3
10
−2
10
−0
H-mesh
Body fitted mesh
10
−1
200 400 600 800
Figure 3.8. Mesh influence of the convergent histories.
Sunden ch003.tex 27/8/2010 18: 35 Page 85
CFD for industrial turbomachinery designs 85
−72
−74
−76
−70
−80
−82
−84
5000 1000 1500
Time step
Outflow angle
Present
Experiment
Denton
Figure 3.9. Convergent histories of the outflow angle.
3.7.2 VKI turbine cascade
AnothertestcaseofthepresentalgorithmistheflowaroundtheVKIturbinecascade.
In the calculation a 77×21 H-type mesh, which is similar to that shown in Figure
3.2a, was used with the same surface definition as suggested by Xu andAmano as
well as Kwon [2,35]. For comparison with other computational results, the mesh
points were also selected to be the same as those suggested by Sieverding [38].
The flow conditions were the same as in his experiments. Figure 3.9 shows the
convergence history forthe average outflow angle.Thepresent computations show
the angle effectively reaching a steady value, which is in good agreement with the
experiment [37]. Further noted in the figure is the convergent rate of the present
scheme being slightlybetter than that in the method proposed by Denton [37].The
computed outflow angle with different isentropic exit Mach numbers is shown in
Figure 3.10. The isentropic Mach numbers were calculated using the Bernoulli’s
equation with total pressure at the entrance and static pressure on the wall. The
results show that the present calculation agrees well with the experiment. The
calculatedexitanglewhentheexitisentropicMachnumberis1.2isalmostthesame
as that of Denton. Figure 3.11 shows the computed blade surface isentropic Mach
number distributions compared with both the experiment and computed results by
Denton [37]. It shows that the present computation agrees with the experimental
