Amano R.S., Sunden B. (Eds.) Computational Fluid Dynamics and Heat Transfer: Emerging Topics
Подождите немного. Документ загружается.

Sunden ch003.tex 27/8/2010 18: 35 Page 86
86 Computational Fluid Dynamics and Heat Transfer
0.6
0.7 0.8 0.9 0.1 1.1 1.2
−79.0
−79.5
−80.0
−80.5
−81.0
Denton
Experiment
Persent
M
IEXIT
Outflow angle
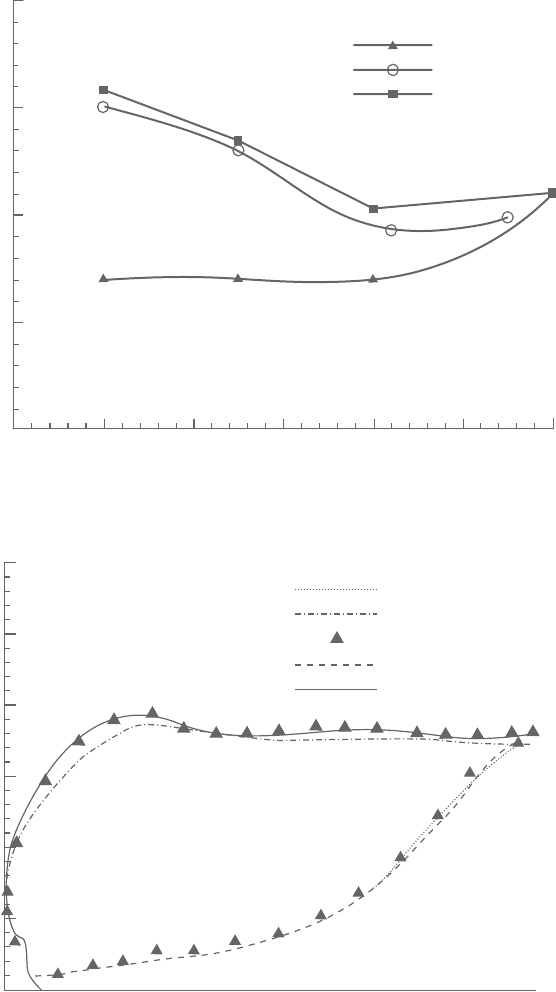
Figure 3.10. Outflow angle with Mach number.
Pressure (Denton)
Suction (Denton)
Present (pressure side)
Present (suction side)
Experiment
x/c
3.0
0.0
0.2
0.4
0.6
0.8
M
10
1.0
1.2
3.2 3.4 3.6 3.8 4.0
Figure 3.11. Isentropic Mach number distributions on the blade surface.
Sunden ch003.tex 27/8/2010 18: 35 Page 87
CFD for industrial turbomachinery designs 87
10
10
0 4
0 7
0 8
Figure 3.12. Contour of computed Mach number.
ones when compared with those by Denton. Figure 3.12 is Mach number contour
between the cascade blades.
An efficient numericalscheme for computationsof the flow andheat transfer in
turbine cascadeflowwasproposedand tested. It was demonstrated thatflux-vector
scheme has the following advantages:
•
The flux-vector scheme avoids the coefficient matrix operation and omits any
iteration within the same time-step calculation. Therefore, less computational
effort is needed in the calculation.
•
The present algorithm possesses thepositivefeaturesof the explicit and implicit
algorithms.Becausethepresentalgorithmdidnotuseapproximationfactor(AF)
inthe time-marchingprocess, the CFLnumber canbe chosento belargeenough
to save computational time. Furthermore, since the present scheme includes an
implicit part, the method improves the convergence ability especially for the
large time-step computations.
•
The computation shows that the present scheme has a similar convergent rate
compared with the multigrid method developed by Denton [37]. The upwind
scheme isused in theFVS schemeinorder toimprove thestability of theoverall
scheme.
•
The flux-vector method hasseveralmerits such as goodconvergenceandoverall
accuracyinpredictingtheflowfieldandheattransferaroundtheturbinecascades.
This fact was supported by the validation test shown in good agreement with
experiments.

Sunden ch003.tex 27/8/2010 18: 35 Page 88
88 Computational Fluid Dynamics and Heat Transfer
In the present method, the dissipation terms were incorporated into the time-
derivativeterms.Thischaracter rendersthe schememoreaccurateaswellasavoids
the eigenvalue stiffness when the calculation is performed in a low Mach number
rangeandacceleratestheconvergenceofthesimulation.Finally, itisshownthatthe
present scheme is more advantageous than common implicit and explicitschemes.
The present scheme can be easily extended to full three-dimensional turbine flow
calculations.
3.8 Numerical Method forThree-Dimensional Flows
The Navier–Stokes equations can bewritten in a body-fittedcurvilinear coordinate
system (ξ, η, ζ) as follows:
∂(J
−1
U)
∂t
+
∂F
∂ξ
+
∂G
∂η
+
∂H
∂ζ
=
∂F
V
∂ξ
+
∂G
V
∂η
+
∂H
V
∂ζ
(67)
where the convective terms can be written as:
∂F
∂ξ
= A
∂U
∂ξ
(68)
∂G
∂η
= B
∂U
∂η
(69)
∂H
∂ζ
= C
∂U
∂ζ
(70)
The detailed expressions in the above equations can be found in Turkel and Vatsa
[15]. Following the previous section, a dissipation model employed in this study is
a nonisotropic model, in which the dissipative terms are given as a function of the
spectral radii of the Jacobian matrices associated with the appropriate coordinate
directions. The dissipative terms in the three directions of the coordinates have
forms similar to that discussed in previous section and in Turkel and Vatsa [15].
This method can overcome the effect of eigenvalue stiffness on the convergence
of an incompressible flow calculation by using the time-matching scheme. The
dissipation terms were incorporated into the time-derivative terms. In this way, the
dissipationtermscanenlargetheeigenvalueofthetime-derivativeterms,whichwill
benefit the flow solver convergence, in particular when the code is used to solve
the low-speed flow problems. The dissipation term that is required to stabilize the
schemeisimplemented ina convenientmanner by modifyingthe convectivefluxes
as follows:
F
ξ+1/2,η,ζ
= 0.5 ∗(F
ξ,η,ζ
+ F
ξ+1,η,ζ
) −d
ξ+1/2,η,ζ
(71)
G
ξ,η+1/2,ζ
= 0.5 ∗(G
ξ,η,ζ
+ G
ξ,η+1,ζ
) −d
ξ,η+1/2,ζ
(72)
H
ξ,η,ζ+1/2
= 0.5 ∗(H
ξ,η,ζ
+ H
ξ,η,ζ+1
) −d
ξ,η,ζ+1/2
(73)

Sunden ch003.tex 27/8/2010 18: 35 Page 89
CFD for industrial turbomachinery designs 89
Thetermsd
ξ+1/2,η,ζ
,d
ξ,η +1/2,ζ
,andd
ξ,η,ζ+1/2
representthedissipativetermsinξ−,
η−, and ζ− directions, respectively, which can be found in Xu and Amano [1,3].
Usingequations (2)–(4), thetimederivativeofdissipativeter ms canbe writteninto
a matrix form as:
D = [1,d
ξ+1/2,η,ζ
,/u, d
ξ,η+1/2,ζ
/v, d
ξ,η,ζ+1/2
/w,1]
T
(74)
By substituting the dissipative terms of equation (74) into equations (71) through
(73) and incorporating into equation (67), we obtain:
I +
D
U
∂(J
−1
U)
∂t
+
∂F
∂ξ
+
∂G
∂η
+
∂H
∂ζ
=
∂F
V
∂ξ
+
∂G
V
∂η
+
∂H
V
∂ζ
(75)
Thesecond-ordernumericaldissipationtermsweresetsothatthevariablesdecrease
exponentially as a function of time. This technique allows a computation to damp
out high-frequency errors at the initial stage of iterations and, therefore, avoids
the second-order numerical dissipation terms to dissipate when the computation
approaches a converged state.A finite-volume algorithm based on a Runge–Kutta
time-stepping scheme [15] is used to obtain the steady-state solutions by solving
theNavier–Stokesequations.TheturbulencemodelusedinthisstudyisaBaldwin–
Lomax turbulence model [32]. The meshes generated in this study are hexagonal
meshes; the grid lines near the solid wall are almost normal or parallel to the solid
walls. In order to simplify the programming effort, the turbulence equations were
applied along grid lines rather than in the direction normal to the solid boundaries.
This avoids flow calculations in all the normal directions to the solid wall and
the necessary interpolations of the flow variables. During the calculations, it is
difficulttokeep allthe y
+
valueswithinasmalllevel,especiallyclose tothecorner
region.Therefore,the wall functionwas usedin thecalculation.The staticpressure
coefficient is defined as:
C
ps
=
P − P
01
p
01
−p
s2
(76)
The total pressure loss is defined as:
C
p0
=
P
01
− P
0
p
01
−p
s2
(77)
where
p
s2
represents the mass average static pressure of the blade exit plane.
3.9 Applications of Three-Dimensional Method
3.9.1 Analysis of pitch-width effects on the secondary
flows of turbine blades
The inlet and outlet boundary conditions used in the computations were taken
from measurement.The total pressure at inlet was equal to the test [38] for all the
Sunden ch003.tex 27/8/2010 18: 35 Page 90
90 Computational Fluid Dynamics and Heat Transfer
calculations. At the exit plane, one of the most critical conditions was to specify
thestatic pressure.Theaverage exit pressurein theexperiment[38] was usedin the
calculations. The asymptotic boundary conditions with second-order streamwise
derivatives ofvariables were set tozero.The overallmass conservationthrough the
bladeflowpassageisimposedbycor rectingtheoutletvelocitycomponentswiththe
calculatedvelocityprofilesontheplanenexttotheoutletandinletflowmassduring
iterations.The no-slip wall boundary conditions are used for all the solid walls.
Grid-converged solutions for the high-speed viscous flows over a turbine blade
shouldbe obtainedwith sufficientlyfinemeshes. However,a computationwith fine
meshes is very time consuming and difficult to assess the numerical accuracy of
the solution. In fact Inoue and Furukawa [23] reported that it was difficult to opti-
mizetheartificialdissipation coefficientsbyusinga commonmethodthatimpaired
accuracy and reliability of the schemes to predict a cascade performance. To pre-
dict a high Reynolds number turbulent flow, highly clustered grids are required
toward the wall. The grid refinement study was conducted through the computa-
tional uncertainty study. The relationship between the calculated mass residual,
100×|m
in
−m
out
|/m
out
%, and various grid sizes was tested to identify the point
where the mass residual reaches its asymptotic value. In this study, the systematic
grid refinementstudiesareperformed.Thegridrefinementstudywasconductedby
using Richardson extrapolation method [39]. The mass factor, f =|1−m
in
/m
out
|,
is used to evaluate the grid refine study. Using the fine grid calculation with a
magnification factor of 3, we obtain f
1
=0.18×10
−4
. Then we change the grid
with the magnification factor to 2, and obtain f
2
=0.85×10
−4
. In this case, the
error is ε =100×(f
2
−f
1
)/f
1
=0.67%. For a grid increase rate, IN=1.5, the fine
grid value of the grid convergence index (GCI) for the present second order is
GCI=3ε/(IN
2
−1)=1.61%.Although the confidence in the GCI as error band is
not justifiable, it shows the current grid structure to be conservative. It also shows
that the uncertainty in the current calculation for the mass conservation is within
1.61%. The distance of the first mesh from the solid surface was chosen so that a
maximumy
+
valuebecomeslessthan15, whichisconsidered tobefineenoughfor
the presentcalculations.The mesh has 45×41×115 node pointsin the pitchwise,
spanwise, and streamwise directions, respectively, which was identified to an opti-
malsituationasagrid-independentstate.Theblade-to-bladecomputationalmeshis
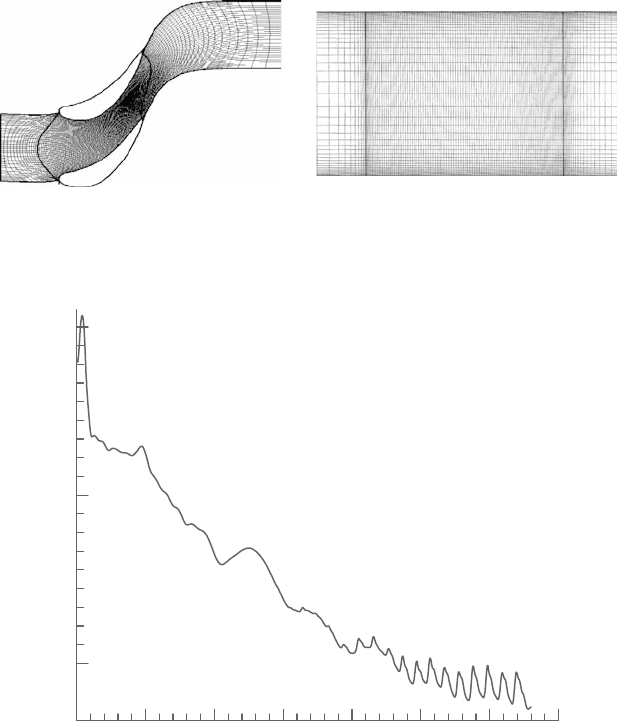
showninFigure3.13.Themeshisfor medconsistingofthreezones:upstreamofthe
blade,inside theblade, anddownstreamof thebladesections.For comparisonwith
thetestresults[38], theoutletofthe calculationplanewasselectedtobeperpendic-
ular to the x-direction (axial direction), which corresponds to the tested exit plane.
Most CFD studies [40–42] on turbomachines were mainly based on a linear
cascade of high-turning turbine blades where the secondary flow was very strong.
Inthisstudy, anannularturbinebladewasfocused, whichissimilartoactualturbine
statorvanes.TheairfoilmodelinvestigatedbySieverding[38],wherethebladetests
were cited from NACATN D-3751, is used for validation of the code.The tip and
rootradiiare0.355and0.283m,respectively.Thestaggerangleis42.5degreeswith
respectto axialdirection andthe bladeaxial widthlength, C
a
=0.087m.Theblade
profileisconstantalongthebladeheightandisuntwisted.Threerootpitch-to-width
Sunden ch003.tex 27/8/2010 18: 35 Page 91
CFD for industrial turbomachinery designs 91
(a) Blade-to-blade mesh at middle span (45 x 117) (b) Meridional mesh (41 x 117)
Figure 3.13. Calculation meshes.
0
10
−1
10
−2
10
0
Mass error
No. of steps
1000 2000 3000 4000 5000 6000 7000
Figure 3.14. Convergence history.
ratios, b/C
a
=0.639, 0.973, and 1.460, are studied here. The root pitch-to-width
ratio, b/C
a
, was varied by altering thenumber ofblades.Threeblade numberswere
used in the calculation: 26, 21, and 14.These calculations were compared with the
experimental data of the annular turbine blades [38].
The computations were assumed to be converged when the mass flow error
became less than 0.1% of the inlet mass flow rate. The mesh used in this study
and typical convergence history are shown in Figure 3.14.The convergence speed
became slowafterthe mass flowerror became closeto 0.1%. In allthe plots shown
in this section, the viewpoint is set to look in the downstream direction from the
Sunden ch003.tex 27/8/2010 18: 35 Page 92
92 Computational Fluid Dynamics and Heat Transfer
0 10203040506070
Beta
−40
−50
−60
−70
−80
−90
Blade Height
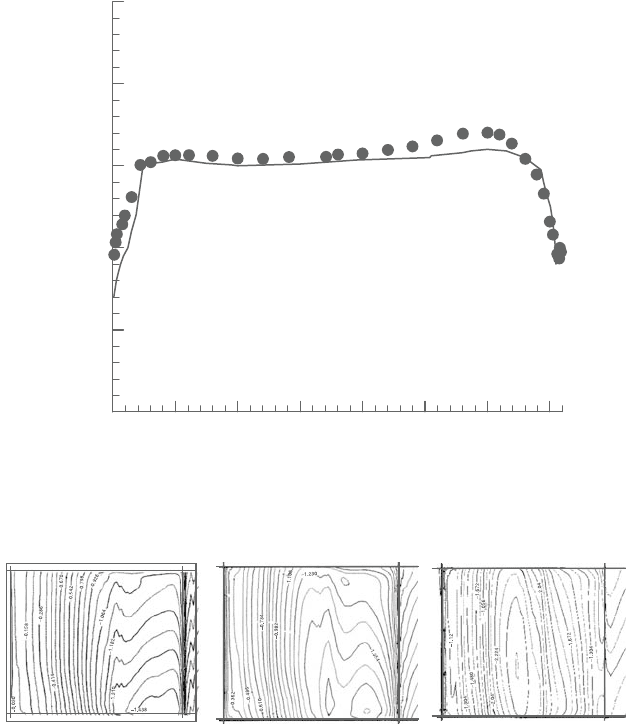
Figure 3.15. Average spanwise flow angle distribution at x/C
a
=0.9 (dot is exper-
imental results).
(a) b/Ca = 0.639 (left is leading
edge and top is casing).
(b) b/Ca = 0.986. (c) b/Ca = 1.460.
Figure 3.16. Static pressure coefficient distributions on the suction surface of the
blade.
upstream location, with the pressure surface on the left-hand side and the suction
surface on the right-hand side.
Figure 3.15 shows the comparison of the experimental results [38] with the
present computations for the average spanwise flow angle distribution located at
x/C
a
=0.9. The computations are in agreement with the experiment. Figure 3.16
shows thestatic pressurecoefficientdistributions nearthe suctionsurf ace ofblades
for different root pitch-to-width rations, b/C
a
. The inception and transport of the
passage vortex and its impact on the surface boundar y layers present different

Sunden ch003.tex 27/8/2010 18: 35 Page 93
CFD for industrial turbomachinery designs 93
b/C
a
= 0.639
b/C
a
= 0.973 b/C
a
= 1.460
Sa1
Sa2
Sa2
Sa1
Figure 3.17. Velocity vectors atthe leadingedge ofthe bladeat0.28%heightfrom
root.
characteristics for different b/C
a
. There is a region near the wall corner where the
chordwise and spanwise pressure gradients are small. It is also clear from Figure
3.16 that the possible boundary layer separation lines occur forcasesb/C
a
=0.639
and 0.986, and they are located at the cor ners of the hub and trailing edge. The
separation region for the case b/C
a
=1.460 is located at 50% of C
a
position. The
separationlocation seemstomoveforwardas b/C
a
increases.Thisfeatureconfirms
that the inception of the passage vortex developed near the airfoil leading edge
and grew fast when the pitch b/C
a
was increased. Figure 3.16 also shows that the
pressure coefficient on the suctionsurfaceislower forlarger b/C
a
.This is because,
as b/C
a
increases, the flow constraintfrom the bladebecomes small, and therefore,
the blade’s local curvature plays an important role. For the case of b/C
a
=0.639
and 0.986, a vortex develops faster near the blade tip and moves toward the casing
because thelocalpitch size at thetip is much larger than that atthe hub. In the case
of b/C
a
=1.460, thecasing and thehub vortex havesimilar characteristics because
b/C
a
is large enough, thus causing the blockage to be small enough so that it does
not restrict the flow. The flow characteristics are dominated by local curvature for
b/C
a
larger than 1.46.
Theexperimental data[43,44] indicatedthat one ofthe mostimportant features
in a turbine blade boundary layer is the occurrence of the separation and saddle
point on the end wall near the leading edge. The predicted boundary layer flow
patterns for different b/C
a
near the hub leading edge at 0.28% height are shown
in Figure 3.17. The calculations show that there is a saddle point for all b/C
a
.
Two attachment lines, Sa1 and Sa2, and two separation lines, Ss1 and Ss2, can be
identifiedfrom thevelocityvectors.The separationlinescorrespond tothetwolegs
of the horseshoe vortices formed near the leading edge. The separation line Ss2
is pushed away from the leading edge. The first separation line Ss1 moves around
the leading edge and moves against the freestream flow direction and it merges
with theflow coming fromthe upstream directionto form a suction-sidehorseshoe
vortex.TheseparationlineSs1isalsodevelopedalongthesuctionsideoftheblade,
which can be seen from the static pressure coefficient distribution in Figure 3.17.

Sunden ch003.tex 27/8/2010 18: 35 Page 94
94 Computational Fluid Dynamics and Heat Transfer
b/C
a
= 0.639 b/C
a
= 0.973
b/C
a
= 1.460
Figure 3.18. Velocity vectors in the meridional surface before the leading edge.
0.7
0.8
PS
0.9 1.0
1.1
1.2
1.3
13
HUB
12
b/C
a
= 0.986 (experiment)
−0.85
−0.8
−1.1
−0.95
−1.15
−0.75
−1.3
−1.25
−1.05
−0.9
−1.05
−1.2
−0.1
b/C
a
= 0.986
−0.85
−0.8
−0.7
−0.75
−0.95
−0.9
−0.1−1.05
−1.35
−1.55
−1.45
−1.4
−1.5
−1.6
−1.15
−1.1
−1.2
−1.15
−1.2
−1.05
−1.1
−1.2
−1.7
−1.35
−0.95
−0.9
−1.25
b/C
a
= 1.460
−0.8
−0.7
−0.6
−0.5
−0.9
−1.0
b/C
a
= 0.639
−1.1
−1.2
Figure 3.19. Static pressure coefficient contour at x/C
a
=0.9.
The locations of the saddle points are closer to the leading edge for larger pitch
sizes. This is why some of the flow visualization [42] did not find a saddle point
if the experiment did not extend sufficiently far upstream. The velocity vectors in
the meridional plane upstream of the leading edge are shown in Figure 3.18. The
vector distributions show that there is a separation region occurring upstream of
theleading edge. Itis shownthat theregion ofthe separationdepends onthe pitch–
width ratio, b/C
a
.Alowerb/C
a
generates arelatively larger separationregion.This
characteristic determines the location of the saddle points on the blade-to-blade
plane depending on the pitch–width ratio b/C
a
. The present computations show
that there is a saddle point upstream of the leading edge attributed to the blockage
of the blades. With increasing blockage, the secondary saddle vortices move more
forward and the separation in the front of the blade becomes smaller.The location
of the saddle point depends on the b/C
a
as well as the local curvature of the blade.
Figures 3.19, 20, and 21 show the contours of the static pressure coefficient
C
ps
distributions at 90%, 100%, and 110% chord positions, respectively, from
the leading edge for different values of b/C
a
. The measurement results for –C
ps
at 90% chord position is plotted for comparison with the calculations. It should
be pointed out that the measurement plane in the experiments [44] is defined to

Sunden ch003.tex 27/8/2010 18: 35 Page 95
CFD for industrial turbomachinery designs 95
−0.80
−0.7
−0.65
−1.0
−1
−1.1
−0.95
−0.85
−0.85
−0.8
−1.15
−1.05
−1.20
−1.05
−1
−1.1
−1.15
−0.85
−0.9
−0.95
65−0.7
−0.75
−1.35 −1.3
0.4
−1.25
−1.05
−0.95
−0.85
−0.8
−0.75
−0.7
−0.65
−0.75
−0.8
−0.95
−0.85
−0.9
−1.1
−1.35
−1.4
−1.3
−1.25
−1.05
−1.15
−1.85
−0.9
−0.7
−0.65
−0.8
−
0.95
−1
−
.
−8
−1.0
−1.2
b/C
a
= 0.639
(contour value from
−1.15 to −0.6 with
increment 0.05)
b/C
a
= 0.973
(contour value from
−1.3 to −0.6 with
increment 0.05)
b/C
a
= 1.460
(contour value from
−1.6 to −0.6 with
increment 0.05)
−0.75 −0.7
−0.65
Figure 3.20. Static pressure coefficient contour at x/C
a
=1.
−1.1
−
1.35
−1.3
−1.25
−1.15
−1.05
−1.9
−0.85
−0.8
−0.95
−0.9
−0.85
−0.8
−0.70
−0.7
−0.75
−1
−1.05
−1.95
−
0.85
−0.9
−0.8
−0.75
−0.65
−0.7
−0.65
−1.1
−1.45
b/C
a
= 0.639
(contour value from −1.1
to −0.65 with increment 0.05)
b/C
a
= 0.973
(contour value from −1.35
to −0.75 with increment 0.05)
b/C
a
= 1.460
(contour value from −1.35
to −0.8 with increment 0.05)
−1.3
−1.25
−1.2
−1.05
−1.45
−1.1
−1.5
−1.95
−0.9
−0.85
−0.8
−0.95
−0.95
0.9
−1
−0.85
−0.8
0.5
−1.35
Figure 3.21. Static pressure coefficient contour at x/C
a
= 1.1.
be perpendicular to the axial direction while the computations are along the mesh
direction, which causes a slight discrepancy. Figure 3.19 shows that the compu-
tation and measurement are in good agreement with each other. The results for
differentb/C
a
show that for smaller b/C
a
, the lowestpressure becomes higher than
those with larger pitch cases. The core of the secondary vortex occurs at different
locations for all three cases. For the smaller b/C
a
, the secondary vortex appears
closer to the corner of the hub on the suction side. For larger b/C
a
, the vortex core
moves awayfrom the suction-side toward thepressure side. When compared tothe
different axial location of C
ps
, it is shown that the vortex core is developed and
moves away from the suction side, to the middle point between the suction and
pressure-side surfaces. As the fluid moves out from the blade passage, the vor-
tices become very small. This is because the blade-to-blade pressure gradient is
reduced. This vortex core is part of the leading edge vortex. Initially, the vortex
occursveryclosetothesuction-sidewallandthenitdevelopstowardtheexitplane.
At the same time, the horseshoe vortex at the pressure-side leg, Ss2, mixes with
the secondary flow and rapidly decays. This phenomenon is in good agreement
with the measurements for the pitch–width influence in the linear cascade [40].
