All?gre Claude J. Isotope Geology
Подождите немного. Документ загружается.


5.3.1 Uncertainties introduced when collecting samples
A question arises before taking samples. Should the sample be taken at random? Such
an approach looks rigorous as it r ules out any subjectivity. Unfortunately, if we set about
th is ‘‘blindly’’ we would ‘‘knowingly’’ introduce systematic uncertainties. For example,
if we sample rocks from a massif of granite, a random sample may include weathered
rocks, rocks in contact w ith neighboring ones of di¡erent origins and ages, and which are
liabletobe contaminated bysu ch contact attectonic faults, etc. In practice, we try to de¢ne
a homogeneous and representative geological whole (various units of the granite m assif)
and then try to take a random sample of that. It is di⁄cult to evaluate the uncertainty of
a sample if on ly one sample is taken. If several are taken, the results must be treated as for
anordinarymeasurement,assumingarandomuncertaintyof1=
ffiffiffiffi
N
p
where N isth e number
of samples collected. Each investigator must think about this sampling question and
solve it (not forgetting any hidden structures) by combining statistics and ...geological
common s ense!
5.3.2 Physical uncertainties on an individual measurement
Unc e rtainties on ages obtaine d f rom parent de cay m et hod s (
14
C,
10
Be,etc.)
Webegin with the dating equation, noting ¼
14
C/C
total
or ¼
10
Be/
9
Be. ¼
0
e
lt
from
which t ¼1/
l
ln(
0
/).
Following the rulesg ivenearlier, th e uncertainties arewritten:
Dt ¼ D
1
l
lnð
0
=Þþ
1
l
Dð
0
=Þ
ð
0
=Þ
Dt ¼
Dl
l
2
lt þ
1
l
D
þ
D
0
0
Dt ¼
Dl
l
t þ
D
l
þ
D
0
l
0
Sampling
Chemical and isotopic
analysis
Age computation
Geological
interpretation
Sampling
uncertainties
Systematic + random
Analytical
uncertainties
Uncertainties with:
Geochronological
model
with total
uncertainty
=
Sum of uncertainties
• Computation
• Histograms
• Correlations
• Chemical contamination
• Physical measurement
++
Figure 5.9 Determining a geological age while allowing for uncertainties affecting each stage.
167 Sources of uncertainty in radiometric dating
Dt ¼
Dl
l
t þ
D
e
lt
þ D
0
1
l
0
:
Wesupposethat l and
0
arenegligible.Thus:
Dt
D
0
le
lt
:
Exercise
We wish to calculate the uncertainty associated with the determination of a
14
C age. We
accept that the uncertainty on the
14
C/C measurement is 2%. We ignore the uncertainty
affecting the estimate of (
14
C/C)
0
(which is far from negligible in practice) and consider that
the uncertainty on the radioactive constant is 1/1000.
Calculate the absolute and relative uncertainties committed for ages of 500, 5000, 10 000,
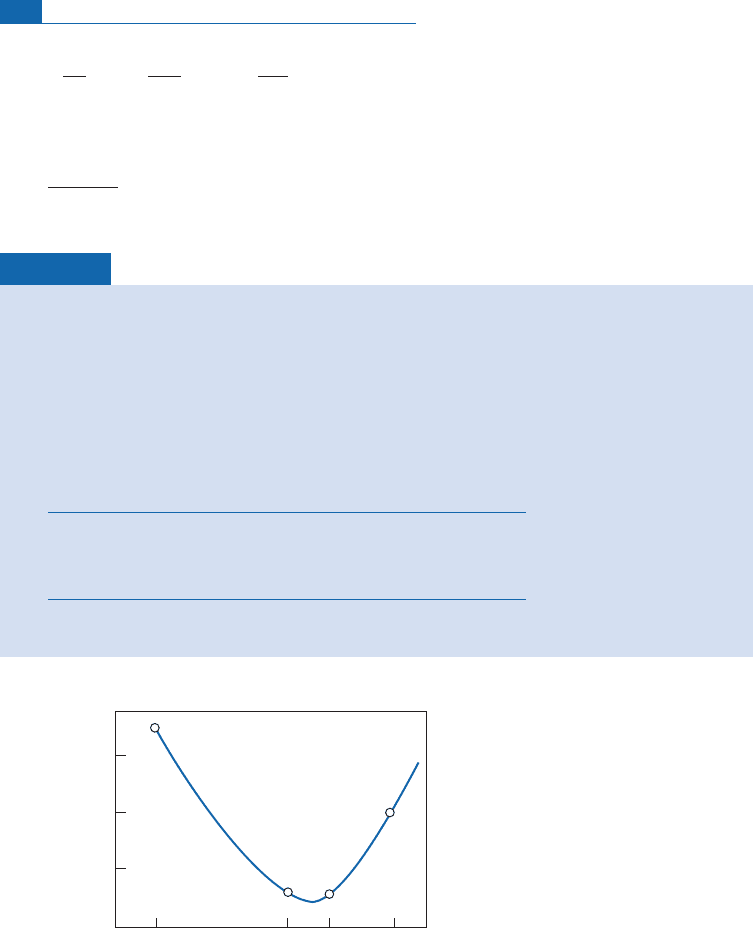
and 30 000 years. Plot the relative uncertainty curve against age.
Answer
We get:
Age (yr) 500 5000 10 000 30 000
t
(yr) 176 302 554 6219
t/t
(%) 35 6 5.5 20
The curve of (
t
/
t
) diverges towards the low and high values of
t
(Figure 5.10).
Overal l e s timation of u nce rtai nt yon l o n g half -lifeparent ^ dau g hter method s
The chronometric equation with the usual notational conventions is written i n the linear
approximation, with being the radiogenic isotope ratio and the parent^daughter iso-
tope ratio:
¼
0
þ lt
Δt/t
Age (years)
Uncertainty on
14
C
500 5000 10 000 30 000
30%
20%
10%
Figure 5.10 Relative uncertainty on a
14
C age determination as a function of that age. Notice the scale is
logarithmic.
168 Uncertainties and results of radiometric dating

from which
t ¼
1
l
0
:
Theuncertaintiesarethenwritten:
Dt
t
¼
Dl
l
þ
Dð
0
Þ
ð
0
Þ
þ
D
but (
0
) ¼lt, hence:
Dt
t
¼
Dl
l
þ
1
D
lt
þ D
where istheuncertaintyonthemeasurementof,andthatonthe measurementof .
We n ote * ¼
0
. Letus leave aside the uncertainty a¡ecting the d ecay constant. For
agiven radiometric dating method:
Dt
t
¼
D
lt
þ
D
:
Wenoticeimmediatelythatuncertaintyrisesveryquickly whenlt !0.Th erefore each chron-
ometer based on the parent^daughter pair has a lower li mit ofapplicationT
min
.Inallofthe
long-p eriod metho ds we have considered, never tends towards zero. So there is no upper
limit.Al l ofthese chronometerscandate events fromT
min
until theageofthe Universe.
4
Measurement uncertainty is related to the measurement of and , an d again this was
considere dinChapter 1.Therearetwokinds ofmeasurementuncertainty: chemicaluncer-
tain ti es in the preparation stagebecause ofpossible contaminationor poor practicein iso-
topic dilution and physicaluncertaintiesrelatedtothe precision ofthemass spectrometer.
Inpractice, to m inimizethe ¢rstofthese, thereagents arepuri¢ed soas tomake contami-
nation negligible. For the mass spectrometer, we increase the number of measurements to
improvethe statistics, as alreadydescribed.
Exercise
Typically, precision on the measurement of the
87
Sr/
86
Sr ratio is 10
4
and does not vary much
with the ratio, which is about 0.7. The uncertainty on the decay constant is 2 10
2
. Precision
on measurement of the
87
Rb/
86
Sr ratio is not as good because concentrations of elements
must be measured by isotopic dilution (we shall estimate it at 3.5 10
3
). By taking the
example of granite where
87
Rb/
86
Sr ¼3.5, calculate
t
and
t
/
t
as a function of age.
Answer
D
t
t
¼ 2 10
2
þ
1
3:5
10
4
1:4 10
11
t
þ 3:5 10
3
:
Figure 5.11 illustrates the variation of
t
/
t
and of
t
over time.
4
This remark applies neither to radioactive chains nor to extinct radioactivity, because in both these cases
there is a T
min
and a T
max
as in dating methods based on the parent isotope.
169 Sources of uncertainty in radiometric dating

Exercise
Lanthanum-138 decays by electron capture to
138
Ba and by
emission to
138
Ce. The decay
constants are
l
cap
¼4.4 10
12
yr
1
and
l
¼2.255 10
12
yr
1
. (This is a similar situation to
the branched decay of
40
K into
40
Ar and
40
Ca.)
(1) Establish the general chronometric equation and its linear approximation.
(2) Lanthanum-138 represents 0.089% of normal lanthanum. Barium-138 makes up 88% of
naturally occurring barium. The uncertainty on the measurement of the
138
Ba/
137
Ba ratio
is 10
4
for a ratio greater than 6.3997, which is the normal value. This value is the value
of the initial ratio for all rocks and terrestrial minerals.
What must the
138
La/
137
Ba and therefore the La/Ba ratio be for us to use this method to date
rocks 2 10
9
years old (neglecting the uncertainty on
l
) with an uncertainty of less than 2%?
(Notice that if we measure a ratio with a relative precision of 2 10
4
, the absolute
precision on the ratio of 6.4 is about 1.3 10
3
.)
Answer
(1)
138
Ba
137
Ba
¼
138
Ba
137
Ba
0
þ
138
La
137
Ba
l
cap
l
cap
þ l
ðe
ðl
cap
þl
Þ
1Þ:
The linear approximation of this formula is:
138
Ba
137
Ba
¼
138
Ba
137
Ba
þ
138
La
137
Ba
l
cap
t
:
(2) To solve the problem,
138
La/
137
Ba must be roughly equal to 3.6, that is the La/Ba ratio
must be about 557. This is a substantial La/Ba ratio seldom found in nature.
5
Here are a
few ratios for common rocks, to give us an idea: peridotite ¼0.1, granite ¼0.75,
basalt ¼0.5. This is why this method is little used in practice.
100
10
–1
10
–2
10
–3
10
1
Δ
t (Ma)
Δt/t
1 Ga 100 Ma 10 Ma4 Ga
relative uncertainty
absolute uncertainty
Time
Figure 5.11 Variation of absolute and relative uncertainty on the
87
Rb–
87
Sr age of a granite as a
function of its age. For the granite
87
Rb/
86
Sr ¼3.5. Notice that the relative uncertainty declines with
age. Notice too that the age scale is logarithmic.
5
High ratios are found only in a few rather rare minerals such as allanite. This is the mineral used to
determine this date.
170 Uncertainties and results of radiometric dating

5.3.3 Uncertainties on age calculations
After the measurement phase we have either a single measurem ent or a se ri es of measure-
ments. In the ¢rstinstance, we apply the dating formulawhichyieldswhatwehave called an
apparent age and we move on to the next stage which is the geolog ical interpretation. If we
have a series of measurem ents, which is usual ly the case nowadays with the faster methods
ofanalysis available, anyofseveralsituations mayarise.
Case 1. The series of measurements relates to various chronometers on various coge-
netic rich systems.This is the semi-quantitative problem we h ave already addressed.The
age is limited at the lower bou nd by the age of the most retentive mineral, say, the
206
Pb^
207
Pb age on zircon or hornblende if it is K^Ar alone.This situation is nowadays
of historical and didactic interest only, since mo dern studies are made on a set of
measurements.
Case 2.We have many measurements made by one method on one type of mine ral.This
caseisbecom ingever moregeneralwiththedevelopm entofin- situ methodsofanalysis:ser-
ies of
206
Pb^
207
Pb measurements on zircon using an ion probe, series of
39
Ar^
40
Ar or
40
K^
40
Aron micaorbasaltglassusing laser extractiontechniques.
Case 3. A series ofpaired measurements maybe usedto de¢ne a straight-line isochron or
adiscordia.
In the latter two instances, which are n ow the most common, there is a twin problem
to overcome. First, can a valid age be calculated from the values measured? In other
words, do the conditions for applying the theoretical reference models prevail? Is the
alignment acceptable? T his is the issue of acceptabil it y. After answering this ¢rst ques-
tion, how do we calculate the most reliable age mathematically, and with what uncer-
tainty? This is th e age calculation proper. Obviously, the answer may involve both
geological and experimental considerations. We have adopted the following rules. We
s hal l i nt ro d u ce t h e ge olo gi cal c r iter ia at th e sa me t i me as t he acc eptabi l it y cr iter io n ,
but not when calculating the age proper. This means we shall not attribute geological
uncertainties to each sample measured because we have no rati onal mean s of ¢xing them
quantitatively.
We shall therefore calculate ages and their uncertainties from standard statistical meth-
ods on measurements that are geologically accepte d.We then have an age and an uncer-
tainty. We shall then introduce geological uncertainties when making the geological
interpretation.
To return to the example given in the introduction, if we have a series of measurements
plotted in the (
87
Rb/
86
Sr,
87
Sr/
86
Sr) diagram we shall introduce a geological appraisal to
decide whether th e alignment of experimental measurements is acceptable or not and
whether some peculiar measurements must be eliminated (we shall see how to do this with
an objective statistical criter ion). If the answer is positive, we shall c alculate the age using a
weighted least-squares method.
6
We then introduce geological uncertainti es when inter-
preting thegeological ageobtained (Figure 5.12).
6
Thus in the theoretical example in the introduction we use option (c) in Figure 5.1 .
171 Sources of uncertainty in radiometric dating
I ndivi d u al age stati s tic s
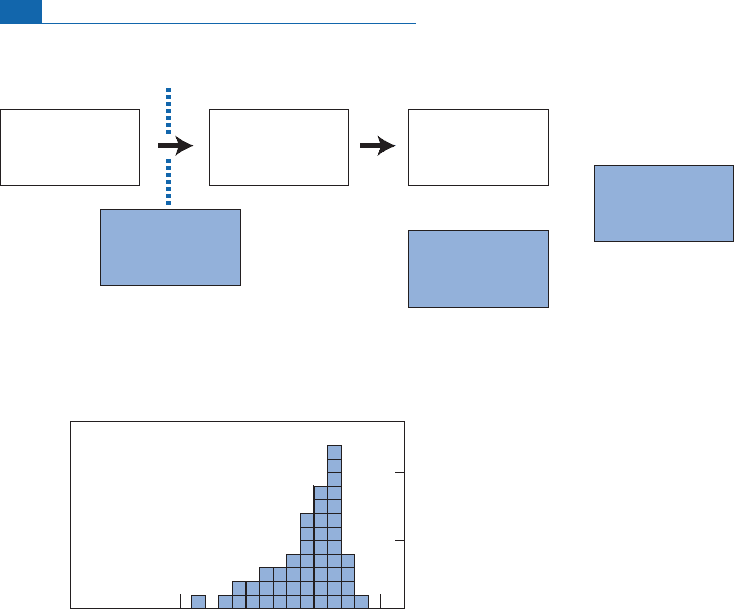
These individual apparent age statistics relate to measurements made on rich systems.The
problemisanalogoustothatofphysical measurements. Forexample,ifwemeasuretheappar-
ent
207
Pb^
206
Pb age on what we think is a cogenetic series of zircon samples, we construct
the histogram ofdata.This distributionwill be generally asymmetrical, with the asymmetry
b eing established towards the you nger agesbecause of the di¡usion of the daughter isotope
which tends to lower the age. From that point, we choose the modal value as the age and the
standard deviation of the distribution as the uncertainty. By way of example, here is a
207
Pb^
206
Pb asymmetrical age distribution obtained by using an ion probe on zircon
(Figure 5.13). But when we analyze detrital zircons in sedimentary rocks, not only grain by
grainbutevenbyseveral measurementsonasinglegrain,thehistogram is extremelycomplex.
Itcanonlybeinterpretedaftergeologicalandquantitativestatisticalanalyses.
Uncertainties in meas uring straight lines of isotope evolution
Presence orabsenceof alignment
We must also know how to estimate the uncertainty on a series of measurements that do
or do not de¢ n e an isochron or a straig ht line on the con cordia diagram.This is what we
Data
Filter
Geological
acceptability
Statistical
processing
Result with
uncertainties
Geological
data
Interpretation
with
uncertainties
}
Figure 5.12 The points in the procedure at which geological knowledge is introduced.
N
Age (Ma)
450 500 550 600
10
5
Figure 5.13 A series of apparent
207
Pb–
206
Pb ages determined on zircon using ion probe spot analysis.
The proposed age is 560 20 Ma.
172 Uncertainties and results of radiometric dating

may call the alignment uncertainty, because for the metho d of the straight line of isotope
evolution as fo r the concordia method, data points are rarely perfec tly aligned and all
the less so as the precision of the experimental method increases.What causes this non-
alignment? A shortcoming in the initial natural isotopic homogenization, that is, at the
tim e the rock crystallized? A slight opening of the system? The choice of samples?
Admitted ly, the mathematical uncertainty can be calculated with a least-squares pro-
gram, which isultimately whatwe do (becausewe knowofno alternative), butisthis areli-
able method? As long as we ignore what caus ed the uncertainty, its meaning remains
ambiguous.
The ¢rst estimate of the alignment or otherwise of data points must be made visually on
the diag rams, making allowance, of course, for the experimental uncertainties attributed
to each measurement. Next we turn to statistical methods as they allow the approach to be
rationalized.
All these words of warni ng are intended to emphasize the fact that there is no auto-
matic process or mathematical formula to be blindly applied. Instead, each step
requires all of the physical, chemical, and geological knowledge available in each
instance.
The correlation coe⁄cient
Let there be two variables (y, x)andaseriesofpairedvalues(y
1
, x
1
), ( y
2
, x
2
), ...,(y
N
, x
N
),
that is, for us, a coupl e of analyses of two isotopic or che mical ratios.We can calculate th e
mean forbothvariables:
y ¼
1
N
X
N
1
y
i
and
x ¼
1
N
X
N
1
x
i
:
We can calculatethevariances relativetothemeanvalues ofx andy:
V
x
¼
1
N
X
ðx
i
xÞ
2
and V
y
¼
1
N
X
ðy
i
yÞ
2
:
Thestandarddeviations, whicharethe squarerootsofthevariances, arewritten
x
¼
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
P
ðx
i
xÞ
2
N
s
and
y
¼
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
P
ðy
i
yÞ
2
N
s
:
Wehaveanalogouslyde¢nedwhatis termedcovariance (alreadyencountered):
V
xy
¼ V
yx
¼
1
N
X
ðy
i
yÞðx
i
xÞ:
Thiscovarianceiszeroifthevaluesofyand x varyindependentlyofoneanother.Ifthevaria-
tions are correlated, the magnitude willbe either positiveor negative dependingonthe sign
of the correlation. This covariance could re£ect the value of the correlation. However, if
itwereleftso, itwoulddependonthe actualvalues ofbothx
i
and
xandofy
i
and
y. Forexam-
ple, it would be di¡erent for a pair of variables measured in ppm and another measured
173 Sources of uncertainty in radiometric dating

in percent wh ere the correlation looked the same.To make the correlation measurement
independent of the units chosen for measuring y and x, we de¢ne the correlation coe⁄-
cientr:
r ¼
P
ðy
i
yÞðx
i
xÞ
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
P
ðy
i
yÞ
2
q ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
P
ðx
i
xÞ
2
q
¼
V
xy
ffiffiffiffiffiffiffiffi
V
yy
p
ffiffiffiffiffiffiffiffi
V
xx
p :
Whenx and yareuncorrelated, r ¼0 ; whentheyarefullycorrelated jrj¼1(þ1forapositive
correlation and 1for a negative correlation).This was the parameter
u, v
used previously
in combiningstatistics.
Exercise
We have a series of
87
Rb–
86
Sr analyses given in Table 5.2. These analyses are plotted on the
diagram in Figure 5.14 as stars. (The white dots are for the next exercise.)
Calculate the coefficient of correlation.
Answer
We posit
87
Sr/
86
Sr ¼
y
and
87
Rb/
86
Sr ¼
x
. The mean values are calculated as:
x
¼ 4 and
y
¼ 0:769 28.
Hence
x
¼2,
y
¼0.0284,
V
xy
¼0.0568, and
r
¼0.9375.
Now, as can be seen (Figure 5.14), the points are not perfectly aligned. If dealing with a
very old age (>2 Ga) we would be tempted to accept this procedure for calculating ages.
For younger ages, we must bear in mind that the result is affected by substantial
uncertainty.
Exercise
We posit
87
Sr/
86
Sr ¼
y
and
87
Rb/
86
Sr ¼
x
. Consider the table of measurements below (Table 5.3).
Calculate the means, standard deviations, covariance, and coefficient of correlation (see
Figure 5.14).
Sample 1 2 3 4 5 6 7
x
i
x
32101 2 3
y
i
y
0.0308 0.0258 0.0208 0.0058 0.0008 0.0342 0.0492
x
i
x
ðÞ
y
i
y
0.0924 0.0516 0.021 0.008 0.0684 0.1476 0.3728
Table 5.2 Series of
87
Rb/
86
Sr analyses
1234567
87
Sr/
86
Sr ¼y 0.800 0. 795 0. 790 0. 775 0. 770 0. 73 5 0. 720
87
Rb/
86
Sr ¼x 7654321
174 Uncertainties and results of radiometric dating

Answer
x ¼ 4:5185;
y ¼ 0:7647.
Hence
x
¼2.5158,
y
¼0.028 633 6,
V
xy
¼0.060 88, and
r
¼0.985.
It can be seen that
r
is closer to 1 than in the previous exercise. This shows us also the
sensitivity of the correlation coefficient to dispersion.
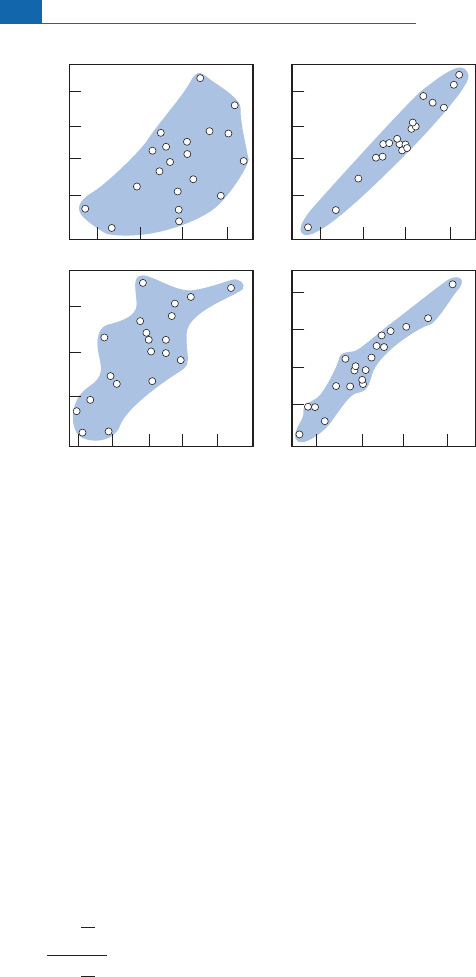
Figure 5.15 shows so me examples of positive correl ations with their correlation coe⁄-
cientsr.
Table 5.3 Further measurements from
87
Rb/
86
Sr analyses
1234567
x 7.1 6.53 6 5.5 3 2.5 1
y 0.801 0.791 0. 785 0.77 5 0. 746 0. 73 5 0. 720
87
Sr/
86
Sr
87
Rb/
86
Sr
0.80
0.75
0.70
2
4 6 8
r = 0.9375
r = 0.985
Figure 5.14 Analyses of
87
Rb–
86
Sr plotted on the (
87
Sr/
86
Sr,
87
Rb/
86
Sr) diagram.
Sample 1 2 3 4 5 6 7
x
i
x 2.5815 2.015 1.4815 0.9815 1.518 2.0185 3.5185
y
i
y 0.0363 0.0263 0.0203 0.0103 0.0187 0.0297 0.0447
x
i
xðÞy
i
yðÞ0.0937 0.0529 0.02398 0.010 10 0.002839 0.05994 0.1572
175 Sources of uncertainty in radiometric dating
Remark
In practice, when the coefficient of correlation is less than 0.90 we consider the data points are
poorly aligned. We do not attempt to identify a straight line. We are outside the conditions accepted
for the various models: no initial isotopic homogeneity, complex opening of the system, etc. If
r
> 0.90 we calculate the parameters of the straight line of best fit by the least-squares method.
In clusion ofexp er i mental un cer taintie s
In these calculations wehave ignoredthe individual experimental uncertainties. Implicitly
we have considered they were all equal. In practice, when these uncertainties vary between
measurements, we must weight them and make allowance for them. Let us take the mean
value
x as an example.
Insteadofsimplycalculatingthe meanby
x ¼
P
x
i
=N,weweightitallowingforvariance:
x
¼
P
i
x
i
2
i
P
i
1
2
i
:
Let us take a simple example.We have three very di¡erent measurements of uncertainty:
3 0.1; 4 2, and 2.5 0.1. If we make the usual calculation,
x ¼ 3:16.Ifwemakethe
weighted calculation
x
T
¼ 551=200:25 ¼ 2:75. There is a 14% di¡erence between the
results.
The variance ofuncertainty (here it is a‘‘true error’’) committed is
2
¼
P
2
i
1
,or
¼0.07 and
x
T
¼ 2:75 0:07.
If all the uncertainties are identical, the variance is
2
x
¼
2
i
=N.We ¢nd D ¼
i
=
ffiffiffiffi
N
p
again.
m+2σm-2σ m
r = 0.500
m+2σm-2σ m
r = 0.750
m+2σm-2σ m
r = 0.980
r = 0.950
m+2σm-2σ m
Figure 5.15 Measurements that are more or less closely correlated with various values for the
corresponding correlation coefficient.
176 Uncertainties and results of radiometric dating
