Алексеев В.В. Физическое и математическое моделирование экосистем

Подождите немного. Документ загружается.

терными

для

экологической группы

целом. Используя отклоне-

ния

от

средних значений коэффициентов

качестве малых пара-

метров, можно построить кинетические уравнения

для

описания

динамики трофических уровней (трофических групп) экологиче-

ских систем

[18, 62].

Уравнения для трофических уровней двухуровневой

вольтер-

ровской системы.

Рассмотрим сначала случай построения кинети-

ческих уравнений

для

двухуровневой системы вольтерровского

типа, динамика видов которой описывается следующей системой

уравнений:

42)

где

М* —

биомасса

1-го

вида жертв;

—

биомасса

ft-го

вида

хищников;

1 и е

х —

соответственно коэффициенты рождаемо-

сти жертв

смертности хищников;

у" —

коэффициент потребления

хищниками жертв;

j —

коэффициент перехода (усвоения)

био-

массы жертв

биомассу хищников;

п и т —

число видов хищни-

ков

жертв соответственно.

Все

коэффициенты считаются посто-

янными

положительными величинами.

Как

правило,

j ^ ау£',

где

а < 1

(обычно

а =

0,1...

0,2), т. е.

только часть съеденной

пищи

переходит

биомассу хищника. Будем считать,

что

коэффи-

циенты системы

(8.42)

можно представить

виде

где

аБ

ж.

аБ

х —

Гж

тп

i=l

1=1

тп

. ,

Предположим,

что

различия

коэффициентах видов

пределах

экологической группы являются малыми

по

сравнению

со

сред-

ними

значениями параметров группы

(8.44)

271

Поставим

задачу перехода от уравнений для биомасс отдель-

ных видов к уравнениям для «макроскопических» переменных,

т. е. для биомасс экологических групп (трофических уровней)

Е Zi.

(8.45)

Подставляя (8.43) в (8.42) и производя суммирование по всем

видам, входящим в соответствующие трофические уровни, полу-

чим

+ Е

Де

- Е Е

" " ' [=1 " ~ «="l /="1 ,g 4

rfM

Здесь

= е

—-у

ж>

= —е

VxM

(8.47)

Из

(8.46) нетрудно видеть, что в нулевом приближении по раз-

бросу коэффициентов уравнения для трофических уровней перехо-

дят в классические уравнения В. Вольтерра для системы «хищ-

ник—жертва». Чтобы получить более точные уравнения, продиф-

ференцируем (8.46) по времени и подставим вместо производных

№

и М

ИХ значения из уравнений (8.42). В результате, прене-

брегая величинами второго порядка малости по разбросу

коэффи-

циентов

и используя (8.46), получим

= -^ (М

) + М

(М

- М

) + М

-М

ЕДе

(8-48)

-м

»-'"'

Теперь нетрудно избавиться от величин ]

2 Ле

' М' , продифференцировав (8.48) еще раз по времени, а за-

тем используя выражения (8.46) и (8.48). Введем обозначения

= М

- \±г (М

) + (М

- М

) (М

+ М

)1,

«а • - - - 1

)

= Мх —

—гг

(М

)

+ (М

— М

) (М

+ М

) .

272

Используя

(8.49), уравнения (8.48) можно записать в виде

^ж = — Z АЁЖМЖМЖ,

(

°)

Дифференцируя

(8.50), получим

— М

LxMx/M,

Y, ж

(8-51)

Здесь мы пренебрегли малыми второго порядка после использо-

вания

уравнений (8.46). Окончательно уравнения для трофиче-

ских уровней после замены сумм их выражениями из

(8.50)

будут

иметь вид

В общем случае, чтобы получить уравнения для макроскопи-

ческих величин, т. е. для трофических уровней, из уравнений для

микроскопических величин, т. е. уравнений для видов, необходимо

последовательно провести замену одних функций времени М'

(t)

' (t) на

другие

функции:

, М

, М«, ....

bAjdt

, М

х>

....

Mjd<

Для определения стационарных состояний из

(8.52)

получаем

уравнения

МхМ

(М

+ М

) = 0,

_, _ -

(о.

53)

(М

+ М

) = 0,

т. е. М

= 0 и М

= 0, что соответствует стационарным состоя-

ниям

нулевого приближения по разбросу коэффициентов. Иссле-

дуем

решения уравнений

(8.52)

вблизи стационарных состояний:

/у

+ м-. M

e«/Y«

+ v,

(8.54)

где ц и v — малые добавки (по сравнению с величинами стацио-

нарных биомасс трофических уровней). Из

(8.47)

находим

YxH'>

=—

у.

(8.55)

Так

как М

/М

и М

/М

имеют нулевой порядок малости соответст-

венно по ц и v, a L

и L

— первый порядок малости, то вторыми

18 Заказ № 57 273

членами в правой части (8.52) можно пренебречь. Тогда (8.52)

легко интегрируются, и мы

будем

иметь

1ж = ДМ

, L

= 5M

, (8.56)

где А и В— постоянные интегрирования. Сравнение уравнений

(8.56) и (8.50) показывает, что

= - Z

Ae«ML,

5 = Е Ае'М

. (8.57)

Используя (8.49), (8.54) и (8.55), запишем (8.56) в виде

Лу

ц,

lo.ooj

V —

Система линейных уравнений (8.58) может быть легко проинте-

грирована. Из второго уравнения (8.58) получаем

* + Ву

ч). (8.59)

Дифференцируя

первое уравнение (8.58) и подставляя ц из (8.59),

получим

v + (Ву

- Ау

)

v -

АВу

= 0. (8.60)

Характеристическое уравнение для (8.60) имеет вид

+ (Ву

- Ау

ех

) V —

АВу

= 0.

Корнями

этого уравнения

будут

Я-1.

з, з.

= ± {-

(exe»

+ Ву

— Ау

)/2 ±

[(exe«

+ Ву

- Ау

у/2 + АВу

)

}

(8.61)

Необходимо отметить, что

учет

второго приближения по Де и Ду

приводит к тем же значениям характеристических частот. Таким

образом, динамика биомассы трофических уровней в исследуемом

случае может быть описана суммой

двух

колебаний — быстрого

медленного. Для того чтобы проиллюстрировать процесс нало-

жения

колебаний различных масштабов, на ЭВМ была решена

конкретная

система уравнений для шестивидовой трофической си-

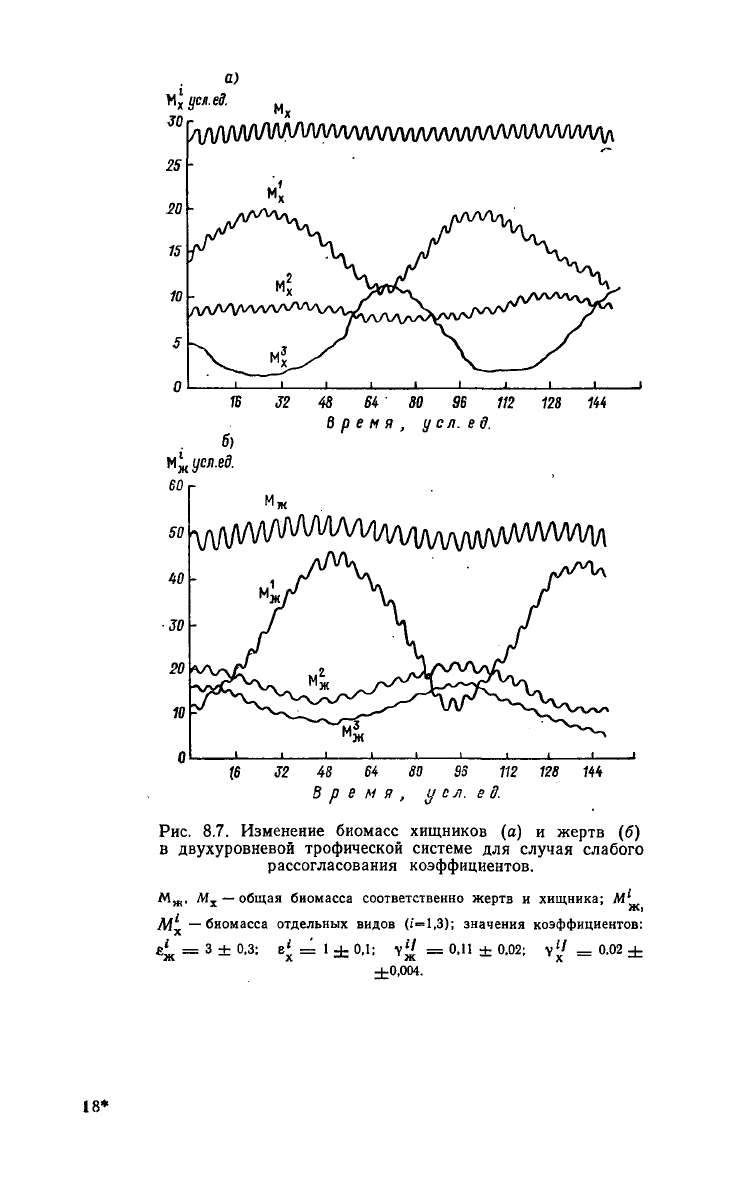
стемы. На рис. 8.7 показана динамика биомасс трофических уров-

ней

жертв и хищников, а также динамика биомасс видов, слагаю-

щих эти уровни. Отчетливо видны два характерных периода ко-

лебаний.

Если привести данный пример к масштабу времени, на-

блюдаемому в реальных водоемах, то быстрые колебания

будут

давать изменения биомасс в течение сезона (период этих колеба-

ний

составляет несколько месяцев), в то время как медленные ко-

лебания

отдельных видов показывают, что из нескольких близких

видов организмов отдельные виды

могут

в течение ряда лет на-

ходиться в подавленном состоянии, но иногда давать значитель-

274

MJJ

уся.ед.

/\pj\l\l\l\l\N\J\f\NW\^^

б)

усл.ед.

48 64 80 9E 112 128

Время,

у ел. ев.

во

•

(в

32 48 64 80 93 112

Время,

с л.

д.

128

1Н

Рис.

8.7. Изменение биомасс хищников (а) и жертв (б)

двухуровневой трофической системе для случая слабого

рассогласования коэффициентов.

—

общая биомасса соответственно жертв

хищника;

М —биомасса отдельных видов

(£—1,3);

значения коэффициентов:

3 ± 0,3; е' =

14-0,1;

< = 0,11 ± 0,02;

=0,02±

±0,004.

18*

ную биомассу.

Из

рисунков видно,

что

медленные частоты одина-

ковы

для

всех

видов

совпадают

медленными частотами

для

трофических уровней. Ниже

будет

показано,

что

этот

результат

справедлив

не

только

данном частном случае,

но и при

произ-

вольном числе видов

на

уровне.

Динамика видов двухуровневого вольтерровского

биоценоза.

Будем рассматривать систему уравнений

(8.42)

ограничениями

на

коэффициенты (8.43). Перейдем

(8.42)

отклонениям

от

стационарного состояния

м^

+ цЦ

м<

iii)- (8-62)

Если

M'L<

И-

'<1.

то

(8.63)

Дифференцируя

первое уравнение

(8.63)

по

времени

подстав-

ляя

него затем

\i\. из

второго, получим

+ t

[(А

)

И*

+ ТгМ -

О,

Л(%,

J—

/ — *

Уравнение

для

нахождения характеристических чисел имеет

вид

Я,

(А

+ В

)

+ T

(8.65)

где

i —

индекс строк;

k —

индекс столбцов.

Проделаем

определителем

(8.65)

следующие операции:

выч-

тем

из

первой строки вторую,

из

второй третью,

из

третьей четвер-

тую

и т. д.; в

полученном определителе прибавим первый столбец

ко

второму, новый второй столбец

третьему

и т. д.,

затем выне-

n-i

сем из-под знака определителя множитель

П (5' —

i+i

разде-

лив каждую

i-ю

строку

от

первой

до (п — 2)

соответственно

на

(В'

—

i+i

);

затем вычтем

из

первой строки вторую,

из

второй

третью,

..., из (п —

2)-й—(п—1)-ю. Заметим,

что

если

для ка-

кой-либо

строки окажется,

что

разность

В' —

i+i

= 0 (или

имеет

второй порядок малости),

то с

этой строкой

не

надо производить

больше никаких операций, поскольку

она уже

приведена

к нуж-

ному

виду.

Далее вынесем

за

знак определителя множитель

276

m-1

(В' —

i+i

умножив

при

этом каждый

t-й

столбец

на

г=1

(В'

—

В'+>)

от

первого

до (п)

столбца соответственно.

получив-

шемся

определителе прибавим первый столбец

ко

второму,

но-

вый

второй столбец

третьему

и т. д. до (п—1)

столбца вклю-

чительно. Если пренебречь членами третьего порядка малости

по

разбросу коэффициентов,

то в

результате

получим

п-2 Г / k 2

л V (RI

F>i

V n' _L

= i s=i В — В

— 1 / -р г«

в-'-в»

+ Z г„.

5=1

Решая

последнее уравнение, получим

k 2

г г

= 1, 2

(п-2),

^ —

ухУж

<2ж

£ Qx «

1=1

Отсюда видно,

что

виды колеблются

двумя характерными

ча-

стотами, соответствующими быстрым

медленным колебаниям

биомасс трофических уровней.

Уравнения

макродинамики

экосистем

произвольным

числом

трофических

групп.

Рассмотренный выше метод построения

кине-

тических уравнений

для

биомасс трофических уровней допускает

обобщение

для

более реалистичных моделей многовидовых

эко-

систем. Пусть система уравнений, описывающих динамику

био-

масс отдельных видов экосистемы, имеет

следующую

форму:

^дд? п «б

_-L

e?Mf

p?Mi

Zv^MfM,

a=l,

я, 1=1, п

6 = i/=i

(8.66)

где М

—биомасса

i-ro

вида трофического уровня (группы)

а;

е?

—

коэффициенты смертности видов;

—

коэффициенты фото-

277'

синтеза продуцентов (для консументов этот коэффициент равен

нулю); у

!* — коэффициенты взаимодействия

между

видами раз-

личных трофических групп (предполагается, что У?? = 0); Мо —

концентрация

лимитирующего биогенного элемента в среде; п —

число трофических групп в системе;

Па.

— число видов в трофиче-

ской

группе а. Коэффициенты модели в общем

случае

могут

за-

висеть от внешних абиотических факторов (температуры, освещен-

ности

и др.) и меняться во времени.

Для широкого класса экосистем круговорот биогенных элемен-

тов является замкнутым:

Z М? + М

= M

= const. (8.67)

a=l

i = l

Для описания проточных систем необходимо задать закон измене-

ния

концентрации лимитирующего биогенного элемента в среде

Mo(t) как функцию времени.

Предположим, что различия в коэффициентах видов в преде-

лах экологической группы являются малыми по сравнению со

средними значениями параметров группы

е?

= е

Де?,

р? = Р« + Др?,

(8.68)

аб . . аб

Y Y + AY

где

|Ле?|<е

а>

Поставим

задачу

перехода от уравнений для биомасс видов M°f

уравнениям для биомасс экологических групп Ma™ S М?.

Подставив

(8.68)

(8.66)

и произведя суммирование по i до п

получим

Ра„

+ £

в^ 1

-\-c

S Ь

аЬ

2 AefM?, (8.69)

"а »б

278

Нетрудно видеть, что уравнения для экологических (трофических)

групп

(8.69)

отличаются по форме от уравнений для отдельных

видов членами а

, с

, Ь

в, отражающими разброс коэффициентов

видов. Уравнения для экологических групп совпадают с уравне-

ниями

для видов, только если разброс коэффициентов равен

нулю. При этом в нулевом приближении (без

учета

разброса па-

раметров) получаем

М? (О = М

(t) М? (0)/М

(0),

(8.70)

т. е. как это и следовало ожидать, биомассы видов изменяются

во времени и синхронно с биомассой экологической группы, если

их коэффициенты одинаковы.

Дифференцируя

, с

, Ь

в по времени и используя разброс

коэффициентов

в качестве малого параметра, с

учетом

(8.66)

(8.70), с точностью до членов третьего порядка малости по раз-

бросу коэффициентов получим

ИФ

* = ^аМа + п

+ С

+ £ ^аб>

"' 6=1

"а.

(dMo/dO/Mo]

dt —V*

(8.71)

n "a

Д?? = Ae? + ApfMo + Z

Z A

M/•

Уравнения

(8.71)

представляют собой замкнутую систему уравне-

ний

для биомасс трофических групп (уровней) многовидовой эко-

системы. Эта система имеет существенно меньшую размерность,

нежели исходная система уравнений

(8.66)

для биомасс видов.

случае

двухуровневой экосистемы, например, для описания

биомасс трофических уровней, имеем всего семь уравнений

(8.71),

тогда

как система, описывающая динамику видов, мо-

27»

жет включать в себя сотни и даже тысячи уравнений. Исследуем

уравнения

(8.71)

на примере двухуровневой модели. Вблизи поло-

жения

равновесия М

= Ма + т

, где т

— отклонения от равно-

весных значений биомасс М

. Линеаризуя (8.69) то т

и диффе-

ренцируя затем dm

/dt по времени, систему

(8.71)

можно преоб-

разовать к следующему виду:

-(Pi

+ APi) Mi

dmi/dt

— (Y

AYI

+ В

—

(Y12 + PI + Api) Mi

fdt,

(8.72)

= Y

dmjdt

— (Pi

+ B) Mi M

mi —

—

[(YI2

+ Pi) Ау

+ В + B

] MiM

где

Др,

= £

Z Z

Y''/

Pi<p2/,

AYTAPT

=| |

= AY12 AY

= Z Z I AY<'

AY«

PHPUP2/,

«I «2 П

Здесь Mi,-, M

- — стационарные значения биомасс видов; р

- =

Mi,/Mi;

/ =

/М

Нетрудно убедиться, что для характеристического уравнения

имеет место выражение

+ (Pi + Ар,) М^

+ Mi M

[v2i (Y12 + PI + ^Yi2 + Api) +

(Y12 + Pi) Дуяг +B + B

{

+ M?M

(P1P2 +

Yi2 APi

— V12B) I + M?M

2Y2

i (Y12 + PI)

A~YI

= 0. (8.73)

Исследуя (8.73) по критерию Раусса—Гурвица, находим, что ста-

ционарное

решение системы для биомасс трофических уровней

является устойчивым, если выполняются неравенства

AY12 AY21 > 0.

(8.74)

(AY21

AYIS

— AY21 AY12) > Y'2 0

280