Алексеев П.Г., Гаврилова Е.В., Гольцова И.Г. Тепловые процессы
Подождите немного. Документ загружается.


- 41 -
Определим ориентировочную поверхность теплообмена:
3
2
ОР
ln
ОР СР
Q 953,17 10
F 40,79
м .
700 33,38
K Δt
_
По каталогу выбираем F
ОР
ТА с таким расчётом, чтобы скорость дви-
жения воды w, определяемая из соотношения G
В
= ρ
В
F
ТР
w, была достаточной,
чтобы Re > 2 × 10
3
.
Выбираем ТА с F > 43 м
2
, d = 25×2 мм, l = 6 м, 4
х
-ходовой.
F
ТР
= 0,034 м
2
. На один ход приходится:
3 2
ТР
ТР
F
0,034
F 8,5 10
м .
4 4
_
В
3
В ТР
G
7,58
w 0,894
м/с.
ρ F
997 8,5 10
_
3
7
wd 0,894 0,021
Re 20407 2 10 .
ν
9,2 10
Определим коэффициент теплоотдачи:
0,25
0,8 0,43
t
θ
Pr
Nu 0,021Re Pr ;
Pr
Т. к. θ неизвестна, то принимаем
0,25
t
θ
Pr
1.
Pr
0,8 0,43
Nu 0,021 20407 6,22 1 129,23.
2
2
Nu
λ 129,23 0,608
α 3742 Вт/ м ×
К .
d
2,1 1
_
0
К расчёту интенсивности теплообмена при конденсации бензола:
33 2 3 2
4 4
4 2
λ ρ rg 0,14 834 408,5 10 9,80665
A 0,72 0,72 3810.
μd
3,9 10 2,5 10
Необходимо ввести поправку на рядность: ε
n
= 0,58.
Коэффициент теплопередачи K рассчитываем методом итерации, начи-
ная с K
ОР
= 700 Вт/(м
2
×К).
1
1
1
1
ln 3
1 1
3
3
СР
3 3
НОВ1 ОР
4 4
2
3 3
n
Δt
δ 1 33,4 2 10 1
K K 700
λ α 40 3742
A ε 3810 0,58
= 872,81 Вт/(м
2
×К).
1
1
1
1
ln 3
1 1
3
3
СР
3 3
НОВ2 НОВ1
4 4
2
3 3
n
Δt
δ 1 33,4 2 10 1
K K 872,81
λ α 40 3742
A ε 3810 0,58
= 827,16 Вт/(м
2
×К).
Проводим итерацию, получая всё более близкое к действительному
значение коэффициента теплопередачи. В итоге имеем следующие результа-
ты:
www.mitht.ru/e-library
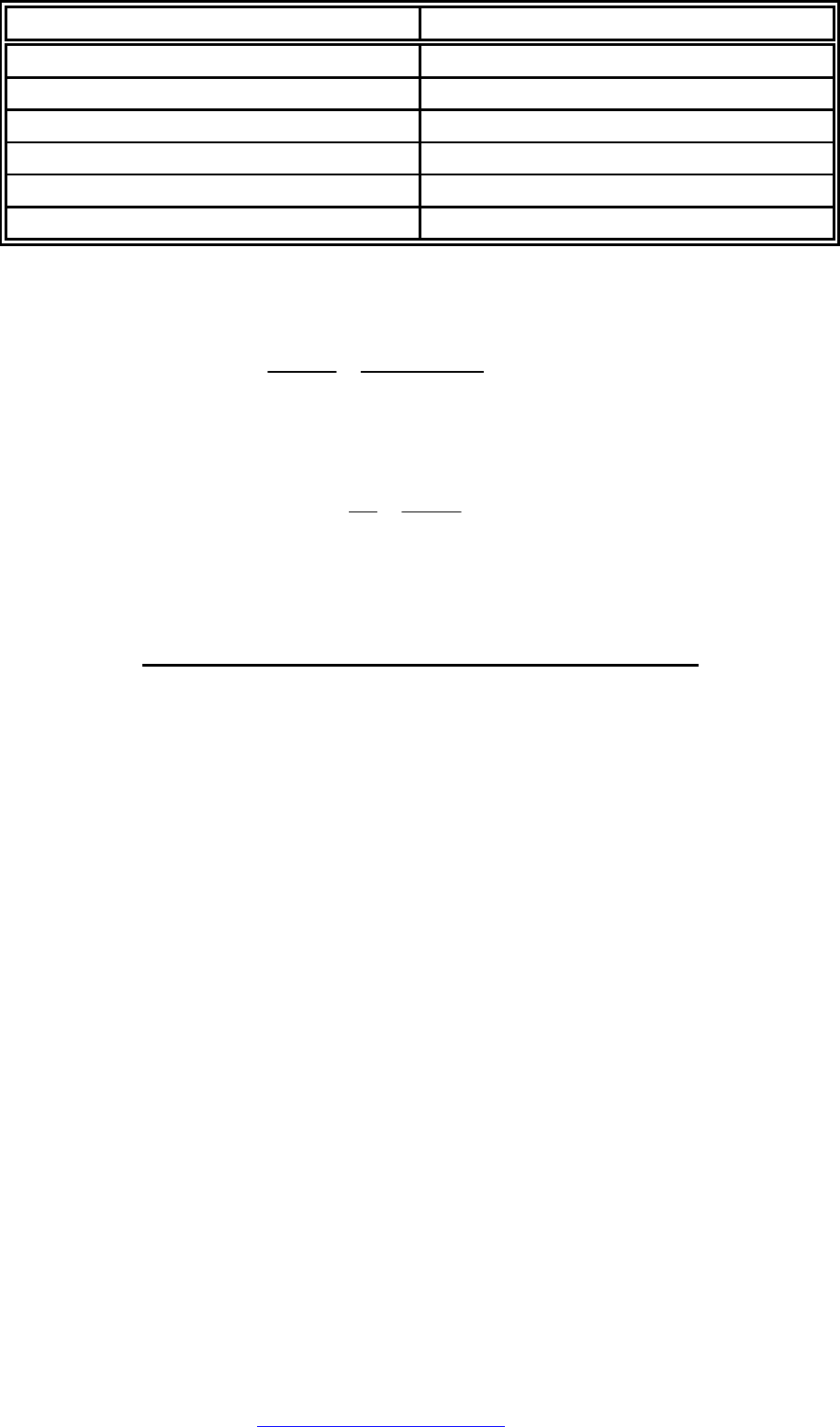
- 42 -
K
СТАР
K
НОВ
700 872,81
872,81 827,16
827,16 838,13
838,13 835,43
835,43 836,09
836,09 835,93
В итоге получаем значение коэффициента теплопередачи:
K = 835,9 Вт/(м
2
×К).
Расчётная поверхность теплообмена равна:
3
2
ln
СР
Q 953,17 10
F 34,14
м .
835,9 3 ,4
K
_
3
Δt
Выбираем по каталогу: 4
х
-ходовой ТА с F
К
= 39 м
2
, F
ТР
= 0,034 м
2
, n
ТР
=
= 100, n
Р
= 12, ε
n
= 0,63, l = 5 м.
Коэффициент запаса:
К
F
39
1,14.
F 34,14
Таким образом, расчёты показали, чтобы обеспечить технологический
процесс конденсации бензола, необходим ТА с вышеуказанными параметра-
ми.
Глава 7. Тепловой расчёт выпарной установки.
Выпариванием называется процесс концентрирования раствора неле-
тучих веществ, заключающийся в частичном удалении растворителя путём
испарения или кипения. Получаемый в процессе выпаривания раствор
называют упаренным, а отводимый пар растворителя – вторичным па-
ром. Обычно удаляют часть растворителя, чтобы раствор находился в теку-
чем состоянии и его можно было бы передавать на другие аппараты.
Целью теплотехнического расчёта выпарной установки является опре-
деление: расхода греющего (первичного) пара, поверхности теплообмена и
основных размеров аппарата и выявление режимных характеристик процесса
(температуры, давления, концентрации и пр.).
Важнейшим параметром выпаривания является температура кипения
раствора t
К
, которая в значительной степени зависит от природы растворён-
ного твёрдого вещества. Разность между температурой кипения раствора t
К
и
температурой кипения чистого растворителя t
S
при одинаковом давлении на-
зывается температурной депрессией: δ
T
= t
К
– t
S
для раствора данной кон-
центрации a. Температура вторичного пара близка к t
S
и обозначается
θ = t
К
– δ
T
.
В химической промышленности наиболее широкое распространение
получили выпарные установки поверхностного типа, которые по теплотехно-
логическим признакам разделяются на несколько групп:
1. по числу ступеней: одноступенчатые и многоступенчатые выпарные
установки;
2. по давлению вторичного пара в последней ступени: выпарные установ-
ки с глубоким вакуумом, с повышенным давлением и с ухудшенным
вакуумом;
www.mitht.ru/e-library
- 43 -
3. по подводу первичной теплоты: выпарные установки с одним источни-
ком первичной теплоты, с двумя источниками теплоты и с тепловыми
насосами;
4. по технологии обработки раствора: одностадийные выпарные установ-
ки, двух- и более стадийные;
5. по относительному движению греющего пара и выпариваемого раство-
ра: прямоточные выпарные установки, противоточные, с параллельным
питанием корпусов, с отпуском части вторичных паров, со смешанным
питанием корпусов.
При проектировании и эксплуатации выпарных установок возникает
необходимость в решении следующих основных групп задач:
1. выбор конструкций аппаратов и схемы установок, определение опти-
мальных параметров разрабатываемых установок;
2. определение оптимального режима работы действующих установок,
обеспечивающего необходимую производительность установки, каче-
ство готового продукта и другие показатели.
При решении этих задач используются проектные и поверочные расчё-
ты. Основной целью проектных расчётов является определение конструктив-
ных параметров аппаратов выпарных установок при выбранных условиях те-
плового режима их работы. При выполнении поверочных расчётов дейст-
вующих выпарных установок основной целью является установление опти-
мального режима работы при заранее известных конструктивных параметрах
аппаратов.
Методы расчёта выпарных установок.
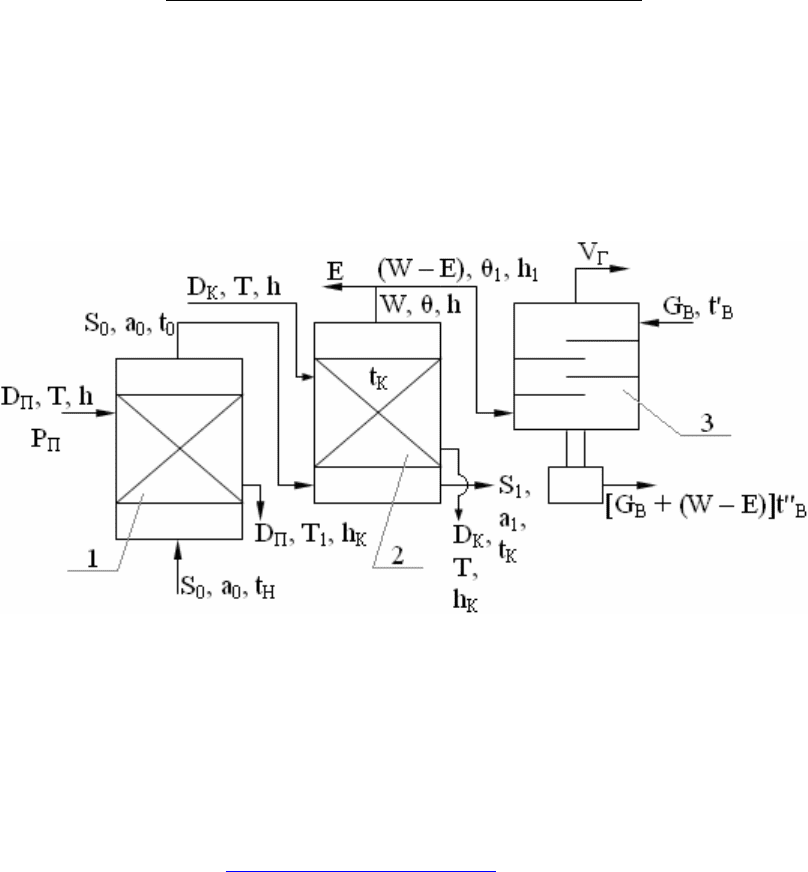
Однокорпусная выпарная установка (рис. 7.1) состоит из подогревателя
1, где исходный раствор (S
0
, a
0
, t
Н
), за счёт греющего пара (D
П
, T, h) нагрева-
ется до состояния (S
0
, a
0
, t
0
) (t
0
≈ t
К
) и поступает в корпус выпарной установки
2. Здесь раствор за счёт греющего пара (D
К
, T, h) (обычно для подогревателя
и 1 корпуса используется греющий пар одних и тех же параметров) доводит-
ся до состояния кипения t
К
= t
S
в результате чего часть растворителя превра-
щается в пар, называемый вторичным (W, θ, h) и отводится из корпуса.
Рис. 7.1.
Однокорпусная выпарная установка.
Часть этого пара E, называемая экстра-паром, используется на произ-
водственные нужды, а остальная часть [(W – E), θ
1
, h
1
] поступает в баромет-
www.mitht.ru/e-library
- 44 -
рический конденсатор смешения 3 (смесительный ТА), где, контактируя с
водой, конденсируется, образуя вакуум.
Упаренный раствор (S
1
, a
1
, t
К
) отводится из аппарата. Также отводятся
конденсаты из обоих корпусов: первого (D
П
, T
1
, h
К
) и второго (D
К
, T, h
К
).
Расчёт выпарной установки, состоящей из трёх узлов, осуществляется
последовательно, начиная с первого корпуса. В основе лежат уравнения: теп-
лопередачи, теплового и материального баланса.
S
0
= S
1
+ W; (7.1)
S
0
a
0
= S
1
a
1
. (7.2)
После преобразования уравнений (7.1) и (7.2) получаем формулу для
определения количества выпаренного растворителя:
0
0
1
a
W S 1 .
a
(7.3)
Уравнение теплового баланса составляется по принципу «приход =
= расходу»:
D
К
h + S
0
C
0
t
Н
= S
1
C
1
t
К
+ D
К
h
К
+ Wh + Q
0
. (7.4)
Используя правило линейности:
S
0
C
0
= S
1
C
1
+ C
В
W, (7.5)
делая подстановку и группировку членов уравнения (7.4), без учёта потерь в
окружающую среду (Q
0
= 0), получаем расчётное уравнение:
Q = D
К
(h
Г
– h
К
) = S
0
C
0
(t
К
– t
0
) + W(h
1
– C
В
t
Р
). (7.6)
Количество греющего пара D
К
находим по уравнению:
В Р
0 0 К 0
К
Г
К
S C t t W h C t
D .
h h
(7.7)
Поверхность теплообмена F
ОР
определяем из уравнения:
Q = KΔt
СР
F, (7.8)
предварительно рассчитав величину Δt
СР
и задавшись значением K
ОР
.
Далее по F
ОР
выбираем выпарной аппарат и его конструктивные разме-
ры: H, d
Н
/d
ВН
, Z – число ходов, n – число трубок, рядов и др. Это, так назы-
ваемые, предварительные размеры аппарата. Окончательные (расчётные)
размеры поверхности теплообмена F определяются методом итерации из
уравнения:
4
0,33
3
1 0,7
К
0b
3
1 1 Q Qδ 1 1 Q
F .
T t A λ B
F
F
(7.9)
Сравнивая F и F
ОР
, определяем степень приближения и при значитель-
ном расхождении (более 10 %) делаем перерасчёт.
Подогреватель исходного раствора 1 рассчитывается как ТА, в котором
конденсирующимся паром нагревается исходный раствор.
Расчёт барометрического конденсатора смешения 3 заключается в оп-
ределении расхода охлаждающей воды G
В
, количества неконденсирующихся
газов V
Г
, мощности вакуум-насоса для их откачки и геометрических разме-
ров аппарата, и базируется на уравнении теплового баланса, Бернулли,
сплошности.
Процесс выпаривания является весьма энергоёмким процессом, тре-
бующим значительного расхода греющего пара (1 кг греющего пара пример-
но равен 1 кг вторичного пара), поэтому для его уменьшения широко исполь-
зуют многокорпусные выпарные аппараты, состоящие из ряда однокорпус-
ных аппаратов последовательно соединённых между собой. Наиболее широ-
www.mitht.ru/e-library

- 45 -
кое распространение получили трёхкорпусные выпарные аппараты с равны-
ми поверхностями теплообмена.
Задачи для самостоятельной работы.
Задача 7-1. Рассчитать двухкорпусную выпарную установку с подогре-
вателем исходного раствора и барометрическим конденсатором смешения
при следующих исходных данных:
1. выпариваемый раствор: KNO
3
;
2. производительность: S
0
= 9000 кг/ч;
3. начальная концентрация растворённого вещества: a
0
= 8 % масс.;
4. конечная концентрация растворённого вещества: a
К
= 48 % масс.;
5. температура раствора на входе в подогреватель: t
0
= 15 °C;
6. температура раствора на входе в первый корпус: t
Н
= t
К1
;
7. давление во втором корпусе (вакуум): P
2
= 660 мм. рт. ст.;
8. количество экстра-пара, отбираемого из первого корпуса: E = 800 кг/ч;
9. давление греющего пара: P
П1
= 4 ата;
10. температура охлаждающей воды: t'
В
= 12 °C.
Пример 7-1.Рассчитать однокорпусную выпарную установку непре-
рывного действия, работающую под вакуумом. Исходные данные:
1. выпариваемый раствор: CaCl
2
;
2. производительность по исходному раствору: S
0
= 3,125 кг/с;
3. начальная концентрация CaCl
2
: a
0
= 18,8 % масс.;
4. конечная концентрация CaCl
2
: a
2
= 60 % масс.;
5. давление в сепараторе аппарата: P
1
= 8 кПа;
6. температура исходного раствора на входе в аппарат равна его темпера-
туре кипения t
Н
= t
К
;
7. давление греющего пара: P
П
= 2,8 ата;
8. гидравлическая депрессия вторичного пара: δ
Г
= 1,5 °C;
9. температура охлаждающей воды на входе в конденсатор: t'
В
= 17 °C;
10. давление парово-газовой смеси на выходе из вакуум-насоса: P
Г
=
= 1,05 ата.
Решение. Справочные данные.
Греющий пар и его конденсат: температура греющего пара – T =
= 130,4 °C; энтальпия греющего пара – h
Г
= 2719 кДж/кг; энтальпия конден-
сата пара – h
К
= 548 кДж/кг; теплопроводность конденсата – λ
К
=
= 0,68 Вт/(м×К); плотность конденсата – ρ
К
= 935 кг/м
3
; теплота парообразо-
вания – r = 2170 кДж/кг; вязкость конденсата – μ = 1,96 × 10
–4
Па×с.
Раствор CaCl
2
: температура кипения при P = 1 ата –
СТ
К
t 142,1 ;
_
°C
вяз-
кость при P = 1 ата – ν = 3,1 × 10
–7
м
2
/с.
Вторичный пар: температура при P
1
= 8 кПа – θ
1
= 41,1 °C; энтальпия –
h
1
= 2578 кДж/кг.
Вода: упругость паров воды при t
К
= 142,1 °C – P'
3
= 3,92 × 10
5
Па; вяз-
кость при P = 1 ата – ν
В
= 2,95 × 10
–7
м
2
/с.
Конструкционный материал: сталь марки – ОХ18Н5Т; теплопровод-
ность – λ = 17,2 Вт/(м×К).
Расчёт корпуса ВУ.
Схема установки приведена на рис. 7.1, а с обозначениями характери-
стик процесса теплопереноса в ВА показан на рис. 7.2.
www.mitht.ru/e-library

- 46 -
Рис. 7.2.
К определению средних температур стенок трубок.
Температура кипения упаренного раствора определяется по правилу
Бабо. Упругость паров воды при температуре кипения t
К
:
S
5
3 4
S 1
4
t
S
P 3,92 10
P P 8 10 3,2 10
Па.
P
9,81 10
_
Температура кипения раствора по правилу Бабо:
S
S К
t
при P t 74,8 °C
_
.
_ _
Поправка Стабникова:
Δ = – 3,6 °C.
Рабочая температура кипения раствора:
t
К
= 74,8 – 3,6 = 71,2 °C.
Температурная депрессия:
δ
Т
= t
К
– θ = 71,2 – 41,1 = 30,1 °C.
Полезная разность температур:
Δ
ПОЛЕЗ
= T – θ – δ
Т
– δ
Г
= 130,4 – 41,1 – 30,1 – 1,5 = 55,7 °C.
Количество выпариваемой воды:
0
0
1
a
18,8
W S 1 3,125 1 _2,146
кг/с.
a 60
Тепловая нагрузка:
Q = S
0
C
P
(t
К
– t
Н
) + W(h
1
– C
В
t
К
) = W(h
1
– C
В
t
К
) = 2,146 × (2578 – 4,19 × 71,2) =
= 4892 кВт.
Ориентировочная поверхность теплообмена:
3
2
ОР
4
Q 4892 10
F 122,3
м .
q
4
_
10
Подбираем поверхность теплообмена по табличным данным:
F = 122 м
2
; d = 38×2 мм; H = 4 м.
Комплекс теплофизических характеристик конденсата греющего пара:
33 2 3 2
4 4
4
λ ρ rg 0,68 935 2170 10 9,80665
A 0,943 0,943 8764.
μH
1,96 10 4
Комплекс теплофизических характеристик кипящей воды:
B
0b
= 46P
0,57
= 46 × 0,08
0,57
= 10,90.
Относительный коэффициент теплоотдачи к кипящему раствору:
www.mitht.ru/e-library
- 47 -
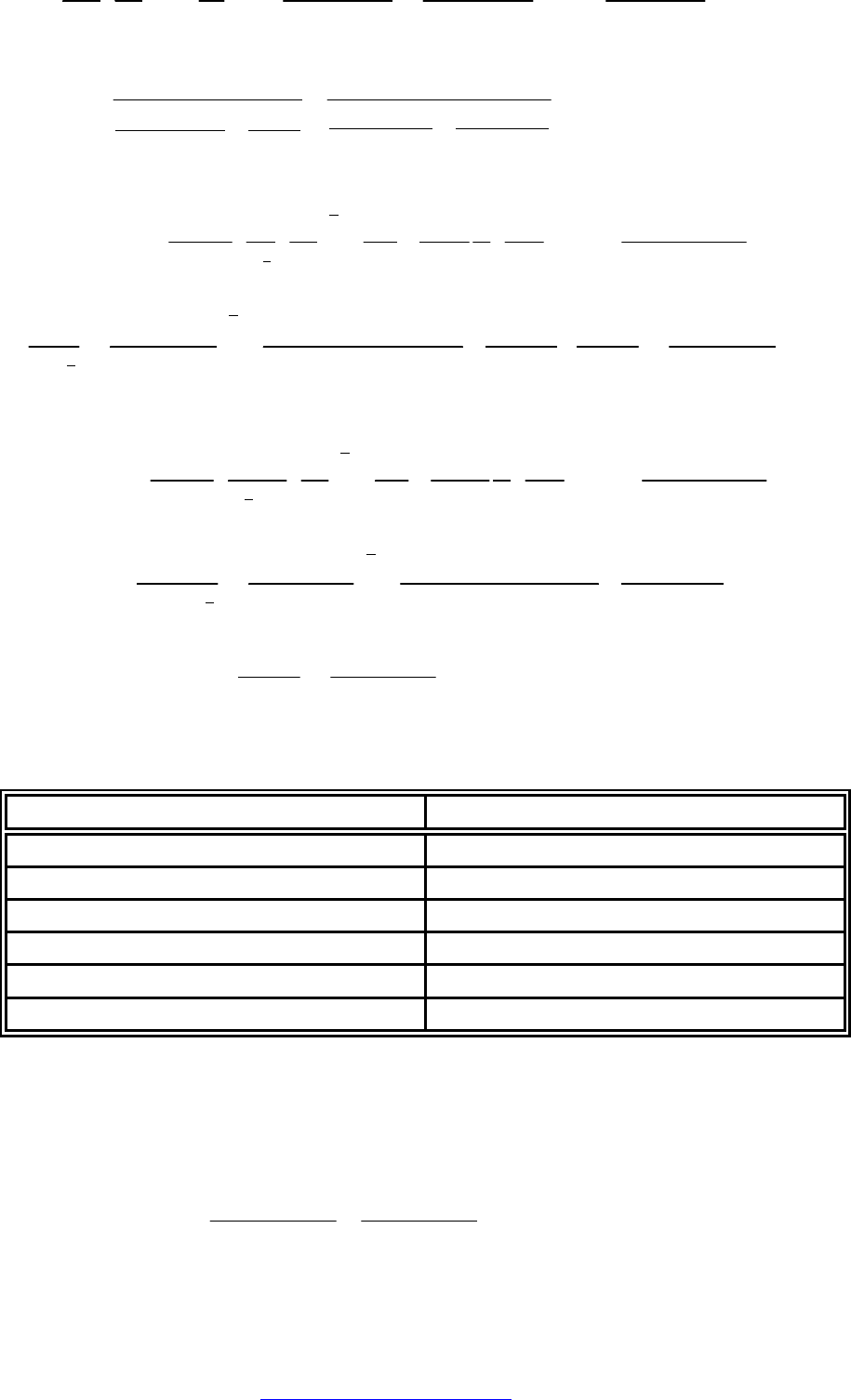
0,3
0,3
0,23
0,23
2 7 4
b b
7 52
S
M ν
P 1,8 10 2,95 10 9,81 10
0,324.
M ν P
3,1 10 3,92 10
3,62 10
Где:
2
1 1
1 2
b
2
1 1
M 3,62 10
кг/моль.
a 1 a 0,6 1 0,6
1,11 10 1,8 10
M
_
M CaCl
Нахождение расчётного значения поверхности теплообмена:
4
0,33
3
НОВ1
1 0,7
К
0b
3
1 1 Q Qδ 1 1 Q 1
F
T t A
λ B 130,4 71,2
F
F
4
0,33
3 3 3 3
3
1 0,7
3
1 4892 10 4892 10 2 10 1 1 4892 10
8764 17,2 0,324 10,90
122
122
= 135,61 м
2
.
4
0,33
3
НОВ2
1 0,7
К
0b
НОВ1
3
НОВ1
1 1 Q Qδ 1 1 Q 1
F
T t A
λ B 130,4 71,2
F
F
3 3
4
3
3
1 0,7
3
1 4892 10 4892 10 2 10 1
8764 17,2
135,61
135,61
3
0,33
2
1 4892 10
143,55
м .
0,324 10, 0
_
9
Проводим итерацию, получая всё более близкое к действительному
значения поверхности теплообмена. В итоге имеем следующие результаты:
F
СТАР
F
НОВ
122 135,61
135,61 143,55
143,55 148,09
148,09 150,66
150,66 152,11
152,11 152,93
В итоге получаем значение поверхности теплообмена:
F = 152,9 м
2
.
Выбор выпарного аппарата:
F = 160 м
2
; d = 38×2 мм; H = 4 м.
Коэффициент запаса:
РАБ РАСЧ
РАСЧ
F F
160 152,9
ψ 0,0464 4,64 %.
F 152,9
_
Расход греющего пара:
www.mitht.ru/e-library
- 48 -
3
3 3
Г
Г
К
Q 4892 10
D 2,253
кг/с.
h h 2719 10 548 1
_
0
Расчёт узла создания вакуума.
Расход конденсируемого пара:
W = 2,146 кг/с.
Температура конденсируемого пара:
θ' = θ – δ
Г
= 41,1 – 1,5 = 39,6 °C.
Рабочее давление в конденсаторе:
при θ' = 39,6 °C P
К
= 7,3 кПа.
Энтальпия конденсируемого пара:
при P
К
= 7,3 кПа h
П
= 2575 кДж/кг.
Температура конденсата на выходе из конденсатора:
t"
В
= θ' – 2,6 = 39,6 – 2,6 = 37 °C.
Расход охлаждающей воды:
3 3
3
П В В
В
В В В
h C t
2575 10 4,19 10 37
G W 2,146 61,97
кг/с.
4,19 10 37 17
C t t
_
Вязкость воды:
при t"
В
= 37 °C μ
В
= 6,925 × 10
–4
Па×с.
Плотность воды:
при t"
В
= 37 °C ρ
В
= 993 кг/м
3
.
Скорость движения воды в трубе:
принимаем w
В
= 0,5 м/с.
Диаметр трубы:
В
В В
W G
2,146 61,97
d 0,406
м 0,4 м.
0,785w ρ 0,78
_
5 0,5 9
_
93
Режим движения воды в трубе:
5
В В В
4
В В
w d w dρ
0,5 0,4 993
Re 2,87 10 .
ν μ
6,925 10
Коэффициент гидравлического сопротивления:
СОПР
0,237 0,237
5
0,221 0,221
λ 0,0032 0,0032 0,014.
Re
2,87 10
Коэффициент местного сопротивления на входе в трубу:
ε
ВХ
= 0,5.
Коэффициент местного сопротивления на выходе из трубы:
ε
ВЫХ
= 1.
Потерянный напор:
2
В
ПОТЕР СОПР
w
H 4 0,5
h λ ξ 0,014 0,5 1 0,042
м.
d 2g 0,4 2 9,80665
_
Высота барометрической трубы:
34
К
ТР
ПОТЕР
B P
9,81 10 7,3 10
H h ΔH 0,042 0,5 9,78
м.
ρg 993 9,80665
_
Принимаем H
ТР
= 10 м.
Объём барометрического ящика:
www.mitht.ru/e-library

- 49 -
2 2
3
ЯЩ ТР
πd 3,14 0,4
V H 10 1,257
м .
4 4
_
Температура отсасываемой паро-воздушной смеси:
t
ПГ
= t
П
= t
Г
= t'
В
+ 4 + 0,1(t"
В
– t'
В
) = 17 + 4 + 0,1 × (37 – 17) = 23 °C.
Парциальное давление водяного пара:
при t
П
= 23 °C P
П
= 2817 Па.
Парциальное давление воздуха:
P
Г
= P
К
– P
П
= 7,3 ×10
3
– 2817 = 4483 Па.
Массовый расход отсасываемого воздуха:
3 3
Г В
G 0,025 W G 10W 10 0,025 2,146 61,97 10 2,146 10
= 0,023 кг/с.
Объёмный расход воздуха:
3
3
Г Г
Г ПГ Г
Г
8,314472 23 273,15
R T
V V G 0,023 0,0126
м /с.
P 4,5 10
_
Теоретическая мощность на валу двигателя вакуум-насоса:
3
3
n 1
1,2 1
n 5
1,2
ВЫХ
Т ПГК
К
P
n 1,2 1,03 10
N P V 7,3 10 0,0126
n 1 P 1,2 1 7,3 10
= 858 Вт ≈ 0,86 кВт.
www.mitht.ru/e-library

- 50 -
Приложение.
Таблица №1.
Теплофизические свойства изоляционных и строительных материалов
(при 20 °C).
Материал ρ, кг/м
3
C
P
,
Дж/(кг×К)
λ, Вт/(м×К) a × 10
6
, м
2
/с
асбест 383 816 0,113 0,036
асфальт 2120 – 0,698 –
бакелит 1270 – 0,233 –
бетон (сухой) 500 837 0,128 0,049
глина (48,7 % вл.) 1545 880 1,26 0,101
гранит 2750 – 3,0 –
дерево:
дуб 609 – 801 2390 0,17 – 0,21
0,0111–0,0121
сосна, пихта, ель 416 – 421 2720 0,15 0,0124
листовое 200 – 0,047 –
целлотекс 400 – 0,055 –
земля:
глинистая (28 % вл.)
1500 – 1,51 –
диатомовая 466 879 0,126 0,031
песчаная (8 % вл.) 1500 – 1,05 –
капок 25 – 0,035 –
картон – – 0,14 – 0,35 –
кирпич:
карборундовый (50 SiC)
2200 – 5,82 –
магнезитовый (50 MgO)
2000 – 2,68 –
обычный 1800 840 0,38 – 0,52 0,028 – 0,034
силикатный (95 SiO
2
)
1900 – 1,07 –
строительный 1700 837 0,658 0,046
цирконный (62 ZrO
2
)
3600 – 2,44 –
кора сосновая 342 – 0,080 –
лёд (0 °C) 913 1830 2,22 0,124
линолеум 535 – 0,081 –
опилки древесные 215 – 0,071 –
песок:
влажный 1640 – 1,13 –
сухой – – 0,582 –
плексиглас 1180 – 0,195 –
полистирол 1050 – 0,157 –
www.mitht.ru/e-library
