Alciatore D.G., Histand M.B. Introduction to Mechatronics and Measurement Systems

Подождите немного. Документ загружается.

Confirming Pages

9.3 Stress and Strain Measurement 391

presented in Threaded Design Example C.3. The serial communication between the PICs is

also described there.

' Define I/O pin names and constants

enc_start Var PORTA.0 ' signal line used to start encoder data transmission

enc_serial Var PORTA.1 ' serial line used to transmit encoder data

enc_sel Var PORTA.2 ' encoder data byte select (0:high 1:low)

enc_oe Var PORTA.3 ' encoder output enable latch signal (active low)

enc_mode Con 2 ' 9600 baud mode for serial communication

' Main loop

start:

' Wait for the start signal from the master PIC to go high

While (enc_start == 0) : Wend

' Enable the encoder output (latch the counter values)

Low enc_oe

' Send out the high byte of the counter

SEROUT enc_serial, enc_mode, [PORTB]

' Wait for the start signal from the master PIC to go low

While (enc_start == 1) : Wend

' Send out the low byte of the counter

High enc_sel

SEROUT enc_serial, enc_mode, [PORTB]

' Disable the encoder output

High enc_oe

Low enc_sel

goto start ' wait for next request

9.3 STRESS AND STRAIN MEASUREMENT

Measurement of stress in a mechanical component is important when assessing

whether or not the component is subjected to safe load levels. Stress and strain mea-

surements can also be used to indirectly measure other physical quantities such as

force (by measuring strain of a flexural element), pressure (by measuring strain in

a flexible diaphragm), and temperature (by measuring thermal expansion of a mate-

rial). The most common transducer used to measure strain is the electrical resistance

strain gage. As we will see, stress values can be determined from strain measure-

ments using principles of solid mechanics.

Basic stress and strain relations and planar stress analysis techniques are pre-

sented in Appendix C for your review if necessary.

alc80237_ch09_375-430.indd 391alc80237_ch09_375-430.indd 391 10/01/11 10:09 PM10/01/11 10:09 PM

Confirming Pages

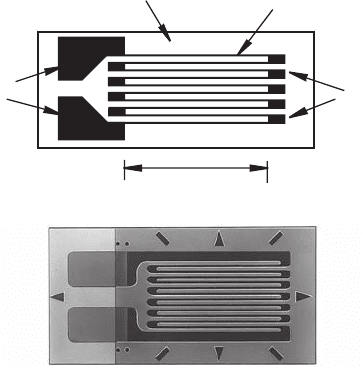
Figure 9.19 Metal foil strain gage construction.

foil grid lines

solder

tabs

backing

end

loops

active length

(a) schematic

(b) actual (Courtesy of Measurements

Group Inc., Raleigh, NC)

392 CHAPTER 9 Sensors

9.3.1 Electrical Resistance Strain Gage

The most common transducer for experimentally measuring strain in a mechanical

component is the bonded metal foil strain gage illustrated in Figure 9.19 . It consists

of a thin foil of metal, usually constantan, deposited as a grid pattern onto a thin plas-

tic backing material, usually polyimide. The foil pattern is terminated at both ends

with large metallic pads that allow leadwires to be easily attached with solder. The

entire gage is usually very small, typically 5 to 15 mm long.

To measure strain on the surface of a machine component or structural mem-

ber, the gage is adhesively bonded directly to the component, usually with epoxy

or cyanoacrylate. The backing makes the foil gage easy to handle and provides a

good bonding surface that also electrically insulates the metal foil from the com-

ponent. Leadwires are then soldered to the solder tabs on the gage. When the

component is loaded, the metal foil deforms, and the resistance changes in a pre-

dictable way (see below). If this resistance change is measured accurately, the

strain on the surface of the component can be determined. Strain measurements

allow us to determine the state of stress on the surface of the component, where

stresses typically have their highest values. Knowing stresses at critical locations

on a component under load can help a designer validate analytical or numerical

results (e.g., from a finite element analysis) and verify that stress levels remain

below safe limits for the material (e.g., below the yield strength). It is important to

note that, because strain gages are finite in size, a measurement actually reflects

an average of the strain over a small area. Hence, making measurements where

stress gradients are large (e.g., where there is stress concentration) can yield poor

results.

alc80237_ch09_375-430.indd 392alc80237_ch09_375-430.indd 392 10/01/11 10:09 PM10/01/11 10:09 PM

Confirming Pages

Figure 9.20 Strain gage application. (Courtesy of Measurements

Group Inc., Raleigh, NC)

9.3 Stress and Strain Measurement 393

Experimental stress analysis (e.g., with strain gages) and analytical or numerical

stress analysis (e.g., with finite element analysis) are both important to design reli-

able mechanical parts. The two approaches should be considered complements to

each other and not replacements. Finite element analysis involves many assumptions

about material properties, load application, and boundary conditions that may not

accurately model the actual component when it is manufactured and loaded. Strain

gage measurements may also have some inaccuracies due to imperfect bonding and

alignment on the component surface and due to uncompensated temperature effects.

Also, only specific locations can be checked with strain gages because space and

access on the component can be limiting factors.

Effects that are easily measured with strain gages but difficult to model with

finite element analysis include stresses resulting from mechanical assembly of com-

ponents and complex loading and boundary conditions. These and other effects are

often difficult to predict and model accurately with analytical and numerical methods.

Experimental stress applications usually involve mounting a large number of

strain gages on a mechanical component, as illustrated in Figure 9.20 , before it is

loaded. Experimental strain values are usually acquired through an automated data

acquisition system. The strain data can be converted to stresses in the object under

different loading conditions, and the stresses can be compared to analytical and

numerical finite element analysis results.

To understand how a strain gage is used to measure strain, we first look at how

the resistance of the foil changes when deformed. The metal foil grid lines in the

active portion of the gage (see Figure 9.19a) can be approximated by a single rectan-

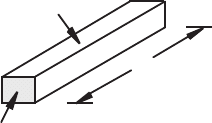
gular conductor as illustrated in Figure 9.21 , whose total resistance is given by

ρL

------

(9.2)

alc80237_ch09_375-430.indd 393alc80237_ch09_375-430.indd 393 10/01/11 10:09 PM10/01/11 10:09 PM

Confirming Pages

Figure 9.21 Rectangular conductor.

394 CHAPTER 9 Sensors

where ␳ is the foil metal resistivity, L is the total length of the grid lines, and A is the

grid line cross-sectional area. The gage end loops and solder tabs have negligible

effects on the gage resistance because they typically have a much larger cross section

than the foil lines.

To see how the resistance changes under deformation, we need to take the dif-

ferential of Equation 9.2. If we first take the natural logarithm of both sides,

Rln

ln Lln Aln–+=

(9.3)

taking the differential yields the following expression for the change in resistance

given material property and geometry changes in the conductor:

dRR⁄ dρρ⁄ dLL⁄ dAA⁄–+=

(9.4)

As we would expect, the signs in this equation imply that the resistance of the

conductor increases (d R > 0) with increased resistivity and increased length and

decreases with increased cross-sectional area. Because the cross-sectional area of

the conductor is

Awh=

(9.5)

the area differential term is

------ -

w dh⋅ h dw⋅+

wh⋅

------------------------------------

------

-------

+==

(9.6)

From the definition of Poisson’s ratio (see Appendix C),

------

–=

(9.7)

and

-------

------

–=

(9.8)

------ -

2– ν

------

2– νε

axial

(9.9)

where ε

axial

is the axial strain in the conductor (see Appendix C). When the conduc-

tor is elongated (ε

axial

> 0), the cross-sectional area decreases (d A / A < 0), causing the

resistance to increase.

alc80237_ch09_375-430.indd 394alc80237_ch09_375-430.indd 394 10/01/11 10:09 PM10/01/11 10:09 PM

Confirming Pages

9.3 Stress and Strain Measurement 395

Using Equation 9.9 , Equation 9.4 can be expressed as

dRR⁄ε

axial

12ν+()dρρ⁄+=

(9.10)

Dividing through by ε

axial

gives

dRR⁄

axial

-------------- 12ν+

dρρ⁄

axial

-------------

(9.11)

The first two terms on the right-hand side, 1 and 2 ␯ , represent the change in resis-

tance due to increased length and decreased area. The last term (d ␳ / ␳ )/(ε

axial

) rep-

resents the piezoresistive effect in the material, which explains how the resistivity of

the material changes with strain. All three terms are approximately constant over the

operating range of typical strain gage metal foils.

Commercially available strain gage specifications usually report a constant gage

factor F to represent the right-hand side of Equation 9.11. This factor represents the

material characteristics of the gage that relate the gage’s change in resistance to strain:

ΔRR⁄

axial

---------------

(9.12)

Thus, when a gage of known resistance R and gage factor F is bonded to the surface

of a component and the component is then loaded, we can determine the strain in the

gage ε

axial

simply by measuring the change in resistance of the gage Δ R:

axial

ΔRR⁄

---------------

(9.13)

This gage strain is the strain on the surface of the loaded component in the direction

of the gage’s long dimension.

For the bonded metal foil strain gage, the gage factor F is usually close to 2, and

the gage resistance R is close to 120 Ω. Strain gage suppliers also report a trans-

verse sensitivity for the gage, which is a measure of the resistance changes in the

end loops and grid lines due to strain in the transverse direction. The transverse

sensitivity for a bonded metal foil gage is usually close to 1%. This number predicts

the gage’s sensitivity to transverse strains: those perpendicular to the measuring axis

of the gage. A gage experiencing 50 ␮ ε (50 ⫻ 10

⫺ 6

, read as “50 microstrain”) in the

axial direction and 100 ␮ε in the transverse direction with a transverse sensitivity of

1% will sense 51 ␮ ε (50 ⫹ 1% of 100), not 50 ␮ ε.

If a 120 Ω strain gage with gage factor 2.0 is used to measure a strain of 100 ␮ ε (100 ⫻ 10

⫺ 6

how much does the resistance of the gage change from the unloaded state to the loaded

state?

Equation 9.12 tells us that

ΔRRFε⋅⋅=

so the change in resistance would be

ΔR 120 Ω

()

2.0

()

0.000100

()

0.024 Ω==

Strain Gage Resistance Changes

EXAMPLE 9.1

alc80237_ch09_375-430.indd 395alc80237_ch09_375-430.indd 395 10/01/11 10:09 PM10/01/11 10:09 PM

Confirming Pages

Figure 9.22 Static balanced bridge circuit.

Hi Z

: strain gage

: potentiomete

396 CHAPTER 9 Sensors

9.3.2 Measuring Resistance Changes

with a Wheatstone Bridge

To use strain gages to accurately measure strains experimentally, we need to be able

to accurately measure small changes in resistance. The most common circuit used to

measure small changes in resistance is the Wheatstone bridge, which consists of a

four-resistor network excited by a DC voltage. A Wheatstone bridge is better than

a simple voltage divider because it can be easily balanced to establish an accurate

zero position, it allows temperature compensation, and it can provide better sensitiv-

ity and accuracy. There are two different modes of operation of a Wheatstone bridge

circuit: the static balanced mode and the dynamic unbalanced mode. For the static

balanced mode, illustrated in Figure 9.22 , R

and R

are precision resistors, R

is a

precision potentiometer (variable resistor) with an accurate scale for displaying the

resistance value, and R

is the strain gage resistance for which the change is to be

measured. To balance the bridge, the variable resistor is adjusted until the voltage

between nodes A and B is 0. In the balanced state, the voltages at A and B must be

equal so

= i

(9.14)

Also, because the high-input impedance voltmeter between A and B is assumed to

draw no current,

-----------------

(9.15)

and

-----------------

(9.16)

■ CLASS DISCUSSION ITEM 9.8

Piezoresistive Effect in Strain Gages

For a typical metal foil strain gage with a gage factor of 2.0, how large is the piezo-

resistive effect in comparison to the effects of change in area and change in length?

alc80237_ch09_375-430.indd 396alc80237_ch09_375-430.indd 396 10/01/11 10:09 PM10/01/11 10:09 PM

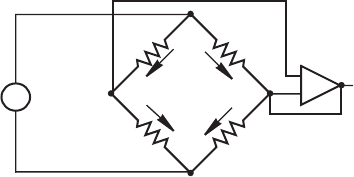
Confirming Pages

Figure 9.23 Dynamic unbalanced bridge circuit.

differential

buffer

amplifier

−

9.3 Stress and Strain Measurement 397

where V

is the DC voltage applied to the bridge called the excitation voltage. Sub-

stituting these expressions into Equation 9.14 and rearranging gives

-----

(9.17)

If we know R

and R

accurately and we note the value for R

on the precision poten-

tiometer scale, we can accurately calculate the unknown resistance R

----------- -

(9.18)

Note that this result is independent of the excitation voltage, V

(see Class Discus-

sion Item 9.9).

The static balanced mode of operation can be used to measure a gage’s resis-

tance under fixed load, but usually balancing is done only as a preliminary step

to measuring changes in gage resistance. In dynamic deflection operation (see

Figure 9.23 ), again with R

representing a strain gage and R

representing a poten-

tiometer, the bridge is first balanced, before loads are applied, by adjusting R

until

there is no output voltage. Then changes in the strain gage resistance R

that occur

under time-varying load can be determined from changes in the output voltage.

The output voltage can be expressed in terms of the resistor currents as

out

– i

+==

(9.19)

and the excitation voltage can be related to the currents:

+()i

+()==

(9.20)

Solving for i

and i

in terms of V

in Equation 9.20 and substituting these into the

first expression in Equation 9.19 gives

out

-----------------

-----------------–

⎝⎠

⎛⎞

(9.21)

When the bridge is balanced, V

out

is 0 and R

has a known value. When R

changes value, as the strain gage is loaded, Equation 9.21 can be used to relate this

voltage change Δ V

out

to the change in resistance Δ R

. To find this relation, we can

alc80237_ch09_375-430.indd 397alc80237_ch09_375-430.indd 397 10/01/11 10:09 PM10/01/11 10:09 PM

Confirming Pages

398 CHAPTER 9 Sensors

replace R

by its new resistance R

⫹ Δ R

and V

out

by the output deflection voltage

Δ V

out

. Then Equation 9.21 gives

ΔV

out

------------

ΔR

----------------------------------

-----------------–=

(9.22)

Rearranging this equation gives us the desired relation between the change in

resistance and the measured output voltage:

ΔR

---------

-----

ΔV

out

------------

-----------------

⎝⎠

⎛⎞

ΔV

out

------------–

-----------------

–

⎝⎠

⎛⎞

---------------------------------------------------- 1–=

(9.23)

By measuring the change in the output voltage Δ V

out

, we can determine the gage

resistance change Δ R

from Equation 9.23 and can compute the gage strain from

Equation 9.13. The differential buffer amplifier shown in Figure 9.23 provides high

input impedance (i.e., it does not load the bridge) and high gain for the small change

in voltage due to the small change in resistance.

■ CLASS DISCUSSION ITEM 9.9

Wheatstone Bridge Excitation Voltage

What undesirable effects can the magnitude of the excitation voltage have on the

resistance change measurements made with a Wheatstone bridge?

Figure 9.24 illustrates the effects of leadwires when using a strain gage located

far from the bridge circuit. Figure 9.24a illustrates a two-wire connection from a

strain gage to a bridge circuit. With this configuration, each of the leadwire resis-

tances R

⬘

adds to the resistance of the strain gage branch of the bridge. The problem

with this is that, if the leadwire temperature changes, it causes changes in the resis-

tance of the bridge branch. This effect can be substantial if the leadwires are long

and extend through environments where the temperature changes. Figure 9.24b

illustrates a three-wire connection that solves this problem. With this configura-

tion, equal leadwire resistances are added to adjacent branches in the bridge so the

effects of changes in the leadwire resistances offset each other. The third leadwire

is connected to the high-input impedance voltage measuring circuit, and its resis-

tance has a negligible effect because it carries negligible current. The three wires

are usually in the form of a small ribbon cable to ensure they experience the same

temperature changes and to minimize electromagnetic interference due to inductive

coupling.

In addition to temperature effects in leadwires, temperature changes in the

strain gage can cause significant changes in resistance, which would lead to erro-

neous measurements. A convenient method for eliminating this effect is to use

alc80237_ch09_375-430.indd 398alc80237_ch09_375-430.indd 398 10/01/11 10:09 PM10/01/11 10:09 PM

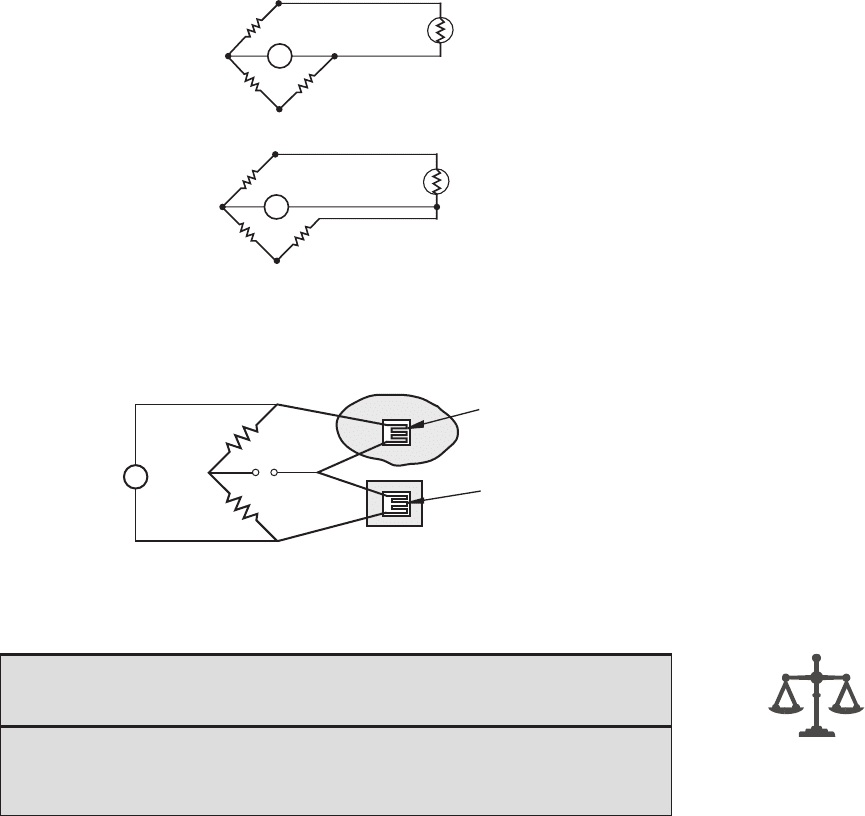
Confirming Pages

Figure 9.24 Leadwire effects in 1/4 bridge circuits.

(a) 2-wire connection

(b) 3-wire connection

Figure 9.25 Temperature compensation with a dummy gage in a half bridge circuit.

part to be loaded

unstressed material of same

composition and at same temperature

dummy gage

active gage

9.3 Stress and Strain Measurement 399

the circuit (called a half bridge) illustrated in Figure 9.25 , where two of the four

bridge legs contain strain gages. The gage in the top branch is the active gage used

to measure surface strains on a component to be loaded. The second “dummy”

gage is mounted to an unloaded sample of material identical in composition to

the component. If this sample is kept at the same temperature as the component

by keeping it in close proximity, the resistance changes in the two gages due to

temperature cancel because they are in adjacent branches of the bridge circuit.

Therefore, the bridge generates an unbalanced voltage only in response to strain

in the active gage.

■ CLASS DISCUSSION ITEM 9.10

Bridge Resistances in Three-Wire Bridges

What must be true about the bridge resistance R

for the three-wire configuration

shown in Figure 9.24b to result in a balanced bridge ( V

⫽ 0) in the no-strain condi-

tion? (Hint: Use Equation 9.21 and assume R

⫽ R

alc80237_ch09_375-430.indd 399alc80237_ch09_375-430.indd 399 10/01/11 10:09 PM10/01/11 10:09 PM

Confirming Pages

Figure 9.26 Bar under uniaxial stress.

strain

gage (ε

)

400 CHAPTER 9 Sensors

9.3.3 Measuring Different States of Stress

with Strain Gages

Mechanical components may have complex shapes and are often subjected to com-

plex loading conditions. In these cases, it is difficult to predict the orientation of

principal stresses at arbitrary points on the component. However, with some geom-

etries and loading conditions, the principal axes are known, and measuring the state

of stress is easier.

If a component is loaded uniaxially (i.e., loaded in only one direction in tension

or compression), the state of stress in the component can be determined with a single

gage mounted in the direction of the load. Figure 9.26 illustrates a bar in tension and

the associated state of stress. By measuring the strain ε

, the stress is obtained using

Hooke’s law (see Appendix C):

Eε

(9.24)

where the axial stress in the ␴

is given by

---

(9.25)

where A is the bar’s cross-sectional area. Therefore, the force P applied to the bar

can be determined from the strain gage measurement:

PAEε

(9.26)

If a component is known to be loaded biaxially (i.e., loaded in two orthogonal

directions in tension or compression), the state of stress in the component can be

determined with two gages aligned with the stress directions. Figure 9.27 illustrates

a pressurized tank and the associated state of stress. By measuring the strains ε

and

, the stresses in the tank shell can be determined from Hooke’s law generalized to

two dimensions:

----- ν

-----

–=

(9.27)

----- ν

-----

–=

(9.28)

alc80237_ch09_375-430.indd 400alc80237_ch09_375-430.indd 400 10/01/11 10:09 PM10/01/11 10:09 PM