Акимов В.А., Лапин В.Л., Попов В.М. и др. Надежность технических систем и техногенный риск. Учебное пособие
Подождите немного. Документ загружается.


4.3.2. Ñëó÷àéíàÿ âåëè÷èíà
Ñëó÷àéíàÿ âåëè÷èíà — âåëè÷èíà, êîòîðàÿ â ðåçóëüòàòå îïûòà ìîæåò ïðè
-
íèìàòü òî èëè èíîå çíà÷åíèå, ïðè÷åì íåèçâåñòíî çàðàíåå êàêîå èìåííî.
Ñëó÷àéíàÿ âåëè÷èíà ìîæåò áûòü äèñêðåòíîé (÷èñëî îòêàçîâ çà âðåìÿ t, ÷èñ
-
ëî îòêàçàâøèõ ýëåìåíòîâ ïðè íàðàáîòêå çàäàííîãî îáúåìà è ò. ä.), ëèáî íå
-
ïðåðûâíîé (âðåìÿ íàðàáîòêè ýëåìåíòà äî îòêàçà, âðåìÿ âîññòàíîâëåíèÿ ðà
-
áîòîñïîñîáíîñòè).
Çàêîí ðàñïðåäåëåíèÿ ñëó÷àéíîé âåëè÷èíû — ñîîòíîøåíèå, óñòàíàâëèâàþ
-
ùåå ñâÿçü ìåæäó çíà÷åíèÿìè ñëó÷àéíîé âåëè÷èíû è èõ âåðîÿòíîñòÿìè.
Îí ìîæåò áûòü ïðåäñòàâëåí ôîðìóëîé, òàáëèöåé, ìíîãîóãîëüíèêîì ðàñïðå
-
äåëåíèé.
Äëÿ õàðàêòåðèñòèêè ñëó÷àéíîé âåëè÷èíû (íåïðåðûâíîé è äèñêðåòíîé)
èñïîëüçóåòñÿ âåðîÿòíîñòü òîãî, ÷òî ñëó÷àéíàÿ âåëè÷èíà X ìåíüøå íåêîòî
-
ðîé òåêóùåé ïåðåìåíîé x.
Ôóíêöèÿ ðàñïðåäåëåíèÿ ñëó÷àéíîé âåëè÷èíû X (èíòåãðàëüíûé çàêîí ðàñ-
ïðåäåëåíèÿ) — ôóíêöèÿ âèäà F(x)=p (X < x).
Ïëîòíîñòü ðàñïðåäåëåíèÿ íåïðåðûâíîé ñëó÷àéíîé âåëè÷èíû X (äèôôåðåí-
öèàëüíûé çàêîí ðàñïðåäåëåíèÿ) — ïðîèçâîäíàÿ îò ôóíêöèè ðàñïðåäåëåíèÿ:
fx
d
dx
Fx() ();= fxdx() ;
–
=
∞
∞
∫
1 fxdx FX
X
() ( )
–
=
∞
∫
.
(4.3.1)
 òåîðèè íàäåæíîñòè çà ñëó÷àéíóþ âåëè÷èíó îáû÷íî ïðèíèìàþò âðåìÿ
ðàáîòû èçäåëèÿ (âðåìÿ äî âîçíèêíîâåíèÿ îòêàçà).  ýòîì ñëó÷àå ôóíêöèÿ
ïëîòíîñòè ðàñïðåäåëåíèÿ f(t) áóäåò ñëóæèòü ïîëíîé õàðàêòåðèñòèêîé ðàññå-
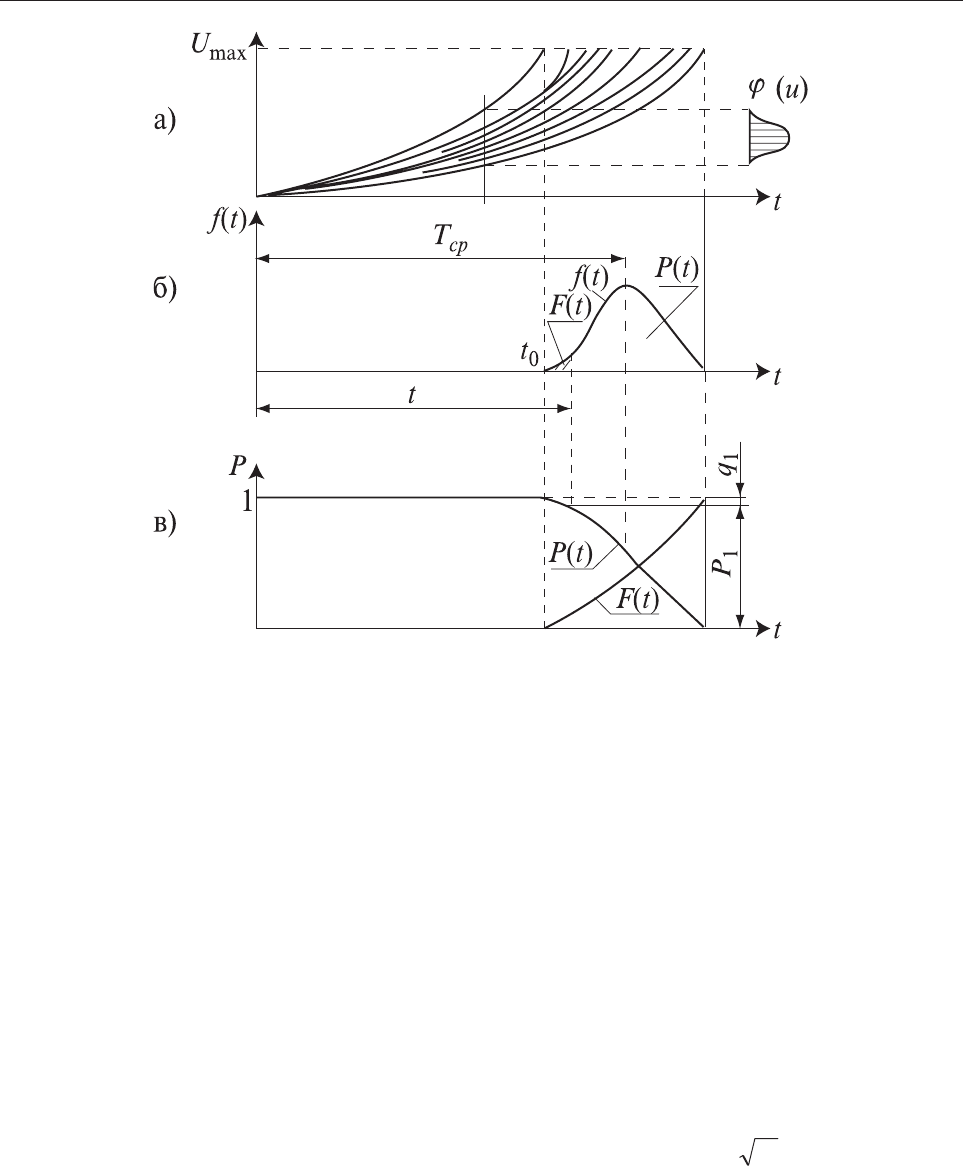
èâàíèÿ ñðîêîâ ñëóæáû ýëåìåíòîâ (ðèñ. 4.3.1). Âèä ýòîé ôóíêöèè çàâèñèò
îò çàêîíîìåðíîñòåé ïðîöåññà ïîòåðè ýëåìåíòîì ðàáîòîñïîñîáíîñòè.
Êðèâàÿ ðàñïðåäåëåíèÿ f(t) — ÷àñòîòà îòêàçîâ — äàåò âîçìîæíîñòü ïîä
-
ñ÷èòàòü ñðåäíèé ñðîê ñëóæáû ýëåìåíòà Ò
ñð
(ìàòåìàòè÷åñêîå îæèäàíèå Ì[t]),
ðàññåèâàíèå (äèñïåðñèþ D) ýòèõ ñðîêîâ ñëóæáû îòíîñèòåëüíî öåíòðà ãðóï
-
ïèðîâàíèÿ è äðóãèå ÷èñëîâûå ïàðàìåòðû ñëó÷àéíîé âåëè÷èíû Ò.
Åñëè âçÿòü íåêîòîðûé ïåðèîä âðåìåíè ðàáîòû ýëåìåíòà t, òî ïëîùàäü
F(t) êðèâîé ðàñïðåäåëåíèÿ f(t) áóäåò õàðàêòåðèçîâàòü âåðîÿòíîñòü îòêàçà
(âûõîäà èç ñòðîÿ) ýëåìåíòà çà ýòîò ïåðèîä âðåìåíè (ðèñ. 4.3.1, á). Ïîýòîìó
ëåâàÿ âåòâü êðèâîé ðàñïðåäåëåíèÿ f(t), îòíîñÿùàÿñÿ ê îáëàñòè ìàëîé âåðî
-
ÿòíîñòè îòêàçîâ, èñïîëüçóåòñÿ îáû÷íî äëÿ õàðàêòåðèñòèêè áåçîòêàçíîñòè
ðàáîòû èçäåëèÿ, à âñÿ êðèâàÿ f(t) è åå ïàðàìåòðû íåîáõîäèìû äëÿ îöåíêè åãî
äîëãîâå÷íîñòè.
Îðäèíàòû èíòåãðàëüíîé ôóíêöèè ðàñïðåäåëåíèÿ F(t ) (ðèñ. 4.3.1, â) õà
-
ðàêòåðèçóþò âåðîÿòíîñòü îòêàçà äåòàëè äî äàííîãî ìîìåíòà âðåìåíè:
Ft ftdt
t
() () .=
∫
0
141
à ËÀÂÀ 4
Âî ìíîãèõ ñëó÷àÿõ íåò íåîáõîäèìîñòè ïîëüçîâàòüñÿ ôóíêöèÿìè F(t) èëè
f(t), äîñòàòî÷íî çíàòü ÷èñëîâûå õàðàêòåðèñòèêè ýòèõ êðèâûõ.
Îñíîâíîé õàðàêòåðèñòèêîé ïîëîæåíèÿ êðèâîé f(t) ÿâëÿåòñÿ ìàòåìàòè÷å-
ñêîå îæèäàíèå Ì[t], êîòîðîå â íàøåì ñëó÷àå ÿâëÿåòñÿ ñðåäíèì ñðîêîì
ñëóæáû Ò
ñð
(íàðàáîòêîé íà îòêàç):
Ttftdt
cp
=
∞
∫
() .
0
Îñíîâíîé õàðàêòåðèñòèêîé ðàññåèâàíèÿ ñëó÷àéíîé âåëè÷èíû ÿâëÿåòñÿ
äèñïåðñèÿ D èëè ñðåäíåå êâàäðàòè÷åñêîå îòêëîíåíèå
σ= D
:
Dt T t f tdt
cp
() ( – ) () .=
∞
∫
2
0
×åì áîëüøå çíà÷åíèå D (èëè ñîîòâåòñòâåííî s), òåì áîëüøå ðàññåèâàíèå
ñðîêîâ ñëóæáû îòíîñèòåëüíî èõ ñðåäíåãî çíà÷åíèÿ Ì[t].
Äëÿ îöåíêè íàäåæíîñòè ðàáîòû ýëåìåíòà, ïðèíèìàÿ çà îñíîâíóþ ñëó
-
÷àéíóþ âåëè÷èíó âðåìÿ äî âîçíèêíîâåíèÿ îòêàçà, ìîæíî îïðåäåëèòü è âå
-
ðîÿòíîñòü áåçîòêàçíîé ðàáîòû P(t) â ïðåäåëàõ çàäàííîãî ïåðèîäà t. Äëÿ ýòî
-
ãî âîñïîëüçóåìñÿ çíà÷åíèåì èíòåãðàëüíîé ôóíêöèè:
142
à ËÀÂÀ 4
Ðèñ. 4.3.1. Êðèâûå ðàñïðåäåëåíèÿ ñëó÷àéíîé âåëè÷èíû ïðè èçíîñîâûõ
(ïîñòåïåííûõ) îòêàçàõ:
à — ðåàëèçàöèÿ ôóíêöèè èçíîñà j(U);
á — ïëîòíîñòü ðàñïðåäåëåíèÿ ñðîêîâ ñëóæáû f(t);
â — èíòåãðàëüíàÿ ôóíêöèÿ ðàñïðåäåëåíèÿ F(t) è âåðîÿòíîñòü áåçîòêàçíîé ðàáîòû P(t)
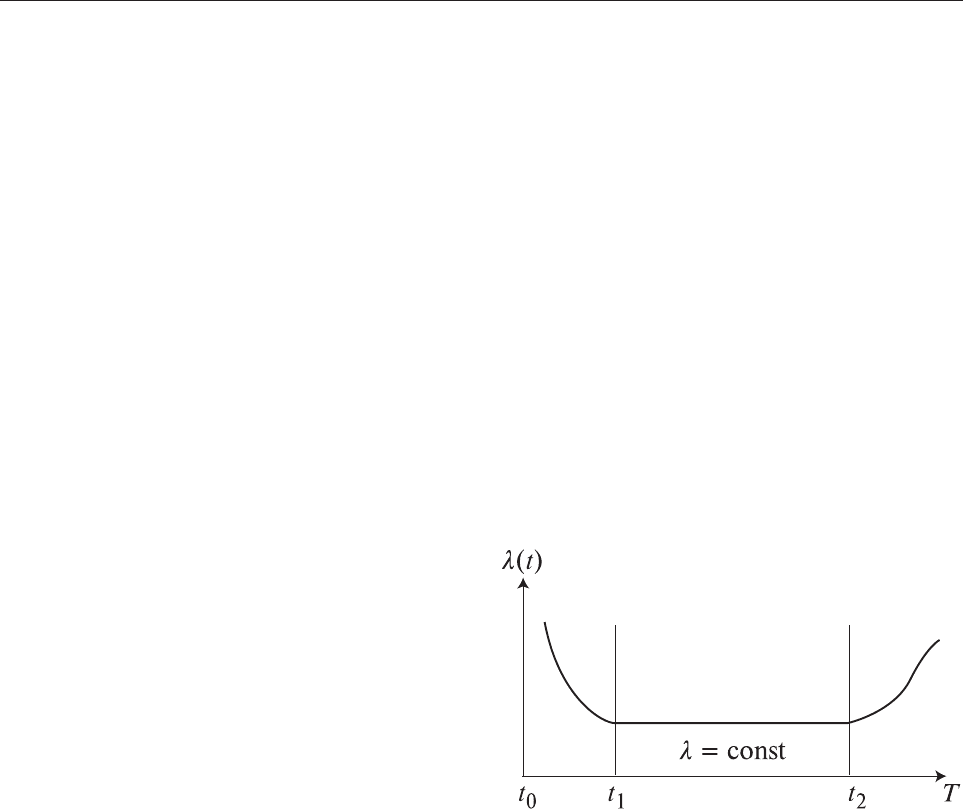
Ft ftdt
t
() () .=
∫
0
Âåðîÿòíîñòü áåçîòêàçíîé ðàáîòû P(t) îòíîñèòñÿ ê ñîáûòèþ, ïðîòèâîïî
-
ëîæíîìó ïîÿâëåíèþ îòêàçà F(t). Ïîýòîìó F(t )+P(t)=1èëèP(t)=1–F(t).
Ñëåäîâàòåëüíî, P(t) îïðåäåëÿåòñÿ (4.2.5).
 ýòîì ñëó÷àå:
—
ôóíêöèÿ ðàñïðåäåëåíèÿ îòêàçà F(t)=P(t < t
çàä
)=Q(t);
—
ïëîòíîñòü ðàñïðåäåëåíèÿ f(t)=dQ(t)/dt;
—
âåðîÿòíîñòü áåçîòêàçíîñòè èçäåëèÿ çà âðåìÿ t: P(t)=1–Q(t).
Èíòåíñèâíîñòü îòêàçîâ (óñëîâíàÿ ïëîòíîñòü âåðîÿòíîñòè îòêàçîâ) —
îòíîøåíèå f(t)êP(t), ñì. (4.2.7):
λ() ()/ ().tftPt=
Òèïè÷íàÿ ôóíêöèÿ èíòåíñèâíîñòè îòêàçîâ èçîáðàæåíà íà ðèñ. 4.3.2.
Ó÷àñòîê óáûâàþùåé èíòåíñèâ
-
íîñòè îòêàçîâ
(–)tt
01
èíîãäà íàçû
-
âàþò ïåðèîäîì ïðèðàáîòêè èëè ïåðè-
îäîì ðàííèõ îòêàçîâ. Ïîÿâëåíèå
îòêàçîâ â ýòîì ïåðèîäå îáû÷íî âû-
çûâàåòñÿ êîíñòðóêòèâíûìè èëè
ïðîèçâîäñòâåííûìè äåôåêòàìè.
Ó÷àñòîê ïîñòîÿííîé èíòåíñèâ-
íîñòè îòêàçîâ
(–)tt
12
íàçûâàþò ïå-
ðèîäîì íîðìàëüíîé ýêñïëóàòàöèè.
Ýòîò ïåðèîä íà÷èíàåòñÿ ñðàçó æå
ïîñëå ïåðèîäà ïðèðàáîòêè è çàêàí-
÷èâàåòñÿ íåïîñðåäñòâåííî ïåðåä ïå-
ðèîäîì èçíîñîâûõ îòêàçîâ.
Ïåðèîä èçíîñîâûõ îòêàçîâ íà÷èíàåòñÿ òîãäà, êîãäà ýëåìåíò (óñòðîéñòâî)
âûðàáîòàë ñâîé ðåñóðñ, âñëåäñòâèå ÷åãî ÷èñëî îòêàçîâ â ýòîì ïåðèîäå íà÷è
-
íàåò âîçðàñòàòü.
Îòêàçû, ïîÿâëÿþùèåñÿ â ïåðèîäå íîðìàëüíîé ýêñïëóàòàöèè, íàçûâàþò
âíåçàïíûìè, òàê êàê îíè ïîÿâëÿþòñÿ â ñëó÷àéíûå ìîìåíòû âðåìåíè, èëè,
äðóãèìè ñëîâàìè, íåïðåäñêàçóåìî.
4.3.3. Îñíîâíûå çàêîíû ðàñïðåäåëåíèÿ, èñïîëüçóåìûå â òåîðèè
íàäåæíîñòè
 òåîðèè íàäåæíîñòè íàèáîëüøåå ðàñïðîñòðàíåíèå ïîëó÷èëè ñëåäóþ
-
ùèå çàêîíû ðàñïðåäåëåíèÿ ñëó÷àéíûõ âåëè÷èí f(t):
—
äëÿ äèñêðåòíûõ ñëó÷àéíûõ âåëè÷èí — áèíîìèíàëüíûé çàêîí; çàêîí
Ïóàññîíà;
143
à ËÀÂÀ 4
Ðèñ. 4.3.2. Òèïè÷íàÿ ôóíêöèÿ
èíòåíñèâíîñòè îòêàçîâ
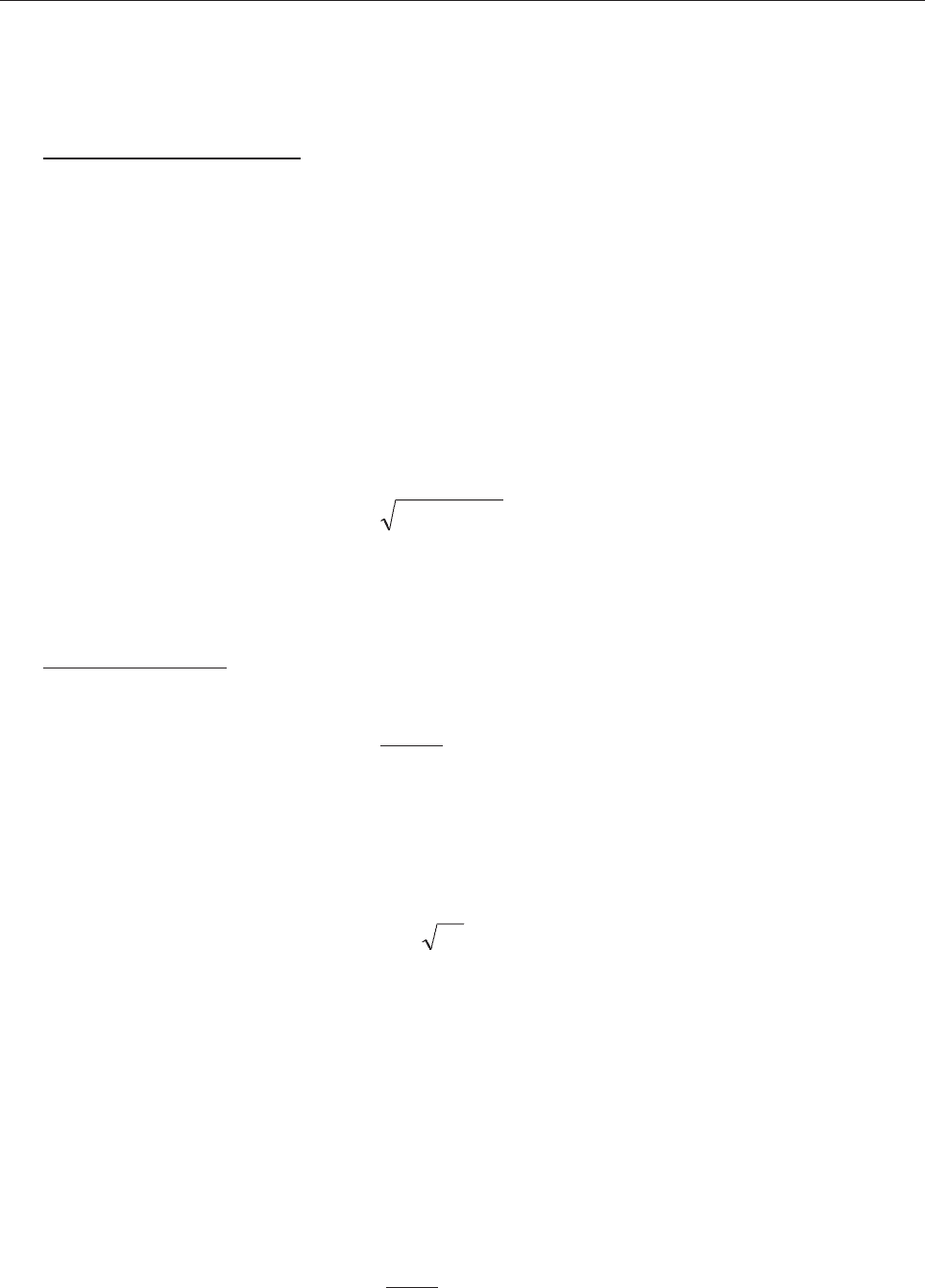
—
äëÿ íåïðåðûâíûõ ñëó÷àéíûõ âåëè÷èí — ýêñïîíåíöèàëüíûé çàêîí;
íîðìàëüíûé çàêîí; ãàììà-ðàñïðåäåëåíèå; çàêîí Âåéáóëëà; c
2
— ðàñ
-
ïðåäåëåíèå; ëîãàðèôìè÷åñêè-íîðìàëüíîå ðàñïðåäåëåíèå.
Áèíîìèíàëüíûé çàêîí
ðàñïðåäåëåíèÿ ÷èñëà n ïîÿâëåíèÿ ñîáûòèÿ A â m
íåçàâèñèìûõ îïûòàõ (èñïûòàíèÿõ). Åñëè âåðîÿòíîñòü ïîÿâëåíèÿ ñîáûòèÿ A
â îäíîì èñïûòàíèè ðàâíà p, âåðîÿòíîñòü íåïîÿâëåíèÿ ñîáûòèÿ A ðàâíà
qp= 1–
; ÷èñëî íåçàâèñèìûõ èñïûòàíèé ðàâíî m, òî âåðîÿòíîñòü ïîÿâëåíèÿ
n ñîáûòèé â èñïûòàíèÿõ áóäåò:
PCp p
m
n
m
n
nmn
= (– )
–
1
, (4.3.2)
ãäå:
C
m
n
—
÷èñëî ñî÷åòàíèé èç m ïî n.
Ñâîéñòâà ðàñïðåäåëåíèÿ ñëåäóþùèå:
1) ÷èñëî ñîáûòèé n — öåëîå ïîëîæèòåëüíîå ÷èñëî;
2) ìàòåìàòè÷åñêîå îæèäàíèå ÷èñëà ñîáûòèé ðàâíî mp;
3) ñðåäíåêâàäðàòè÷åñêîå îòêëîíåíèå ÷èñëà ñîáûòèé:
σ= mp p(– )1
.
Ïðè óâåëè÷åíèè ÷èñëà èñïûòàíèé áèíîìèíàëüíîå ðàñïðåäåëåíèå ïðè-
áëèæàåòñÿ ê íîðìàëüíîìó ñî ñðåäíèì çíà÷åíèåì n/m è äèñïåðñèåé
ppm(– )/ .1
Çàêîí Ïóàññîíà
— ðàñïðåäåëåíèå ÷èñåë ñëó÷àéíîãî ñîáûòèÿ n
i
çà âðåìÿ t.
Âåðîÿòíîñòü âîçíèêíîâåíèÿ ñëó÷àéíîãî ñîáûòèÿ n ðàç çà âðåìÿ t:
P
n
n
n
()
()
!
exp(– )τ
λτ
λτ=
,
(4.3.3)
ãäå:
l
—
èíòåíñèâíîñòü ñëó÷àéíîãî ñîáûòèÿ.
Ñâîéñòâà ðàñïðåäåëåíèÿ ñëåäóþùèå:
1) ìàòåìàòè÷åñêîå îæèäàíèå ÷èñëà ñîáûòèé çà âðåìÿ t ðàâíî lt;
2) ñðåäíåêâàäðàòè÷åñêîå îòêëîíåíèå ÷èñëà ñîáûòèé:
σλτ= .
Õàðàêòåðíûé ïðèçíàê ðàñïðåäåëåíèÿ Ïóàññîíà — ðàâåíñòâî ìàòåìàòè
-
÷åñêîãî îæèäàíèÿ è äèñïåðñèè. Ýòî ñâîéñòâî èñïîëüçóåòñÿ äëÿ ïðîâåðêè
ñòåïåíè ñîîòâåòñòâèÿ èññëåäóåìîãî (îïûòíîãî) ðàñïðåäåëåíèÿ ñ ðàñïðåäå
-
ëåíèåì Ïóàññîíà.
Ðàñïðåäåëåíèå Ïóàññîíà ïîëó÷àåòñÿ èç áèíîìèíàëüíîãî ðàñïðåäåëåíèÿ,
åñëè ÷èñëî èñïûòàíèé m íåîãðàíè÷åííî âîçðàñòàåò, à ìàòåìàòè÷åñêîå îæè
-
äàíèå ÷èñëà ñîáûòèé
a =λτ
îñòàåòñÿ ïîñòîÿííûì.
Òîãäà âåðîÿòíîñòü
P
m
n
áèíîìèíàëüíîãî ðàñïðåäåëåíèÿ ïðè êàæäîì n,
ðàâíîì 0, 1, 2, ..., ñòðåìèòñÿ ê ïðåäåëó:
P
a
n
a
m
n
n
→
()
!
exp(– ).
Çàêîí Ïóàññîíà èñïîëüçóåòñÿ òîãäà, êîãäà íåîáõîäèìî îïðåäåëèòü âåðî
-
ÿòíîñòü òîãî, ÷òî â èçäåëèè çà çàäàííîå âðåìÿ ïðîèçîéäåò îäèí, äâà, òðè
è ò. ä. îòêàçîâ.
144
à ËÀÂÀ 4

Ýêñïîíåíöèàëüíûé (ïîêàçàòåëüíûé) çàêîí ðàñïðåäåëåíèÿ ñëó÷àéíîé âå
-
ëè÷èíû X (ðèñ. 4.3.3, à) çàïèñûâàåòñÿ â îáùåì ñëó÷àå òàê:
Px x() exp(– )=λ
,
ãäå: P(x )—
âåðîÿòíîñòü òîãî, ÷òî ñëó÷àéíàÿ âåëè÷èíà X èìååò çíà÷åíèå
áîëüøå x; çíà÷åíèÿ å
–õ
äàþòñÿ â ïðèëîæåíèè 1.
 ÷àñòíîì ñëó÷àå, êîãäà çà ñëó÷àéíóþ âåëè÷èíó ïðèíèìàåòñÿ âðåìÿ ðà
-
áîòû îáúåêòà t, âåðîÿòíîñòü òîãî, ÷òî èçäåëèå íà ïðîòÿæåíèè âðåìåíè t áó
-
äåò íàõîäèòüñÿ â ðàáîòîñïîñîáíîì ñîñòîÿíèè, ðàâíà åxp(–lt):
Pt t() exp(–=λ)
, (4.3.4)
ãäå:
l
—
èíòåíñèâíîñòü îòêàçîâ îáúåêòà äëÿ ýêñïîíåíöèàëüíîãî ðàñïðå
-
äåëåíèÿ (îíà ïîñòîÿííà), ò. å. l = const.
Âûðàæåíèå (4.3.4) ìîæíî ïîëó÷èòü íåïîñðåäñòâåííî èç (4.3.3), åñëè ÷èñ
-
ëî îòêàçîâ n ïðèíÿòü ðàâíûì 0.
Âåðîÿòíîñòü îòêàçà çà âðåìÿ t èç (4.3.4):
Qt Pt t() – () –exp(– ).==11λ
(4.3.5)
Ïëîòíîñòü âåðîÿòíîñòè îòêàçîâ:
ft()=
¶Q/¶
tt=λ λexp(– )
.
(4.3.6)
Ñðåäíåå âðåìÿ ðàáîòû äî âîçíèêíîâåíèÿ îòêàçà:
T tf t dt P t dt
1
00
1===
∞∞
∫∫
() () /λ
.
(4.3.7)
Äèñïåðñèÿ âðåìåíè ðàáîòû äî âîçíèêíîâåíèÿ îòêàçà:
Dt t T f tdt() ( – ) () /==
∞
∫
1
22
0
1 λ
.
(4.3.8)
Ñðåäíåêâàäðàòè÷åñêîå âðåìÿ ðàáîòû:
σ()tT=
1
. (4.3.9)
Ðàâåíñòâî ñðåäíåêâàäðàòè÷åñêîãî îòêëîíåíèÿ ñðåäíåìó âðåìåíè ðàáî
-
òû — õàðàêòåðíûé ïðèçíàê ýêñïîíåíöèàëüíîãî ðàñïðåäåëåíèÿ.
Ñòàòèñòè÷åñêèå ìàòåðèàëû îá îòêàçàõ ýëåìåíòîâ ñâèäåòåëüñòâóþò î òîì,
÷òî â îñíîâíîì âðåìÿ èõ ðàáîòû ïîä÷èíÿåòñÿ ýêñïîíåíöèàëüíîìó çàêîíó
ðàñïðåäåëåíèÿ. Óñëîâèåì âîçíèêíîâåíèÿ ýêñïîíåíöèàëüíîãî çàêîíà ðàñ
-
ïðåäåëåíèÿ âðåìåíè äî îòêàçà ñëóæèò ïîñòîÿíñòâî èíòåíñèâíîñòè îòêàçîâ,
÷òî õàðàêòåðíî äëÿ âíåçàïíûõ îòêàçîâ íà èíòåðâàëå âðåìåíè, êîãäà ïåðèîä
ïðèðàáîòêè îáúåêòà çàêîí÷èëñÿ, à ïåðèîä èçíîñà è ñòàðåíèÿ åùå íå íà÷àë
-
ñÿ, ò. å. äëÿ íîðìàëüíûõ óñëîâèé ýêñïëóàòàöèè. Ïîñòîÿííîé ñòàíîâèòñÿ èí
-
òåíñèâíîñòü îòêàçîâ ñëîæíûõ îáúåêòîâ, åñëè âûçûâàþòñÿ îíè îòêàçàìè áî
-
ëüøîãî ÷èñëà êîìïëåêòóþùèõ ýëåìåíòîâ.
Âðåìÿ âîçíèêíîâåíèÿ ïåðâè÷íûõ îòêàçîâ ìîæåò áûòü ðàñïîëîæåíî
íà îñè âðåìåíè òàê, ÷òî ñóììàðíûé ïîòîê îòêàçîâ ñëîæíîãî èçäåëèÿ ñòàíî
-
âèòñÿ áëèçêèì ê ïðîñòåéøåìó, ò. å. ñ ïîñòîÿííîé èíòåíñèâíîñòüþ îòêàçîâ.
145
à ËÀÂÀ 4
Ýòèìè îáñòîÿòåëüñòâàìè, à òàêæå òåì, ÷òî ïðåäïîëîæåíèå îá ýêñïîíåí
-
öèàëüíîì ðàñïðåäåëåíèè ñóùåñòâåííî óïðîùàåò ðàñ÷åòû íàäåæíîñòè, îáú
-
ÿñíÿåòñÿ øèðîêîå ïðèìåíåíèå ýêñïîíåíöèàëüíîãî çàêîíà â èíæåíåðíîé
ïðàêòèêå.
Ãàììà-ðàñïðåäåëåíèå
ñëó÷àéíîé âåëè÷èíû (ðèñ. 4.3.3, á). Åñëè îòêàç
óñòðîéñòâà âîçíèêàåò òîãäà, êîãäà ïðîèçîéäåò íå ìåíåå k îòêàçîâ åãî ýëå
-
ìåíòîâ, à îòêàçû ýëåìåíòîâ ïîä÷èíåíû ýêñïîíåíöèàëüíîìó çàêîíó ñ ïàðà
-
ìåòðàìè λ
0
, ïëîòíîñòü âåðîÿòíîñòè îòêàçà óñòðîéñòâà:
146
à ËÀÂÀ 4
f(t) Q(t) P(t) O(t)
f(t) Q(t) P(t) O(t)
f(t) Q(t) P(t) O(t)
f(t) Q(t) P(t) O(t)
f(t) Q(t) P(t) O(t)
f(t) Q(t) P(t) O(t)
à)
á)
â)
ã)
ä)
ñ)
tttt
tttt
tttt
tttt
tttt
tttt
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
k
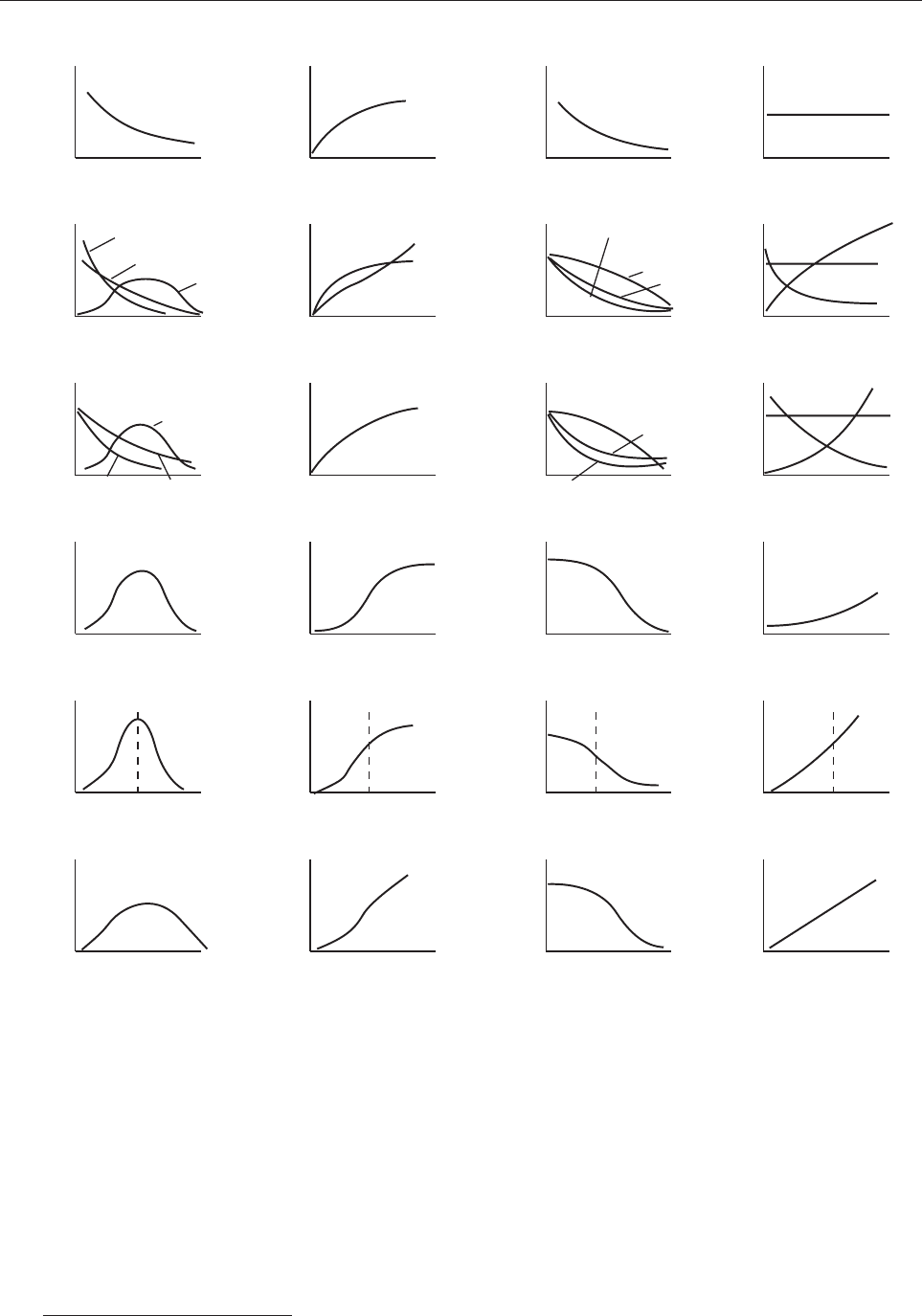
Ðèñ. 4.3.3. Ðàñïðåäåëåíèÿ:
à – ýêñïîíåíöèàëüíîå; á — g-ðàñïðåäåëåíèå; â — Âåéáóëëà;
ã — íîðìàëüíîå; ä — óñå÷åííîå íîðìàëüíîå; å — Ðýëåÿ
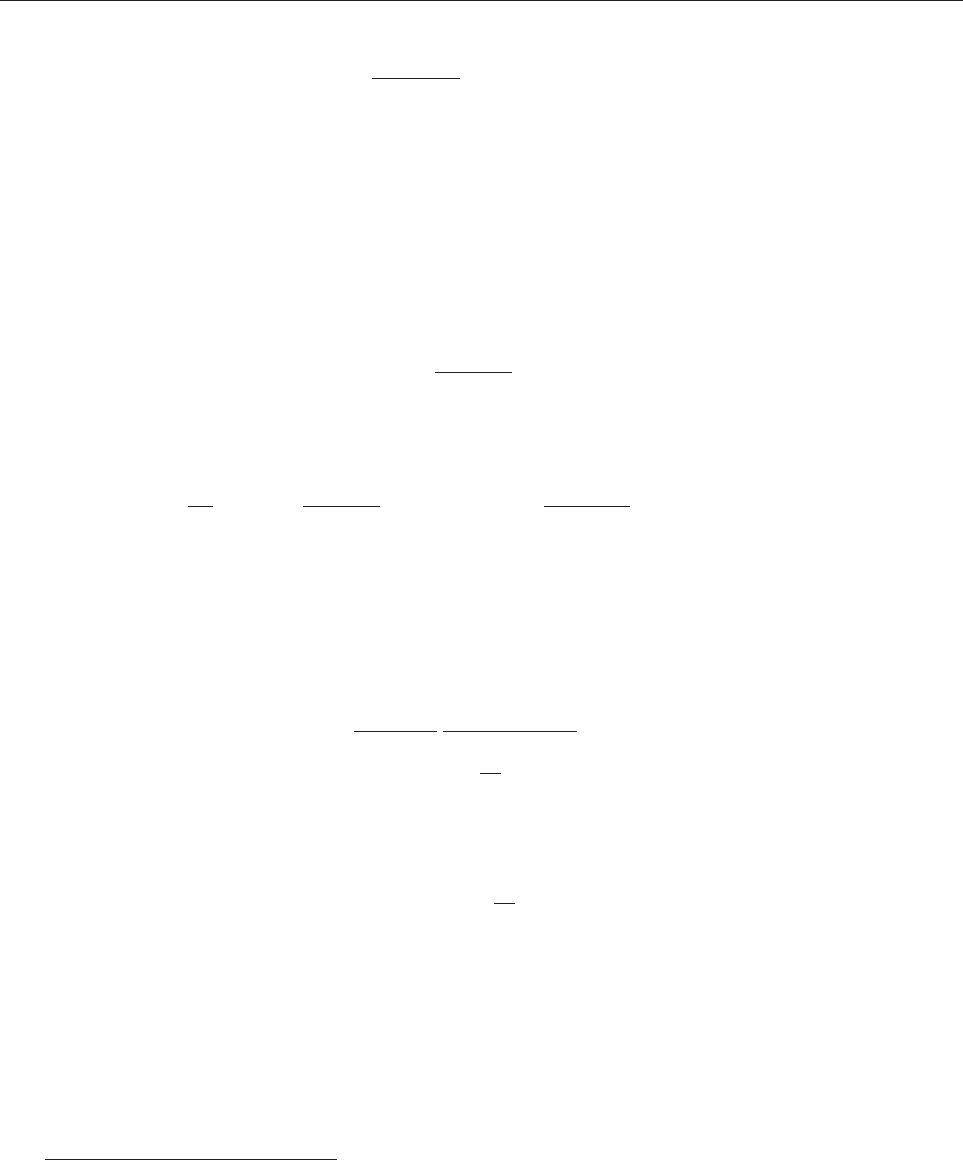
ft
t
k
t
k
k
()
(–)!
exp(– )
–
=
λ
λ
0
1
0
1
,
(4.3.9)
ãäå:
l
0
—
èñõîäíàÿ èíòåíñèâíîñòü îòêàçîâ ýëåìåíòîâ óñòðîéñòâà, îòêàç
êîòîðîãî âûçûâàåòñÿ îòêàçîì k ýëåìåíòîâ.
Ýòîìó ðàñïðåäåëåíèþ ïîä÷èíÿåòñÿ âðåìÿ ðàáîòû ðåçåðâèðîâàííûõ
óñòðîéñòâ. Ðàâåíñòâî (4.3.9) ïîëó÷àåòñÿ èç (4.3.3).
Âåðîÿòíîñòü k è áîëåå îòêàçîâ, ò. å. âåðîÿòíîñòü îòêàçà äàííîãî óñòðîé
-
ñòâà:
Pn k
t
n
t
n
n
k
()–
()
!
exp(– ).
–
≥=
=
∑
1
0
0
1
0
λ
λ
(4.3.10)
Ïëîòíîñòü âåðîÿòíîñòè îòêàçà óñòðîéñòâà çà âðåìÿ t:
()
()
ft
d
dt
t
n
t
t
k
n
n
k
k
k
()
()
!
exp
!
=− −
⎡
⎣
⎢
⎤
⎦
⎥
=
−
=
−
−
∑
1
1
0
0
0
1
0
1
λ
λ
λ
()
exp −λ
0
t
.
(4.3.11)
Ñðåäíåå âðåìÿ ðàáîòû óñòðîéñòâà äî îòêàçà:
TkTk
10 0
==/ λ
. (4.3.12)
Èíòåíñèâíîñòü îòêàçîâ óñòðîéñòâà:
()
()
λ
λ
λ
λ
()
()!
!
t
k
t
i
t
k
i
k
i
=
−
−
=
−
∑
0
0
1
0
1
0
1
1
.
(4.3.13)
Âåðîÿòíîñòü áåçîòêàçíîãî ñîñòîÿíèÿ óñòðîéñòâà:
()
Pt t
i
t
i
io
k
() exp( )
!
.=−
=
−
∑
λλ
00
1
1
(4.3.14)
Ïðè k =1g-ðàñïðåäåëåíèå ñîâïàäàåò ñ ýêñïîíåíöèàëüíûì ðàñïðåäåëå
-
íèåì.
Ïðè óâåëè÷åíèè k g-ðàñïðåäåëåíèå áóäåò ïðèáëèæàòüñÿ ê ñèììåòðè÷íî
-
ìó ðàñïðåäåëåíèþ, à èíòåíñèâíîñòü îòêàçîâ áóäåò èìåòü âñå áîëåå âûðàæåí
-
íûé õàðàêòåð âîçðàñòàþùåé ôóíêöèè âðåìåíè.
Ðàñïðåäåëåíèå Âåéáóëëà
. Äëÿ ñëó÷àÿ, êîãäà ïîòîê îòêàçîâ íå ñòàöèîíàð
-
íûé, ò. å. ïëîòíîñòü ïîòîêà èçìåíÿåòñÿ ñ òå÷åíèåì âðåìåíè, ôóíêöèÿ ðàñ
-
ïðåäåëåíèÿ âðåìåíè äî îòêàçà ïðèîáðåòàåò âèä, ïîêàçàííûé íà ðèñ. 4.3.3, â.
Ïëîòíîñòü âåðîÿòíîñòè îòêàçîâ ýòîãî ðàñïðåäåëåíèÿ:
ft t t() exp( ).=−
−
λα λ
αα1
0
(4.3.15)
Âåðîÿòíîñòü îòñóòñòâèÿ îòêàçà çà âðåìÿ t:
Pt t() exp( ).=−λ
α
0
(4.3.16)
Èíòåíñèâíîñòü îòêàçîâ:
λαλ
α
() .tt=
−
0
1
(4.3.17)
147
à ËÀÂÀ 4

 (4.3.15)—(4.3.17) a è l
0
— ïàðàìåòðû çàêîíà ðàñïðåäåëåíèÿ. Ïàðàìåòð
l
0
îïðåäåëÿåò ìàñøòàá, ïðè åãî èçìåíåíèè êðèâàÿ ðàñïðåäåëåíèÿ ñæèìàåò
-
ñÿ èëè ðàñòÿãèâàåòñÿ. Ïðè a = 1 ôóíêöèÿ ðàñïðåäåëåíèÿ Âåéáóëëà ñîâïàäà
-
åò ñ ýêñïîíåíöèàëüíûì ðàñïðåäåëåíèåì; ïðè
α<1
èíòåíñèâíîñòü îòêàçîâ
áóäåò ìîíîòîííî óáûâàþùåé ôóíêöèåé; ïðè
α>1
— ìîíîòîííî âîçðàñòàþ
-
ùåé. Ýòî îáñòîÿòåëüñòâî äàåò âîçìîæíîñòü ïîäáèðàòü äëÿ îïûòíûõ äàííûõ
íàèáîëåå ïîäõîäÿùèå ïàðàìåòðû a è l
0
, ñ òåì ÷òîáû óðàâíåíèå ôóíêöèè
ðàñïðåäåëåíèÿ íàèëó÷øèì îáðàçîì ñîâïàäàëî ñ îïûòíûìè äàííûìè. Ðàñ
-
ïðåäåëåíèå Âåéáóëëà èìååò ìåñòî äëÿ îòêàçîâ, âîçíèêàþùèõ ïî ïðè÷èíå
óñòàëîñòè òåëà äåòàëè èëè ïîâåðõíîñòíûõ ñëîåâ (ïîäøèïíèêè, çóá÷àòûå ïå
-
ðåäà÷è). Ýòîò ñëó÷àé ñâÿçàí ñ ðàçâèòèåì óñòàëîñòíîé òðåùèíû â çîíå ìåñò
-
íîé êîíöåíòðàöèè íàïðÿæåíèé, òåõíîëîãè÷åñêîãî äåôåêòà èëè íà÷àëüíîãî
ïîâðåæäåíèÿ. Ïåðèîä âðåìåíè äî çàðîæäåíèÿ ìèêðîòðåùèíû õàðàêòåðèçó
-
åòñÿ ïðèçíàêàìè âíåçàïíîãî îòêàçà, à ïðîöåññ ðàçðóøåíèÿ — ïðèçíàêàìè
èçíîñîâîãî îòêàçà.
Ýòîò çàêîí ïðèìåíèì äëÿ îòêàçîâ óñòðîéñòâà, ñîñòîÿùåãî èç ïîñëåäîâà-
òåëüíî ñîåäèíåííûõ äóáëèðîâàííûõ ýëåìåíòîâ è äðóãèõ ïîäîáíûõ ñëó÷àåâ.
Ýòî ðàñïðåäåëåíèå èíîãäà èñïîëüçóåòñÿ äëÿ îïèñàíèÿ íàäåæíîñòè ïîä-
øèïíèêîâ êà÷åíèÿ (a=1,4—1,7).
Ñðåäíÿÿ íàðàáîòêà äî ïåðâîãî îòêàçà îïðåäåëèòñÿ èç ñëåäóþùåãî âûðà-
æåíèÿ:
()
T =
+Γ 11/ α
λ
0
1/α
.
(4.3.18)
Çíà÷åíèÿ
Γ
(ãàììà-ôóíêöèè) òàáóëèðîâàíû (ïðèëîæåíèè 2).
Íîðìàëüíîå ðàñïðåäåëåíèå
(ðèñ. 4.3.3, ã) ñëó÷àéíîé âåëè÷èíû X âîçíèêàåò
âñÿêèé ðàç, êîãäà X çàâèñèò îò áîëüøîãî ÷èñëà îäíîðîäíûõ ïî ñâîåìó âëèÿ-
íèþ ñëó÷àéíûõ ôàêòîðîâ, ïðè÷åì âëèÿíèå êàæäîãî èç ýòèõ ôàêòîðîâ
ïî ñðàâíåíèþ ñ ñîâîêóïíîñòüþ âñåõ îñòàëüíûõ íåçíà÷èòåëüíî. Ýòî óñëîâèå
õàðàêòåðíî äëÿ âðåìåíè âîçíèêíîâåíèÿ îòêàçà, âûçâàííîãî ñòàðåíèåì,
ò. å. ýòîò çàêîí èñïîëüçóåòñÿ äëÿ îöåíêè íàäåæíîñòè èçäåëèé ïðè íàëè÷èè
ïîñòåïåííûõ (èçíîñîâûõ) îòêàçîâ.
Ïëîòíîñòü âåðîÿòíîñòè îòêàçîâ:
()
ft t T() exp /=−−
⎡
⎣
⎢
⎤
⎦
⎥
1
2
2
2
2
σπ
σ
,
(4.3.19)
ãäå: T —
ñðåäíÿÿ íàðàáîòêà äî îòêàçà;
s
—
ñðåäíåå êâàäðàòè÷åñêîå (ñòàíäàðòíîå) îòêëîíåíèå âðåìåíè
áåçîòêàçíîé ðàáîòû.
Âåðîÿòíîñòü îòêàçà âðåìÿ t:
()
Ft ftdt t T
t
() () exp /== −−
⎡
⎣
⎢
⎤
⎦
⎥
−∞ −∞
∫∫
0
2
2
1
2
2
σπ
σ
.
(4.3.20)
148
à ËÀÂÀ 4
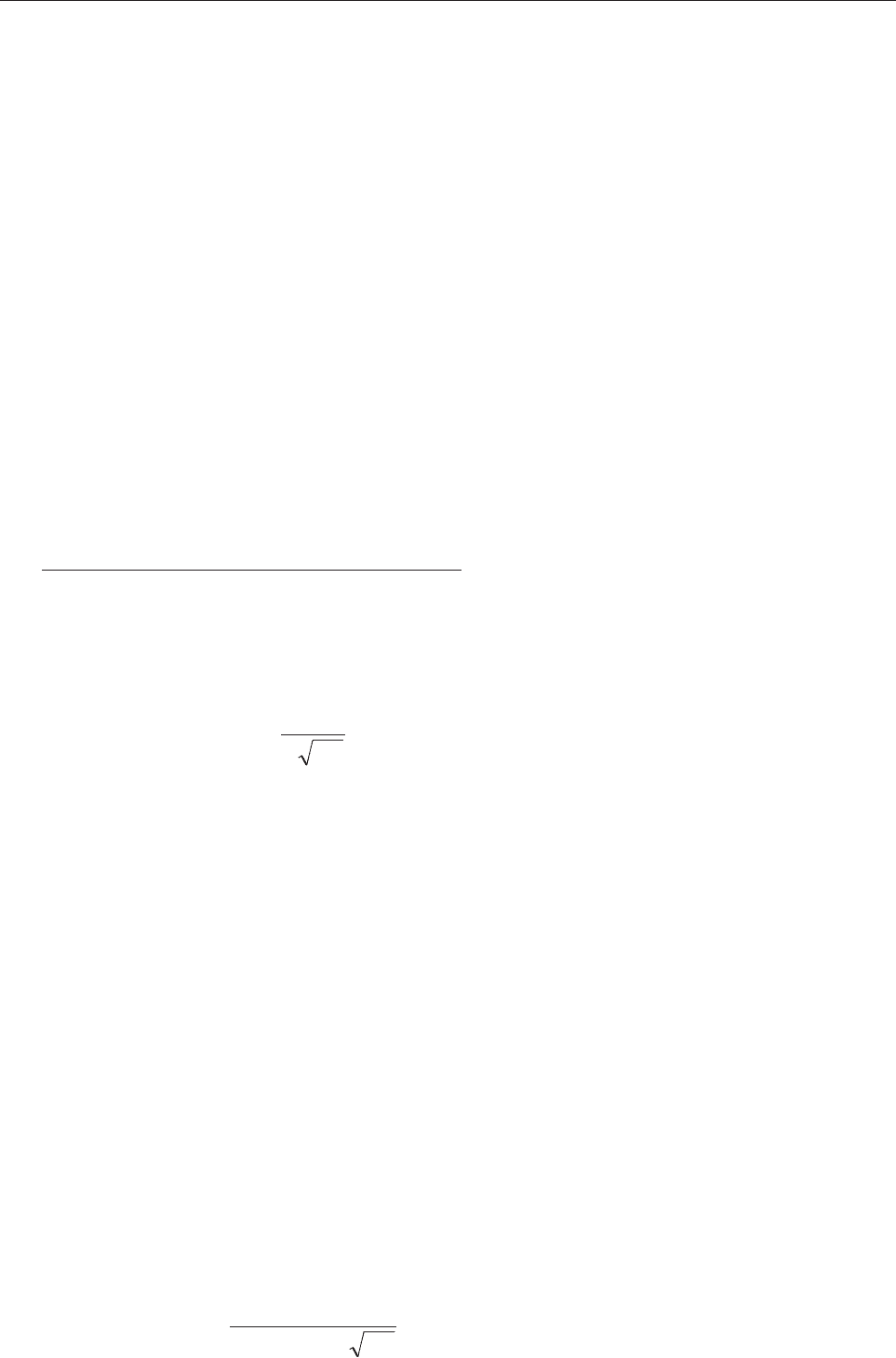
Çíà÷åíèå ôóíêöèè ðàñïðåäåëåíèÿ îïðåäåëÿåòñÿ ôîðìóëîé:
Ft u Qt u t T() , ( ) (); ( )/=+ = =−05 Φσ
. (4.3.21)
Âåðîÿòíîñòü îòñóòñòâèÿ îòêàçà çà âðåìÿ t:
[]
Pt Qt u Ôu() () , ( ) , ( )=− =− + = −1 1 05 05Φ
. (4.3.22)
Çíà÷åíèÿ F(t) òàáóëèðîâàíû (ïðèëîæåíèå 3).
Ãðàôèê l(t) ïîêàçàí íà ðèñ. 4.3.3, ã. Èíòåíñèâíîñòü îòêàçîâ ìîíîòîííî
âîçðàñòàåò è ïîñëå T íà÷èíàåò ïðèáëèæàòüñÿ ê àñèìïòîòå:
ytT=−()/σ
. (4.3.23)
Ìîíîòîííîå âîçðàñòàíèå èíòåíñèâíîñòè îòêàçîâ ñ òå÷åíèåì âðåìåíè —
õàðàêòåðíûé ïðèçíàê íîðìàëüíîãî ðàñïðåäåëåíèÿ. Íîðìàëüíîå ðàñïðåäå
-
ëåíèå ñóùåñòâåííî îòëè÷àåòñÿ îò ýêñïîíåíöèàëüíîãî. Íà÷àëîì îòñ÷åòà âðå
-
ìåíè t â (4.3.20) ñëóæèò íà÷àëî ýêñïëóàòàöèè îáúåêòà, ò. å. ìîìåíò, êîãäà
íà÷èíàåòñÿ ïðîöåññ èçíîñà è ñòàðåíèÿ, à íà÷àëîì îòñ÷åòà â (4.3.4) — ìîìåíò
âðåìåíè, êîãäà óñòàíîâëåíî, ÷òî èçäåëèå èñïðàâíî (ýòîò ìîìåíò ìîæåò áûòü
ðàñïîëîæåí â ëþáîé òî÷êå íà îñè âðåìåíè).
Óñå÷åííîå íîðìàëüíîå ðàñïðåäåëåíèå
(ðèñ. 4.3.3, ä). Òàê êàê ïðè íîðìàëü-
íîì ðàñïðåäåëåíèè ñëó÷àéíàÿ âåëè÷èíà ìîæåò ïðèíèìàòü ëþáûå çíà÷åíèÿ
îò
−∞
äî
+∞
, à âðåìÿ áåçîòêàçíîé ðàáîòû ìîæåò áûòü òîëüêî ïîëîæèòåëü-
íûì, ñëåäóåò ðàññìàòðèâàòü óñå÷åííîå íîðìàëüíîå ðàñïðåäåëåíèå ñ ïëîòíî-
ñòüþ âåðîÿòíîñòè îòêàçîâ:
()
ft t T() exp /=−−
⎡
⎣
⎢
⎤
⎦
⎥
1
2
2
1
2
2
σπ
σ
.
(4.3.24)
Íîðìèðóþùèé ìíîæèòåëü c îïðåäåëÿåòñÿ èç âûðàæåíèÿ:
cftdt() =
∞
∫
1
0
(4.3.25)
è ðàâåí:
()
[]
cFT T==+1105
101
/( /) /, /σσΦ
, (4.3.26)
ãäå:
()
FT x dx
T
(/) / exp /
/
1
2
12 2
1
σπ
σ
=−
−∞
∫
—
(4.3.27)
òàáóëèðîâàííàÿ (ïðèëîæåíèå 4) èíòåãðàëüíàÿ ôóíêöèÿ íîðìàëüíîãî ðàñ
-
ïðåäåëåíèÿ;
()
Φ
01
2
12 2
1
(/) / /
/
Txdx
T
σπ
σ
=−
−∞
∫
—
(4.3.28)
íîðìèðîâàííàÿ ôóíêöèÿ Ëàïëàñà.
Òîãäà (4.3.24) çàïèøåòñÿ ñëåäóþùèì îáðàçîì:
()
ft
FT
tT()
(/)
exp /=−−
⎡
⎣
⎢
⎤
⎦
⎥
1
2
2
1
1
2
2
σσ π
σ
.
(4.3.29)
149
à ËÀÂÀ 4

Ñðåäíÿÿ íàðàáîòêà äî îòêàçà â óñå÷åííîì ðàñïðåäåëåíèè è ïàðàìåòð T
1
íåóñå÷åííîãî íîðìàëüíîãî ðàñïðåäåëåíèÿ ñâÿçàíû çàâèñèìîñòüþ:
()
TT ft
FT
T=+ = −
1
1
1
2
2
2
2()
(/)
exp /
σ
πσ
σ
.
(4.3.30)
Ïðè
T / σ≥2
, ÷òî èìååò ìåñòî â àáñîëþòíîì áîëüøèíñòâå ñëó÷àåâ ïðè
îöåíêå íàäåæíîñòè óñòðîéñòâ ñ íîðìàëüíî ðàñïðåäåëåííûìè îòêàçàìè, êî
-
ýôôèöèåíò c ìàëî îòëè÷àåòñÿ îò åäèíèöû è óñå÷åííîå íîðìàëüíîå ðàñïðåäå
-
ëåíèå äîñòàòî÷íî òî÷íî àïïðîêñèìèðóåòñÿ îáû÷íûì íîðìàëüíûì çàêîíîì.
Âåðîÿòíîñòü áåçîòêàçíîé ðàáîòû îïðåäåëÿåòñÿ èç âûðàæåíèÿ:
()
[]
Pt
FT t
FT
()
/
(/)
=
−
1
1
σ
σ
.
(4.3.31)
Èíòåíñèâíîñòü îòêàçîâ íàõîäèòñÿ èç:
()
λ
σ
πσ
()
exp /
(( ) / )
t
tT
FT t
=
−−
⎡
⎣
⎢
⎤
⎦
⎥
−
1
2
2
1
2
2
.
(4.3.32)
Ðàñïðåäåëåíèå Ðýëåÿ
(ðèñ. 4.3.3, å) — íåïðåðûâíîå ðàñïðåäåëåíèå âåðîÿò-
íîñòåé ñ ïëîòíîñòüþ:
px x x() / exp( / )=−σσ
222
2
ïðè
x > 0
;
px()= 0
ïðè
x ≤ 0
,
çàâèñÿùåé îò ìàñøòàáíîãî ïàðàìåòðà
σ>0
. Ðàñïðåäåëåíèå èìååò ïîëîæèòå-
ëüíóþ àñèììåòðèþ, åãî åäèíñòâåííàÿ ìîäà íàõîäèòñÿ â òî÷êå
x =σ
. Âñå ìî-
ìåíòû ðàñïðåäåëåíèÿ Ðýëåÿ êîíå÷íû.
Òàêæå êàê è ðàñïðåäåëåíèå Âåéáóëëà èëè γ-ðàñïðåäåëåíèå, ðàñïðåäåëå-
íèå Ðýëåÿ ïðèãîäíî äëÿ îïèñàíèÿ ïîâåäåíèÿ èçíàøèâàþùèõñÿ èëè ñòàðåþ-
ùèõ èçäåëèé.
×àñòîòà îòêàçîâ (ôóíêöèÿ ïëîòíîñòè ðàñïðåäåëåíèÿ âåðîÿòíîñòè îòêà-
çîâ) îïðåäåëÿåòñÿ:
ft t t() / exp( / )=−σσ
222
2
. (4.3.33)
Âåðîÿòíîñòü áåçîòêàçíîé ðàáîòû âû÷èñëÿåòñÿ èç âûðàæåíèÿ:
Pt t() exp( / )=−
22
2σ
. (4.3.34)
Èíòåíñèâíîñòü îòêàçîâ íàõîäèòñÿ èç:
λσ() /tt=
2
. (4.3.35)
Ñðåäíÿÿ íàðàáîòêà äî ïåðâîãî îòêàçà ñîñòàâèò:
T =⋅πσ/2
.
(4.3.36)
150
à ËÀÂÀ 4
