Афанасьев А.А. Математические основы теории систем управления

Подождите немного. Документ загружается.

40 41

)()(

),(),(

AYAX

вQвQ

вв





(12.13)





 





 

вQ

arctg









(12.14)

Уравнение (12.13) при заданных значениях амплитуды

, и

частоты



внешнего воздействия содержит только одно неизве-

стное – амплитуду

вынужденных колебаний:

),(

BAA





. (12.15)

При известной зависимости (12.15) фазовый сдвиг



легкоо

вычисляется по формуле (12.14). Уравнение (12.13) для определе-

ния амплитуды может быть до-

статочно сложным. Однако при

любой его сложности возможен

такой простой способ его реше-

ния. Задаемся рядом значений



по формуле (12.13) вы-

числяем амплитуду внешнего

воздействия

, т.е. находим се-

мейство зависимостей по пара-

метру



),,(

ABB





(12.16)

из которой несложно получить

зависимость (12.15), показанную

на рис.12.5.

12.3. СКАЧКООБРАЗНЫЙ РЕЗОНАНС ПРИ

ВЫНУЖДЕННЫХ КОЛЕБАНИЯХ

Зависимость амплитуды колебаний

от амплитуды внеш-

него воздействия

),( BAA



const





(12.17)

может, в общем случае, иметь неоднозначный характер (рис.12.6).

const





Рис.12.5.Семейство зависимостей

амплитуды вынужденных

колебаний от амплитуды

внешнего гармонического

воздействия по параметру



ние режима связано с тем, что

при

пор

BВ



внешнее периоди-

ческое воздействие частоты







подавляет ранее суще-

ствовавшее автоколебание час-

тоты

 - имеет место срыв ав-

токолебаний.

При достаточно высокой

частоте



амплитуда вынуж-

денных колебаний

может

быть достаточно малой, следо-

вательно будет малой и ампли-

туда колебания ошибки

. По-

этому часто при



ре-

жим захватывания использу-

ют для подавления автоколебаний.

При

пор

BВ



в системе возникают сложные колебания (ре-

жим биений) на частотах внешнего воздействия



и собствен-

ной

 - имеем неодночастотные колебания.

АНАЛИТИЧЕСКИЙ МЕТОД

Уравнение гармонического баланса (12.8), с учетом выраже-

ния (11.14) можно представить в таком виде:

)(

)()()(









вв

BeA

AKjRjQ



(12.10)

Выделим вещественные и мнимые части в числителе и зна-

менателе. Записанного выражения

















,,,)(

вв

AjYAXАKjRjQ 



(12.11)

).()()(

ввQb

jYXjQ











(12.12)

Обратим внимание, что составляющие

),(



),(



были уже введены ранее (см. формулу (11.19)).

С учетом введенных обозначений можем получить уравне-

ние для модулей и фраз левых и правых частей выражения (12.10)

пор



Область

захватывания

Сложный

процесс

Сложный

процесс

Рис.12.4.Пороговое значение

амплитуды внешнего

гармонического сигнала,

при котором возможно

существование вынужденных

колебаний на частоте



42 43

ГЛАВА ТРИНАДЦАТАЯ

УПРАВЛЕНИЕ И УСТОЙЧИВОСТЬ ПРИ НАЛИЧИИ

В СИСТЕМЕ ВЫСОКОЧАСТОТНЫХ КОЛЕБАНИЙ

Эффективным, способом подавления автоколебаний являет-

ся наложение на нелинейное звено вынужденных колебаний дос-

таточно высокой частоты по сравнению с частотой автоколеба-

ний. Такой метод подавления автоколебаний называют вибраци-

онной линеаризацией нелинейной характеристики [11].

Высокочастотные колебания в системе автоматического уп-

равления могут появиться также как внешняя вибрационная поме-

ха, например, из-за вибрации корпуса летательного аппарата [2].

13.1.ПРОЦЕССЫ УПРАВЛЕНИЯ ПРИ НАЛИЧИИ

ВНЕШНЕГО ПЕРИОДИЧЕСКОГО ВОЗДЕЙСТВИЯ

13.1.1.ТЕОРЕТИЧЕСКИЕ ОСНОВЫ

Пусть ко входу нелинейной системы (рис.10.1) приложены два

воздействия:





tBtg





sin





(13.1)

причем





- медленно меняющееся внешнее воздействие по срав-

нению с первым периодическим воздействием





. Характер из-

менений этих воздействий таков, что за период первого воздей-

ствия

вв







второе воздействие остается практически без

изменения. Медленное воздействие





может рассматриваться

как управляющее.

Сигнал ошибки системы ищем в виде:

),()()(

txtxtx 

(13.2)

где





 tAtx

sin)(

– (13.3)

– быстрая (колебательная) составляющая (ее амплитуда

и фаза



, в общем случае, допускают медленное изменение);

)(

- мед-

ленная составляющая ошибки, обусловленная сигналом управле-

ния





В этом случае какому-то

одному уровню внешнего сиг-

нала, может соответствовать

несколько значений амплитуд

вынужденных колебаний.

При вынужденных колеба-

ниях кривой 2 на рис.12.7 будет

отвечать три точки пересече-

ния кривой

),(



с окруж-

ностью радиуса

, величина

которого принадлежит интерва-

лу (рис.12.7):



(12.18)

Из кривой 2 рис 12.6 сле-

дует, что при увеличении

на-

блюдаем плавный рост

, но

при значении





происхо-

дит скачкообразный рост амп-

литуды вынужденных колебаний

. При последующем умень-

шении амплитуды вешнего воз-

действия

имеет место при





снижение скачком амп-

литуды

Условием существования

скачкообразного резонанса на

фиксированной частоте вынужденных колебаний является на-

личие у зависимости (12.7) участка (12.18), на котором спра-

ведливо неравенство:

.0













 const

(12.19)



Рис.12.6.Однозначный (кривая 1) и

неоднозначный (кривая 2)

характер зависимости

амплиттуды колебаний

от амплитуды внешнего

воздействия при

const



),(

AZ 

Рис.12.7.К обоснованию

скачкообразного резонанса

44 45

Гармоническая линеариза-

ция позволяет аппроксимировать

нелинейную зависимость





)()( txty





следующим выра-

жением:

)cossin(),()(





ΑxΑty

, (13.9)

Которое можно представить и в другой форме





),(sin),(),()(

0000

xΑxΑΑxΑty 



, (13.10)

где









),(),(),( xΑxΑxΑ

СS

ГГГ



, (13.11)

),(

xΑ

arctg





. (13.12)

При символической форме записи выражений (13.1), (13.3),

(13.10) имеем:

Βetg



)(



)(







Αetx



, (13.13)

Ф(х)

 







)( t

Ф

Рис.13.2.Прохождение сигнала

через нелинейное звено с идеальной

релейной характеристикой

При гармоничесеой линеаризации нелинейного звена медлен-

ная составляющая входного сигнала может считаться неизмен-

ной на временном интервале равном периоду быстрой составляю-

щей (рис.13.1, 13,2).

В этом случае имеем :





,sin)(











tAxtx

(13.4)

где

- смещение периодическо-

го сигнала.

Временная периодическая зависимость ),( t





будет содер-

жать кроме первой гармоники и постоянную составляющую

 











sinsin

),( dAx

xAK

(13.5)

 

,cossin

),(









 dAx

xAK

(13.6)

 

,sin

),(

000











dAxxA ФФ

(13.7)

где











. (13.8)

Ф(х)



 







)( t

Ф

Рис.13.1.Прохождение сигнала

через нелинейное звено

типа “ограничение

46 47

В результате решения (13.21) определится зависимость

constconst







ΒxΑΑ

,),(

. (13.22)

Подставляя это решение в функцию

),(

xΑ



получим нели-

нейную зависимость

)),(()(

00000

xxΑx 

. (13.23)

Можно показать, что нелинейная зависимость (13.23) имеет

вид плавной кривой, проходящей через начало координат, при лю-

бых нелинейностях )(xy





, в том числе релейных и гистерезис-

ных (рис.13.3).

Применяя дифференциаль-

ную линеаризацию зависимости

(13.23) в начале координат, по-

лучим

000

xK

, (13.24)

где







Таким образом, для нахож-

дения коэффициента

требует-

ся иметь решение уравнения

(13.21) с целью получения нелинейной зависимости (13.23). Одна-

ко , как легко показать, дифференциальная линеаризация (13.24)

может быть получена и без нахождения решения уравнения (13.21),

так как

),(













xΑ

. (13.25)

Действительно, применительно к правой части выражения

(13.23) имеем

000

)),((































dΑ

xxΑ

. (13.26)

)(

x

ktg



Рис.13.3.Линеаризация нелинейной

зависимости

)(),(),()(

000

txxΑxΑty







, (13.14)

где

),(),(),(),(

),(

xΑjxΑexΑxΑ

xΑj

ГГГГ







. (13.15)

Причем очевидно:













).,(sin),(),(

),,(cos),(),(

000

xΑxΑxΑ

ГГ

(13.16)

Обращаясь к интегральному уравнению вынужденного дви-

жения (10.33) можем, с учетом формул (13.2), (13.13), (13.14) на-

писать



.)(),(),()()()()(

00010









dtxxΑΚxΑktgtgtxx





(13.17)

Это уравнение разобьем на два, относящихся соответствен-

но к медленным и быстрым процессам







000

),()()( dxΑktgx

, (13.18)







)(*)(),()()(* dtxkxΑΚtgtх





, (13.19)

Последнее уравнение можно, по аналогии с уравнением (12.4),

привести к виду

)(

),()(1

)(*

xΑjW

tх





 . (13.20)

С учетом формул (13.1), (13.13) из уравнения (13.20) следует









ΒexΑΚjW ),()(1



. (13.21)

Задаваясь различными значениями

это уравнение, как и

уравнение (12.8), можно решить графическим или аналитическим

методами ( см. раздел 12.2) при известных значениях амплитуды

и частоты



внешнего периодического воздействия.

48 49

где





)()( tgLpG







)()( tkLpW



- передаточная функция линей-

ной части системы.

Коэффициент

называют, коэффициентом усиления не-

линейности в процессе управления при наложении быстрого

периодического процесса или коэффициентом вибрационной

линеаризации нелинейности для процесса управления.

Коэффициент

, как следует из формулы (13.25), определя-

ется равенством

),(









xΑ

, (13.31)

в котором нелинейность

),(

xΑ



задается формулой (13.7). Из

этой формулы и выражения (13.31) следует, что коэффициент

является функцией только амплитуды

симметричных (



)

вынужденных колебаний ошибки

)(

00 C

ΑΚΚ



. (13.32)

Для рассмотренной выше характеристики с насыщением

(рис.13.1) получим

)(arcsin

bΑ









. (13.33)

Для аналогичной характеристики, но с зоной нечувствитель-

ности (рис.10.12) справедливо















Κ arcsin(arcsin

. (13.34)

Коэффициенты усиления нелинейности типа релейных харак-

теристик соотвественно с зоной нечувствительности (рис.10.16) и

общего вида (с гистерезисными петлями рис.10.18) вычисляют-

ся по формулам

aΑ





, (13.35)

Согласно формуле (13.7) получим

0sin

sin



































xΑ

Αx

, (13.27)

поскольку функция



















является четной, а интеграл (13.27)

от произведения четной функции на нечетную равен нулю.Поэто-

му из формулы (13.26) следует равенство (13.25).Это значит, что

для определения коэффициента дифференциальной линеаризации

нет нужды находить решение (13.22) и вычислять нелинейную

зависимость (13.23). Достаточно взять частную производную по

в точке



от известной для каждой нелинейности зависи-

мости (13.7).

С учетом полученной зависимости (13.24) уравнение (13.18)

для медленного процесса управления получит вид (при отсутствии

"замораживания" времени t).







000

)()()()( dtxkΚtgtx

. (13.28)

Видим, что это уравнение, как уравнение (13.19) для вынуж-

денного периодического процесса, является линейным.

При приложении управляющего воздествия

)(tg

в момент вре-

мени 0



t к системе, находящейся в покое, (а не в момент вре-

мени





для вынужденного процесса) уравнение (13.28), в со-

ответствии с формулой (9.5), запишится так





dxtkKtgtx

000

)()()()(

. (13.29)

При переходе от временных зависимостей к изображениям

по Лапласу получим из формулы (13.29) с учетом зависимости

(9.4):

)(

)(1

)(

pWΚ





, (13.30)

50 51

13.1.2.ПРАКТИЧЕСКИЕ ПРИМЕРЫ.

ПРИМЕР 13.1

Вибрационное сглаживание и вибрационная линеаризация

нелинейности при помощи вынужденных вибраций

Нелинейная зависимость )(xy





, допускающая скачки и ги-

стерезисные петли, по отношению к медленному сигналу управ-

ления

)(

трансформируется в монотонную однозначную нели-

нейную зависимость





x

, проходящую через начало коорди-

нат (рис.13.3).

Переход от функции







, у которой аргумент



 xxx

со-

держит быструю и медленную составляющие, к функции





x

зависящей, только от медленной составляющей управления, на-

зывается вибрационным сглаживанием нелинейности для процес-

са управления.

Слабо нелинейная зависимость





x

в результате диффе-

ренциальной линеаризации в начале координат может заменена ли-

нейной функций.

000

xΚ

. (13.39)

Переход от сглаженной (вторичной) нелинейности





x

линейной зависимости (13.39) называют вибрационной линеариза-

цией нелинейности.

Практическая реализация вибрационного сглаживания пока-

зана на рис.13.5.

Непосредственно на вход нелинейного звена (например, ре-

лейного элемента) прикладывается гармоническое (вибрационное)

воздействие

tΒtg





sin)(

с частотой, превышающей полосу про-

Рис.13.5.Практическая реализация вибрационного сглаживания

tΒtg

 sin)(

)(tg n

Линейное

звено 1

Линейное

звено 2

Нелиней-

ное

звено Ф(x)

Осталь-

ная часть

системы























2222

)(

mbΑbΑ

. (13.36)

Амплитуда симметричных колебаний

, как показано в пре-

дыдущем параграфе, может определяться графически или анали-

тически. Она зависит от амплитуды и частоты внешнего воздей-

ствия, а также от параметров





ΤΚ ,

линейной части системы

(см. (13.21))

),(

вCC

ΒΑΑ





. (13.37)

Качественный вид зависимости (13.37) показан на рис.12.5.

Амплитуда

может вычисляться также в функции какого-либо

параметра системы

ΤΚ ,

(рис.12.2,в).

),(

iiCC

ΤΚΑΑ



const



const





. (13.38)

Графики на рис.13.4 а,б построены соответственно по форму-

лам (13.33),(13.36).

0 0



а) б)

Рис.13.4.Графики построены соответственно по формулам

(13.33)–а),(13.36)–б).

52 53

рис. 13.1, обеспечивает ограничение скорости привода) имеем

сигнал вида (13.2), состоящий из медленной (управляющей) и бы-

строй (вибрационной) составляющих.

Процесс управления описывается линейным операторным

выражением (13.30), характеристическое уравнение которого имеет

вид

0)()(





pRΚpQ

, (13.43)

где

- коэффициент усиления нелинейности, зависящий от амп-

литуды и частоты внешнего вибрационного воздействия

tΒtg





sin)(

. (13.44)

Следовательно, параметры вибрационной помехи (13.44) че-

рез коэффициент оказывают влияние на характер распределения

на комплексной плоскости корней характеристического уравнения

(13.43), т.е. от этих помех будет зависеть качество процесса уп-

равления и устойчивость системы.

Обычно с ростом амплитуды

вибрационной помехи систе-

ма приближается к границе устойчивости. Предельное значение

амплитуды

, до которого система остается еще устойчивой, на-

зывается границей устойчивости системы к вибрационным поме-

хам [2].

13.2.ПРОЦЕССЫ УПРАВЛЕНИЯ В

АВТОКОЛЕБАТЕЛЬНЫХ СИСТЕМАХ

Среди систем автоматического управления встречаются ав-

токолебательные системы, у которых частота автоколебаний вы-

бирается много больше спектра возможных частот процесса уп-

равления.

Поэтому переменная на входе нелинейного звена может быть

представлена двумя составляющими

)()()(

txtxtx 

, (13.45)

где

)(

- медленная составляющая по сравнению с автоколеба-

тельной (быстрой)

)(tx



, обусловленная управляющим воздействи-

ем (см.рис.10.1);

пускания последующего линейного звена 2. Поэтому вынужден-

ные колебания отсутствуют на выходе этого звена.

Сигнал на входе нелинейного звена содержит быструю (

) и

медленную (

) составляющую

xxx 

где

310

xxx





ttgx

 sin)(

В этом случае, как следует из формулы (13.3),







AB . (13.40)

Наличие внешнего периодического сигнала позволяет ликви-

дировать гистерезисную петлю и зону нечувствительности реле

для медленного (управляющего) сигнала

)(tg

Для этого сигнала нелинейное звено будет представлено только

коэффициентом усиления

. Например, для релейного элементаа

с зоной нечувствительности (рис. 10.16,а) коэффициент

мож-

но определить по формуле (13.35) с учетом равенства (13.40)

aΒ

Κ 



 ,

. (13.41)

Амплитуда

вибрационного воздействия должна обеспе-

чивать срабатывание элемента при максимальном значении сиг-

нала управления:

max

xaΒ 

, (13.42)

где

x - максимальное значение медленного сигнала на входе не-

линейности, до которого требуется обеспечить линейность релей-

ного элемента.

ПРИМЕР 13.2

Устойчивость к вибрационным помехам нелинейной системы

В летательных аппаратах высокочастотная вибрация корпу-

са может передаваться оси гироскопа, вызывая ее быстрое дви-

жение относительно пространственных осей аппарата. Управляю-

щее воздействие на руле аппарата вызывает медленное движение

оси гироскопа относительно пространственных осей аппарата. Та-

ким образом, на выходе нелинейности в цепи управления электро-

привода руля (эта нелинейность типа “насыщение”, показанная на

54 55

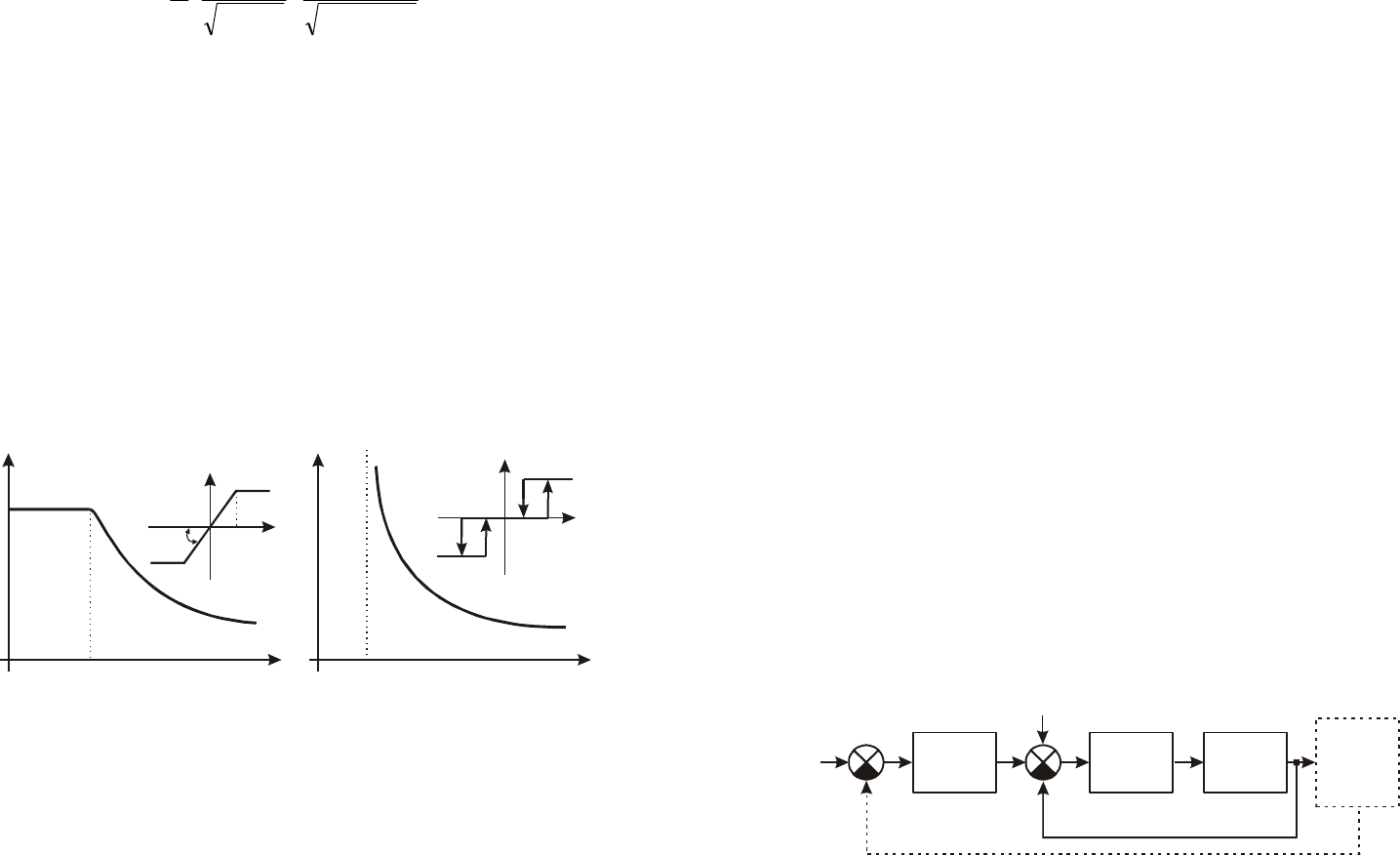
Рис.13.6.Автоколебательный контур с нелинейным звеном, линейной

частью и цепью обратной связи

Линейная

часть

Нелинейное

звено

Линейная

обратная

связь

Параметры этого контура выбираются такими, чтобы,

во-первых, частота автоколебаний была достаточно высо-

кой по сравнению с частотой сигнала управления, во-вторых,

амплитуда автоколебаний

была не меньше возможных

)(

на входе нелинейного звена





max

xΑ 

2. При наличии вибрационного сглаживания нелинейнос-

ти процессы управления рассчитываются при замене нели-

нейного звена коэффициентом усиления

3. Зона нечувствительности и петли гистерезиса устра-

няются.

4. Коэффициент усиления нелинейности

является фун-

кцией амплитуды

симметричных автоколебаний быст-

рой составляющей на входе нелинейного звена. Поэтому из-

менение

оказывает влияние на качество управления и ус-

тойчивость системы в целом.

;sin)(

 Αtx











. (13.46)

При отсутствии внешнего периодического воздействия

)0)((



из уравнения (13.20) для быстрой составляющей

)(tx



следует равенство

0),()(1

 xΑΚjW



. (13.47)

Медленная составляющая удовлетворяет уравнению (13.30).

Из выражения (13.47), задаваясь произвольным значением

можем, как показано в параграфе 11.2, найти амплитуду и частоту

автоколебательной составляющей, как функции смещения

),(

xΑΑ



)(







. (13.48)

Если нелинейность однозначная (без гистерезисных петель),

то коэффициент гармонической линеаризации нелинейности

),(

xΑΚ



является вещественным и, как видно из рис. 11.2, не

оказывает влияние на частоту автоколебаний



. Последняя бу-

дет определяться свойствами линейной части системы и не будет

зависеть от составляющей управления

Коэффициент усиления нелинейности

в уравнении управ-

ления (13.30) зависит от амплитуды симметричных автоколеба-

ний, т.е. колебаний при



. Его значение можно найти по фор-

мулам (13.33) - (13.36).

Особенности управления

1. За счет автоколебательных вибраций любая нелиней-

ная характеристика, в том числе скачкообразная и гистере-

зисная, трансформируется в зависимость

)(

000

x

, кото-

рая близка к линейной зависимости

000

xΚ

где









- коэффициент усиления нелинейного звена.

Это вибрационное сглаживание нелинейности реализуется

путем создания автоколебательного контура с нелинейным зве-

ном, линейной частью и цепью обратной связи (рис.13.6).

56 57

В первом приближении это решение может соответствовать

и системе высокого порядка, если корни

 j

2,1

(14.2)

выбраны ближайшими к мнимой оси.

Для нелинейной системы аналогичное приближение можно

представить в виде





sinax , (14.3)

Причем величины





связаны дифференциальными

уравнениями

 a





, (14.4)

из которых при const





const





следуют выражения (14.1).

Дифференцируя по времени (14.3) с учетом (14.4), получим













sincos aapx . (14.5)

Из формул (14.3), (14.5) следует

sin

;





cos

. (14.6)

При гармонической линеаризации нелинейности )(xy





име-

ем из (10.10) и (14.6)

ΚΚΚΚay

СSCS

)()cossin(







ГГГГ

, (14.7)

В этой формуле множитель в круглой скобке перед перемен-

ной

можно рассматривать как передаточную функцию гармо-

нически линеаризованного нелинейного звена

,)()(),(









 p

aΚaΚa

СS

ГГГ

(14.8)

где коэффициенты гармонической линеаризации

)(aΚ

определяются как функции амплитуды по известным формулам

(см. параграф 10.2.3).

Принимая во внимание характеристическое уравнение ли-

неаризованной замкнутой системы (11.16), получим

ГЛАВА ЧЕТЫРНАДЦАТАЯ

ОЦЕНКА КАЧЕСТВА КОЛЕБАТЕЛЬНЫХ ПЕРЕХОДНЫХ

ПРОЦЕССОВ В НЕЛИНЕЙНЫХ СИСТЕМАХ

Будем рассматривать собственные колебания в нелинейной

системе, ( 0)(



tg ). Эти колебания могут быть затухающими или

расходящимися (рис.14.1). У первых амплитуда уменьшается до

нуля или до амплитуды автоколебаний, у вторых амплитуда возра-

стает до амплитуды автоколебаний или неограничена у неустой-

чивой системы.

Частота колебаний в переходном процессе также испытыва-

ет изменения.

Необходимо рассчитать быстроту изменения амплитуды и

частоты колебаний.

14.1.МЕТОД ИССЛЕДОВАНИЯ КОЛЕБАТЕЛЬНЫХ

ПЕРЕХОДНЫХ ПРОЦЕССОВ В ПЕРВОМ

ПРИБЛИЖЕНИИ

Для линейной системы второго порядка (с двумя комплекс-

но-сопряженными корнями) колебательный переходный процесс

описывается уравнением

,sin)( ttax





,)(

eatа





(14.1)

где частота



и показатель затухания



величины неизменные.

а) б)

)(

)(tx

)(ta

)(

0 0

Рис. 14.1.Затухающие колебания

58 59

Эта информация фиксируется в так называемых диаграммах

качества, которые представляют собой семейства кривых

(рис.14.2)

),(kaa



const





; (14.13)

),(kaa



const





. (14.14)

Для линейных систем эти кривые имели бы вид вертикаль-

ных прямых, так как в этом случае коэффициент затухания и час-

тота не зависят от амплитуды колебаний (они будут зависеть от

значения параметра k ).

Кривая 0





соответствует незатухающим автоколебаниям

с постоянной амплитудой (например,



для точки C ). Этаа

линия выражает зависимость амплитуды автоколебаний от пара-

метра k .

0const











0const







Область устойчивого

равновесия при



Область автоколебаний

Линии

const









L D

Рис.14.2. Диаграммы качества

0)(),()( 





 pRa

ΚpQ

. (14.9)

Из уравнения (14.8) найдем пару комплексно-сопряженных

корней (именно им соответствует колебательный переходный про-

цесс), ближайших к мнимой оси. Для чего выполним в (14.8) по-

становку









jp .

Будем иметь





0)()()()(  jRajΚaΚjQ

ГГ

. (14.10)

Полученное комплексное уравнение содержит три неизвест-

ных величины:





. Из него можно найти две величины как

функции третьей

),(a



)(a



. (14.11)1)

Зависимости (14.11) позволяют с помощью уравнений (14.4)

рассчитать колебательный процесс (14.3) для переменной )(tx .

Действительно, интегрируя первое дифференциальное урав-

нение (14.4) после подстановки в него известной функции )(a



получим зависимость амплитуды

от времени

)(taa



Интегрируя второе дифференциальное уравнение (14.4) с под-

становкой в него функций

)(a



и )(ta , находим

)(t







В результате из (14.3) получаем решение

)(sin)( ttax





. (14.12)

14.2.ДИАГРАММЫ КАЧЕСТВА ПЕРЕХОДНЫХ

ПРОЦЕССОВ

Для оценки качества системы нахождение решения (14.12)

обычно не требуется. Достаточно определить зависимости пока-

зателей





от амплитуды и от какого-либо параметра k

линейной части системы.